计量经济学-6自相关

第六章课后答案6.1（１）收入—消费模型为Se = (2.5043) (0.0075)t = (-3.7650) (125.3411)R2 = 0.9978，F = 15710.39，d f = 34，DW = 0.5234（２）对样本量为36、一个解释变量的模型、5%显著水平，查DW统计表可知，d L=1.411，d U= 1.525，模型中DW<d L，显然消费模型中有自相关。

（３）采用广义差分法查5%显著水平的DW统计表可知d L = 1.402，d U = 1.519，模型中DW= 2.0972>d U，说明广义差分模型中已无自相关。

同时，判定系数R2、t、F统计量均达到理想水平。

由差分方程式可以得出：所以最终的消费模型为：6.2（1）给定n=16, ,在的显著水平下，查DW统计表可知，。

模型中，所以可以判断模型中存在正自相关。

给定n=16, ,在的显著水平下，查DW统计表可知，。

模型中，所以可以判断模型中不存在自相关。

（2）自相关可能由于模型6.1的误设，因为它排除了趋势的平方项。

（3）虚假自相关是由于模型的误设造成的，因此就要求对可能的函数形式有先验知识。

真正的自相关是可以通过广义差分法等方法来修正。

6.3（１）收入—消费模型为（２）DW＝0.575，取，查DW上下界，说明误差项存在正自相关。

（３）采用广义差分法使用普通最小二乘法估计的估计值，得DW=1.830，已知，模型中因此，在广义差分模型中已无自相关。

由差分方程式可以得出：因此，修正后的回归模型应为6.4（1）回归结果如下：（2）模型检验：从回归结果可以看出，参数均显著，模型拟和较好。

异方差的检验：通过white检验可以得知模型不存在异方差。

DW检验：给定n=25, ,在的显著水平下，查DW统计表可知，。

模型中，所以可以判断模型中存在正自相关。

（3）采用广义差分法修正模型中存在的自相关问题：给定n=24，,在的显著水平下，查DW统计表可知，。

经济计量学之自相关引言经济计量学是以数理统计方法为基础，应用于经济现象的研究和分析的一门学科。

自相关是经济计量学中的一个重要概念。

自相关指的是观测序列中不同时刻之间的相关性。

在经济学中，自相关经常应用于时间序列的分析，用于研究经济现象在时间上的相关性与趋势。

自相关的基本概念自相关是指同一时间序列的不同观测值之间的相关性。

一般情况下，时间序列的自相关用自相关系数（autocorrelation coefficient）来衡量。

自相关系数的取值范围为-1到1之间，取决于观测值之间的相关性。

自相关系数的计算公式如下所示：formulaformula其中，Cov表示时间点t和时间点t-k之间的协方差，sigma和sigma分别表示时间点t和时间点t-k的标准差。

当自相关系数接近于1时，表示观测序列在不同时间点上具有很强的相关性，即存在显著的长期相关性。

当自相关系数接近于-1时，表示观测序列在不同时间点上呈现出负相关性。

当自相关系数接近于0时，表示观测序列在不同时间点上呈现出随机性，不存在相关性。

自相关的应用自相关在经济学中有广泛的应用。

下面列举了几个常见的应用场景：1. 时间序列预测自相关分析可用于时间序列预测。

利用过去观测数据之间的自相关性，可以对未来的观测值进行预测。

通过分析自相关系数，可以确定合适的预测模型，如自回归移动平均模型（ARMA模型）或自回归积分滑动平均模型（ARIMA模型）。

2. 经济周期分析自相关分析可用于研究经济周期的波动特征。

经济周期是一种重要的经济现象，对宏观经济政策制定和企业经营决策具有重要意义。

通过对经济数据进行自相关分析，可以发现周期性的波动模式，从而对未来的经济变化进行预测和研究。

3. 时间序列平稳性检验自相关分析可用于检验时间序列的平稳性。

平稳性是时间序列分析的基本假设之一，意味着时间序列的均值和方差在不同时间段上保持不变。

通过计算自相关系数，可以评估时间序列的平稳性，并对序列进行必要的转换以满足平稳性的要求。

计量经济学第六章作业思考题：6.1 如何使用DW统计量来进行自相关检验？该检验方法的前提条件和局限性有哪些？答：（1）DW 检验是J.Durbin(杜宾)和G.S.Watson(沃特森)于1951年提出的一种适用于样本容量大于等于15的检验自相关的方法，许多计量经济学和统计学计算机软件都可以计算出DW 值。

给定显著水平α，依据样本容量n和解释变量个数k’（不包括常数项），查D.W.分布表可得临界值（d统计量的上界d U和下界d L），当0<DW<d L时，表明存在一阶正自相关，而且正自相关的程度随DW向0的靠近而增强。

当d L<DW<d U时，表明为不能确定是否存在自相关。

当d U<DW<4-d U时，表明不存在一阶自相关。

当4-d U<DW<4-d L时，表明不能确定是否存在自相关。

当4-d L<DW<4时，表明存在一阶负自相关，而且负自相关的程度随DW向4的靠近而增强。

（2）DW检验的前提条件：<1>解释变量是非随机的（因此与随机扰动项不相关）；<2>随机扰动项是一阶自回归形式，即u t=ρu t-1 +v t (v t满足古典假定)；<3>线性模型的解释变量中不包含滞后的被解释变量，如不应出现下列形式：Y t =β1 +β2 X t +β 3 Y t-1 +u t；<4>截距项不为零，即只适用于有常数项的回归模型；<5>数据序列无缺失项，样本比较大。

（3）DW检验的局限性：<1>DW检验有两个不能确定的区域，一旦DW值落在这两个区域，就无法判断。

这时，只有增大样本容量或选取其他方法；<2>DW统计量的上、下界表要求n≥15, 这是因为样本如果再小，利用残差就很难对自相关的存在性做出比较正确的诊断；<3> DW检验不适应随机误差项具有高阶序列相关的检验；<4> DW检验有运用的前提条件，只有符合这些条件DW检验才是有效的。

计量经济学第六章自相关自相关是计量经济学中一种重要的现象，它指的是一个变量与其自己在过去时间点上的相关性。

自相关在实证研究中十分常见，对经济学家来说，了解和掌握自相关性质是至关重要的。

1. 引言自相关作为计量经济学的一项基础概念，是经济学研究中不可或缺的一个重要方法。

自相关性的存在通常会引起回归结果的偏误，而忽略自相关性可能导致估计不准确的结果。

因此，探讨自相关性的性质和应对方法是计量经济学的重点之一。

2. 自相关的定义和表示自相关是指一个变量与其自身在过去时间点上的相关性。

假设我们有一个时间序列数据集，其中变量yt表示一个时间点上的观测值，t表示时间索引。

自相关系数可以通过计算观测值yt与其在过去某一时间点上的观测值yt-k（k为时间滞后期数）的相关性来得到。

数学上，自相关系数可以用公式表示为：ρ(k) = Cov(yt, yt-k) / (σ(yt) * σ(yt-k))其中，ρ(k)表示第k期的自相关系数，Cov表示协方差，σ表示标准差。

3. 自相关性的性质自相关性具有以下几个性质：3.1 一阶自相关性一阶自相关性是指变量值yt与前一期的观测值yt-1之间的相关性。

一阶自相关系数ρ(1)通常用来检验时间序列数据是否存在自相关性。

若ρ(1)大于零且显著，则表明存在正的一阶自相关性；若ρ(1)小于零且显著，则表明存在负的一阶自相关性。

3.2 高阶自相关性除了一阶自相关性，时间序列数据还可能存在高阶自相关性。

高阶自相关性是指变量值yt与过去第k期的观测值yt-k之间的相关性。

通过计算不同滞后期的自相关系数ρ(k)，可以了解数据在不同时间跨度上的自相关性情况。

3.3 异方差自相关性异方差自相关性是指时间序列数据中的方差不仅与自身相关，还与过去观测值的相关性有关。

异方差自相关性可能导致在回归分析中的标准误差失效，从而产生无效的回归结果。

因此，在处理存在异方差自相关性的数据时要采取合适的修正方法。

4. 自相关性的检验方法在实证研究中，经济学家通常使用多种方法来检验数据中的自相关性，常用的方法包括：4.1 Durbin-Watson检验Durbin-Watson检验是一种常用的检验自相关性的方法，其基本思想是通过检验误差项的相关性来判断自相关是否存在。

案例六：中国宏观消费分析（自相关，file:china ）按照我国现行国民经济核算体系，国内生产总值（按支出法计算）是由最终消费、资本形成总额和货物与服务的净出口之和三部分组成。

前两部分占绝大多数。

其中最终消费又分为居民消费和政府消费两类。

而居民消费又可分为农村居民消费和城镇居民消费。

在这种核算体系下，居民消费包括居民个人日常生活中衣、食、住、用等物质消费以及在文化生活服务性支出中属于物质产品的消费。

政府消费包括国家机关、国防、治安、文教、卫生、科研事业单位，经济建设部门的事业单位，人民团体等非生产机构使用的燃料、电力、办公用品、图书、设备等物质消费。

国内生产总值中最终消费与资本形成总额的比例关系，即旧核算体系下国民收入中消费与积累的比例关系是国民经济正常运行的最基本的比例关系。

如果这一比例关系发生严重失调，最终会成为制约经济正常运行的严重障碍。

下面分析中国的消费问题。

为消除物价变动因素以及异方差的影响，以下分析所用的数据均为不变价格数据（1952 = 1）以及分别取自然对数后的数据，见附表。

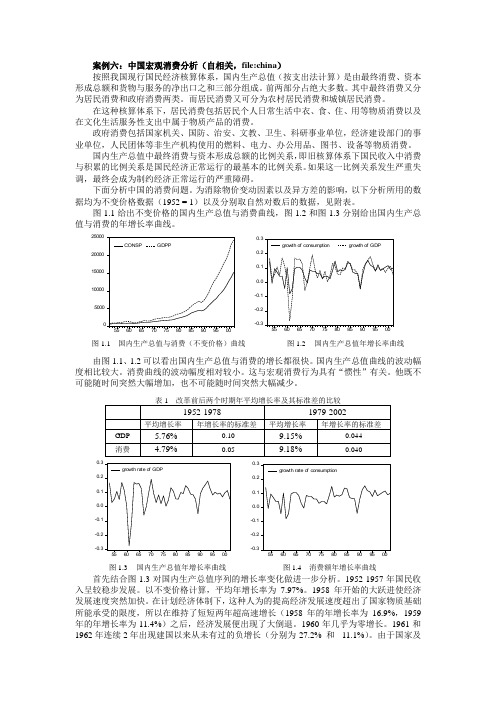
图1.1给出不变价格的国内生产总值与消费曲线，图1.2和图1.3分别给出国内生产总值与消费的年增长率曲线。

50001000015000200002500055606570758085909500CONSPGDPP-0.3-0.2-0.10.00.10.20.355606570758085909500growth of consumptiongrowth of GDP图1.1 国内生产总值与消费（不变价格）曲线 图1.2 国内生产总值年增长率曲线由图1.1、1.2可以看出国内生产总值与消费的增长都很快。

国内生产总值曲线的波动幅度相比较大。

消费曲线的波动幅度相对较小。

这与宏观消费行为具有“惯性”有关。

他既不可能随时间突然大幅增加，也不可能随时间突然大幅减少。

-0.3-0.2-0.10.00.10.20.355606570758085909500growth rate of GDP-0.3-0.2-0.10.00.10.20.355606570758085909500growth rate of consumption图1.3 国内生产总值年增长率曲线 图1.4 消费额年增长率曲线首先结合图1.3对国内生产总值序列的增长率变化做进一步分析。

第六章自相关实验报告一、研究目的对于广大的中国农村人口而言，其消费总量比重却不高。

农村居民的收入和消费是一个值得研究的问题。

消费模型是研究居民消费行为的常用工具。

通过中国农村居民消费模型的分析可判断农村居民的边际消费倾向，这是宏观经济分析的重要参数。

同时，农村居民消费模型也能用于农村居民消费水平的预测。

二、模型设定影响居民消费的因素很多，但由于受各种条件的限制，通常只引入居民收入一个变量做解释变量，即消费模型设定为：+β1X t+ U tY t=β参数说明：Y——农村居民人均消费支出 (单位：元)tX——农村居民人均纯收入（单位：元）tU t——随机误差项收集到数据如下（见表2-1）表2-1 1985-2011年农村居民人均收入和消费单位：元注：资料来源于《中国统计年鉴》1986-2012。

为了消除价格变动因素对农村居民收入和消费支出的影响，不宜直接采用现价人均收入和现价人均消费支出的数据，而需要用经消费价格进行调整后的1985年可比价格及人均纯收入和人均消费支出的数据做回归分析。

根据表2-1中调整后的1985年可比价格计的人均纯收入和人均消费支出的数据，使用普通最小二乘法估计消费模型得如下结果。

表2-2 最小二乘估计结果Dependent Variable: YMethod: Least SquaresDate: 12/04/13 Time: 20:00Sample: 1985 2011Included observations: 27Coefficient Std. Error t-Statistic Prob.C 45.40225 10.30225 4.407025 0.0002X 0.718526 0.012526 57.36069 0.0000R-squared 0.992459 Mean dependent var 580.5296 Adjusted R-squared 0.992157 S.D. dependent var 256.4506 S.E. of regression 22.71079 Akaike info criterion 9.154744 Sum squared resid 12894.50 Schwarz criterion 9.250732 Log likelihood -121.5890 Hannan-Quinn criter. 9.183287 F-statistic 3290.249 Durbin-Watson stat 0.528075 Prob(F-statistic) 0.000000由以上结果得到以下方程:^Y t=45.4022545+0.718526X t（6.1）（10.30225）（0.012526）t = (4.407025) (57.36069)R2=0.992459--R2=0.992157 F=3290.249 DW=0.528075该回归方程可决系数较高，回归系数均显著。

第六章自相关性6.1 自相关性：6.1.1. 非自相关假定由第2章知回归模型的假定条件之一是，Cov(u i, u j) = E(u i u j) = 0, (i, j∈T, i≠j), (6.1)即误差项u t的取值在时间上是相互无关的。

称误差项u t非自相关。

如果Cov (u i,u j ) ≠ 0, (i≠j)则称误差项u t存在自相关。

自相关又称序列相关。

原指一随机变量在时间上与其滞后项之间的相关。

这里主要是指回归模型中随机误差项u t与其滞后项的相关关系。

自相关也是相关关系的一种。

6.1.2．一阶自相关自相关按形式可分为两类。

(1)一阶自回归形式当误差项u t只与其滞后一期值有关时，即u t = f (u t - 1) + v t称u t具有一阶自回归形式。

(2) 高阶自回归形式当误差项u t的本期值不仅与其前一期值有关，而且与其前若干期的值都有关系时，即u t = f (u t– 1, u t– 2 , …u t– p ) + v t则称u t具有P阶自回归形式。

通常假定误差项的自相关是线性的。

因计量经济模型中自相关的最常见形式是一阶自回归形式，所以下面重点讨论误差项的线性一阶自回归形式，即u t = α1 u t -1 + v t(6.2)其中α1是自回归系数，v t 是随机误差项。

v t 满足通常假设E(v t) = 0, t = 1, 2 …,T,Var(v t) = σv2, t = 1, 2 …,T,Cov(v i , v j ) = 0, i ≠ j , i , j = 1, 2 …, T , Cov(u t -1, v t ) = 0, t = 1, 2 …, T ,依据普通最小二乘法公式，模型（6.2）中 α1 的估计公式是，1ˆa= ∑∑=-=-Tt t Tt t t u u u 22121(1ˆβ=∑---2)())((x x x x y y t t t ) (6.3)其中T 是样本容量。