高二讲义4月26日

波的多解1.波的周期性⑴波的空间周期性：波的图象上的任意质点，和与它相距波长整数倍(nλ)的多个质点的振动情况是完全相同的；⑵波的时间周期性：波的图象上的任意质点，在t时刻的振动情况与在t+nT时刻的振动图象完全相同，因此，机械波的波形总是重复出现的，这就是机械波的时间周期性。

2.波的多解问题在求解机械波类问题时，由于波传播的周期性和方向性，常常会出现多解，须对问题的隐含条件和波动的实际情况进行透彻分析。

⑴介质中质点的振动方向未定：质点振动方向与波的传播方向相联系，若某一质点振动方向未确定，则波的传播方向有两种，形成多解；⑵介质中两质点的距离与波长关系未定：在波的传播方向上，如果两个质点间的距离与波长的倍数关系不确定，即距离未知或波长未知，则易造成波的多解。

例题1图12.3-2中的实线是一列正弦波在某一时刻的波形曲线。

经0.5 s后，其波形如图中虚线所示。

设该波的周期T大于0.5 s。

（1）如果波是向左传播的，波的速度是多大？波的周期是多大？（2）如果波是向右传播的，波的速度是多大？波的周期是多大？例题2如图所示，一列简谐横波沿轴负方向传播，实线为时的波形图，虚线为时的波形图。

已知该简谐波的周期大于，关于该简谐波，下列说法错误的是（）A. 波长为B. 波速为C. 频率为D. 时，处的质点处于波谷E. 时，处的质点处于波峰例题3一列简谐波在时刻的波形如图所示，此时刻介质质点的运动方向向上，经过时间后的波形如图中虚线所示，若振源周期为，则（）A. 一定为B. 可能为C. 一定为D. 可能为例题4、两列波在某时刻的波形如图所示，经过时间(为波的周期)，两波仍出现如图波形，则两波的波速之比不可能是（）A. 2:1B. 3:1C. 1:1D. 4:3例题5如图，一列简谐横波沿一直线向左传播，当直线上某质点向上运动到达最大位移时，点右方相距的点刚好向下运动到最大位移处，则这列波的波长可能是（）A. B. C. D.。

中学生26个不良行为讲义1.不注重仪容仪表。

有的同学留长发(男生)、染发、烫发、留怪发型奇装异服，戴饰品饰物，化妆(浓)等，与中学生身份极不相符，这也是我们校规校纪所严厉禁止的，中学生还是大学生，还没有参加社会工作社会动，更不是社会闲杂人员，所以，同们要自尊自重，注重仪容仪表，否则你就会受到校规处分，或者，你有可被社会不良分子盯上，从而拉上你上违法犯罪的道路。

2.违规带手机。

几乎全国所有的中学都禁止学生带手机，我们学校也是三五申明确禁止同学们带手机，但极少同学总是置校规校纪于不顾，或心存侥幸，违规带手机，有的同学利用手机络社会闲杂人员，吃喝玩乐、打架斗殴，有的同学利用手机上网，聊天传播不良信息、下载不健康视频，有的学上课时间接听手机，影响课堂秩人有的同学午晚休时间接听电话，影响他人休息，可以说，同学们带手机有百害而无一利，如果家中有急事，家长会亲自来校或给班主任打电话，如果同学有急事，可借用任何一个老师的手机，所以同学们何苦顶风而上，冒被学校查处，回家反省的风险。

3.乱起哄。

乱起哄是非常不文明、不道德和非常危险的不良行为，有的同学在课堂、考场、餐厅、宿舍等人员聚集场所乱起哄，有的同学见到男女生一起说话乱起哄，有的同学见到其他同学发生争执乱起哄，有的同学见到其他同学出丑乱起哄，有的同学见到老师查处违纪学生就乱起哄等，乱起哄，一方面体现个人的素质修养，另一方面极易引发严重事件，如打架斗殴等，这样的例子很多，本来两个同学因小事发生口角，争执几句就没事了，但由于个别同学的乱起哄，致使矛盾升级，引发打架，至打群架等事件。

两个发生口角的同学本不想事态扩大，但此时已无法控制局势，罪魁祸首就在于乱起哄的同学望同学们高度重视，引以为戒。

4.拉帮结伙。

这是极易引发打架斗殴，甚而引发违法犯罪的不良行为，有些同学因臭味相投，拉帮拉伙，有些同学因同学关系拉帮结伙，有些同学因老乡、亲戚关系拉帮结伙，有些同学因寻求保护拉帮拉伙，有些同学因有“同是涯沦落人”的不当同感而拉帮结伙，也有的同学被迫而临时加入团伙等等，同学们讲究团体协作，共同学习，相互帮助，共同进步，这是正当的，也是大力提倡的，但是，与上面所说的拉帮结伙在本质上是不一样的，团伙内部互相激励，互相影响，胆大妄为，不计后果，什么样的坏事也敢做。

中州派紫微斗数讲义王亭之编著一、序论紫微斗数是由北宋年代开始发展的一门术数，它的前身是十八飞星。

刺激起这门术数兴起的背景，是由于当时“五星”与“子平”的竞胜。

原来我国古代推断禄命之术，最成功的是“五星”。

它根据人的出生年、月、日、时，先排成干支八字，然后由八字根据公式计算，水、火、木、金、土五星，及太阴、太阳的行度，分布于十二宫位，总称之为“七政”。

此外，另据公式布置二十八宿，及紫气，月孛，罗睺，计都等“四余”的宫度，并由此推算人的禄命。

这种算命术，因此也就称为“七政四余”。

但由于古代天文学的计算公式不精密，时间一久，即变成错宫失度，因此后来虽然有“琴堂派”兴起，另行里定“量天尺”，以及创立星嚁会合的新推断法，但依然无济于事，结果仍让“子平家“取得优势。

“子平”可以说是截取“五星”推命术的上半截而发展出来的术数。

一般相信，它兴创于唐代。

它的推算方法是仍然根据人的生年、月、日、时起干支八字，称为“四柱”，然后根据八字的阴阳五行，生剋制化，刑冲破害，三合六合，业辰诸煞等等来推算禄命，再不理会“七政四余”在十二宫的分布了。

“子平”之学，由宋代起，经历代文人学士的发展，至今已获得很大的成就，尤其是明代传为刘伯温所注的“滴天髓”，更将这门算命术发展成为哲理，清代陈素蓭相国启后承先，撰成“命理约言”，由是确立了所谓“书房派”的地位，与“江湖派”分成子平学的两大壁垒。

其实“江湖派”也不是没有优点，他们比“书房派”多实际经验，因此理论虽然有所不如，却依然能够推断准确。

一些历代相传的口诀，如“日坐比肩逢比劫，必然三度作新郎”，“癸水生人用戊官，少年定嫁白头夫”等，的确有一定的准确性。

这些口诀，不少即由实际经验积累总结而成。

所以“书房派”虽有文人学士宣扬，而“江湖派”却依然可以屹立不倒。

这等于科学的发展。

理论日日翻新，但实验却依然是理论的基础。

Xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx始构思，是针对“五星”宫度不准的缺点，选择北极星作为主星，以此计算坐标。

益智学校高二春季班讲义第二讲高考复习策略(2) 首次提出要重视对考生科学素养的考查新课程教学理念已渗透到教学和高考中新课程教学目标：知识和技能；过程和方法态度、情感和价值观四省市新课程高考：1.保持全国高考要求一致和稳定2.增加摸块选作题，提供选择性3.强调了过程和方法，注重探究和评价经过8年的理科综合考试实践，考试模式已经较为成熟，积累了丰富的命题经验，可以相信今后处于相对稳定状态，但随课改进行，依然会稳中有变。

二、复习建议1．合理制定教学目标重视基础、理顺思路2.处理好新题型与传统题型的关系* 重视传统题型对基本能力的培养* 注意新题型对观察问题、发现问题和解决问题的能力的培养3.处理好主干知识与非主干知识的关系(1) 通过典型例题，加深对主干、核心规律的理解领悟复习不是简单重复，把知识结构化、系统化的目的是抓住核心，居高临下，融会贯通。

站在力和运动关系高度理解力、理解各种运动形式：(98)如图所示，在x轴上方有垂直于xy平面向里的匀强磁场，磁感应强度为B；在x轴下方有沿y轴负方向的匀强电场，场强为E.一质量为m，电量为-q的粒子从坐标原点O沿着x轴正方向射出，射出之后，第三次到达x轴时，它与原点O的距离为L. 求此粒子射出时的速度v0和运动的总路程s (重力不计).(06理2) 25．（16分）如图所示，在x<0与x>0的区域中，存在磁感应强度大小分别为B1与B2的匀强磁场，磁场方向均垂直于纸面向里，且B1>B2。

一个带负电荷的粒子从坐标原点O以速度v沿x轴负方向射出，要使该粒子经过一段时间后又经过O点，B1与B2的比值应满足什么条件？(04理Ⅲ) 24．(18分) 如图所示，在y>0的空间中存在匀强电场，场强沿y轴负方向；在y<0的空间中，存在匀强磁场，磁场方向垂直xy平面(纸面)向外。

一电量为q、质量为m的带正电的运动粒子，经过y轴上x=h处的点P1时速率为v0，方向沿x轴正方向；然后，经过x 轴上x =2h 处的P 2点进入磁场，并经过轴上y =-2h 处的P 3点。

第一章地球的运动第二节地球运动的地理意义（第2课时）课程标准课标解读结合实例，说明地球运动的地理意义。

1.结合实例分析，理解昼夜长短变化的规律。

2．通过观察总结，掌握正午太阳高度的变化规律。

3．结合材料，分析四季更替的原因及五带的划分。

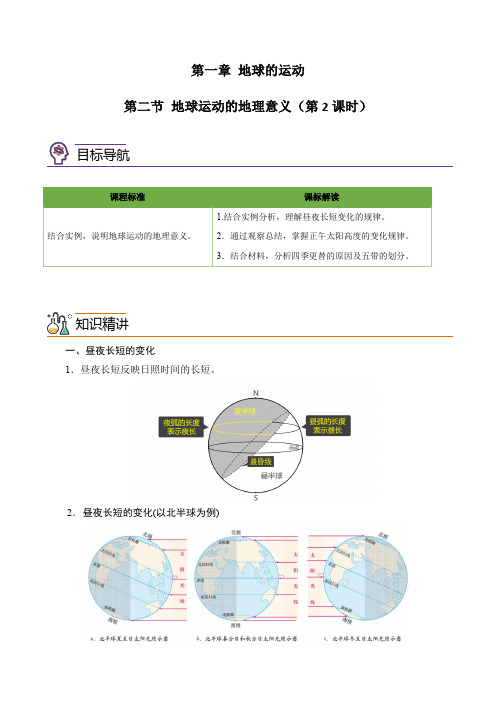
一、昼夜长短的变化1．昼夜长短反映日照时间的长短。

2．昼夜长短的变化(以北半球为例)目标导航知识精讲时间昼夜长短分布规律特殊现象夏半年昼长夜短纬度越高，昼越长，夜越短，至北极四周为极昼夏至日太阳直射北回归线，北半球昼最长、夜最短，北极圈及其以北地区皆为极昼冬半年昼短夜长纬度越高，昼越短，夜越长，至北极四周有极夜现象冬至日太阳直射南回归线，北半球昼最短、夜最长，北极圈及其以北地区出现极夜现象春秋分日昼夜等长均为12时【微点拨】(1)太阳直射某地，该地不一定昼最长、夜最短，北半球各地夏至日这一天昼最长，南半球各地冬至日这一天昼最长。

(2)太阳直射点的纬度越高，地球上各地昼夜相差越大，出现极昼、极夜的范围越大。

(3)同一纬线上各地同一天的昼夜长短相等(日出、日落地方时也相同)；同一纬线的昼夜长短在一年中有两个日期相同(除二至日)，且这两个日期近似关于二至日对称。

【知识拓展】昼夜长短变化的规律：(1)对称规律：同一纬线上各地昼夜长短相同(同线等长)；南北半球同纬度昼夜长短相反。

二分日前后时间相同的两日期，昼夜长短相反。

二至日前后时间相同的两日期，昼夜长短相同。

(2)递增规律：大阳直射点所在半球昼长夜短，且纬度越高，昼越长；另一半球相反。

(3)变幅规律：赤道处全年昼夜平分；纬度越高，昼夜长短的变化幅度越大。

(4)极昼、极夜规律：极昼(极夜)的起始纬度＝90°－太阳直射点的纬度。

纬度越高，极昼(极夜)出现的天数越多。

【即学即练1】2020年2月底，我国黄河站空间物理观测台（11°56＇E，78°55＇N）迎来了当年极夜之后的首次日出。

据此完成下面小题。

高二数学人教B版选修4-5讲义案【第一章：1.5.3反证法和放缩法】[读教材·填要点]1．反证法首先假设要证明的命题是不正确的，然后利用公理，已有的定义、定理，命题的条件逐步分析，得到和命题的条件(或已证明过的定理，或明显成立的事实)矛盾的结论，以此说明假设的结论不成立，从而原来结论是正确的，这种方法称为反证法．2．放缩法在证明不等式时，有时需要将所需证明的不等式的值适当放大(或缩小)使它由繁化简，达到证明目的，这种方法称为放缩法．[小问题·大思维]1．用反证法证明不等式应注意哪些问题？提示：用反证法证明不等式要把握三点：(1)必须先否定结论，对于结论的反面出现的多种可能要逐一论证，缺少任何一种可能，证明都是不完全的．(2)反证法必须从否定结论进行推理，且必须根据这一条件进行论证；否则，仅否定结论，不从结论的反面出发进行论证，就不是反证法．(3)推导出来的矛盾可以是多种多样的，有的与已知条件相矛盾，有的与假设相矛盾，有的与定理、公理相违背，有的与已知的事实相矛盾等，但推导出的矛盾必须是明显的．2．运用放缩法证明不等式的关键是什么？提示：运用放缩法证明不等式的关键是放大(或缩小)要适当．如果所要证明的不等式中含有分式，那么我们把分母放大时相应分式的值就会缩小；反之，如果把分母缩小，则相应分式的值就会放大．有时也会把分子、分母同时放大，这时应该注意不等式的变化情况，可以与相应的函数相联系，以达到判断大小的目的，这些都是我们在证明中的常用方法与技巧，也是放缩法中的主要形式．[对应学生用书P21][例1] 设a ，b ，c ，d 都是小于1的正数，求证：4a (1－b )，4b (1－c )，4c (1－d )，4d (1－a )这四个数不可能都大于1.[思路点拨] 本题考查反证法的应用．解答本题若采用直接法证明将非常困难，因此可考虑采用反证法从反面入手解决．[精解详析] 假设4a (1－b )＞1,4b (1－c )＞1,4c (1－d )＞1，4d (1－a )＞1，则有a (1－b )＞14，b (1－c )＞14， c (1－d )＞14，d (1－a )＞14.∴a (1－b )＞12，b (1－c )＞12，c (1－d )＞12，d (1－a )＞12. 又∵a (1－b )≤a ＋(1－b )2，b (1－c )≤b ＋(1－c )2， c (1－d )≤c ＋(1－d )2，d (1－a )≤d ＋(1－a )2， ∴a ＋1－b 2＞12，b ＋1－c 2＞12， c ＋1－d 2＞12，d ＋1－a 2＞12. 将上面各式相加得2＞2，矛盾．∴4a (1－b )，4b (1－c )，4c (1－d )，4d (1－a )这四个数不可能都大于1.(1)当证明的结论中含有“不是”，“不都”，“不存在”等词语时，适于应用反证法，因为此类问题的反面比较具体．(2)用反证法证明不等式时，推出的矛盾有三种表现形式①与已知相矛盾，②与假设矛盾，③与显然成立的事实相矛盾．1．已知数列{a n}的前n项和为S n，且满足a n＋S n＝2.(1)求数列{a n}的通项公式；(2)求证数列{a n}中不存在三项按原来顺序成等差数列．解：(1)当n＝1时，a1＋S1＝2a1＝2，则a1＝1.又a n＋S n＝2，所以a n＋1＋S n＋1＝2，两式相减得a n＋1＝12a n，所以{a n }是首项为1，公比为12的等比数列， 所以a n ＝12n －1. (2)反证法：假设存在三项按原来顺序成等差数列，记为a p ＋1，a q ＋1，a r ＋1(p <q <r ，且p ，q ，r ∈N ＋)，则2·12q ＝12p ＋12r ，所以2·2r －q ＝2r －p ＋1.①又因为p <q <r ，所以r －q ，r －p ∈N ＋.所以①式左边是偶数，右边是奇数，等式不成立，所以假设不成立，原命题得证.[例2] 若a ，b ，c 均为实数，且a ＝x 2－2y ＋π2，b ＝y 2－2z ＋π3，c ＝z 2－2x ＋π6，求证：a ，b ，c中至少有一个大于0.[思路点拨] 由于问题是“至少型”命题，故可用反证法证明．[精解详析] 假设a ，b ，c 都不大于0，即a ≤0，b ≤0，c ≤0，则a ＋b ＋c ≤0，而a ＋b ＋c ＝x 2－2y ＋π2＋y 2－2z ＋π3＋z 2－2x ＋π6＝(x －1)2＋(y －1)2＋(z －1)2＋π－3∴π－3>0，且(x －1)2＋(y －1)2＋(z －1)≥0∴a ＋b ＋c >0这与a ＋b ＋c ≤0矛盾．因此，a ，b ，c 中至少有一个大于0.(1)在证明中含有“至少”、“至多”、“最多”等字眼时，或证明否定性命题、惟一性命题时，可使用反证法证明．在证明中常见的矛盾可以与题设矛盾，也可以与已知矛盾，与显然的事实矛盾，也可以自相矛盾．(2)在用反证法证明的过程中，由于作出了与结论相反的假设，相当于增加了题设条件，因此在证明过程中必须使用这个增加的条件，否则将无法推出矛盾．2．实数a，b，c，d满足a＋b＝c＋d＝1，ac＋bd>1.求证：a，b，c，d中至少有一个是负数．证明：假设a，b，c，d都是非负数，即a≥0，b≥0，c≥0，d≥0，则1＝(a＋b)(c＋d)＝(ac＋bd)＋(ad＋bc)≥ac＋bd.这与已知中ac＋bd>1矛盾，∴原假设错误，故a ，b ，c ，d 中至少有一个是负数.[例3] 求证：32－1n ＋1＜1＋122＋…＋1n 2＜2－1n (n ∈N *且n ≥2)． [思路点拨] 本题考查放缩法在证明不等式中的应用，解答本题要注意欲证的式子中间是一个和的形式，但我们不能利用求和公式或其他方法求和，因此可考虑将分母适当放大或缩小成可以求和的形式，进而求和，并证明该不等式．[精解详析] ∵k (k ＋1)＞k 2＞k (k －1)，∴1k (k ＋1)＜1k 2＜1k (k －1). 即1k －1k ＋1＜1k 2＜1k －1－1k(k ∈N ＋且k ≥2)． 分别令k ＝2,3，…，n 得12－13＜122＜1－12，13－14＜132＜12－13， … 1n －1n ＋1＜1n 2＜1n －1－1n ，将这些不等式相加得12－13＋13－14＋…＋1n －1n ＋1＜122＋132＋…＋1n 2＜1－12＋12－13＋…＋1n －1－1n， 即12－1n ＋1＜122＋132＋…＋1n 2＜1－1n . ∴1＋12－1n ＋1＜1＋122＋132＋…＋1n 2＜1＋1－1n. 即32－1n ＋1＜1＋122＋132＋…＋1n 2＜2－1n (n ∈N ＋且n ≥2)成立．(1)放缩法证不等式主要是根据不等式的传递性进行变换，即欲证a >b ，可换成证a >c 且c >b ，欲证a <b ，可换成证a <c 且c <b .(2)放缩法是不等式证明中最重要的变形方法之一，放缩必须有目标．而且要恰到好处，目标往往要从证明的结论考察．常用的放缩方法有增项、减项、利用分式的性质、利用不等式的性质、利用已知不等式、利用函数的性质进行放缩等．比如：舍去或加上一些项：⎝⎛⎭⎫a ＋122＋34＞⎝⎛⎭⎫a ＋122； 将分子或分母放大(缩小)：1k 2＜1k (k －1)，1k 2＞ 1k (k ＋1)，1k ＜2k ＋k －1，1k ＞2k ＋k ＋1(k ∈R ，k ＞1)等．3．设n 是正整数，求证：12≤1n ＋1＋1n ＋2＋…＋12n <1.证明：由2n ≥n ＋k ≥n (k ＝1,2…，n )，得12n ≤1n ＋k <1n. 当k ＝1时，12n ≤1n ＋1<1n； 当k ＝2时，12n ≤1n ＋2<1n ； …当k ＝n 时，12n ≤1n ＋n <1n， ∴12＝n 2n ≤1n ＋1＋1n ＋2＋…＋12n <n n＝1.[对应学生用书P23]一、选择题1．否定“自然数a 、b 、c 中恰有一个为偶数”时正确的反设为( )A ．a 、b 、c 都是奇数B ．a 、b 、c 都是偶数C ．a 、b 、c 中至少有两个偶数D ．a 、b 、c 中至少有两个偶数或都是奇数解析：三个自然数的奇偶情况有“三偶、三奇、二偶一奇、二奇一偶”4种，而自然数a 、b 、c 中恰有一个为偶数包含“二奇一偶”的情况，故反面的情况有3种，只有D 项符合．答案：D2．设M ＝1210＋1210＋1＋1210＋2＋…＋1211－1，则( ) A ．M ＝1B ．M <1C ．M >1D ．M 与1大小关系不定解析：∵210＋1>210,210＋2>210，…，211－1>210，∴M ＝1210＋1210＋1＋1210＋2＋…＋1211－1 <101010102111···222+++144424443个＝1.答案：B3．设a ，b ，c ∈(－∞，0)，则三数a ＋1b ，b ＋1c ，c ＋1a 的值( )A ．都不大于－2B ．都不小于－2C ．至少有一个不大于－2D ．至少有一个不小于－2解析：假设都大于－2，则a ＋1b ＋b ＋1c ＋c ＋1a ＞－6，∵a ，b ，c ＜0，∴a ＋1a ≤－2，b ＋1b ≤－2，c ＋1c ≤－2，∴a ＋1a ＋b ＋1b ＋c ＋1c ≤－6，这与假设矛盾，则选C.答案：C4．已知p ＝a ＋1a －2，q ＝－a 2＋4a (a >2)，则( ) A ．p >qB ．p <qC ．p ≥qD ．p ≤q 解析：∵p ＝(a －2)＋1a －2＋2，又a －2>0， ∴p ≥2＋2＝4，而q ＝－(a －2)2＋4，由a >2，可得q <4，∴p >q .答案：A二、填空题5．给出下列两种说法：①已知p 3＋q 3＝2，求证p ＋q ≤2，用反证法证明时，可假设p ＋q ≥2；②已知a ，b ∈R ，|a |＋|b |<1，求证方程x 2＋ax ＋b ＝0的两根的绝对值都小于1，用反证法证明时，可假设方程有一根x 1的绝对值大于或等于1，即假设|x 1|≥1.以上两种说法正确的是________．解析：反证法的实质是否定结论，对于①，其结论的反面是p ＋q >2，所以①错误；对于②，其假设正确．答案：②6．用反证法证明“已知平面上有n (n ≥3)个点，其中任意两点的距离最大为d ，距离为d 的两点间的线段称为这组点的直径，求证直径的数目最多为n 条”时，假设的内容为________．解析：对“至多”的否定应当是“至少”，二者之间应该是完全对应的，所以本题中的假设应为“直径的数目至少为n ＋1条”．答案：直径的数目至少为n ＋1条7．A ＝1＋12＋13＋…＋1n 与n (n ∈N ＋)的大小关系是________．解析：A ＝11＋12＋13＋ (1)≥＝nn＝n.答案：A ≥n8．设a >0，b >0，M ＝a ＋ba ＋b ＋2，N ＝aa ＋2＋bb ＋2，则M 与N 的大小关系是________．解析：∵a >0，b >0，∴N ＝a a ＋2＋bb ＋2>aa ＋b ＋2＋ba ＋b ＋2＝a ＋ba ＋b ＋2＝M .∴M <N .答案：M <N三、解答题9．已知0<x <2,0<y <2,0<z <2，求证：x (2－y )，y (2－z )，z (2－x )不都大于1. 证明：法一：假设x (2－y )>1且y (2－z )>1且z (2－x )>1均成立，则三式相乘有：xyz (2－x )(2－y )(2－z )>1. ① 由于0<x <2，∴0＜x (2－x )＝－x 2＋2x ＝－(x －1)2＋1≤1.同理：0＜y (2－y )≤1，且0＜z (2－z )≤1，∴三式相乘得：0<xyz (2－x )(2－y )(2－z )≤1 ② ②与①矛盾，故假设不成立．∴x (2－y )，y (2－z )，z (2－x )不都大于1.法二：假设x (2－y )＞1且y (2－z )＞1且z (2－x )＞1.∴x (2－y )＋y (2－z )＋z (2－x )＞3. ③ 又x (2－y )＋y (2－z )＋z (2－x )+?··+n 44项≤x ＋(2－y )2＋y ＋(2－z )2＋z ＋(2－x )2＝3 ④ ④与③矛盾，故假设不成立，∴原题设结论成立．10．已知实数x 、y 、z 不全为零，求证： x 2＋xy ＋y 2＋ y 2＋yz ＋z 2＋ z 2＋zx ＋x 2>32(x ＋y ＋z )． 证明：x 2＋xy ＋y 2＝ ⎝⎛⎭⎫x ＋y22＋34y 2≥ ⎝⎛⎭⎫x ＋y22 ＝|x ＋y 2|≥x ＋y2. 同理可得：y 2＋yz ＋z 2≥y ＋z2，z 2＋zx ＋x 2≥z ＋x 2.由于x 、y 、z 不全为零，故上述三式中至少有一式取不到等号，所以三式累加得： x 2＋xy ＋y 2＋y 2＋yz ＋z 2＋z 2＋zx ＋x 2>⎝⎛⎭⎫x ＋y 2＋⎝⎛⎭⎫y ＋z 2＋⎝⎛⎭⎫z ＋x 2＝32(x ＋y ＋z )．11．设数列{a n }的前n 项和为S n ，a 1＝1，S n ＝na n －2n (n －1)．(1)求数列{a n }的通项公式a n ；(2)设数列⎩⎨⎧⎭⎬⎫1a n a n ＋1的前n 项和为T n ，求证：15≤T n <14.解：(1)由S n ＝na n －2n (n －1)得a n ＋1＝S n ＋1－S n ＝(n ＋1)a n ＋1－na n －4n ，即a n ＋1－a n ＝4.∴数列{a n }是以1为首项，4为公差的等差数列，∴a n ＝4n －3.(2)证明：T n ＝1a 1a 2＋1a 2a 3＋…＋1a n a n ＋1＝11×5＋15×9＋19×13＋…＋1(4n －3)×(4n ＋1)＝14⎝ ⎛⎭⎪⎫1－15＋15－19＋19－113＋…＋14n －3－14n ＋1 ＝14⎝ ⎛⎭⎪⎫1－14n ＋1<14. 又易知T n 单调递增，故T n ≥T 1＝15，得15≤T n <14.。

唯物辩证法的联系观一、联系的普遍性原理1、〖原理内容〗：唯物辩证法认为，所谓联系，就是事物之间以及事物内部诸要素之间的相互影响、相互制约和相互作用。

联系是普遍的。

世界上一切事物都与周围其他事物有着这样或那样的联系。

每一个事物内部的各个部分、要素之间是相互联系的。

世界是一个普遍联系的有机整体，是一幅由种种联系交织起来的丰富多彩的画面，其中没有一个事物是孤立存在的。

2、〖方法论〗：要用联系的观点看问题，反对用孤立的观点看问题。

既要看到事物之间的联系，又要看到事物内部诸要素之间的联系。

3、〖反对〗：反对切忌割裂事物之间的联系，用形而上学孤立的的观点来认识和处理问题。

二、联系的客观性原理1、〖原理内容〗：唯物辩证法认为，联系是客观的。

联系是事物本身所固有的，不以人的意志为转移。

（自在事物和人为事物的联系都是客观的）2、〖方法论〗：①要从事物固有的联系中把握事物，切忌主观随意性。

②联系是客观的，并不意味着人对事物的联系无能为力，人们可以根据事物固有的联系，改变事物的状态，调整原有的联系，建立新的联系。

3、〖反对〗：反对否定事物的联系，或主观臆造联系，把本来不存在的联系强加给事物。

三、联系的多样性原理1、〖原理内容〗：唯物辩证法认为，世界上的事物千差万别，事物的联系也是多种多样的。

2、〖方法论〗：要求我们注意分析和把握事物存在和发展的各种条件。

我们在认识世界和改造世界的过程中，既要注重客观条件，又要恰当运用自身的主观条件；既要把握事物的内部条件，又要关注事物的外部条件；既要认识事物的有利条件，又要重视事物的不利条件。

总之。

要一切以时间、地点、条件为转移。

3、〖反对〗：反对以一种联系概括事物之间多种多样的不同联系，否认联系的多样性。

四、联系的条件性原理1、〖原理内容〗：事物之间都是有条件地联系着的，无条件的联系是不存在的。

任何具体的联系都依赖于一定条件，随着条件的改变，事物之间及事物内部因素之间的联系的性质、方式也要发生变化。