整式的乘除与因式分解知识结构图
- 格式:doc
- 大小:179.39 KB
- 文档页数:1


新课标人教版初中数学八年级上册第十五章《整式的乘除与因式分解》简介人教版《义务教育课程标准实验教科书?数学》第十五章是“整式的乘除与因式分解”。
本章的主要内容是整式的乘除运算、乘法公式以及因式分解。
本章内容建立在已经学习了的有理数运算、列简单的代数式、一次方程及不等式、整式的加减运算等知识的基础上。
整式的乘除运算和因式分解是基本而重要的代数初步知识,这些知识是以后学习分式和根式运算、函数等知识的基础,在后续的数学学习中具有重要意义,同时,这些知识也是学习物理、化学等学科及其他科学技术不可缺少的数学基础知识.本章共安排了4个小节,教学时间约需13课时(供参考):15.1 整式的乘法4课时15.2 乘法公式2课时15.3 整式的除法2课时15.4 因式分解3课时数学活动小结2课时一、教科书内容和课程学习目标(一)本章知识结构框图(二)教科书内容本章共包括4节15.1 整式的乘法整式的乘法是整式四则运算的重要组成部分。
本节分为四个小节,主要内容是整式的乘法,这些内容是在学生掌握了有理数运算、整式加减运算等知识的基础上学习的。
其中,幂的运算性质,即同底数幂的乘法、幂的乘方和积的乘方是整式乘法的基础,教科书把它们依次安排在前三个小节中,教学中应适当复习幂、指数、底数等概念,特别要弄清正整数指数幂的意义。
在学生掌握了幂的运算性质后,作为它们的一个直接应用,教科书在第四小节安排一般整式乘法的教学内容。
首先是单项式与单项式相乘,由于进行单项式与多项式、多项式与多项式相乘的前提是熟练地进行单项式与单项式相乘,因此,对于单项式与单项式相乘的教学应该予以充分重视。
在学生掌握了单项式与单项式相乘的基础上,教科书利用分配律等进一步引入单项式与多项式相乘、多项式与多项式相乘,这样使整式乘法运算的教学从简到繁,由易到难,层层递进。
15.2乘法公式本节分为两个小节,分别介绍平方差公式与完全平方公式。
乘法公式是整式乘法的特殊情形,是在学习了一般的整式乘法知识的基础上学习的,运用乘法公式能简化一些特定类型的整式相乘的运算问题,教科书在本节开始首先指出了这一点。



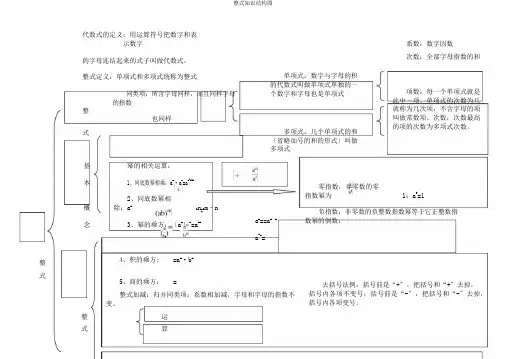
代数式的定义:用运算符号把数字和表示数字整的字母连结起来的式子叫做代数式。
式整式定义:单项式和多项式统称为整式整同类项:所含字母同样,而且同样字母的指数也同样式单项式:数字与字母的积的代数式叫做单项式单独的一个数字和字母也是单项式多项式:几个单项式的和〔省略加号的和的形式〕叫做多项式系数:数字因数次数:全部字母指数的和项数:每一个单项式就是此中一项。
单项式的次数为几就称为几次项,不含字母的项叫做常数项。
次数:次数最高的项的次数为多项式次数。
基幂的相关运算:本1、同底数幂相乘:a m·a n=a m+nam概2、同底数幂相除:a m a n=a m–n念3、幂的乘方:〔a m〕n=a mn零指数:非零数的零指数幂为1:a0=1a n==a m–n负指数:非零数的负整数指数幂等于它正整数指数幂的倒数:a-p=整式4、积的乘方: =a m·b m5、商的乘方:=整式加减:归并同类项:系数相加减,字母和字母的指数不变。
去括号法例:括号前是“+〞,把括号和“+〞去掉,括号内各项不变号;括号前是“-〞,把括号和“-〞去掉,括号内各项变号。
整式运算整式乘法:1、单项式相乘:单项式与单项式相乘,把他们的系数,同样字母分别相乘,关于只在一个单项式里含有的字母,那么连同它的指数作为积的一个因式。
2、单项式乘以多项式,就是用单项式去乘多项式的每一项,再把所得的积相加。
m(a b c) ma mb mc3、多项式与多项式相乘,先用多项式的每一项乘以另一个多项式的每一项,再把所的的积相加。
m+n〕(a+b+c)=ma+mb+mc+na+nb+nc乘法公式:平方差公式:(ab)(ab)a2b2完整平方公式:(ab)2a22ab2整式除法:同分式运算整式乘方:幂的相关运算。

同底数幂的乘法:m n a a •= 同底数幂相乘,底数不变,指数相加 幂的乘方:()n m a = 幂的乘方,底数不变,指数相乘 积的乘方:a n n
b = 积的每一个因式分别乘方,再把所得的幂相
乘
同底数幂的除法:
a m n a ÷= (a 0≠,m,n 都是
正整数,并且m>n )
同底数幂相除,底数不变,指数相减
0a = a 0≠()
任何不等于0的数的0次幂都等于
整式的乘法
单项式与单项式相乘,把它们的系数、字母 ,对于只在一个单项式里含有的字母,则连同它的指数作为积
的 。
如:52
ac bc =g
单项式与多项式相乘,就是用单项式去乘
多项式的 ,再把所的积
如:22132(2)ab ab ab -=g
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的 ,再把所得的积相加
如:(8)()x y x y --= 乘法 公式
平方差公式:
(a+b)(a-b)=
两个数的 与这两个数的 的积,等于这两个数的
完全平方公式:
2
a+b =() 2a b -=()
添括号的法则:
添括号时,如果括号前面是正号,括到括号里的各项都 ;如果括号前面是负号,括到括号里的各项都 。
如:a b c ++=
a b c --=
单项式相除,把系数与同底数幂 作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的 。
如:42328x y 7x y ÷=
整式 的除法
多项式除以单项式,先把这个多项式的 除以这个单项式,再把所得的 如:3212a 63)3a a a -+÷=(
把一个多项式化成几个整式的 ,这样的式子的变形叫做把这个多项式 。
也叫做把这个多项式 。
因式分 解
整式乘除
与 因式分解
提公因式法:
2a()3()b c b c +-+=
公式法:
22a b -=
22
a +2ab+
b = 22a -2ab+b =
22()()x p x q +-+=。