5坐标系中的位似变换(2016年)

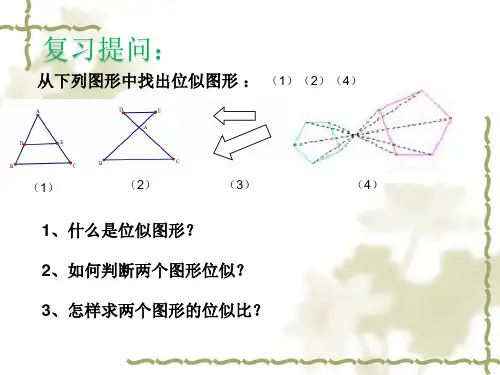
北师大版数学九年级上册《平面直角坐标系中的位似》说课稿1一. 教材分析《平面直角坐标系中的位似》是北师大版数学九年级上册第五章《几何变换》中的一个知识点。

本节课主要让学生了解位似的概念，掌握位似变换的性质及位似变换在实际问题中的应用。

教材通过生活中的实例引入位似的概念，让学生在具体的情境中感受数学与生活的紧密联系。

二. 学情分析九年级的学生已经学习了平面直角坐标系、函数等基础知识，对图形的变换有一定的了解。

但在实际应用中，学生可能对位似变换的理解和运用还存在一定的困难。

因此，在教学过程中，要注重引导学生从实际问题中抽象出位似变换的概念，培养学生运用数学知识解决实际问题的能力。

三. 说教学目标1.知识与技能：理解位似的概念，掌握位似变换的性质，能运用位似变换解决实际问题。

2.过程与方法：通过观察、操作、思考、交流等活动，培养学生的抽象思维能力和空间想象能力。

3.情感态度与价值观：感受数学与生活的紧密联系，培养学生运用数学知识解决实际问题的意识。

四. 说教学重难点1.重点：位似的概念，位似变换的性质。

2.难点：位似变换在实际问题中的应用。

五. 说教学方法与手段1.教学方法：采用问题驱动法、案例教学法、小组合作学习法等。

2.教学手段：多媒体课件、几何画板、实物模型等。

六. 说教学过程1.导入新课：通过展示生活中的实例，引导学生关注位似现象，激发学生的学习兴趣。

2.自主学习：让学生通过阅读教材，了解位似的概念，总结位似变换的性质。

3.合作交流：学生分组讨论，分享学习心得，互相解答疑问。

4.教师讲解：针对学生讨论中的共性问题，进行讲解和解答。

5.练习巩固：让学生通过练习题，巩固所学知识。

6.拓展应用：结合实际问题，让学生运用位似变换解决问题。

7.总结反思：让学生总结本节课的学习收获，反思自己的学习过程。

七. 说板书设计板书设计要清晰、简洁、有条理，突出位似的概念和位似变换的性质。

可以采用列表、图示等方式，帮助学生理解和记忆。

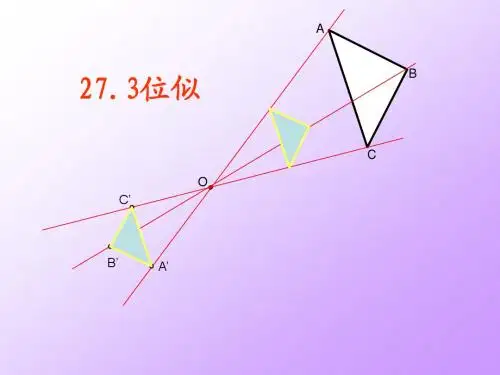
第3章图形的相似
3.6 位似
【应用举例】
例1 [教材P99例] 如图3－6－44，在平面直角坐标系中，已知平行四边形OABC的顶点坐标分别为O(0，0)，A(3，0)，B(4，2)，C(1，2)．以坐标原点O为位似中心，将OABC放大为原图形的3倍．
图3－6－44
图3－6－45
解：将平行四边形OABC的各顶点的坐标分别乘3，得O(0，0)，A′(9，0)，B′(12，6)，C′(3，6)，依次连接点O，A′，B′，C′，则四边形OA′B′C′即为所要求的图形，如图3－6－45所示．
变式一如图3－6－46，在直角坐标系中，四边形OABC 的顶点坐标分别是O(0，0)，A(3，0)，B(4，4)， C(－2，3)．画出四边形OABC以O为位似中心的位似图形，使它与四边形OABC的位似比是2∶1.
图3－6－46
变式二如图3－6－47，在平面直角坐标系中，以原点O为位似中心，用上一节课的方法画出五边形OBCDE的位似图形，使它与五边形OBCDE的位似比为1∶2.比较两个图形对应点的坐标，你能发现什么？。

初中数学例题：坐标系中的位似图形3.（2015•漳州）如图，在10×10的正方形网格中，点A，B，C，D均在格点上，以点A为位似中心画四边形AB′C′D′，使它与四边形ABCD位似，且相似比为2．（1）在图中画出四边形AB′C′D′；（2）填空：△AC′D′是三角形．【思路点拨】（1）延长AB到B′，使AB′=2AB，得到B的对应点B′，同样得到C、D的对应点C′，D′，再顺次连接即可；（2）利用勾股定理求出AC′2=42+82=80，AD′2=62+22=40，C′D′2=62+22=40，那么AD′=C′D′，AD′2+C′D′2=AC′2，即可判定△AC′D′是等腰直角三角形．【答案与解析】解：（1）如图所示：（2）∵AC′2=42+82=16+64=80，AD′2=62+22=36+4=40，C′D′2=62+22=36+4=40，∴AD′=C′D′，AD′2+C′D′2=AC′2，∴△AC′D′是等腰直角三角形．故答案为：等腰直角．【总结升华】本题考查了作图﹣位似变换．画位似图形的一般步骤为：①确定位似中心，②分别连接并延长位似中心和能代表原图的关键点；③根据相似比，确定能代表所作的位似图形的关键点；顺次连接上述各点，得到放大或缩小的图形．同时考查了勾股定理及其逆定理等知识．熟练掌握网格结构以及位似变换的定义是解题的关键．4.（2016春•威海期末）如图△ABC的顶点坐标分别为A（1，1），B（2，3），C（3，0）．（1）以点O为位似中心画△DEF，使它与△ABC位似，且相似比为2．（2）在（1）的条件下，若M（a，b）为△ABC边上的任意一点，则△DEF的边上与点M对应的点M′的坐标为．【思路点拨】（1）把点A、B、C的横、纵坐标都乘以2可得到对应点D、E、F 的坐标，再描点可得△DEF；把点A、B、C的横、纵坐标都乘以﹣2可得到对应点D′、E′、F′的坐标，然后描点可得△D′E′F′；（2）利用以原点为位似中心的位似变换的对应点的坐标特征求解．【答案与解析】解：（1）如图，△DEF和△D′E′F′为所作；（2）点M对应的点M′的坐标为（2a，2b）或（﹣2a，﹣2b）．故答案为（2a，2b）或（﹣2a，﹣2b）．【总结升华】本题考查了位似变换：如果两个图形不仅是相似图形，而且对应顶点的连线相交于一点，对应边互相平行，那么这样的两个图形叫做位似图形，这个点叫做位似中心．在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或﹣k．举一反三：【变式】如图，将△AOB中各顶点的纵坐标，横坐标分别乘-1，•得到的图形与原图形相比有什么变化？作出所得的图形，这个过程可以看作是一个什么图形变换？【答案】解：图形的形状和大小都没有变化；可以看作是△AOB绕O•点按逆时针方向旋转180°得到的.。