第八届中环杯四年级决赛

最大与最小知识要点在日常生活和工作中，经常会遇到这样一类问题：怎样安排时间最省、怎样行走路线最短、怎样管理费用最低、怎样设计面积最大、怎样合作效率最高、怎样加工利用率最大等等，它们都可以归结为在一定条件下的最大值或最小值方面的数学问题。

最大和最小都是在某一固定范围內比较的结果。

固定的范围就是一个定值，抓住这个“定值”就抓住了解题的关键。

解决极值问题的策略，常常因题而异，归纳起来主要有以下四个“突破口”：①从极端情况入手；②用枚举比较入手；③由分析推理入手；④凭构造方程入手。

最小1.（2008年4月13日第六届小学“希望杯”全国数学邀请赛五年级第2试第4题）有一排椅子有27个座位，为了使后去的人随意坐在哪个位置都有人与他相邻，则至少要先坐_______人。

2.圆桌周围恰好有12把椅子，现在已经有一些人在桌边就坐。

当再有一人入座时，就必须和已就坐的某人相邻。

问：已就坐的最少有多少人？3.阶梯教室座位有10排，每排有16个座位，当有150个人就座时，某些排坐着的人数就一样多。

我们希望人数一样的排数尽可能少，这样的排数至少有多少排？4.（2007年台湾第十一届小学数学世界邀请赛个人赛第6题）商店里销售的铅笔有两种包装，五支包装的每包售价6元，七支包装的每包售价7元。

某校至少要购买铅笔111支，请问至少要花费_______元。

5.若干名家长（爸爸或妈妈，他们都不是老师）和老师陪同一些小学生参加某次数学竞赛，已知家长和老师共有22人，家长比老师多，妈妈比爸爸多，女老师比妈妈多2人，至少有1名男老师，那么在这22人中，爸爸有多少人？6.（2007年“我爱数学夏令营”综合测试题第7题）一个小公司有5个职工，月平均工资为2700元。

已知最高工资是最低工资的2倍，那么最高月工资最少为_______元。

7.（1999年第八届日本小学数学奥林匹克大赛决赛第7题）有一批货物，它们的总重量是19500千克，不知道每一件货物的重量，但没有一件货物的重量超过350千克。

1、我们把研究路程、速度、时间以及这三者之间关系的一类问题，总称为行程问题.而行程问题的最基本关系式为：路程=速度×时间.2、两个物体以不同的点作为起点作相向运动的问题，称为相遇问题.3、相遇问题中的基本数量关系式（常考虑两个物体或人（甲、乙）的速度和）： ①相遇路程=甲走的路程+乙走的路程=甲的速度×相遇时间+乙的速度×相遇时间=（甲的速度+乙的速度）×相遇时间=速度和×相遇时间②相遇时间=相遇路程÷速度和③速度和=相遇路程÷相遇时间甲乙两车分别从相距800千米的两地同时出发相向而行，甲车每小时行52千米，乙车每小时行48千米，问（1）几小时后两车还相距200千米？（2）几小时后两车相遇？（3）几小时后两车相遇又相距200千米？分析：（1）第一次相距200千米时，说明还有200米没有行，在800千米中必须减掉200千米；（2）共同行驶800千米时两车相遇；（3）再次相距200千米时，共同行驶了1000200800＝＋（千米）解：（1）64852200800）＝＋（）（÷-（小时）（2）84852800）＝＋（÷（小时）（3）104852200800）＝＋（）＋（÷（小时）答：6小时后两车还相距200千米，8小时后两车相遇，10小时后两车还相距200千米。

甲、乙两人分别从相距300千米的A 、B 两地同时沿笔直的公路乘车相向而行，各自前往B 地、A 地。

甲每小时行32千米，乙每小时行18千米。

甲、乙各有一个对讲机，当他们之间的距离小于50千米时，两人可用对讲机联络。

问：（1）两人出发后多久才可以用对讲机联络？（2）他们用对讲机联络后，经过多长时间相遇？（3）他们可用对讲机联络多长时间？解：（1）5183250300=+÷-）（）（（小时）（2）1183250=+÷）（（小时）（3）21832250=+÷⨯）（（小时）A 、B 两地相距520千米，甲车从A 地开出2小时后，乙车从B 地相向开出，乙车开出后5小时与甲车相遇，已知甲车比乙车每小时少行8千米。

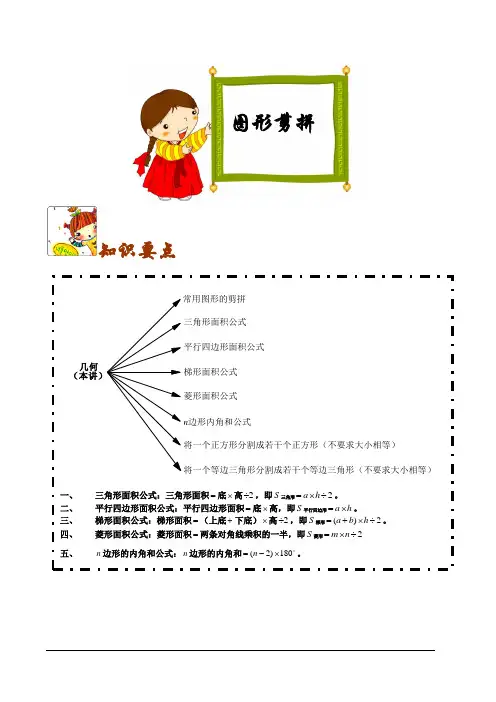
知识要点图形剪拼菱形面积公式将一个等边三角形分割成若干个等边三角形（不要求大小相等）将一个正方形分割成若干个正方形（不要求大小相等）n 边形内角和公式常用图形的剪拼梯形面积公式平行四边形面积公式三角形面积公式 几何（本讲）一、 三角形面积公式：三角形面积=底⨯高2÷，即S 三角形2a h =⨯÷。

二、 平行四边形面积公式：平行四边形面积=底⨯高，即S 平行四边形a h =⨯。

三、 梯形面积公式：梯形面积=（上底+下底）⨯高2÷，即S 梯形()2a b h =+⨯÷。

四、 菱形面积公式：菱形面积=两条对角线乘积的一半，即S 菱形2m n =⨯÷ 五、n 边形的内角和公式：n 边形的内角和(2)180n =-⨯o 。

图形面积【例 1】如图所示，已知三角形的一条边为a，这条边上的高为h。

请用图形剪拼的方法，求出这个三角形的面积S三角形。

hahaha【例 2】如图所示，已知平行四边形的一条边为a，这条边上的高位h。

请用图形剪拼的方法，求出这个平行四边形的面积S平行四边形。

ha【例 3】如图所示，已知梯形的两条平行的边分别为a、b，梯形的高为h。

请用图形剪拼的方法，求出这个梯形的面积S梯形。

hab【例 4】如图所示，已知菱形的两条对角线分别为m、n。

请用图形剪拼的方法，求出这个平行四边形的面积S菱形。

（提示：菱形的两条对角线相互垂直）mn图形分割【例 5】 （2005年12月第六届“中环杯”小学生思维能力训练活动四年级复赛第二（5）题）将一个长方形分成形状完全一样的四块，至少画出8种分法，请用图表示。

（形状一样，排列方向不一样，只能看作一种分法）【例 6】 如图所示为一个34⨯的长方形方格纸，请用5种不同的方法将它分割成完全相同的两部分（保持每个小方格的完整）。

【例 7】 如图所示，请将44⨯的正方形分成形状相同、大小相等的四个图形，并且使其中每个图形都含有“上海世博”这四个字。

备课说明：1、本讲分为两部分，第一部分为应用题（1小时），共10道题，题目类型较多，其中1复习了上堂课学习的还原问题，可让学生自行完成；5、6为和差倍基础题，为下节课的和差倍问题做准备；10为第一期周长与面积拓展提高中的难题，利用割补思想解题，可先让学生思考，再进行讲解。

第二部分为盈亏问题（11小时），共3道例题和练习。

其中例1为基础题，例题3小题，练习3小题，介绍了盈亏问题的3种类型，用时25分钟左右，要求学生熟练掌握并会判断盈亏问题的三种类型，明确盈亏问题中每次分配的总量与参与分配对象是不变的；例2（15分钟）、例3（15分钟）为盈亏问题的提高题，让学生学会判断什么是分配对象，什么是物品，并能找出盈数与亏数，再通过对比的思想，解决问题。

2、重点：学会分析并解决应用题；能准确找出盈数与亏数，通过对比的思想解决盈亏问题。

难点：能准确找出盈数与亏数，通过对比的思想解决盈亏问题。

解答应用题的一般步骤：弄清题意，找出已知条件和所求问题；分析题里数量间的关系，确定先算什么，再算什么，……最后算什么；列出算式并解答；检验，写答句。

小明家养了一些鸭子，要知有多少，细细想一想：“鸭子一半下了水，一半的一半正往水里走，剩下15只围在小明身边吃食物。

”一共有多少只鸭？解：602215=⨯⨯（只）答：一共有60只。

一筐梨连筐重40千克，卖掉一半后，连筐重22千克，筐重多少千克？解：42)2240(40=⨯--（千克）答：筐重4千克。

一只油桶里有一些油，如果把油加到原来的2倍，油桶连油重26千克；如果把油加到原来的4倍，这时油和桶共重48千克，原来油桶里有油多少千克？桶有多少千克？ 解：油重 ()()()kg 11242648=-÷-桶重 ()kg 421126=⨯-答：原来油桶里有油11千克，桶有4千克。

甲、乙、丙三个公司到汽车制造厂订购了18辆汽车，按合同三个公司平均分配，付款时丙没有带钱，甲公司付出10辆的钱，乙公司付出8辆的钱，丙公司应付款90万元。

行程必考题型综合一、行程必考题型综合例1已知甲乙两人相距100米。

甲每秒步行3米，乙每秒步行2米。

⑴两人相向而行，经过多少秒相遇？⑵两人同向而行，乙在前，甲在后，经过多少秒相遇？⑶两人相向而行，且甲带了一只狗和他同时出发。

狗以每秒5米的速度奔向乙，碰到乙后再奔向甲，碰到甲后再奔向乙，直到两人相遇才停下。

两人相遇时狗共跑了多少米？⑷两人同向而行，乙在前，甲在后，甲追上乙时，狗共跑了多少米？⑸两人同向而行，乙在前，甲在后，甲要在10秒内追上乙，速度应提高到多少米/秒？例2A、B两地同时出发，匀速相向而行，第一次相遇时离A地150千米。

两车继续各自前行，分别到达B、A两地后立刻返回，不作停留，在离A地70千米处第二次相遇。

AB两地相距( )千米？例3下图为一圆形跑道，甲从A点出发，乙从B点出发，都按顺时针方向跑。

A、B正好在圆的一条直径上，圆周长为20米，甲每秒跑4米，乙每秒跑3米，则当甲第一次追上乙时，甲跑了( )圈。

考点分析：环形跑道追及问题例48km/时，逆流而上7km/时。

两船同时同地出发，甲顺流而下，乙逆流而上，各自到达终点后返回。

经过2小时两船同时回到出发点。

那么在这2小时内两船航行方向相同的时间有多少小时？考点分析：比例行程问题90千米/小时，乙车速度为60千米/小时。

甲乙两车分别从AB两地同时出发相向而行，在途径C地时，乙车比甲早到10分钟；第二天甲乙两车分别从BA两地同时返回出发地，在途径C地时甲车比乙车早到1个半小时，那么AB两地相距多少千米？测试题1．甲乙两车，从相距418千米的AB两地同时相对开出，甲车每小时36千米，乙车每小时34千米，开出一小时后甲车发现遗忘物品故返回A地，到达后立即再次向B地开出。

那么甲乙从出发到相遇经过了多少小时？2．(第八届中环杯决赛第七题)在100米赛跑中，小明到达终点时领先小刚10米，这时小王正好跑了81米，如果小刚和小王的速度不变，当小刚到达终点时，小王距离终点还有多远？3．(第九届中环杯四年级决赛动手动脑第四题)在一条公路的沿线有相距100千米的A,B两个城镇.甲，乙两车分别从两城同时开出.已知甲车每小时行70千米，乙车每小时行30千米，且两车出发后不改变行进方向，几小时后两车相距200千米？4．甲乙两人从相距36KM的地方相向而行，如果甲比乙先走2个小时，那么他们在乙出发2.5时后相遇，如果乙比甲先走2个小时，那么他们在甲出发3时后相遇。

解决这类数的平均数的问题的关键在于弄清总和与所对应的个数。

而工作问题中对于复杂的工作效率处理方法：从已知的条件中寻找出工作效率数量关系，把一个复杂的工作效率问题分解成几个简单的问题解决，在还原问题中把最后的结果直接往前推，记住每次操作一定要用单独的式子进行计算，而不能够利用综合算式。

名师点题应用题综合（二）知识概述平均数问题：求若干个数的平均数，就是将个数的总和除以这些数的个数的商，重要公式有：1、平均数=若干个数的总和÷数的个数2、若干个数的总和=数的个数⨯平均数还原问题：有一些应用题的思考，是从应用题所叙述事情的最后结果出发，利用已知条件一步一步倒着推理。

逐步靠拢所求，直到解决问题，这种思考问题的方法，通常我们把他叫做还原法或者倒推法。

工作问题：三个基本的数量：工作时间、工作效率和工作总量工作效率的概念：我们把每小时（每分、每天等）完成的工作量叫做工作效率。

可以得到下面的基本公式： 1、工作效率=工作总量÷工作时间 2、工作时间=工作总量÷工作效率 3、工作总量=工作效率×工作时间羊村有一个长方体的水槽可容水480吨，水槽装有一个进水管和一个排水管。

单开进水管8小时可以把空池注满，单开排水管6小时可把满池水排空，如果装满一池水后，两管齐开需多少小时把满池水排空？ 【解析】根据公式：工作效率=工作总量÷工作时间所以，进水的速度：480÷8=60吨/小时 排水的速度：480÷6=80吨/小时那么排水管在排出进水管进的水的同时，每小时排出80-60=20吨水，所以两管齐开，实际的工作效率就是排出水20吨/小时。

因为总量是不变的，是480吨，所以工作时间=工作总量÷工作效率=480÷20=24小时。

阿奇参加射击比赛，他一共打了10枪，每枪都射中靶子，位置如图中的“⨯”所示。

图中数字表示击中靶 子各部位能得到的分数。

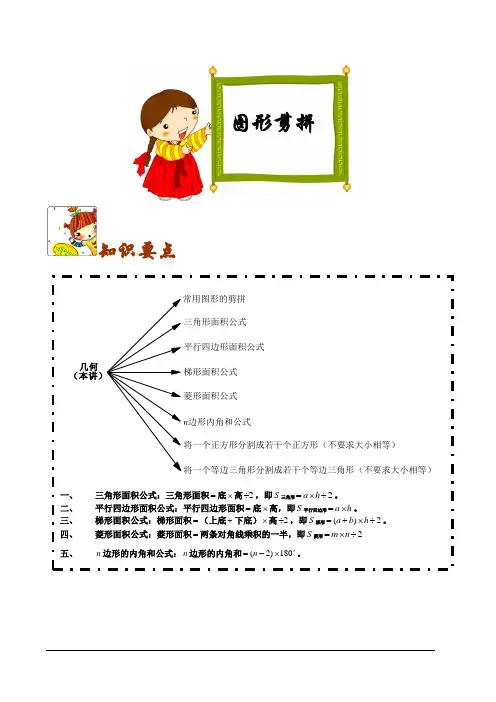
知识要点图形剪拼菱形面积公式将一个等边三角形分割成若干个等边三角形（不要求大小相等）将一个正方形分割成若干个正方形（不要求大小相等）n 边形内角和公式常用图形的剪拼梯形面积公式平行四边形面积公式三角形面积公式 几何（本讲）一、 三角形面积公式：三角形面积=底⨯高2÷，即S 三角形2a h =⨯÷。

二、 平行四边形面积公式：平行四边形面积=底⨯高，即S 平行四边形a h =⨯。

三、 梯形面积公式：梯形面积=（上底+下底）⨯高2÷，即S 梯形()2a b h =+⨯÷。

四、 菱形面积公式：菱形面积=两条对角线乘积的一半，即S 菱形2m n =⨯÷ 五、n 边形的内角和公式：n 边形的内角和(2)180n =-⨯o 。

图形面积【例 1】 如图所示，已知三角形的一条边为a ，这条边上的高为h 。

请用图形剪拼的方法，求出这个三角形的面积S 三角形。

hahaha【分析】当三角形的高在三角形的边上；用两个一摸一样的直角三角形拼在一起，斜边重合，拼成一个长方形。

长方形的长和宽分别是a 和h ，面积S 长方形=a h ⨯；所以直角三角形的面积是长方形的面积的一半，即S 三角形2a h =⨯÷。

当三角形的高在三角形的内部，用两个一摸一样的三角形拼在一起，其中一个沿高剪开，拼成一个长方形。

长方形的长和宽分别是a 和h ，面积S 长方形=a h ⨯；所以三角形的面积是长方形的面积的一半，即S 三角形2a h =⨯÷。

当三角形的高在三角形的外部，三角形的面积等于大直角三角形的面积减去小直角三角形的面积， 即S 三角形(')2'22a a h a h a h =+⨯÷-⨯÷=⨯÷。

所以三角形的面积三角形2a h =⨯÷。

ahaha'ha【例 2】 如图所示，已知平行四边形的一条边为a ，这条边上的高位h 。

2020年中环杯获奖名单（四年级组）准考证号姓名奖项0140010刘奕宏一等奖0140020李青穆一等奖0140031曹家晟一等奖0140034黄琮凯一等奖0140035杨佳选一等奖0140040丁烨颖一等奖0140041姚天成一等奖0140079邓恒煦一等奖0140083于果一等奖0140084徐义卓一等奖0140158楼文颉一等奖0140163杭溢清一等奖0140230周逸明一等奖0140277卞浩宇一等奖0140298江道晟一等奖0140337张亦弛一等奖0140351高麟翔一等奖0140507孙振远一等奖0140625杨镇一等奖0140700许书铭一等奖0140706杨昊一等奖0140734鲍澐鲲一等奖0140791朱子祈一等奖0140798张皓然一等奖0140835张心怡一等奖0140884万宇杰一等奖0140897强蕴祺一等奖0140927谢朋融一等奖0140953周逸桐一等奖0140956戴琤妍一等奖0140959胡彧涵一等奖0140977沈戚榆一等奖0140978王禹听一等奖0141007肖子尧一等奖0141046陈栩越一等奖0141051邵晓玮一等奖0141061毛国皓一等奖0141083邬昱鸿一等奖0141150陈子乐一等奖0141151恽骐源一等奖0141196朱子雍一等奖0141199胡震藩一等奖0141226虞宝丞一等奖0141240沈子轩一等奖0141300孙之昊一等奖0141333杜睿新一等奖0141334陈泓桦一等奖0141356宋志佳一等奖0141392张傲林一等奖0141395李书宇一等奖0540010杨曜堃一等奖0540162李开旭一等奖0540177袁熠晖一等奖1240016樊奕辰一等奖1540007孔玄冰一等奖1640040张一正一等奖1940005郭涵键一等奖2640012刘一陆一等奖。

知识要点逻辑推理根据解题思路的不同，逻辑推理分为两种类型：真假判断型和条件分析型。

真假判断型逻辑推理主要有以下两种推理方法： 1.假设推理法（真假为二选一）：根据已知条件先作一个假设，然后利用已知条件一步一步往下推，直到推出结论为止。

如果从这个假设出发推出自相矛盾的结论，这就说明所作的假设不成立，而假设的反面就一定是成立的。

主要适用于结论只有两种、非真即假的推理题目。

2.枚举排除法（有多种真假情况）：通常直接采用正确的推理，逐一分析，讨论所有可能出现的情况，舍弃不合理的情形，最后得到符合题意的解答。

适用于真假情况不只两种的推理题目。

条件分析型逻辑推理可借助于画图、列表来简化推理过程： 1.图表分析法：将题中关系用图表表示出来，再借助其他分析方法结合图表进行分析推理以得出结论。

其他逻辑推理真假判断型条件分析型枚举排除法假设法图表分析法真假判断型1.甲、乙两人中的一人来自真话村，一个人来自谎话村，谎话村里的人从来不说真话，真话村里的人从来不说谎话。

甲说：“我们两人中至少有一个人在说谎。

”那么甲、乙分别来自什么村呢？2.一个骗子和一个老实人一路同行，骗子总是讲假话，老实人总是讲真话。

请提一个尽量简单的问题，使两人的回答相同。

这个问题可以是什么呢？3.甲、乙、丙三人中只有1人懂法语。

甲说：“我懂。

”乙说：“我不懂。

”丙说：“甲不懂。

”如果三个人的话恰有一句是真话，那么懂法语的是_______，讲真话的是_______。

4.甲、乙、丙三人分别说了下面三句话，请你从他们所说的话判定谁说假话？甲说：“乙在说谎。

”乙说：“丙在说谎。

”丙说：“甲和乙都在说谎。

”5.四个小朋友宝宝、星星、强强和乐乐在院子里踢足球，一阵响声，惊动了正在读书的陆老师，陆老师跑出来查看，发现一块窗户玻璃被打破了。

陆老师问：“是谁打破了玻璃？”宝宝说：“是星星无意打破的。

”星星说：“是乐乐打破的。

”乐乐说：“星星说谎。

”强强说：“反正不是我打破的。

第一讲 数论和计算【例1】 已知248a b 是一个五位数，且是8的倍数，则248a b 最大是（ ），最小是（ ).【解析】 只看末三位，利用去倍数的方法，只需要满足b 能被8整除即可，即a 可以是任意非零的自然数.最大b 是8，最小是0.【例2】 某年的2月有5个星期五，那么这年的1月31日是星期（ ）.【解析】 因为2月最多29天，而如果有5个星期，至少要有29174=+⨯（天），所以，这个2月的第一天和最后一天一定是星期五，即2月1日是星期五，1月31日就是星期四.【例3】 从1开始的100个连续自然数中，将所有既不能被3整除，又不能被5整除的数相加，得到的和是（）.【解析】 利用包含与排除的方法，逆向思考，100以内，能被3整除的数有：99,,9,6,3 ，共33个； 能被5整除的数有：100,,15,10,5 ，共20个；这其中重复的数是：90,75,60,45,30,15，共6个，这样可以算出，能被3或5整除的数之和是：()()241831522020152333313=-÷⨯+⨯+÷⨯+⨯. 所以，题目所求的等于263224185050=-.【例4】 2011年是中国共产党建党90周年.据考证，伟大的中国共产党的确切成立日期是1921年7月23日.2011年的7月23日是星期六，那么从这一天往前，90年前的这一天是星期（ ）.【解析】 考虑90年前，就要考虑过去了多少天.从1922年开始到2011，由22490=+（个）2 （年）可知，共有22个闰年.那么，就一共过去了()2290365+⨯天，我们需要算的是它除以7的余数，根据余数定理，可以分别求出各自除以7的余数后进行简算，算出余数为0，即所有天数和能够被7整除，那么那一天，也仍然和今年的相同，为星期六.【例5】 一个介于800500-之间的三位自然数，正好等于它各位数字和的36倍，则这个自然数是（ ）.【解析】 一个三位数，abc ，则abc ()c b a ++=36，那么说明abc 是9的倍数，那么c b a ++是9的倍数.即9=++c b a 或18或27，因为abc 在800500-中，所以只有18=++c b a 符合要求.abc 6481836=⨯=.【例6】 123123123 （2013个123）13÷的余数是（ ）.【解析】 除数为13，我们知道100111713=⨯⨯，观察与123的关系，发现137111231001123123123⨯⨯⨯=⨯=即2个123就是13的倍数，没有余数，那么2013个123，只需考虑最后一个13123÷的余数即可.6913123 =÷，所以余数为6.【例7】 在325后面补上3个数字，组成一个六位数，使它分别能被5,4,3整除，且使这个数值尽可能小.则这个新六位数是（ ）.【解析】 既能被4整除，又能被5整除，那么个位为0；这个数要尽量小，所以百位为0；能够被3整除的数是数位之和能被3整除，10523=++，再加上2即可被3整除，所以十位为2. 这个六位数是325020.【例8】 100个连续自然数按从小到大的顺序排列，取出其中第1个数、第3个数、第5个数……第99个数，把取出的数相加，得到的结果5400，则100个连续自然数的和为（ ）.【解析】 第1个数比第2个数小1，第3个数比第4个数小 1第99个数比100个数小1，所以所有偶数位数的和比所有奇数位数的和大50，所以100个数的和为108505025400=+⨯.【例9】 已知一个四位数ABCD 满足：+AB CD ABCD ⨯是1111的倍数，则ABCD 的最小值为（ ）.【解析】 (1)当+AB CD=1111ABCD ⨯，因为要求这个数最小，从9,3,2,1 =A 依次尝试，很显然，不成立；(2) 当+AB CD=2222ABCD ⨯，当1=A 时，有1+1B C D =2222B C D⨯，1000++1B CD=2222BCD ⨯，最后有+1B CD=1222BCD ⨯，经分析，B ≠0，有： ①取1=B ,有1+11CD=1222CD ⨯，得：，12CD=1122⨯，+11CD=1122CD ⨯不成立； ②取2=B ,有2+12CD=1222CD ⨯，得：+12CD=1022CD ⨯，13CD=1022⨯不成立； ③取3=B ,有3+13CD=1222CD ⨯，得：+13CD=922CD ⨯，14CD=922⨯，不成立； ④取4=B ,有4+14CD=1222CD ⨯，得：+14CD=822CD ⨯，15CD=922⨯，不成立； ⑤取5=B ,有5+15CD=1222CD ⨯，得：+15CD=722CD ⨯，16CD=922⨯不成立； ⑥取6=B ,有6+16CD=1222CD ⨯，得：+16CD=622CD ⨯，17CD=922⨯，不成立； ⑦取7=B ,有7+17CD=1222CD ⨯，得：+17CD=522CD ⨯，18CD=922⨯，得： CD=29综上，=1729ABCD .【例10】 C B A ,,三人到D 老师家里玩，D 老师给每人发了一顶帽子， 并在每个人的帽子上写了一个四位数.已知这三个四位数都是完全平方数（比如242=，210010=，100,4都是某个数的平方，这样的数称为完全平方数）， 并且这三个四位数的十位数都是0，个位数都不是0.每个小朋友只能看见别人帽子上的数. 这三个小朋友非常聪明而且诚实，发生了如下的对话：A 说：“ C B ,帽子上数的个位数相同.”C B ,同时说：“听了A 的话，我知道自己的数是多少了.”A 说：“听了C B ,的话，我也知道自己的数是多少了，我的这个数的个位数是一个偶数.”求：C B A ,,帽子上的数之和（ ）.【解析】 假设22220()(10)10020ab c mn m n m mn n ==+=++，因为个位都不是0，所以n 不等于0；分析可得，十位数字0是由220mn n +决定的，即：220mn n +的十位数字为0，分析20mn 的十位是偶数，所以2n的十位也是偶数，n 可能的取值有9,8,7,5,3,2,1.(1)当3,2,1=n 时，为了十位为0，需5=m ，有：2512501=、2522704=、2532809= ；(2)当5=n 时，十位不可能为0，不成立；(3)当7=n 时，为了十位为0，需4=m 或9，有：2472209=、2979409=；(4)当8=n 时，为了十位为，0需4=m 或9，有：2482304=、2989604=；(5)当9=n 时，为了十位为0，需4=m 或9，有：2492401=、2999801=； 综上，得到9个满足条件的数，按照个位数的数字将其分为三组：()()()9801,2401,2501,9604,2304,2704,9409,2809,2209 ，根据第三句话，个位是偶数，所以这三个数就是()9604,2304,2704，求和14612960423042704=++.【例11】=÷+÷30003303630331000120112012（ ）. 【解析】 原式10001101210111000120112012÷+÷=()3023100011000130231000130233023100011012101120112012=÷⨯=÷=÷+=【例12】=÷+⨯÷175********（ ）. 【解析】175********÷+⨯÷ ()()61710217594317591743175913131743175913131743=÷=÷+=÷+÷=÷+⨯÷÷=÷+⨯⨯÷=【例13】20122011201020092008200720062005876543--++--+-+--++-= （ ）.【解析】 可以发现，以4个数为一组运算，例02009201020112012=+--20123-有()132012+-即2010项，50242010=÷（组）2 （个数），即剩下134=-，所以答案为1.【例14】=⨯÷20185185999999（ ）.【解析】 看到“185185”，想到重复数组，那么可想到把“999999”也看做重复数组.201000185100199920185185999999⨯÷÷⨯=⨯÷ 20185999⨯÷= 观察数字的关系，999与185中都有37108205373727=⨯÷÷⨯=【例15】 75 4.7+15.925=⨯⨯（ ）【解析】 原式325 4.715.925253 4.715.92514.115.92530750=⨯⨯+⨯=⨯⨯+=⨯+=⨯=（）（）备选题：【例16】 用七个数字1~7组成三个两位数、一个一位数；这四个数的各个数位上的数字都不相同，并且四数之和等于100.请问：最大的两位数可能是多少？ 【解析】 设四个数分别是ab 、cd 、ef 、g ；则()()10100ab cd ef g a c e b d f g +++=++++++=，b d f g +++应是10的倍数；而1728++= ：当10b d f g +++=时，18a c e ++=，和是190，不满足；当20b d f g +++=时，8125a c e ++==++，最大两位数是57. 【例17】 abc 是一个质数，那么abcabc 的约数共有多少个？【解析】100171113abcabc abc abc =⨯=⨯⨯⨯， 所以共有(11)(11)(11)(11)16+⨯+⨯+⨯+=个.【例18】 两个数的最大公约数是16，最小公倍数是96，这两数和最小是多少？【解析】 设两数为16a ，16b ，（a b <）且(,)1a b =，则可得1696ab =，也即6ab =，故1,6a b ==或2,3a b ==，代入比较可知和最小为80.【例19】 已知m n 、两个数都是只含质因数3和5，它们的最大公约数是75，已知m 有12个约数，n 有10个约数，求数m 与n 的和．【解析】 因为27535=⨯，所以我们如果设35p q m =⨯，35x y n =⨯，那么p x 、中较小的数是1，q y 、中较小的数是2．我们知道一个数的约数的个数等于它分解质因数后每个质因数的质数加1的乘积．所以(1)(1)12,(1p q x y +⨯+=+⨯+=, 又123426=⨯=⨯，1025=⨯，不难得出3,2,1,4p q x y ====.所以3235m =⨯，435n =⨯，=2550m n +.。