北航张量讲义5
- 格式:doc
- 大小:567.50 KB
- 文档页数:11
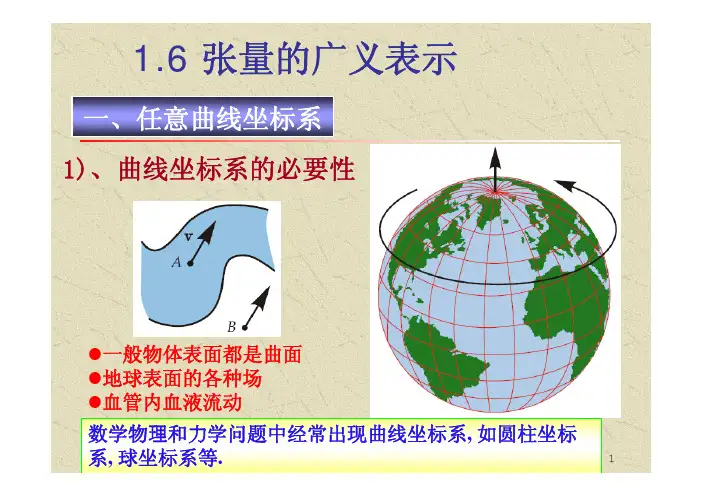
1.6 张量的广义表示一、任意曲线坐标系1)、曲线坐标系的必要性z一般物体表面都是曲面z地球表面的各种场z血管内血液流动数学物理和力学问题中经常出现曲线坐标系, 如圆柱坐标2)、曲线坐标系与笛卡尔直角坐标系的区别a)、当地性9笛卡尔直角坐标系的单位基矢量在整个欧氏空间中任何位置都不改变大小和方向;9而曲线坐标系中坐标方向是改变的,曲线坐标线的方向只能是指曲线坐标线上某点处曲线的切线方向;9任意曲线坐标系是由无数个附于空间个点的小斜交直线坐标系(只用来描述空间一点及其无穷小的一个邻域里的坐标空间性质)集合而成。
《张量算法》,吕盘明,中科大出版社b)、斜交性9笛卡尔直角坐标系的单位基矢量都正交,两个基矢量的叉积很容易用第三个基矢量表示;9而斜交坐标系中由于基矢量不互相垂直,上述问题就麻烦了,这启发我们再定义一组基矢量——对偶基矢量。
二、曲线坐标系的基矢量在曲线坐标系中,空间一点P 的位置矢量r 是曲线坐标x i 的函数,则:ii dxxd ∂∂=r r 空间一点P 的位置矢量可用直角坐标z i 表示为:jj z i=r 式中i j 为沿坐标轴z j 方向的单位矢量。
j i ji jj ixz x z z x i ∂∂=∂∂∂∂=∂∂r r 上式表明,是单位矢量i j 的线性组合,因此也是矢量。
ix ∂∂r注意j j zi =∂∂r表征当x i 变化时位置矢量r 的变化,因此的方向是沿坐标曲线x i 的切线方向。
矢量可以取作曲线坐标系的基矢量(协变基矢量):i x ∂∂r i x∂∂r i x∂∂r ji ji i xz x i r g ∂∂=∂∂=特点:①对于在曲线坐标系中的每一点,都有三个基矢量。
②基矢量一般不是单位矢量,彼此也不正交;作用在一点的任意矢量V ,可以沿g i 的方向按平行四边形法则分解:jjv g =V ③基矢量可以有量纲,但一点的三个基矢量的量纲可以不同;④基矢量不是常矢量,它们的大小和方向依赖于它们所在点的坐标。






第五章 张量分析§5.1 张量函数及其导数一、张量函数、同向同性张量函数的定义若一个张量H(标量、矢量、张量)依赖于n 个张量1T 、2T 、……、n T (矢量、张量)而变化,即当1T 、2T 、……、n T 给定时,H可以对应的确定(或者说,在任意坐标系中,H的每个分量都是1T 、2T 、…、n T 的一切分量的函数),则称H 是张量1T 、2T 、……、n T 的张量函数,记作:12H ()n F T T T =、、…、 (1) 如应力、应变关系 ():F C σεε==kl ij ijkl C σσ=定义:矢量的标是函数()f u ϕ=,如将自变量u 改为 uQ U =∙(Q 为任意正交张量),函数值保持不变,则称此标量函数为各向同性标量函数。
定义张量X 的旋转量X : 1)若X ϕ=为标量,则 X ϕϕ== (2) 2)若X u =为失量,则 T X u Q U u Q==∙=∙ (3) 3)若X T =为二阶张量,则X T =为T 的正交相似张量 T X TQ T Q ==∙∙ (4) Q 为一任意正交张量(可表示旋转与反射)。
定义:一函数12()n x f X X X = 、、…、,当将自变量12n X X X、、…、改为其旋转量 12n X X X 、、…、时,函数值x 必相应地变为其旋转量 x,即: 12()n x f X X X = 、、…、⇒ 12()nx f X X X=、、…、 对任意的Q则的此函数为各向同性函数。
二、张量函数导数的定义,链规则1. 有限微分,导数与微分定义标量x 的函数()F x 对于增量z 的有限微分'()j F x z 为'01()lim [()()]j h F x z F x hz F x h→=+- (5)z 是自变量x 的有限量值的增量,与x 的量纲相同,h 是一个无量纲的无穷小量。
对矢量v 的矢量函数w,即()w F v =(6)定义:'01()lim [()()]j h F v u F v hu F v h→=+- (7)'(;)F v u 也是一个矢量,而且有''()()j F v u F v u =∙ (8)'()F v 是一个二阶张量,称为函数()F v 的导数,或写作()dF v dv又 ()()'(;)()'()()F v hu F v hF v u o h hF v u o h +-=+=∙+(9)其中 ()o h : 0()lim 0h o h h→= (10)令 dv hu = ,取(10)式的主部,称为()F v的微分,它是当自变量v 有微小的增量dv 时,函数F 的微小增量,记作dF ,'()['()]TdF F v dv dv F v =∙=∙ (11)下面给出n 阶张量A 的m 阶张量函数()T A导数的一般定义,01'()lim [()()]j h T A C T A hC T A h→=+-(12)增量C 是与自变量A 同价的n 阶张量,而有限微分'(;)T A C 是与函数()T A同价的m 阶张量。

第二章晶体性质的数学描述研究内容张量的概念二阶张量-重点介绍-推导变换关系 二阶张量示性曲面及主轴化高阶张量及其变换三阶张量四阶张量晶体宏观对称性与晶体张量的关系张量的概念标量物理中常见的一些量,如密度、温度等等很多。
特点:无方向可用一个数值完全表示矢量区别于标量的另一类物理量,既有数值又有方向,如机械力就是矢量。
矢量用黑体字母表示,如F 。
在直角坐标系中用矢量在该坐标系上的分量表示矢量。
例如电场强度矢量E 记为:123[,,]T E E E =E 123E E E ++E=i j k二阶张量张量的概念以电场强度和极化强度矢量为例:123P P P =++P i j k 123E E E ++E=i j k对于各向同性晶体中,同方向则,P E0εχ=P E123[,,]T E E E =E 123[,,]T P P P =P¾如果在各向异性晶体中情况就复杂了,电场强度和它引起的极化强度的方向一般不相同¾这时电场强度的每个分量对极化强度每个方向的分量均有影响,且影响的程度不同,这时我们就不能简单的利用前面的公式()11112130111122133()()()P P E P E P E E E E εχχχ=++=++()22122230211222233()()()P P E P E P E E E E εχχχ=++=++()33132330311322333()()()P P E P E P E E E E εχχχ=++=++张量的概念我们把上述公式表示为矩阵的形式1112131120212223233313233P E P E P E χχχεχχχχχχ⎛⎞⎛⎞⎛⎞⎜⎟⎜⎟⎜⎟=⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎝⎠⎝⎠⎝⎠ 1、P 的每一个分量与电场强度的三个分量存在线性关系2、坐标系确定后为常数3、各向异性介质的电极化特性需用9各数值才能完整描述----我们接下来会详细介绍ij χ张量的概念-二阶张量111213212223313233χχχχχχχχχ⎛⎞⎜⎟⎜⎟⎜⎟⎝⎠我们称这个3×3的矩阵为二阶张量张量的概念-二阶张量推广-如果某个物理性质T ,可以表征另外两个物理量p,q 之间的关联,并具有如下关系111213112212223233313233T T T P q P T T T q P q T T T ⎛⎞⎛⎞⎛⎞⎜⎟⎜⎟⎜⎟=⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎝⎠⎝⎠⎝⎠ 我们称构成二阶张量ij T 张量的概念-二阶张量张量的习惯写法:引入爱因斯坦求和法则-略去求和符号31(1,2,3)i ij j j p T q i ===∑i ij j p T q =i 为自由下标,j 为求和下标,注意顺序1、下标符号任意选定,但要有区别2、自由下标前后呼应,求和下标成对出现张量的概念-二阶张量张量的概念-二阶张量或者表示为矩阵的形式:P Tq=对于我们晶体光学范畴研究的二阶张量均有:ij ji T T =对称张量T T ′=张量的概念-二阶张量我们可以将二阶张量的下标作如下简化:11-1 22-2 33-323 32-4 13 31-5 12 21-6121112131653212223624431323354356T T T T T T T T T T T T T T T T T T T T T T T T ⎛⎞⎜⎟⎜⎟⎛⎞⎛⎞⎜⎟⎜⎟⎜⎟⇒⇒⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎝⎠⎝⎠⎜⎟⎜⎟⎜⎟⎝⎠张量的概念9标量(零阶张量)9矢量(一阶张量)9二阶张量9三阶张量9四阶张量。

附录1 各向同性张量分量的构成通常有两种求各向同性张量分量表达式的方法。
一是利用某些特殊的坐标变换,根据各向同性张量定义直接求出分量表达式;二是利用线性张量函数和各向同性张量函数的Chauchy 表示定理求分量表达式。
前者较为直观,阶数升高时比较麻烦,后者较为抽象,但适用于任意阶张量。
附1.1 用特殊坐标变换求各向同性张量分量表达式根据定义,各向同性张量为在任意直角坐标系下分量值不变的非零张量,如ij ij ijkijk A A A A ''==♣ 一阶张量一阶张量满足i ij j i i i a a a a a '==++112233ββββ考虑附图1特殊坐标变换根据各向同性张量定义和变换II (附图1b )()()()a =a a a a a =a a a =a a =a a a a '==+='==+'==+=111222222233333331111111βββ(1.1a ) a =a a =123 (1.1b )根据变换I (附图1a )()a =a a a a a '==-=-=1111111110βa =a a ==1230这表明★ 不存在一阶各向同性张量从(1.1)式的推导过程可归纳下面的轮换定理:将各向同性张量分量指标作置换 122331,,所得的分量值不变。
例如A =A =A A =A A A =A =A =112233122331213213♣ 二阶张量根据变换I (附图1a )()2A =A =A A A '=-=111111111111111ββ()()()()A =A =A A A A A =A =A A A A '=-+=-='=+-=-=12121122121212122121221121122121110110ββββ再由轮换定理A =A =A =A =A A A =A =A ===1122331223312132130λ所以有ij ij A =λδ这是二阶各向同性张量分量的一般形式。
♣ 三阶张量根据变换I (附图1a )()A =A =A A A A '=-=-=311111111111111111111111110βββ不难得知,指标中有两个2,一个1或两个3,一个1或三个指标均不同的分量也有同样结果A A =A A A =A A =A =A A =A =A ======13331333112221222112323131213221332100再由轮换定理A =A =A A =A A A =A A A =A A A =A A A =A A A =A A =============11122233311222333112123231321132213311322133213121232331112223300000至此27个分量全为零,表明★ 不存在三阶各向同性张量♣ 四阶张量第一,考虑4个指标相同的分量(共3个) 根据变换I (附图1a )()A =A =A A A '=-=411111111111111111111111111111ββββ 由轮换定理A =A =A =111122223333η (1.2)第二,考虑3个指标相同的分量(共24个) 根据变换I (附图1a )()()A =A =A A A A '=-+=-=311121112111111221112111211121112110ββββ不难得知,指标中有三个1一个2或三个1一个3的分量也有同样结果A =A =A A ==11121121121121110 A =A =A A ==11131131131131110再由轮换定理A =A A A =A A A =A A A =A A A =A A A =A A A =A A A =A A ================1112222333311121223233131211232231332111322213331113222133321131221233231311212232333111122223330000000所以有3个指标相同的分量全为0。
第三,考虑2个指标相同另两个不同的分量(共36个)根据变换I (附图1a )()()()A =A =A A A A '=+-+=-=2331233123333112233123312331233121110ββββ不难得知,指标中有两个3,或两个2的分量也有同样结果A =A =A ==331233211323012个...() A =A =A ==223122133212012个...()再由轮换定理A =A =A ==112311322131012个...()36个分量全为0。
第四,考虑指标中有两对重复的分量(共18个) 根据变换I (附图1a )()()A =A A A '=-+=211221111222211221122112211ββββ 类似A =A A =A ''1212121221122112 根据附图2变换III 可证1,2指标可交换()()22A =A =A A '=++11221122121221************ββββ 同理A =A A =A 1212212112212112再由轮换定理A =A =A =A =A =A A =A =A =A =A =A =A =A =A =A =A =A ==112222112233332233111133121221212323323231311313211212213223233213313113λμγ至此81个分量全部确定,归纳为1.3)()()()()()()()()A I I I I I I ik jk ik jk T T T ijk ij k ij kij kT T TA =++=++λδδμδδγδδλμγ上式虽然未出现(1.2)式的η,但实际上包括了 i =j =k =的情况,由(1.2)式和(1.3)式得=++ηλμγ可见η不是独立参数。
(1.3)式是四阶各向同性张量分量的一般形式。
从以上讨论可知,奇数阶张量不是各向同性张量,这是否为普遍规律?另外当阶数进一步升高,用上面方法构造各向同性张量非常困难。
附1.2 用线性张量函数和Chauchy 表示定理求分量表达式♣ 各向同性张量函数与Chauchy 表示定理自变量为张量的函数称张量函数,其函数值可以是标量,也可以是张量,例:A ui ij j ==A u v v (1.4)u 、 v 为向量,A 为二阶张量。
当A 为固定值,u 为变量时,v 为u 的张量函数,函数关系为,()()f A =,(1.4)式记为 ()f u =v (1.5)f A 或亦称为变换或映射,它把一向量变换为另一向量(见附图3a )。
如果某变换Q u =v (1.6)保持任意两个向量的点积不变,则称为正交变换。
我们知道,点积决定向量的长度和夹角,因此,在正交变换下,向量的长度与向量之间的夹角不变(见附图3b )。
★ 这里的正交变换是同一坐标系的变换,定义卡氏张量的正交变换是不同坐标系间的变换因为()()Q u Q u i i ki k j i j ==Q Q u u ↔12121212v v v v若点积不变,必有T Q Q I ki k j i jQ Q δ==↔(1.7)u u i i ij i j i i=δu u u u ==↔1212121212v v v v(1.7)式为正交变换的充要条件,也可作为正交变换的定义。
满足(1.7)式的张量称为正交张量。
由此可见★ 正交变换具有保点积性,反之保点积性的变换必为正交变换再讨论一种有重要应用的张量函数,即自变量为向量组,函数为标量的张量函数:()u u u m φ=f ,,...,12(1.8)例如【双点积】⇨A a b ij i j φ==A a b : (1.9a )【四重点积】⇨A φ=┋a b c d ijk i j k =A a b c d(1.9b )附图3uy 1(a ) 正交变换保持长度和夹角不变向量的变换y 2()f u =v 向量变换的图示 y 1y 21v (b ) u 1θθ2v u 2当式中二阶或四阶张量A 取固定值时,上式为向量的标量函数()a b φ=f ,(1.10a ) ()a b c d φ=f ,,,(1.10b )若对任一自变量(例如b )满足()()()a b b a b a b φ=f αβαf βf ''+=+,,,(1.11)则称为线性函数,容易验证(1.9a )式为双线性函数,(1.9b )式为四重线性函数。
一般情况下,函数的函数值将随自变量的变化而变化,例如()()f x y f x y x x y y ≠≠≠11221212,,但对某些函数,自变量的按一定规律变化时,函数值将保持不变,例如 ()x f x y φy ⎛⎫=⎪⎝⎭, 当 x x y y =1212, 有()()x x f x y φφf x y y y ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭12112212,,(x x y y ≠≠1212)类似地,对于某些张量函数((1.8)式),自变量按正交变换((1.6)式)变化时函数值将保持不变,这类函数称为各向同性标量函数:()()u u u Q u Q u Q u m m f ,,...,f ,,...,=1212(1.12)对于各向同性标量函数,有著名的Chauchy 表示定理: 标量函数为各向同性的充要条件为函数可表示为自变量点积的函数:()()u u u u u m i j f ,,...,φi,j m ==121,...,(1.13)也就是自变量若保点积变化u u i j i ji,j m ==1,...,v v (1.14)函数值将保持不变,()()()()u u u u u m i j i j m f ,,...,φφ=f ,,...,==1212v v v v v (1.15)(1.14)、(1.15)式可作为(1.13)式的等价描述证明:① 充分性利用正交变换保点积特性得()()()()()()u u u u u Q u Q u Qu Q u Q u m i j i j m f ,,...,φφ=f ,,...,==1212充分性得证。
② 必要性需证明当(1.12)式成立时(1.13)式成立,而(1.13)式成立等价于在(1.14)式条件下,(1.15)式成立。
先证明在保点积条件下,存在正交变换,使得Q u i i=i m =1,...,v (1.16)因为自变量的取值是相互独立的,故在三维欧氏空间中,有3个自变量线性无关(m=2时为2个),不妨设u u u ,,123线性无关,几何上表示三向量不共面。