下载文档原格式
一 爱因斯坦求和约定1.1指标变量的集合：n n y y y x x x ,...,,,...,,2121表示为：n j y n i x j i ...,3,2,1,,...,3,2,1,==写在字符右下角的 指标，例如xi 中的i 称为下标。
写在字符右上角的指标，例如yj 中的j 称为上标；使用上标或下标的涵义是不同的。
用作下标或上标的拉丁字母或希腊字母，除非作了说明，一般取从1到n 的所有整数，其中n 称为指标的范围。
1.2求和约定若在一项中，同一个指标字母在上标和下标中重复出现，则表示要对这个指标遍历其范围1，2，3，…n 求和。
这是一个约定，称为求和约定。
例如：333323213123232221211313212111bx A x A x A b x A x A x A bx A x A x A =++=++=++筒写为：ijijbx A =ｊ——哑指标ｉ——自由指标，在每一项中只出现一次，一个公式中必须相同遍历指标的范围求和的重复指标称为“哑标”或“伪标”。
不求和的指标称为自由指标。
1.3 Kronecker-δ符号（克罗内克符号）和置换符号Kronecker-δ符号定义j i ji ij ji ≠=⎩⎨⎧==当当01δδ置换符号ijkijk e e =定义为:⎪⎩⎪⎨⎧-==的任意二个指标任意k j,i,当021)(213,132,3的奇置换3，2，1是k j,i,当112)(123,231,3的偶置换3，2，1是k j,i,当1ijk ijke ei,j,k 的这些排列分别叫做循环排列、逆循环排列和非循环排列。
置换符号主要可用来展开三阶行列式：231231331221233211231231133221332211333231232221131211a a a a a a a a a a a a a a a a a a a a a a a a a a a a ---++==因此有：ijmjimii i i jijAA aa a a a ==++=δδδδδ332211kijjkiijkkjiikjjikijkee e e e e e ==-=-=-=同时有：ijjijij iiiijijijkj ikilkljkijjjiiijijijkjikiie e aa aa a a a aa δδδδδδδδδδδδδδδδδδδ=⋅=++=========++=332211332211331001010100131211232221333231321333222111321321321-=====δδδδδδδδδδδδδδδδδδδδδδδδδδδe e k j i k j i k j i k k k j j j i i i ijk333222111321321321r q p r q p r q p k k k j j j i i i pqr ijke e δδδδδδδδδδδδδδδδδδ⋅=ipp i p i p i p i δδδδδδδδδ==++11332211krkqkpjrjqjpiriqippqrijke e δδδδδδδδδ=jqirjriqjrjqiriqkqrijke e kp δδδδδδδδ-===321321322311332112312213322113312312332211333231232221131211k j i ijkkjiijkaa a e a a a e aa a a a a a a a a a a a a a a a a aaaa a aaa a A ==---++==Kronecker-δ和置换符号符号的关系为：itjsjtiskstkije e δδδδ-=二 张量代数2.1张量的加法(减法)两个同阶、同变异(结构) 的张量可以相加(或相减)。
§1 张量的定义张量：在三维笛卡儿（Descartes）坐标系中，一个含有三个与坐标相关的独立变量集合，通常可以用一个下标表示。
例如，对于位移分量u，v，w可以表示为u1,u2,u3，缩写记为u i，i=1, 2, 3。
对于坐标x,y, z可以表示为x i。
对于一个含有九个独立变量的集合，可以用两个下标来表示。
例如九个应力分量或应变分量（由于对称，实际独立的仅有六个）可以分别表示为σij和εij，其中σ11 , σ22分别表示σx, σxy（就是τxy)；ε11 , ε22分别表示εx,εxy(）等。
同样，一个含有27个独立变量的集合可以用三个下标表示；而含有81个独立变量的集合可以用四个下标表示，依次可以类推。
为了给张量一个确切的定义，首先讨论矢量定义。
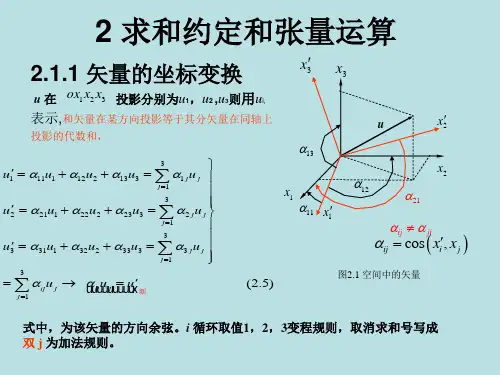
在坐标系Ox1x2x3中。
矢量OP的三个分量ζ 1， ζ 2，ζ3可以缩写作ζ i，同一矢量OP在新坐标系Ox'1x'2x'3中，写作ζ '1，ζ '2，ζ '3，缩写为ζ'i。
设坐标系Ox1x2x3与Ox'1x'2x'3的夹角方向余弦如下表所示方向余弦n i'j的第一下标对应于新坐标轴，而第二下标对应于原坐标轴。
则矢量在新老坐标系中的关系为或者上式可以缩写为或者。
a2, a3)和OP(ζ1, ζ2, ζ3)，作它们的标量积，则考察矢量A(a1,显然，此标量积与坐标轴的选取无关，如果上述矢量作坐标变换，则反之，如ζ ' 为已知矢量，而a i为与坐标有关的三个标量，使一次形式在坐标变换时保持不变。
根据矢量定义，则a i 也是矢量。
推广上述的命题，可以给张量一个解析的定义。
设(ζ 1, ζ 2, ζ3)和(η 1, η 2, η3)是矢量，a ij是与坐标有关的九个量，若当坐标变换时，双一次形式保持不变，则称由两个下标i，j确定的九个量的集合a ij为二阶张量。
爱因斯坦求和约定与张量爱因斯坦求和约定是一个非常重要的数学概念，它能够极大地简化数学公式的书写和推导，特别是与矩阵和张量有关的计算。
在物理学和工程学等应用领域，爱因斯坦求和约定经常被使用。
爱因斯坦求和约定的核心思想是对于一些下标相同的项，它们的和可以用一个简单的符号来表示。
这个符号是希腊字母sigma 上面带一个下标。
比如说，如果有两个向量X和Y，它们的内积可以写成：X·Y = X1Y1 + X2Y2 + X3Y3但是，若干个向量的内积就没法写成这样了。
比如说，如果有三个向量A、B、C，它们的内积就应该是：A·B·C = A1B1C1 + A1B2C2 + A1B3C3 + A2B1C1 + A2B2C2 + A2B3C3 + A3B1C1 + A3B2C2 + A3B3C3这样写起来很麻烦，也不利于推导和计算。
因此，爱因斯坦引入了一个求和约定，使得这个式子可以简化为：A·B·C = Σi,j,k AiBjCk其中，Σi,j,k是指对所有的下标i、j、k都进行求和。
这样，大大简化了运算的复杂程度。
爱因斯坦求和约定的应用不仅仅限于向量的内积，还可以用于张量的计算。
张量是一种类似于矩阵的数学对象，它有多个下标，可以表示多维物理量。
在数学和物理学中，张量经常被用来描述物理系统的运动状态、电磁场、强度等性质。
因此，张量的定义、性质和运算法则都非常重要。
利用爱因斯坦求和约定，可以简化张量的书写和计算。
比如说，如果有一个二阶张量A和一个向量X，它们之间的乘积可以写成：(A·X)i = Σj Aj Xi其中，i和j是张量的两个下标。
这个式子表示的是，将A中第j行的元素和X的第j个元素相乘，然后将所有这样的乘积相加，得到A·X的第i个元素。
同样地，爱因斯坦求和约定也可以用于张量的加法和乘法。
比如说，如果有两个三阶张量A和B，它们的乘积可以写成：(Cijk) = Σl,m,n AilBjmCkn其中，Cijk表示新的三阶张量的第i、j、k个元素，而另外三个下标l、m、n在求和约定中被省略了。
爱因斯坦求和法则引言爱因斯坦求和法则（Einstein summation convention），又称爱因斯坦求和约定，是物理学中一个常用的记号约定。
它简化了向量和矩阵运算的表达方式，使得数学表达更加简洁清晰。
本文将深入探讨爱因斯坦求和法则的原理、应用以及一些注意事项。
爱因斯坦求和法则的定义爱因斯坦求和法则是一种简化向量运算表示的方法，其中通过约定重复指标（上标、下标）的求和。
具体而言，假设有两个张量A和B，它们的下标表示了张量的各个分量。
爱因斯坦求和法则可以将张量的运算表示为如下形式：C i=A ij B j其中i为重复下标，表示对该下标进行求和，j为自由下标，表示不进行求和的下标。
爱因斯坦求和法则的应用向量运算爱因斯坦求和法则在向量运算中的应用非常常见。
考虑一个二维向量a和一个二阶矩阵M，它们的元素如下所示：a=(a1 a2)M=(M11M12 M21M22)根据爱因斯坦求和法则，可以将向量与矩阵的乘法表示为：c i=M ij a j展开求和后，可得到下面两个等式：c1=M11a1+M12a2c2=M21a1+M22a2可以看出，爱因斯坦求和法则简化了向量与矩阵的乘法表示，使得计算更加简洁。
矢量计算在向量运算的基础上，爱因斯坦求和法则还可以应用于矢量的运算。
考虑一个三维矢量v和一个三阶张量T，它们的元素如下所示：v=(v1 v2 v3 )T=(T111T112T113 T121T122T123 T131T132T133)根据爱因斯坦求和法则，可以将矢量与张量的乘法表示为：w k=T ijk v j展开求和后，可得到下面三个等式：w1=T111v1+T112v2+T113v3w2=T121v1+T122v2+T123v3w3=T131v1+T132v2+T133v3爱因斯坦求和法则使得矢量与张量的乘法表示更加紧凑，同时保持了运算的准确性。
注意事项在使用爱因斯坦求和法则时，需要注意以下几点： 1. 重复指标只能出现一次，并且一定要包含一个上标和一个下标。
