合工大数字信号处理习题答案2和3章
- 格式:doc
- 大小:769.57 KB
- 文档页数:17

数字信号处理习题解答 第二章 数据采集技术基础2。
1 有一个理想采样系统,其采样角频率Ωs =6π,采样后经理想低通滤波器H a (j Ω)还原,其中⎪⎩⎪⎨⎧≥Ω<Ω=Ωππ30321)(,,j H a 现有两个输入,x 1(t )=cos2πt ,x 2(t )=cos5πt 。
试问输出信号y 1(t ),y 2(t )有无失真?为什么?分析:要想时域采样后能不失真地还原出原信号,则采样角频率Ωs 必须大于等于信号谱最高角频率Ωh 的2倍,即满足Ωs ≥2Ωh 。
解:已知采样角频率Ωs =6π,则由香农采样定理,可得 因为x 1(t )=cos2πt ,而频谱中最高角频率πππ32621=<=Ωh ,所以y 1(t )无失真;因为x 2(t )=cos5πt ,而频谱中最高角频率πππ32652=>=Ωh ,所以y 2(t )失真。
2.2 设模拟信号x (t )=3cos2000πt +5sin6000πt +10cos12000πt ,求:(1) 该信号的最小采样频率;(2) 若采样频率f s =5000Hz ,其采样后的输出信号; 分析:利用信号的采样定理及采样公式来求解.错误!采样定理采样后信号不失真的条件为:信号的采样频率f s 不小于其最高频率f m 的两倍,即f s ≥2f m○,2采样公式)()()(s nT t nT x t x n x s===解:(1)在模拟信号中含有的频率成分是f 1=1000Hz ,f 2=3000Hz,f 3=6000Hz∴信号的最高频率f m =6000Hz由采样定理f s ≥2f m ,得信号的最小采样频率f s =2f m =12kHz (2)由于采样频率f s =5kHz,则采样后的输出信号⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛====n n n n n n n n n n n f n x nT x t x n x s s nT t s522sin 5512cos 13512cos 10522sin 5512cos 35112cos 105212sin 5512cos 3562cos 10532sin 5512cos 3)()()(πππππππππππ 说明:由上式可见,采样后的信号中只出现1kHz 和2kHz 的频率成分,即kHzf f f kHzf f f ss 25000200052150001000512211======,,若由理想内插函数将此采样信号恢复成模拟信号,则恢复后的模拟信号()()t t t f t f t y ππππ4000sin 52000cos 132sin 52cos 13)(21-=-=可见,恢复后的模拟信号y (t ) 不同于原模拟信号x (t ),存在失真,这是由于采样频率不满足采样定理的要求,而产生混叠的结果.第三章 傅里叶分析I. 傅里叶变换概述3。

第二章习题解答1、求下列序列的z 变换()X z ,并标明收敛域,绘出()X z 的零极点图。
(1) 1()()2nu n (2) 1()()4nu n - (3) (0.5)(1)nu n --- (4) (1)n δ+(5) 1()[()(10)]2nu n u n -- (6) ,01na a <<解:(1) 00.5()0.50.5nn n n zZ u n z z ∞-=⎡⎤==⎣⎦-∑,收敛域为0.5z >,零极点图如题1解图(1)。
(2) ()()014()1414n nn n z Z u n z z ∞-=⎡⎤-=-=⎣⎦+∑,收敛域为14z >,零极点图如题1解图(2)。
(3) ()1(0.5)(1)0.50.5nnn n zZ u n z z --=-∞-⎡⎤---=-=⎣⎦+∑,收敛域为0.5z <,零极点图如题1解图(3)。
(4) [](1Z n z δ+=,收敛域为z <∞,零极点图如题1解图(4)。
(5) 由题可知,101010910109(0.5)[()(10)](0.5)()(0.5)(10)0.50.50.50.50.50.5(0.5)n n nZ u n u n Z u n Z u n z z z z z z z z z z z --⎡⎤⎡⎤⎡⎤--=--⎣⎦⎣⎦⎣⎦⋅=-----==--收敛域为0z >,零极点图如题1解图(5)。
(6) 由于()(1)nn n a a u n a u n -=+--那么,111()(1)()()()nn n Z a Z a u n Z a u n z z z a z a z a a z a z a ----⎡⎤⎡⎤⎡⎤=---⎣⎦⎣⎦⎣⎦=----=-- 收敛域为1a z a <<,零极点图如题1解图(6)。
(1) (2) (3)(4) (5) (6)题1解图2、求下列)(z X 的反变换。


部分练习题参考答案第二章2.1 )1(2)(3)1()2(2)(-+++-+=n n n n n x δδδδ)6()4(2)3()2(-+-+-+-+n n n n δδδδ2.2 其卷积过程如下图所示)5(5.0)4()3()2(5.2)1(5)(2)(-------+-+=n n n n n n n y δδδδδδ2.3 (1)3142,73==ωππω这是有理数,因此是周期序列。
周期N =14。
(2)k kp ππ168/12==,k 取任何整数时,p 都不为整数,因此为非周期序列。
(3)k kp k k p 45.02,5126/5221====ππππ,当p 1,p 2 同时为整数时k =5,x (n )为周期序列,周期N =60。
(4)k kp πππ25.16.12==,取k =4,得到p =6,因此是周期序列。
周期N =6。
2.4 (1) ∑∞-∞=-=*=m m n R m Rn h n x n y )()()()()(45(a) 当n <0 时,y (n )=0-0.5 -1 2.55h (m ) x (m ) 00 mm-121 0.51 2 h (0-m)m-121 h (-1-m)m-12 1h (1-m) 0m-121y (n )n-12(b) 当30≤≤n 时,11)(0+==∑=n n y nm(c) 当74≤≤n 时,n n y n m -==∑-=81)(34(d) 当n>7时,y (n )=0所以74307081)(≤≤≤≤><⎪⎩⎪⎨⎧-+=n n n n n n n y 或 (2))2(2)(2)]2()([)(2)(444--=--*=n R n R n n n R n y δδ )]5()4()1()([2-----+=n n n n δδδδ(3)∑∞-∞=--=*=m mn m n u m Rn y n x n y )(5.0)()()()(5∑∞-∞=--=m mnm n u m R )(5.0)(5.05(a) 当n <0 时,y (n )=0(b) 当40≤≤n 时,nn nnm mnn y 5.0221215.05.05.0)(1-=--==+=-∑(c) 当5≥n 时,nnm mnn y 5.03121215.05.05.0)(54⨯=--==∑=-最后写成统一表达式:)5(5.031)()5.02()(5-⨯+-=n u n R n y nn(4)∑∞-∞=-=*=m mn m Rn h n x n y 5.0)()()()(3(a) 当n ≤0 时,y (n )=0(b) 当31≤≤n 时,nnnn m mnn y 5.0121215.05.05.0)(1-=--==∑-=- (c) 当54≤≤n 时,25.05.01621)21(25.05.05.0)(6232-⨯=--==---=-∑nnn nn m mnn y(d) 当n ≥6时,y (n )=0)5(25.0)4(75.0)3(875.0)2(75.0)1(5.0)(-+-+-+-+-=n n n n n n y δδδδδ2.6 (1)非线性、移不变系统(2)线性、移不变系统 (3)线性、移变系统 (4)非线性、移不变系统 (5)线性、移变系统2.7 (1)若∞<)(n g ,则稳定,因果,线性,时变(2)不稳定,0n n ≥时因果,0n n <时非因果,线性,时不变 (3)线性,时变,因果,不稳定 2.8 (1)因果,不稳定(2)因果,稳定(3)因果,稳定 (4)因果,稳定 (5)因果,不稳定 (6)非因果,稳定 (7)因果,稳定 (8)非因果,不稳定 (9)非因果,稳定 (10)因果,稳定2.9 因为系统是因果的,所以0)(,0=<n h n令)()(n n x δ=,)1(5.0)()1(5.0)()(-++-==n x n x n h n h n y 1)1(5.0)0()1(5.0)0(=-++-=x x h h15.05.0)0(5.0)1()0(5.0)1(=+=++=x x h h 5.0)1(5.0)2()1(5.0)2(=++=x x h h25.0)2(5.0)3()2(5.0)3(=++=x x h h 15.0)1(5.0)()1(5.0)(-=-++-=n n x n x n h n h所以系统的单位脉冲响应为)1(5.0)()(1-+=-n u n n h n δ 2.10 (1)初始条件为n <0时,y (n )=0设)()(n n x δ=,输出)(n y 就是)(n h 上式可变为)()1(5.0)(n n h n h δ+-=可得 11)1(5.0)0(=+-=h h 依次迭代求得5.00)0(5.0)1(=+=h h25.00)1(5.0)2(=+=h hnn h n h 5.00)1(5.0)(=+-=故系统的单位脉冲响应为)(5.0)(n u n h n= (2)初始条件为n ≥0时,y (n )=0)]()([2)1(n x n y n y -=-0,0)(≥=n n h2)]0()0([2)1(-=-=-x h h22)]1()1([2)2(-=---=-x h h 32)]2()2([2)3(-=---=-x h hnn h n h 2)1(2)(-=+=所以)1(2)(---=n u n h n2.11 证明(1)因为∑∞-∞=-=*m m n h m x n h n x )()()()(令m n m -=',则)()()'()'()()('n x n h m h m n x n h n x m *=-=*∑∞-∞=(2)利用(1)证明的结果有)]()([)()]()([)(1221n h n h n x n h n h n x **=**∑∞-∞=-*-=m m n h m n hm x )]()()[(12 ∑∑∞-∞=∞-∞=--=m k k m n h k hm x )()()(12交换求和的次序有∑∑∞-∞=∞-∞=--=**k m k m n hm x k h n h n h n x )()()()]()([)(1221∑∞-∞=-*-=k k n h k n x k h)]()()[(12)]()([)(12n h n x n h **=)()]()([21n h n h n x **=(3)∑∞-∞=-+-=+*m m n h m n hm x n h n h n x )]()()[()]()([)(2121∑∑∞-∞=∞-∞=-+-=m m m n hm x m n h m x )()()()(21)()()()(21n h n x n h n x *+*=2.12 ∑∞-∞=--=*=m mn Nm n u am Rn y n x n y )()()()()(∑∞-∞=--=m mNnm n u am Ra)()((a) 当n <0 时,y (n )=0(b) 当10-≤≤N n 时,11/11)/1(1)(11--=--==++=-∑a aa a aaan y n n nnm mn(c) 当N n ≥时,1)/1(1)/1(1)(111--=--==+-+-=-∑a aaa a aaan y N n n NnN m mn最后写成统一表达式:)(1)(11)(111N n u a aa n R a an y N n n N n ---+--=+-++2.13 )]4()([*)()()()(11--=*=n n n u n h n x n y δδ)()4()(4n R n u n u =--=)()()()()(421n u a n R n h n y n y n*=*= )4(1)(113141---+--=-++n u a aan R a an n n2.14 (1)采样间隔为005.0200/1==T)()82sin()(ˆ0nT t nT f t xn a -+=∑∞-∞=δππ)()8100sin(nT t nT n -+=∑∞-∞=δππ (2))85.0sin()(ππ+=n n x数字频率πω5.0=,42=ωπ,周期N =42.15 (1)0)()(0n j n nj j eenn eX ωωωδ-∞-∞=-=-=∑(2)∑∑∞=-+-∞-∞=-==)(0)()(n nj n j n nj j eeen x eX ωωαωω∑∞=--=0)(0n nj eeωωα)(01ωωα---=j ee(3)∑∑∑∞=+-∞=--∞-∞=-===0)(0)()(n nj n nj nn nj j eeeen x eX ωαωαωω)(11ωαj e+--=(4)∑∑∞=--∞-∞=-==00cos )()(n nj nn nj j ne een x eX ωαωωω∑∑∞=----+---∞=-+=+=)()(0][21)(210000n nj j nj j nj nj nj n neeeeeeωωαωωαωωωααωαωαωωωαωωαωω2200)()(cos 21cos 111112100------+----+--=⎥⎦⎤⎢⎣⎡-+-=e e e e e e eeee j j j j j (5)nj N N n n nj j e n N en x eX ωωωπ--=∞-∞=-∑∑⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+==12cos 1)()( ∑∑-=---=-++=1212)(21N Nn nj nNjnNjN Nn nj eeeeωππω⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--+--+--=+-+-+-------)()()()()()(1)1(1)1(211)1(ωπωπωπωπωπωπωωωNj NNj NNj Nj NN j NNj j Nj Nj eeeeee eee-0.92-0.380.920.38x (n ) 0nωωωωωωππωωN jj j j N j eN e eNeN eN 232)123()2cos(cos21cos12sin)2sin(------+--+=2.16 (1)⎰⎰⎰-==--πωπωππωωωπωπωπ2121)(21)(d jed jed eeH n h nj nj nj j⎪⎩⎪⎨⎧=--=为奇数为偶数n n n n nππ20)1(1(2))sin()()()(011n n h n x n y ω=*=)cos()()()(022n n h n x n y ω-=*=2.17 (1))(ωj e X -*(2))]()([21ωωj j eX eX -*+(3))]()([2122ωωjje X eX -+(4))(2ωj eX2.18采样间隔为25.0=T ,采样频率π8=Ωs)(1t y a 没有失真,因为输入信号的频率π21=Ω小于π42=Ωs)(2t y a 失真,因为输入信号频率π52=Ω大于π42=Ωs第三章3.1 设)(ωj eX 和)(ωj eY 分别是)(n x 和)(n y 的傅里叶变换,试求下列序列的傅里叶变换: (1))(0n n x - (2) )(*n x (3) )(n x - (4) )(*)(n y n x (5) )()(n y n x ∙ (6) )(n nx(7) )2(n x (8))(2n x(9)⎩⎨⎧===奇数,偶数n n n x n x 0),2()(9解:(1) FT[)(0n n x -]=∑∞-∞=--n nj enn x ω)(0令0n n n -=',0n n n +'=,则FT[)(0n n x -]=)()(00)(ωωωj n j n n n j eX een x -∞-∞=+''-='∑(2) FT[)(*n x ]=)(*])([)(**ωωωj n nj n nj eX en x en x-∞-∞=-∞-∞=-∑∑==(3) FT[)(n x -]=∑∞-∞=--n nj en x ω)(令n n -=',则FT[)(n x -]=∑∞-∞=''n n j en x ω)()(ωj eX -=(4) FT[)(*)(n y n x ]=)(ωj e X )(ωj e Y证明 )(*)(n y n x =∑∞-∞=-m m n y m x )()(FT[)(*)(n y n x ]=∑∑∞-∞=-∞-∞=-n nj m em n y m x ω)]()([令m n k -=,则FT[)(*)(n y n x ]=mj k kj m eek y m x ωω-∞-∞=-∞-∞=∑∑)]()([=mj k m kj em x ek y ωω-∞-∞=∞-∞=-∑∑)()(=)(ωj eX )(ωj eY(5) FT[)()(n y n x ∙] =∑∞-∞=-n nj en y n x ω)()(=∑⎰∞-∞=-'-''n nj nj j ed eeY n x ωωππωωπ])(21)[(=ωπωωππω'∑⎰∞-∞='---'d en x e Y n nj j )()()(21=ωπωωππω''--'⎰d eX eY j j )()(21)(或者 FT[)()(n y n x ]=)(*)(21ωωπj j e Y eX(6) 因为∑∞-∞=-=n nj j en x e X ωω)()(,对该式两边对ω求导,得到j en nx jd e dX n nj j -=-=∑∞-∞=-ωωω)()(FT[)(n nx ]因此 FT[)(n nx ]=ωωd e dX jj )((7) FT[)2(n x ]=∑∞-∞=-n nj en x ω)2(令n n 2=',则FT[)2(n x ]=∑''-'取偶数n n j en x 2)(ω=nj nn en x n x ω21)]()1()([21-∞-∞=-+∑=])()([212121nj n nj nj n e n x een x ωπω-∞-∞=-∞-∞=∑∑+=)]()([21)21(21πωω-+j j eX eX或者FT[)2(n x ]=)()]()([21212121ωωωj j j eX eX eX =+(8) FT[)(2n x ]=∑∞-∞=-n nj en xω)(2利用(5)题结果,令)()(n y n x =,则FT[)(2n x ]=)(*)(21ωωπj j eX eX =ωπωωππω''--'⎰d eX eX j j )()(21)((9) FT[)(9n x ]=∑∞-∞=-取偶数n n nj en x ω)2( 令∞≤'≤∞-='n n n ,2,则FT[)(9n x ]=)()(22ωωj n n n j eX en x ='∑∞-∞='-取偶数3.2 已知⎩⎨⎧≤<<=πωωωωω||,0||,1)(00j eX求)(ωj e X 的傅里叶反变换)(n x 。

合工大《数字信号处理》习题答案第2章习 题2.4 设系统分别用下面的差分方程描述,)(n x 与)(n y 分别表示系统输入和输出,判断系统是否是线性非时变的。
(1))()(0n n x n y -= (3))sin()()(n n x n y ω=解: (1))()()()()]()([21020121n by n ay n n bx n n ax n bx n ax T +=-+-=+所以是线性系统。
由于)()]([0n n x n x T -= 所以是时不变系统。
(3))()()sin()]()([)]()([212121n by n ay n n bx n ax n bx n ax T +=+=+ω,所以是线性系统。
)()sin()()]([m n y n m n x m n x T -≠-=-ω,所以不是时不变系统。
2.5 给定下述系统的差分方程,试判定系统是否是因果稳定系统,并说明理由。
(1))1()()(++=n x n x n y (3))()(n x e n y =解:(1)该系统是非因果系统,因为n 时刻的输出还和n 时刻以后()1(+n 时间)的输入有关。
如果M n x ≤|)(|,则M n x n x n y 2|)1(||)(||)(|≤++≤,因此系统是稳定系统。
(3)系统是因果系统,因为n 时刻的输出不取决于)(n x 的未来值。
如果M n x ≤|)(|,则M n x n x e e e n y ≤≤≤)|(|)(|||)(|,因此系统是稳定系统。
2.6 以下序列是系统的单位冲激响应)(n h ,试说明该系统是否是因果、稳定的。
(1))(2)(n u n h n= (3))2()(+=n n h δ解:(1)当0<n 时,0)(=n h ,所以系统是因果的。
由于所以系统不稳定。
(3)当0<n 时,0)(≠n h ,所以系统是非因果的。
由于所以系统稳定。
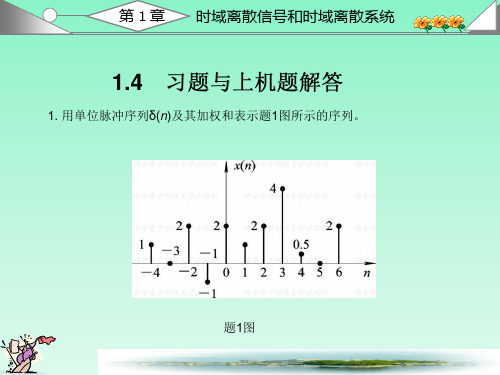
数字信号处理课后答案 1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。
解:()(4)2(2)(1)2()(1)2(2)4(3) 0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号:25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它(1)画出()x n 序列的波形,标上各序列的值; (2)试用延迟单位脉冲序列及其加权和表示()x n 序列; (3)令1()2(2)x n x n =-,试画出1()x n 波形; (4)令2()2(2)x n x n =+,试画出2()x n 波形; (5)令3()2(2)x n x n =-,试画出3()x n 波形。
解:(1)x(n)的波形如题2解图(一)所示。
(2)()3(4)(3)(2)3(1)6() 6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-(3)1()x n 的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图(二)所示。
(4)2()x n 的波形是x(n)的波形左移2位,在乘以2,画出图形如题2解图(三)所示。
(5)画3()x n 时,先画x(-n)的波形,然后再右移2位,3()x n 波形如题2解图(四)所示。
3. 判断下面的序列是否是周期的,若是周期的,确定其周期。
(1)3()cos()78x n A n ππ=-,A 是常数;(2)1()8()j n x n e π-=。
解:(1)3214,73w w ππ==,这是有理数,因此是周期序列,周期是T=14; (2)12,168w wππ==,这是无理数,因此是非周期序列。
5. 设系统分别用下面的差分方程描述,()x n 与()y n 分别表示系统输入和输出,判断系统是否是线性非时变的。
合工大《数字信号处理》习题答案第2章习 题2.1用单位脉冲序列)(n δ及其加权和表示题1图所示的序列。
2.1)1()()1()2(2)4()(-+++-+++=n n n n n n x δδδδδ)6(2)4(5.0)3(4)2(2-+-+-+-+n n n n δδδδ2.2 请画出下列离散信号的波形。
(1))(21n u n⎪⎭⎫⎝⎛(2))()2(n u n - (3))1(21--n u n (4))5()1(---n u n u答案略2.3 判断下面的序列是否是周期的,若是周期的,确定其周期。
(1))873cos()(ππ-=n A n x ,A 是常数;(2))81()(π-=n j e n x 。
2.3 (1)31420=ωπ,所以周期为14。
(2)πωπ1620=,是无理数,所以)(n x 是非周期的。
2.4 设系统分别用下面的差分方程描述,)(n x 与)(n y 分别表示系统输入和输出,判断系统是否是线性非时变的。
(1))()(0n n x n y -= (2))()(2n x n y = (3))sin()()(n n x n y ω= (4))()(n x en y =2.4 (1)由于)()]([0n n x n x T -=)()()]([0m n y n m n x m n x T -=--=-所以是时不变系统。
)()()()()]()([21020121n by n ay n n bx n n ax n bx n ax T +=-+-=+所以是线性系统。
(2))()()]([2m n y m n x m n x T -=-=-,所以是时不变系统。
)()()]()([)]()([2122121n by n ay n bx n ax n bx n ax T +≠+=+,所以是非线性系统。
(3))()sin()()]([m n y n m n x m n x T -≠-=-ω,所以不是时不变系统。
)()()sin()]()([)]()([212121n by n ay n n bx n ax n bx n ax T +=+=+ω,所以是线性系统。
(4))()()]()([21)()()]()([212121n by n ay e e e n bx n ax T n bx n ax n bx n ax +≠==++,所以是非线性系统。
)()]([)(m n y e m n x T m n x -==--,所以是时不变系统。
2.5 给定下述系统的差分方程,试判定系统是否是因果稳定系统,并说明理由。
(1))1()()(++=n x n x n y (2))()(0n n x n y -= (3))()(n x e n y =(4)∑+-==0)()(n n n n k k x n y2.5(1)该系统是非因果系统,因为n 时刻的输出还和n 时刻以后()1(+n 时间)的输入有关。
如果M n x ≤|)(|,则M n x n x n y 2|)1(||)(||)(|≤++≤,因此系统是稳定系统。
(2)当00<n 时,系统是非因果系统,因为n 时刻的输出还和n 时刻以后的输入有关。
当00≥n 时,系统是因果系统。
如果M n x ≤|)(|,则M n y ≤|)(|,因此系统是稳定系统。
(3)系统是因果系统,因为n 时刻的输出不取决于)(n x 的未来值。
如果M n x ≤|)(|,则M n x n x e e e n y ≤≤≤)|(|)(|||)(|,因此系统是稳定系统。
(4)系统是非因果系统,因为n 时刻的输出还和)(n x 的未来值有关。
如果M n x ≤|)(|,则,M nk x n y n n n n k |12||)(||)(|0+≤≤∑+-=因此系统是稳定系统。
2.6 以下序列是系统的单位冲激响应)(n h ,试说明该系统是否是因果、稳定的。
(1))(2)(n u n h n = (2))(2)(n u n h n -= (3))2()(+=n n h δ (4))(1)(2n u n n h =2.6 (1)当0<n 时,0)(=n h ,所以系统是因果的。
由于∞⇒+++=∑∞-∞= 210222|)(|n n h所以系统不稳定。
(2)当0<n 时,0)(≠n h ,所以系统是非因果的。
由于2222|)(|210=+++=--∞-∞=∑ n n h所以系统稳定。
(3)当0<n 时,0)(≠n h ,所以系统是非因果的。
由于1|)(|∑∞-∞==n n h所以系统稳定。
(4)当0<n 时,0)(=n h ,所以系统是因果的。
由于∞⇒+++=∑∞-∞= 222211101|)(|n n h 所以系统不稳定。
2.7设线性时不变系统的单位脉冲响应)(n h 和输入序列)(n x 如题2.7图所示,试求输出)(n y 。
2.7)()]2(5.0)1()(2[)()()(n x n n n n x n h n y *-+-+=*=δδδ)5()4(2)3(5.4)2()1(2)(5.0)1()2(2)2(5.0)1()(2-+-+-+-+-+-+-+-=-+-+=n n n n n n n n n x n x n x δδδδδδδδ2.8 设线性时不变系统的单位冲激响应)(n h 和输入)(n x 分别有以下三种情况,分别求出输出)(n y 。
(1))()(3n R n h =,)()(3n R n x =(2))()(4n R n h =,)2()()(--=n n n x δδ (3))(5.0)(n u n h n=,)()(5n R n x = 2.8(1))()()()()(33n R n R n h n x n y *=*=)4()3(2)2(3)1(2)()]4()3()2([)]3()2()1([)]2()1()([)2()1()()()]2()1()([3333-+-+-+-+=-+-+-+-+-+-+-+-+=-+-+=*-+-+=n n n n n n n n n n n n n n n R n R n R n R n n n δδδδδδδδδδδδδδδδδ(2))()]2()([)()()(4n R n n n h n x n y *--=*=δδ)5()4()1()()]5()4()3()2([)]3()2()1()([)2()(44-----+=-+-+-+---+-+-+=--=n n n n n n n n n n n n n R n R δδδδδδδδδδδδ(3))()(5.0)()()(5n R n u n h n x n y n *=*=)4(5.0)3(5.0)2(5.0)1(5.0)(5.0)]4()3()2()1()([)(5.04321-+-+-+-+=-+-+-+-+*=----n u n u n u n u n u n n n n n n u n n n n nn δδδδδ2.9 确定下列信号的最低采样率与奈奎斯特采样间隔。
(1))100(t S a (2))100(2t S a(3))50()100(t S t S a a +2.9 若要确定奈奎斯特采样间隔,必须先求出信号频谱的最高频率。
(1)抽样函数对应于门函数:)2/()(ωτττa S E t G →,其中τ为门函数的宽度。
由傅立叶变换的对称性知:)(2)2/(ωπτττG t S E a →由题可知,200=τ。
因此,此信号的最高频率是100弧度/秒。
因此,21002∙≥s f π 即,π100=s f ,100π=s T(2)信号为两个抽样函数的乘积,因此频谱应为两个抽样函数频谱的卷积。
由卷积积分的结果来确定信号频谱的范围。
通过上一题目可知,)100(t S a 信号的最高频率为100弧度/秒,因此相卷积后的最高频率是200弧度/秒。
π200=s f ,200π=s T(3)由傅立叶变换的线性,总信号的频谱为两个信号频谱的叠加,然后确定最高频率。
π100=s f ,100π=s T2.10 设系统由下面差分方程描述:)1(21)()1(21)(-++-=n x n x n y n y 设系统是因果的,(1)求该系统的单位脉冲响应。
(2)利用卷积和求输入)()(n u en x nj ω=的响应。
2.10 (1)x(n)=δ(n),因为y(n)=h(n)=0,n<0 所以h(0)=0.5y(-1)+x(0)+0.5x(-1)=1 h(1)=0.5y(0)+x(1)+0.5x(0)=1 h(2)=0.5y(1)+x(2)+0.5x(1)=0.5......h(n)=0.5y(n-1)+x(n)+0.5x(n-1)=0.5n-1 所以 h(n)= 0.5n-1u(n-1)+δ(n)(2)y(n)=x(n)*h(n)= [0.5n-1u(n-1)+δ(n)]* e jwn u(n)= [0.5n-1u(n-1)]* e jwn u(n)+ e jwn u(n)= [e jwn -0.5n ]/ (e jw -0.5)u(n-1)+ e jwn u(n)2.11有一理想抽样系统,抽样频率为π6=Ωs ,经理想低通滤波器)(Ωj H a 还原,其中⎪⎩⎪⎨⎧≥Ω<Ω=Ωππ3||,03||,21)(j H a今有两个输入,t t x a π2cos )(1=,t t x a π5cos )(2=。
输出信号)(1t y a 、)(2t y a 有无失真?为什么?2.11 根据奈奎斯特定理:因为t t x a π2cos )(1=,而频谱中最高角频率2621ππ<=Ωa ,所以)(1t y a 无失真。
因为t t x a π5cos )(2=,而频谱中最高角频率2652ππ>=Ωa ,所以)(2t y a 失真。
2.12 有一连续信号)2cos()(ϕπ+=ft t x a ,式中20=f Hz ,2πϕ=(1) 求出)(t x a 的周期;(2) 用采样间隔s T 02.0=对)(t x a 进行采样,试写出采样信号)(ˆt xa 的表达式。
2.12 (1)s fT a 05.01==(2))()2cos()()()()()(ˆnT t fnT nT t nT xt t x t xn n aT a a -+=-==∑∑∞-∞=∞-∞=δϕπδδ∑∞-∞=-+=n nT t nT )()40cos(δϕπ第3章习 题3.1 求下列序列的z 变换,并标明收敛域。
(1))4()(-=n n x δ(2))(21)(n u n x n⎪⎭⎫⎝⎛=(3))1(21)(--⎪⎭⎫⎝⎛-=n u n x n(4)nn x 1)(=,1≥n (5))1(5.0)(-=n u n x n(6)())(2.0)(n u n n x n=答案: 3.1解(1)由z 变换的定义可知,4)4()(-∞-∞=-=-=∑z zn z X n nδ,0≠z(2)10211121)(21)(--∞=∞-∞=--=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=∑∑z z z n u z X n nn n nn,21||>z(3)n nn n nn z z n u z X -∞--=∞-∞=-∑∑⎪⎭⎫ ⎝⎛-=--⎪⎭⎫ ⎝⎛-=121)1(21)(1121112-∞=-=-=∑z z n n n ,21||<z (4)∑∞=-=11)(n n z n z X 由于∑∑∞=----∞=-=-=-=121111)()(1)(n n n n z z z z n n dz z dX ,1||>z 则zzz z z X -=--=1ln )1ln(ln )( 而)(z X 的收敛域和)()(z X z dX 的收敛域相同,所以)(z X 的收敛域为1||>z 。