概率分布与数学期望

32 30 17 21 0 1 2 3 1.27 100 100 100 100
这个数能否作为 X的平均值呢？
若统计100天,
可以想象, 若另外统计100天, 车工小张不出废品, 这另外100天每天的平均废品数也不一定是1.27. 一般来说, 若统计n天 ,
(假定小张每天至多出三件废品)
又设飞机机翼受到的正压力W 是V 的函数 : W kV 2 ( k 0, 常数), 求W 的数学期望.
解: 由上面的公式
1 1 2 E (W ) kv f (v )dv kv dv ka a 3 0
2 2

a
例7 设二维连续型随机变量（X , Y）的概率密度为
A sin( x y ) 0 x , 0 y f ( x, y) 2 2 0 其它 (1)求系数A , ( 2)求E ( X ), E ( XY ).
x f ( x )x
i i i
i
阴影面积近似为
这正是:


f ( xi )xi

x f ( x )dx
的渐近和式.
小区间[xi, xi+1)
定义: 设X是连续型随机变量, 其密度函数为 f (x), 如果积分: xf ( x )dx
概率论


绝对收敛, 则称此积分值为X的数学期望, 即:
2. 设二维连续型随机变量 (X, Y) 的联合概率密度为 f (x, y), 则： E ( X )
E (Y )


xf X ( x )dx

yfY
( y )dy




xf ( x , y )dxdy,

定性
质量控制：在生产 过程中，方差用于 衡量产品质量的一 致性和稳定性，通 过控制产品质量指 标的方差来提高产
品质量
社会科学研究： 在社会科学研究 中，方差用于分 析调查数据的变 异性和不确定性， 以及比较不同样
本之间的差异
期望与方差在金融领域的应用
风险评估：用于衡量投资组合的风 险和预期收益
资本资产定价模型（CAPM）：用 于确定资产的预期收益率，并评估 市场风险
定义：离散概率 分布的方差是各 个可能结果与期 望值的差的平方 的期望值。
计算公式：方差 = Σ (p(x) * (x μ)²)，其中p(x) 是概率，μ是期 望值。
举例：假设一个随 机变量X只取两个 值，X=0的概率为 0.5，X=1的概率 为0.5，则方差 = (0.5 * (0 - μ)² + 0.5 * (1 - μ)²)。
添加标题
添加标题
添加标题
添加标题
资产定价：为金融资产（如股票、 债券等）定价，以确定其内在价值
投资组合优化：通过期望和方差等 参数，选择最佳投资组合以最大化 预期收益并最小化风险
感谢您的观看
汇报人：XX
方差的定义
方差是衡量数据点与平均值之间离散程度的统计量。
方差计算公式为：方差 = Σ((数据点 - 平均值)^2) / 数据点个数。
方差的值越小，说明数据点越接近平均值，离散程度越小；方差的值越大，说明数据点离散程度越 大。
方差在概率分布中表示随机变量取值的不确定性程度。
离散概率分布的方差计算
注意事项：可能不是整数
连续概率分布的期望值计算
定义：连续概率分 布的期望值是所有 可能取值的加权平 均值，其中每个取 值的权重为其概率 密度函数在该点的

0 . 0779
E ( Y ) 2732 . 15 , 即平均一台收费
2732 . 15 .
13
例4 为普查某种疾病, n 个人需验血. 验血方 案有如下两种： (1) 分别化验每个人的血, 共需化验 n 次； (2) 分组化验, k 个人的血混在一起化验, 若 结果为阴性, 则只需化验一次; 若为阳性, 则 对 k 个人的血逐个化验, 找出有病者, 此时 k 个人的血需化验 k + 1 次. 设每人血液化验呈阳性的概率为 p, 且 每人化验结果是相互独立的.试说明选择哪 一方案较经济.
xf ( x)dx
绝对收敛, 则称此积分为 X 的数学期望
记作 E( X ), 即
E( X )

xf ( x)dx

数学期望的本质 —— 加权平均 它是一个数不再是随机变量
6
例1 甲、乙两选手进行打靶，击中环数 为X1,X2，它们的分布律为
X1 pk X2 pk 7 0.2 7 0.3 8 0.3 8 0.5 9 0.4 9 0.1 10 0.1 10 0.1
数学期望的概念源于此
4
数学期望的定义
设 X 为离散 随机变量. 其分布律为
P( X xk ) pk ,
k 1
k 1,2,
若无穷级数 xk pk 绝对收敛, 则称
其和为 X 的数学期望 记作 E( X ), 即
E ( X ) xk p k
k 1
5

定义
设连续型随机变量X 的密度为 f (x) 若广义积分
20
E 例9 设 X 服从参数为 的泊松分布，求 X 。
解：已知泊松分布律为：
PX k

§4.3 随机变量函数的数学期望 例题
§4.3 随机变量函数的数学期望 例题
§4.3 随机变量函数的数学期望 例题
概率论与数理统计
§4.4 协方差和相关系数
协方差 相关系数 授课内容 例题
§4.4 协方差和相关系数 协方差
1. 定义
§4.4 协方差和相关系数 协方差
2. 协方差的计算公式
概率论与数理统计
§4.1 数学期望
离散型随机变量的数学期望
连续型随机变量的数学期望
授课内容
数学期望的性质
§4.1 数学期望 离散型随机变量的数学期望
1. 定义
§4.1 数学期望 离散型随机变量的数学期望
关于定义的几点说明
(2) 级数的绝对收敛性保证了级数的和不随级数各项次序的改变 而改变 , 之所以这样要求是因为数学期望是反映随机变量X 取可能值 的平均值,它不应随可能值的排列次序而改变.
§4.4 协方差和相关系数 相关系数
3. 不相关的定义
§4.4 协方差和相关系数 相关系数
4. 不相关性的判定
以下四个条件等价 (1) ρ 0; (2)Cov( X ,Y ) 0; (3) D( X Y ) DX DY;
(4)3 随机变量函数的数学期望 二维随机变量函数的数学期望
§4.3 随机变量函数的数学期望 二维随机变量函数的数学期望
一维随机变量函数的数学期望 二维随机变量函数的数学期望 授课内容 例题
§4.3 随机变量函数的数学期望 例题
§4.3 随机变量函数的数学期望 例题
§4.3 随机变量函数的数学期望 例题
5 .不相关与相互独立的关系
协方差 相关系数 授课内容 例题
§4.4 协方差和相关系数 例题

概率分布与期望值计算详解一、概率分布概述概率分布是描述随机变量所有可能取值及其对应概率的数学工具。

根据随机变量的性质，概率分布可分为离散概率分布和连续概率分布。

离散概率分布描述的是离散型随机变量，即只能取有限个或可数个值的随机变量的概率分布情况；而连续概率分布则描述的是连续型随机变量，即可以在某个区间内取任意实数值的随机变量的概率分布情况。

二、常见的离散概率分布1. 0-1分布：一个随机试验只有两个可能结果，且这两个结果发生的概率之和为1。

例如，抛掷一枚硬币，正面朝上和反面朝上的概率分别为$p$和$1-p$。

2. 二项分布：在$n$次独立的伯努利试验中，成功次数$X$的概率分布。

例如，在10次抛掷硬币试验中，正好出现5次正面的概率。

3. 泊松分布：描述单位时间（或单位面积）内随机事件发生的次数的概率分布。

常用于描述稀有事件的概率分布情况。

三、常见的连续概率分布1. 正态分布：又称为高斯分布，是一种连续型概率分布。

正态分布具有钟形曲线特征，其均值、中位数和众数均为同一个值。

在自然界和社会科学中，许多随机现象都服从正态分布。

2. 指数分布：描述随机事件发生间隔时间的概率分布。

例如，电子产品的寿命、电话故障间隔时间等。

3. 均匀分布：在连续区间$[a, b]$内取值的随机变量的概率分布。

在这个区间内，随机变量取任何值的概率都相等。

四、期望值的计算期望值（Expected Value）是随机变量所有可能取值与其对应概率的乘积之和，用数学符号表示即为$E(X) = \sum_{i=1}^{n} x_i p(x_i)$。

期望值反映了随机变量的长期平均结果或平均水平。

计算期望值的一般步骤如下：1. 确定随机变量的所有可能取值$x_1, x_2, ..., x_n$。

2. 确定每个取值对应的概率$p(x_1), p(x_2), ..., p(x_n)$。

3. 将每个取值与其对应的概率相乘，得到$x_1 p(x_1), x_2 p(x_2), ..., x_n p(x_n)$。

概率的分布与期望概率是一种描述事件发生可能性的数学工具，而概率的分布与期望则是概率论中重要的概念之一。

本文将介绍概率分布和期望的概念及其与实际问题的应用。

一、概率分布概率分布是描述一个随机变量所有可能取值及其对应概率的函数。

常见的概率分布包括离散概率分布和连续概率分布。

1.离散概率分布离散概率分布用于描述随机变量取有限或可数多个值的概率情况。

其中最常见的是二项分布和泊松分布。

二项分布是一种重要的离散概率分布，用于描述n次独立重复试验中成功次数的概率分布。

在二项分布中，每次试验有两种可能的结果，成功或失败，成功的概率为p，失败的概率为1-p。

其概率质量函数为P(X=k)=C(n,k)*p^k*(1-p)^(n-k)，其中X为成功次数，k为取值范围内的一个值，C(n,k)表示组合数。

泊松分布用于描述在一定时间或空间内，事件发生的次数的概率分布。

泊松分布的概率质量函数为P(X=k)=(λ^k * e^-λ)/k!，其中X为事件发生次数，k为取值范围内的一个值，λ为事件发生的平均次数。

2.连续概率分布连续概率分布用于描述随机变量在一定区间内取值的概率情况。

其中最常见的是均匀分布、正态分布和指数分布。

均匀分布是一种简单的连续概率分布，它的概率密度函数在取值范围内是常数。

均匀分布的概率密度函数为f(x)=1/(b-a)，其中a为最小值，b为最大值。

正态分布（高斯分布）是一种常见的连续概率分布，广泛应用于自然和社会科学领域。

正态分布的概率密度函数为f(x)=(1/√(2πσ^2))*e^((x-μ)^2/(2σ^2))，其中μ为均值，σ为标准差。

指数分布用于描述事件发生的时间间隔的概率分布，如等待时间、生命周期等。

指数分布的概率密度函数为f(x)=λ*e^(-λx)，其中λ为每单位时间发生事件的平均次数。

二、期望期望是一个概率分布的数学期望，用于描述随机变量的平均值。

期望可以看作是随机变量在大量重复实验中出现的平均值。

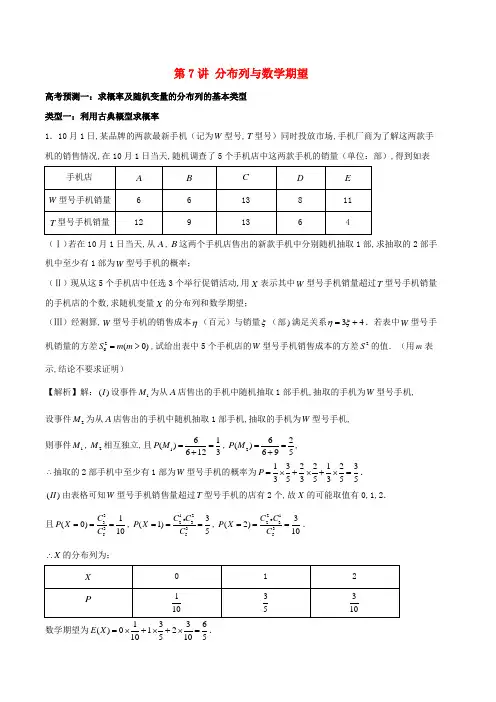
第7讲 分布列与数学期望高考预测一：求概率及随机变量的分布列的基本类型 类型一：利用古典概型求概率1．10月1日,某品牌的两款最新手机（记为W 型号,T 型号）同时投放市场,手机厂商为了解这两款手机的销售情况,在10月1日当天,随机调查了5个手机店中这两款手机的销量（单位：部）,得到如表（Ⅰ）若在10月1日当天,从A ,B 这两个手机店售出的新款手机中分别随机抽取1部,求抽取的2部手机中至少有1部为W 型号手机的概率；（Ⅱ）现从这5个手机店中任选3个举行促销活动,用X 表示其中W 型号手机销量超过T 型号手机销量的手机店的个数,求随机变量X 的分布列和数学期望；（Ⅲ）经测算,W 型号手机的销售成本η（百元）与销量ξ（部)满足关系34ηξ=+．若表中W 型号手机销量的方差20(0)S m m =>,试给出表中5个手机店的W 型号手机销售成本的方差2S 的值．（用m 表示,结论不要求证明）【解析】解：()I 设事件1M 为从A 店售出的手机中随机抽取1部手机,抽取的手机为W 型号手机, 设事件2M 为从A 店售出的手机中随机抽取1部手机,抽取的手机为W 型号手机, 则事件1M ,2M 相互独立,且161()6123P M ==+,262()695P M ==+, ∴抽取的2部手机中至少有1部为W 型号手机的概率为13221233535355P =⨯+⨯+⨯=．()II 由表格可知W 型号手机销售量超过T 型号手机的店有2个,故X 的可能取值有0,1,2．且33351(0)10C P X C ===,1223353(1)5C C P X C ===,2123353(2)10C C P X C ===． X ∴的分布列为：数学期望为1336()012105105E X =⨯+⨯+⨯=．20()()III D s m ξ==,34ηξ=+,2()9()9S D D m ηξ∴===．2．为了研究一种新药的疗效,选100名患者随机分成两组,每组各50名,一组服药,另一组不服药．一段时间后,记录了两组患者的生理指标x 和y 的数据,并制成如图,其中“*”表示服药者,“+”表示未服药者．（1）从服药的50名患者中随机选出一人,求此人指标y 的值小于60的概率；（2）从图中A ,B ,C ,D 四人中随机选出两人,记ξ为选出的两人中指标x 的值大于1.7的人数,求ξ的分布列和数学期望()E ξ；（3）试判断这100名患者中服药者指标y 数据的方差与未服药者指标y 数据的方差的大小．（只需写出结论）【解析】解：（1）由图知：在50名服药患者中,有15名患者指标y 的值小于60, 答：从服药的50名患者中随机选出一人,此人指标小于60的概率为：1535010p ==． （2）由图知：A 、C 两人指标x 的值大于1.7,而B 、D 两人则小于1.7,可知在四人中随机选项出的2人中指标x 的值大于1.7的人数ξ的可能取值为0,1,2, 2411(0)6P C ξ===, 1122242(1)3C C P C ξ===,2411(2)6P C ξ===, ξ∴的分布列如下：答：121()0121636E ξ=⨯+⨯+⨯=．（3）答：由图知100名患者中服药者指标y 数据的方差比未服药者指标y 数据的方差大．3．已知2件次品和3件正品混放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束． （1）求第一次检测出的是次品且第二次检测出的是正品的概率；（2）已知每检测一件产品需要费用100元,设X 表示直到检测出2件次品或者检测出3件正品时所需要的检测费用（单位：元）,求X 的分布列和数学期望．【解析】解：（1）记“第一次检测出的是次品且第二次检测出的是正品”为事件A ,则P （A ）1123252332010A A A ⨯===； （2）X 的可能取值为200,300,400,222521(200)2010A P X A ====,311232323562323(300)6010A C C A P X A ++⨯⨯====, 133(400)1(200)(300)110105P X P X P X ==-=-==--=； 所以X的分布列为：数学期望为13320030040035010105EX =⨯+⨯+⨯=． 类型二：利用相互独立事件的概率乘法公式和互斥事件概率加法公式求概率 4．电影公司随机收集了电影的有关数据,经分类整理得到下表：好评率是指：一类电影中获得好评的部数与该类电影的部数的比值． 假设所有电影是否获得好评相互独立．（Ⅰ）从电影公司收集的电影中随机选取1部,求这部电影是获得好评的第四类电影的概率； （Ⅱ）从第四类电影和第五类电影中各随机选取1部,估计恰有1部获得好评的概率；（Ⅲ）假设每类电影得到人们喜欢的概率与表格中该类电影的好评率相等．用“1k ξ=”表示第k 类电影得到人们喜欢．“0k ξ=”表示第k 类电影没有得到人们喜欢(1k =,2,3,4,5,6)．写出方差1D ξ,2D ξ,3D ξ,4D ξ,5D ξ,6D ξ的大小关系．【解析】解：（Ⅰ）设事件A 表示“从电影公司收集的电影中随机选取1部,求这部电影是获得好评的第四类电影”,总的电影部数为140503002008005102000+++++=部, 第四类电影中获得好评的电影有：2000.2550⨯=部,∴从电影公司收集的电影中随机选取1部,求这部电影是获得好评的第四类电影的频率为：P （A ）500.0252000==． （Ⅱ）设事件B 表示“从第四类电影和第五类电影中各随机选取1部,恰有1部获得好评”, 第四类获得好评的有：2000.2550⨯=部, 第五类获得好评的有：8000.2160⨯=部,则从第四类电影和第五类电影中各随机选取1部,估计恰有1部获得好评的概率：P （B ）50(800160)(20050)1600.35200800⨯-+-⨯==⨯．（Ⅲ）由题意知,定义随机变量如下：0,1,k k k ξ⎧=⎨⎩第类电影没有得到人们喜欢第类电影得到人们喜欢,则k ξ服从两点分布,则六类电影的分布列及方差计算如下： 第一类电影：1()10.400.60.4E ξ=⨯+⨯=,221()(10.4)0.4(00.4)0.60.24D ξ=-⨯+-⨯=．第二类电影：2()10.200.80.2E ξ=⨯+⨯=,222()(10.2)0.2(00.2)0.80.16D ξ=-⨯+-⨯=．第三类电影：3()10.1500.850.15E ξ=⨯+⨯=,223()(10.15)0.15(00.15)0.850.1275D ξ=-⨯+-⨯=．第四类电影：4()10.2500.750.25E ξ=⨯+⨯=,224()(10.25)0.25(00.25)0.750.1875D ξ=-⨯+-⨯=．第五类电影：5()10.200.80.2E ξ=⨯+⨯=,225()(10.2)0.2(00.2)0.80.16D ξ=-⨯+-⨯=．第六类电影：6()10.100.90.1E ξ=⨯+⨯=,225()(10.1)0.1(00.1)0.90.09D ξ=-⨯+-⨯=．∴方差1D ξ,2D ξ,3D ξ,4D ξ,5D ξ,6D ξ的大小关系为：632541D D D D D D ξξξξξξ<<=<<．5．设甲、乙两位同学上学期间,每天7:30之前到校的概率均为23．假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立．（1）设甲同学上学期间的三天中7:30之前到校的天数为X ,求0X =,1X =,2X =,3X =时的概率(0)P X =,(1)P X =,(2)P X =,(3)P X =．（2）设M 为事件“上学期间的三天中,甲同学在7:30之前到校的天数比乙同学在7:30之前到校的天数恰好多2”,求事件M 发生的概率．【解析】解：（1）321(0)(1)327P X ==-=,123222(1)(1)339P X C ==-=, 223224(2)()(1)339P X C ==-=,33328(3)()327P X C ===． （2）设乙同学上学期间的三天中在7:30之前到校的天数为Y , 则1(0)(0)27P Y P X ====,2(1)(1)9P Y P X ====, 4(2)(2)9P Y P X ====,8(3)(3)27P Y P X ====, 418220()(2)(0)(3)(1)927279243P M P X P Y P X P Y ∴===+===⨯+⨯=． 类型三：利用条件概率公式求概率6．如图所示,质点P 在正方形ABCD 的四个顶点上按逆时针方向前进．现在投掷一个质地均匀、每个面上标有一个数字的正方体玩具,它的六个面上分别写有两个1、两个2、两个3一共六个数字．质点P 从A 点出发,规则如下：当正方体上底面出现的数字是1,质点P 前进一步（如由A 到)B ；当正方体上底面出现的数字是2,质点P 前两步（如由A 到)C ,当正方体上底面出现的数字是3,质点P 前进三步（如由A 到)D ．在质点P 转一圈之前连续投掷,若超过一圈,则投掷终止．（1）求点P 恰好返回到A 点的概率；（2）在点P 转一圈恰能返回到A 点的所有结果中,用随机变量ξ表示点P 恰能返回到A 点的投掷次数,求ξ的分布列及数学期望．【解析】解：（1）投掷一次正方体玩具,因每个数字在上底面出现是等可能的,故其概率12163P ==． 易知只投掷一次不可能返回到A 点．①若投掷两次质点P 就恰好能返回到A 点,则上底面出现的两个数字,应依次为：(1,3)、(3,1)、(2,2)三种结果,其概率为2211()333P =⨯=．②若投掷三次质点P 恰能返回到A 点,则上底面出现的三个数字,应依次为：(1,1,2)、(1,2,1)、(2,1,1)三种结果,其概率为3311()339P =⨯=． ③若投掷四次质点P 恰能返回到A 点,则上底面出现的四个数字应依次为：(1,1,1,1),其概率为4411()381P ==．所以,质点P 恰好返回到A 点的概率为：23411137398181P P P P =++=++=．（2）由（1）知,质点P 转一圈恰能返回到A 点的所有结果共有以上问题中的7种情况, 且ξ的可能取值为2,3,4．则1273(2)373781P ξ===,199(3)373781P ξ===,1181(4)373781P ξ===,故ξ的分布列为：所以,27918523437373737E ξ=⨯+⨯+⨯=．7．根据以往的经验,某工程施工期间的降水量X （单位：)mm 对工期的影响如下表：300700X <700900X <9002610历年气象资料表明,该工程施工期间降水量X 小于300,700,900的概率分别为0.3,0.7,0.9,求： ()I 工期延误天数Y 的均值与方差；（Ⅱ）在降水量X 至少是300的条件下,工期延误不超过6天的概率．【解析】()I 由题意,(300)0.3P X <=,(300700)(700)(300)0.70.30.4P X P X P X <=<-<=-=,(700900)(900)(700)0.90.70.2P X P X P X <=<-<=-=,(900)10.90.1P X =-=Y 的分布列为()00.320.460.2100.13E Y ∴=⨯+⨯+⨯+⨯=2222()(03)0.3(23)0.4(63)0.2(103)0.19.8D Y =-⨯+-⨯+-⨯+-⨯=∴工期延误天数Y 的均值为3,方差为9.8；（Ⅱ）(300)1(300)0.7P X P X =-<=,(300900)(900)(300)0.90.30.6P X P X P X <=<-<=-= 由条件概率可得(300900)0.66(6|300)(300)0.77P X P Y X P X <===．类型四：利用统计图表中的数据求概率8．某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完．根据往年销售经验,每天需求量与当天最高气温（单位：C)︒有关．如果最高气温不低于25,需求量为500瓶；如果最高气温位于区间[20,25),需求量为300瓶；如果最高气温低于20,需求量为200瓶．为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表：以最高气温位于各区间的频率代替最高气温位于该区间的概率． （1）求六月份这种酸奶一天的需求量X （单位：瓶）的分布列；（2）设六月份一天销售这种酸奶的利润为Y （单位：元）,当六月份这种酸奶一天的进货量n （单位：瓶）为多少时,Y 的数学期望达到最大值？【解析】解：（1）由题意知X 的可能取值为200,300,500,216(200)0.290P X +===,36(300)0.490P X ===, 2574(500)0.490P X ++===, X ∴的分布列为：（2）由题意知这种酸奶一天的需求量至多为500瓶,至少为200瓶,∴只需考虑200500n ,当300500n 时,若最高气温不低于25,则642Y n n n =-=；若最高气温位于区间[20,25),则63002(300)412002Y n n n =⨯+--=-； 若最高气温低于20,则62002(200)48002Y n n n =⨯+--=-, 20.4(12002)0.4(8002)0.26400.4EY n n n n ∴=⨯+-⨯+-⨯=-,当200300n 时,若最高气温不低于20,则642Y n n n =-=,若最高气温低于20,则62002(200)48002Y n n n =⨯+--=-, 2(0.40.4)(8002)0.2160 1.2EY n n n ∴=⨯++-⨯=+．300n ∴=时,Y 的数学期望达到最大值,最大值为520元．9．某贫困地区共有1500户居民,其中平原地区1050户,山区450户．为调查该地区2017年家庭收入情况,从而更好地实施“精准扶贫”,采用分层抽样的方法,收集了150户家庭2017年年收入的样本数据（单位：万元）．（1）应收集多少户山区家庭的样本数据？（2）根据这150个样本数据,得到2017年家庭收入的频率分布直方图（如图所示）,其中样本数据分组区间为(0,0.5],(0.5,1],(1,1.5],(1.5,2],(2,2.5],(2.5,3]．如果将频率视为概率,估计该地区2017年家庭收入超过1.5万元的概率；（3）样本数据中,有5户山区家庭的年收入超过2万元,请完成2017年家庭收入与地区的列联表,并判断是否有90%的把握认为“该地区2017年家庭年收入与地区有关”？附：2() n ad bcK-=++++2)k【解析】解：（1）由已知可得每户居民被抽取的概率为0.1,故应收集手机4500.145⨯=户山区家庭的样本数据．（2）由直方图可知该地区2017年家庭年收入超过1.5万元的概率约为(0.5000.3000.100)0.50.45++⨯=．（3）样本数据中,年收入超过2万元的户数为(0.3000.100)0.515030+⨯⨯=户．而样本数据中,有5户山区家庭的年收入超过2万元,故列联表如下：所以2150(2540580)2003.175 2.706 301201054563K⨯-⨯==≈>⨯⨯⨯,∴有90%的把握认为“该地区2017年家庭年收入与地区有关”．高考预测二：超几何分布和二项分布类型一：超几何分布10．已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16．现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查．（Ⅰ）应从甲、乙、丙三个部门的员工中分别抽取多少人？（Ⅱ）若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查． ()i 用X 表示抽取的3人中睡眠不足的员工人数,求随机变量X 的分布列与数学期望；()ii 设A 为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A 发生的概率．【解析】解：（Ⅰ）单位甲、乙、丙三个部门的员工人数分别为24,16,16．人数比为：3:2:2, 从中抽取7人现,应从甲、乙、丙三个部门的员工中分别抽取3,2,2人．（Ⅱ）若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查． ()i 用X 表示抽取的3人中睡眠不足的员工人数,随机变量X 的取值为：0,1,2,3,34337()k kC C P X k C -⋅==,0k =,1,2,3． 所以随机变量的分布列为：随机变量X 的数学期望11218412()0123353535357E X =⨯+⨯+⨯+⨯=； ()ii 设A 为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,设事件B 为：抽取的3人中,睡眠充足的员工有1人,睡眠不足的员工有2人,事件C 为抽取的3人中, 睡眠充足的员工有2人,睡眠不足的员工有1人, 则：A BC =,且P （B ）(2)P X ==,P （C ）(1)P X ==,故P （A ）6()(2)(1)7P B C P X P X ===+==． 所以事件A 发生的概率：67． 11． 2.5PM 是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物． 2.5PM 日均值在35微克/立方米以下空气质量为一级；在35微克/立方米~75微克/立方米之间空气质量为二级；在75微克/立方米以上空气质量为超标．石景山古城地区2013年2月6日至15日每天的 2.5PM 监测数据如茎叶图所示．（1）小陈在此期间的某天曾经来此地旅游,求当天 2.5PM 日均监测数据未超标的概率；（2）从所给10天的数据中任意抽取三天数据,记ξ表示抽到 2.5PM 监测数据超标的天数,求ξ的分布列及期望．【解析】解：（1）记“当天 2.5PM 日均监测数据未超标”为事件A , 因为有24+天 2.5PM 日均值在75微克/立方米以下, 故P （A ）243105+==． （2）ξ的可能值为0,1,2,3．由茎叶图可知：空气质量为一级的有2天,空气质量为二级的有4天,只有这6天空气质量不超标,而其余4天都超标．363101(0)6C P C ξ===,21643101(1)2C C P C ξ===,12643103(2)10C C P C ξ===,343101(3)30C P C ξ===．ξ的分布列如下表：1131601236210305E ξ∴=⨯+⨯+⨯+⨯=．类型二：二项分布12．某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖,每次抽奖都是从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出一个球,在摸出的2个球中,若都是红球,则获得一等奖；若只有1个红球,则获得二等奖；若没有红球,则不获奖． （1）求顾客抽奖1次能获奖的概率；（2）若某顾客有3次抽奖机会,记该顾客在3次抽奖中或一等奖的次数为X ,求X 的分布列、数学期望和方差．【解析】解：（1）设顾客抽奖1次能中奖的概率为P ．116511101037111010C C P C C =-=-=,（2）设该顾客在一次抽奖中获一等奖的概率为1P ,1145112101015C C P C C ==, 故而1?(3,)5X B ．3464(0)()5125P X ∴===,1231448(1)()55125P X C ===, 2231412(2)()55125P X C ===,311(3)()5125P X ===． 故X 的分布列为数学期望13()355E X ==,方差1412()35525D X ==． 13．近年来,空气质量成为人们越来越关注的话题,空气质量指数(,)AirQualityIndex AQI 是定量描述空气质量状况的指数,空气质量按照AQI 大小分为六级,0~50为优；51~100为良；101~150为轻度污染；151~200为中度污染；201~300为重度污染；大于300为严重污染．环保部门记录了2017年某月哈尔滨市10天的AQI 的茎叶图如下：（1）利用该样本估计该地本月空气质量优良(100)AQI 的天数；（按这个月总共30天计算） （2）现工作人员从这10天中空气质量为优良的日子里随机抽取2天进行某项研究,求抽取的2天中至少有一天空气质量是优的概率；（3）将频率视为概率,从本月中随机抽取3天,记空气质量优良的天数为ξ,求ξ的概率分布列和数学期望．【解析】解：（1）从茎叶图中可发现该样本中空气质量优的天数为2,空气质量良的天数为4,故该样本中空气质量优良的频率为63105=,从而估计该月空气质量优良的天数为330185⨯=（2）现工作人员从这10天中空气质量为优良的日子里随机抽取2天进行某项研究, 基本事件总数2615n C ==,抽取的2天中至少有一天空气质量是优的对立事件是抽取的2天中至少有一天空气质量都不是优,∴抽取的2天中至少有一天空气质量是优的概率：2426315C p C =-=．（3）由（1）估计某天空气质量优良的概率为35,ξ∴的所有可能取值为0,1,2,3,且3~(3,)5B ξ,328(0)()5125P ξ===, 1233236(1)()55125P C ξ===, 2233254(2)()55125P C ξ===, 3327(3)()5125P ξ===, 故ξ的分布列为：3~(3,)5B ξ,33 1.85E ξ=⨯=．高考预测三：概率与其他知识点交汇 类型一：以其他知识为载体14．已知正四棱锥PABCD 的侧棱和底面边长相等,在这个正四棱锥的8条棱中任取两条,按下列方式定义随机变量ξ的值：若这两条棱所在的直线相交,则ξ的值是这两条棱所在直线的夹角大小（弧度制）； 若这两条棱所在的直线平行,则0ξ=；若这两条棱所在的直线异面,则ξ的值是这两条棱所在直线所成角的大小（弧度制）． （1）求(0)P ξ=的值；（2）求随机变量ξ的分布列及数学期望()E ξ．【解析】解：（1）根据题意,该四棱锥的四个侧面均为等边三角形,底面为正方形,PAC ∆,PBD ∆为等腰直角三角形．ξ的可能取值为：0,3π,2π, 在这个正四棱锥的8条棱中任取两条基本事件总数2828n C ==种情况, 当0ξ=时有2种,当3πξ=时有342420⨯+⨯=种,当2πξ=时有246+=种．21(0)2814P ξ∴===． （2）21(0)2814P ξ===． 205()3287P πξ===, 63()22814P πξ===．随机变量ξ的分布列如下表：15329()0143721484E πππξ=⨯+⨯+⨯=． 15．从集合{1M =,2,3,4,5,6,7,8,9}中抽取三个不同的元素构成子集1{a ,2a ,3}a ． （1）求对任意的i 和(1j i =,2,3,1j =,2,3,)i j ≠满足||2i j a a -的概率；（2）若1a ,2a ,3a 成等差数列,设其公差为(0)ξξ>,求随机变量ξ的分布列与数学期望()E ξ．【解析】解：（1）由题意知基本事件数为3984C =,而满足条件||2i j a a -,即取出的元素不相邻,则用插空法有3735C =种,故所求事件的概率为3558412P ==； （2）分析1a ,2a ,3a 成等差数列的情况：1ξ=的情况有7种：{1,2,3},{2,3,4},{3,4,5},{4,5,6},{5,6,7},{6,7,8},{7,8,9}, 2ξ=的情况有5种：{1,3,5},{2,4,6},{3,5,7},{4,6,8},{5,7,9}． 3ξ=的情况有3种：{1,4,7},{2,5,8},{3,6,9}．4ξ=的情况有1种：{1,5,9}．故ξ的分布列如下：所以753115()1234161615168E ξ=⨯+⨯+⨯+⨯=． 类型二：构造递推关系求概率问题16．为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验．试验方案如下：每一轮选取两只白鼠对药效进行对比试验．对于两只白鼠,随机选一只施以甲药,另一只施以乙药．一轮的治疗结果得出后,再安排下一轮试验．当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效．为了方便描述问题,约定：对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得1-分；若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得1-分；若都治愈或都未治愈则两种药均得0分．甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X ． （1）求X 的分布列；（2）若甲药、乙药在试验开始时都赋予4分,(0i p i =,1,⋯,8)表示“甲药的累计得分为i 时,最终认为甲药比乙药更有效”的概率,则00p =,81p =,11(1i i i i p ap bp cp i -+=++=,2,⋯,7),其中(1)a P X ==-,(0)b P X ==,(1)c P X ==．假设0.5α=,0.8β=． ()i 证明：1{}(0i i p p i +-=,1,2,⋯,7)为等比数列； ()ii 求4p ,并根据4p 的值解释这种试验方案的合理性．【解析】（1）解：X 的所有可能取值为1-,0,1．(1)(1)P X αβ=-=-,(0)(1)(1)P X αβαβ==+--,(1)(1)P X αβ==-,X ∴的分布列为：（2）()i 证明：0.5α=,0.8β=,∴由（1）得,0.4a =,0.5b =,0.1c =．因此110.40.50.1(1i i i i p p p p i -+=++=,2,⋯,7),故110.1()0.4()i i i i p p p p +--=-,即11()4()i i i i p p p p +--=-,又1010p p p -=≠,1{}(0i i p p i +∴-=,1,2,⋯,7)为公比为4,首项为1p 的等比数列；()ii 解：由()i 可得,881887761001(14)41()()()143p p p p p p p p p p --=-+-+⋯+-+==-,81p =,18341p ∴=-, 444332*********()()()()3257p p p p p p p p p p p -∴=-+-+-+-+==． 4p 表示最终认为甲药更有效的概率．由计算结果可以看出,在甲药治愈率为0.5,乙药治愈率为0.8时,认为甲药更有效的概率为410.0039257p =≈,此时得出错误结论的概率非常小,说明这种试验方案合理． 17．从原点出发的某质点M ,按向量(0,1)a =移动的概率为23,按向量(0,2)b =移动的概率为13,设M 可到达点(0,)(1n n =,2,3,)⋯的概率为n P ． （1）求1P 和2P 的值；（2）求证：2111()3n n n n P P P P +++-=--；（3）求n P 的表达式．【解析】解：（1）123P =,22217()339P =+= （2）证明：M 点到达点(0,2)n +有两种情况 ①从点(0,1)n +按向量(0,1)a =移动 ②从点(0,)n 按向量(0,2)b =移动∴212133n n n P P P ++=+ ∴2111()3n n n n P P P P +++-=-- 问题得证．（3）数列1{}n n P P +-是以21P P -为首项,13-为公比的等比数列 1111211111()()()()3933n n n n n P P P P --++-=--=-=- 11()3n n n P P -∴-=-又因为111221()()()n n n n n P P P P P P P P ----=-+-+⋯+-12111()()()333n n -=-+-+⋯+-111[1()]123n -=-- 11n n P P P P ∴=-+∴113()434n n P =⨯-+． 类型三：利用导数研究概率问题18．某工厂的某种产品成箱包装,每箱200件,每一箱产品在交付用户之前要对产品作检验,如检验出不合格品,则更换为合格品．检验时,先从这箱产品中任取20件作检验,再根据检验结果决定是否对余下的所有产品作检验,设每件产品为不合格品的概率都为(01)p p <<,且各件产品是否为不合格品相互独立．（1）记20件产品中恰有2件不合格品的概率为()f p ,求()()f p f p 的最大值点0p （即()f p 取最大值时对应的p 的值）．（2）现对一箱产品检验了20件,结果恰有2件不合格品,以（1）中确定的0p 作为p 的值,已知每件产品的检验费用为3元,若有不合格品进入用户手中,则工厂要对每件不合格品支付28元的赔偿费用 ()i 若不对该箱余下的产品作检验,这一箱产品的检验费用与赔偿费用之和记为X 求()E X ； ()ii 以检验费用与赔偿费用和的期望值为决策依据,是否该对这箱余下的所有产品作检验？【解析】解：（1）记20件产品中恰有2件不合格品的概率为()f p ,则221820()(1)f p C p p =-,2182172172020()[2(1)18(1)]2(1)(110)f p C p p p p C p p p ∴'=---=--,令()0f p '=,得0.1p =, 当(0,0.1)p ∈时,()0f p '>, 当(0.1,1)p ∈时,()0f p '<, f ∴()p 的最大值点00.1p =．（2）()i 由（1）知0.1p =,令Y 表示余下的180件产品中的不合格品数,依题意知~(180,0.1)Y B ,20328X Y =⨯+,即6028X Y =+,()(6028)6028()60281800.1564E X E Y E Y ∴=+=+=+⨯⨯=． ()ii 如果对余下的产品作检验,由这一箱产品所需要的检验费为600元, ()564600E X =<,∴应该对余下的产品不进行检验．19．某有机水果种植基地试验种植的某水果在售卖前要成箱包装,每箱80个,每一箱水果在交付顾客之前要按约定标准对水果作检测,如检测出不合格品,则更换为合格品．检测时,先从这一箱水果中任取10个作检测,再根据检测结果决定是否对余下的所有水果作检测．设每个水果为不合格品的概率都为(01)p p <<,且各个水果是否为不合格品相互独立．（Ⅰ）记10个水果中恰有2个不合格品的概率为()f p ,求()f p 取最大值时p 的值0p ；（Ⅱ）现对一箱水果检验了10个,结果恰有2个不合格,以（Ⅰ）中确定的0p 作为p 的值．已知每个水果的检测费用为1.5元,若有不合格水果进入顾客手中,则种植基地要对每个不合格水果支付a 元的赔偿费用(*)a N ∈．（ⅰ）若不对该箱余下的水果作检验,这一箱水果的检验费用与赔偿费用的和记为X ,求EX ； （ⅱ）以检验费用与赔偿费用和的期望值为决策依据,当种植基地要对每个不合格水果支付的赔偿费用至少为多少元时,将促使种植基地对这箱余下的所有水果作检验？【解析】解：（Ⅰ）记10个水果中恰有2个不合格的概率为()f p ,则22810()(1)f p C p p =-,282710()[2(1)8(1)]f p C p p p p ∴'=---,由()0f p '=,得0.2p =．且当(0,0.2)p ∈时()0f p '>,当(0.2,1)p ∈时,()0f p '<,()f p ∴的最大值点00.2p =．（Ⅱ）由（Ⅰ）知00.2p =．（ⅰ）令Y 表示余下的70个水果中的不合格数,依题意~(70,0.2)Y B ,10 1.515X aY aY =⨯+=+． ()(15)15()15700.21514E X E aY aE Y a a ∴=+=+=+⨯⨯=+．（ⅱ）如果对余下的水果作检验,则这箱水果的检验费为120元, 由1514120a +>,得1057.514a >=,且*a N ∈, ∴当种植基地要对每个不合格水果支付的赔偿费用至少为8元时,将促使种植基地对这箱余下的所有水果作检验．高考预测三：决策问题20．某公司计划购买2台机器,该种机器使用三年后即被淘汰,机器有一易损零件,在购买机器时,可以额外购买这种零件作为备件,每个300元．在机器使用期间,如果备件不足再购买,则每个500元．现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得到下面柱状图．以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记X 表示2台机器三年内共需更换的易损零件数,n 表示购买2台机器的同时购买的易损零件数．（1）求X 的分布列；（2）若要求()0.5P X n ,试确定n 的最小值；（3）以购买易损零件所需费用的期望值为决策依据,在19n =与20n =之中选其一,应选用哪个？【解析】解：（1）每台机器更换的易损零件数为8,9,10,11,记事件1A 为第一台机器3年内换掉7i +个零件(1i =,2,3,4),记事件1B 为第二台机器3年内换掉7i +个零件(1i =,2,3,4),由题知134134()()()()()()0.2P A P A P A P B P B P B ======,22()()0.4P A P B ==,则X 的可能的取值为16,17,18,19,20,21,22,11(16)()()0.20.20.04P X P A P B ===⨯=；1221(17)()()()()0.20.40.40.20.16P X P A P B P A P B ==+=⨯+⨯=；132231(18)()()()()()()0.20.20.20.20.40.40.24P X P A P B P A P B P A P B ==++=⨯+⨯+⨯=；14233241(19)()()()()()()()()0.20.20.20.20.40.20.20.40.24P X P A P B P A P B P A P B P A P B ==+++=⨯+⨯+⨯+⨯=；243342(20)()()()()()()0.40.20.20.40.20.20.2P X P A P B P A P B P A P B ==++=⨯+⨯+⨯=；3443(21)()()()()0.20.20.20.20.08P X P A P B P A P B ==+=⨯+⨯=；44(22)()()0.20.20.04P X P A P B ===⨯=．从而X 的分布列为（2）要()0.5P x n ,0.040.160.240.5++<,0.040.160.240.240.5+++,则n 的最小值为19；（3）购买零件所需费用含两部分,一部分为购买机器时购买零件的费用,另一部分为备件不足时额外购买的费用,当19n =时,费用的期望为193005000.210000.0815000.045940⨯+⨯+⨯+⨯=元,当20n =时,费用的期望为203005000.0810000.046080⨯+⨯+⨯=元,若要费用最少,所以应选用19n =．高考预测四：正态分布21．为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸（单位：)cm ．根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布2(,)N μσ．（1）假设生产状态正常,记X 表示一天内抽取的16个零件中其尺寸在(3,3)μσμσ-+之外的零件数,求(1)P X ；（2）一天内抽检零件中,如果出现了尺寸在(3,3)μσμσ-+之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查．下面是检验员在一天内抽取的16个零件的尺寸：9.95 10.12 9.96 9.96 10.01 9.92 9.98 10.0410.26 9.91 10.13 10.02 9.22 10.04 10.05 9.95 经计算得16119.9716i i x x ===∑,0.212s =≈,其中i x 为抽取的第i 个零件的尺寸,1i =,2,⋯,16． 用样本平均数x 作为μ的估计值ˆμ,用样本标准差s 作为σ的估计值ˆσ,利用估计值判断是否需对当天的生产过程进行检查？剔除ˆˆˆˆ(3,3)μσμσ-+之外的数据,用剩下的数据估计μ和σ（精确到0.01)． 附：若随机变量Z 服从正态分布2(,)N μσ,则(33)0.9974P Z μσμσ-<<+=,160.99740.9592≈,0.09．【解析】解：（1）抽取的一个零件的尺寸在(3,3)μσμσ-+之内的概率为0.9974,从而零件的尺寸在(3,3)μσμσ-+之外的概率为0.0026,故~(16,0.0026)X B ．因此,16(1)1(0)10.99740.0408P X P X =-==-≈；（2）由9.97,0.212x s =≈,得μ的估计值为ˆ9.97μ=,σ的估计值为ˆ0.212σ=, 由样本数据可以看出有一个零件的尺寸在ˆˆˆˆ(3,3)μσμσ-+之外, 因此需对当天的生产过程进行检查,剔除ˆˆˆˆ(3,3)μσμσ-+之外的数据9.22, 剩下数据的平均数为1(169.979.22)10.0215⨯-=, 因此μ的估计值为10.02,162221160.212169.971591.134i i x ==⨯+⨯≈∑,剔除ˆˆˆˆ(3,3)μσμσ-+之外的数据9.22, 剩下数据的样本方差为221(1591.1349.221510.02)0.00815--⨯≈． 因此σ0.09．22．从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如图频率分布直方图：（1）求这500件产品质量指标值的样本平均值x 和样本方差2s （同一组的数据用该组区间的中点值作代表）；（2）由直方图可以认为,这种产品的质量指标Z 服从正态分布2(,)N μσ,其中μ近似为样本平均数x ,2σ近似为样本方差2s①利用该正态分布,求(187.8212.2)P Z <<②某用户从该企业购买了100件这种产品,记X 表示这100件产品中质量指标值位于区间(187.8,212.2)的产品件数．利用 ①的结果,求EX 附：6 2.44≈,若2~(,)z n μσ,则()0.6826p Z μσμσ-<<+=,(22)0.9544p Z μσμσ-<<+=．【解析】解：（1）抽取产品的质量指标值的样本平均数为：1700.021800.091900.222000.332100.242200.082300.02200x =⨯+⨯+⨯+⨯+⨯+⨯+⨯=,样本方差2s 分别为：2222222(30)0.02(20)0.09(10)0.2200.33100.24200.08300.02150s =-⨯+-⨯+-⨯+⨯+⨯+⨯+⨯=． （Ⅱ）()i 由（Ⅰ）知~(200,150)Z N ,从而(187.8212.2)(20012.220012.2)0.6826P Z P Z <<=-<<+=；()ii 由()i 知一件产品的质量指标值位于区间(187.8,212.2)的概率为0.6826,依题意知~(100,0.6826)X B ,所以1000.682668.26EX =⨯=．。

例谈离数型随机变量概率分布与数学期望数学期望=每个个数X 每个它的概率，再相加从2008年全国各省市高考数学试题中，概率统计考题，可谓“军书十二卷，卷卷有爷名”，显然它是高考的必考内容，特别是离散型随机变量概率分布与数学期望内容的考题分布极为广泛，确实是一个重要考点，但纵观其解法，可以归纳为定义法、公式法、分析法与变量推理法四种，2009年考生务必对上述四种解题方法引起高度重视，本文就其命题特点，解题规律作专题阐述，以飨读者。

一、定义法求解概率分布与数学期望定义法即根据随机事件的概率、随机变量、概率分布、数学期望的定义求解概率分布与数学期望的方法。

可使用本法解题的考题，一般以古典离散型概率为特征，它可直接利用排列组合的加法原理与乘法原理写出离散型随机变量概率的计算式，进而求得随机变量各值条件下的概率分布与数学期望。

此类题型解题思路明确，利用定义法求解，其方法容易掌握。

例1，（08浙江理）一个袋中装有若干个大小相同的黑球，白球和红球．已知从袋中任意摸出1个球，得到黑球的概率是25；从袋中任意摸出2个球，至少得到1个白球的概率是79． （1）若袋中共有10个球，（1）若袋中共有10个球，（ⅰ）求白球的个数；（ⅱ）从袋中任意摸出3个球，记得到白球的个数为ξ，求随机变量ξ的数学期望E ξ． （2）求证：从袋中任意摸出2个球，至少得到1个黑球的概率不大于710．并指出袋中哪种颜色的球个数最少．分析：本题是以古典概率为题材的高考题，由于从袋中摸球是有回放地摸球，且每次摸球都是互相独立的，系互不影响事件，所发生的概率是等可能的。

故可根据概率定义，利用排列组合计算方法求解随机变量各值的概率。

解：袋中共有10个球，且至少得到1个白球的概率为97，设其中有X 个白球，我们将至少得到一个白球的事件为A ，则P （A ）=97，又∵P （A ）=9721021110=+C C C C x x ，∴9721021110=+C C C C x x ，化简后解之得x=5或14（舍去），∴袋中有5个白球。

概率统计中的概率分布与期望计算概率统计是数学的一个重要分支，它研究的是随机事件的发生规律和概率分布。

在概率统计中，概率分布是描述随机变量可能取值的概率的函数。

而期望则是对随机变量的平均值的度量。

概率分布和期望计算在实际生活和科学研究中有着广泛的应用。

一、概率分布概率分布是描述随机变量可能取值的概率的函数。

常见的概率分布有离散型概率分布和连续型概率分布两种。

离散型概率分布是指随机变量只能取有限个或可列个值的概率分布。

例如，抛硬币的结果可以是正面或反面，这是一个离散型概率分布。

常见的离散型概率分布有伯努利分布、二项分布和泊松分布等。

连续型概率分布是指随机变量可以取任意实数值的概率分布。

例如，测量某物体的长度可以是任意实数值，这是一个连续型概率分布。

常见的连续型概率分布有正态分布、指数分布和均匀分布等。

在实际应用中，我们可以通过观察数据的分布情况来选择合适的概率分布模型。

通过拟合数据，我们可以估计出概率分布的参数，进而进行概率预测和统计推断。

二、期望计算期望是对随机变量的平均值的度量，它表示随机变量的取值在不同取值下的平均值。

期望的计算可以帮助我们了解随机变量的平均水平，从而对随机现象进行预测和分析。

对于离散型随机变量，期望的计算公式为E(X) = ΣxP(X=x)，其中x表示随机变量的取值，P(X=x)表示随机变量取值为x的概率。

通过对所有取值的加权平均，我们可以得到随机变量的期望。

对于连续型随机变量，期望的计算公式为E(X) = ∫xf(x)dx，其中f(x)表示随机变量的概率密度函数。

通过对密度函数的积分，我们可以求得连续型随机变量的期望。

期望的计算在实际应用中有着广泛的应用。

例如，在金融领域，我们可以通过计算股票的期望收益来评估投资风险和回报。

在工程领域，我们可以通过计算设备的平均寿命来进行维护和更新计划。

在医学研究中，我们可以通过计算药物的平均疗效来评估治疗效果。

三、应用实例为了更好地理解概率分布和期望计算的应用，我们举一个实际的例子。

因每个球落入每个盒子是等可能的均为1/M, 所以，对第i 个盒子，一个球不落入这个盒子 内的概率为(1-1/M)。故N个球都不落入这个 盒子内的概率为(1-1/M)n ，即
最常用的数字特征是：期望和方差。
第四章 数字特征
§4.1 数学期望
4.1.1 离散型随机变量的数学期望 概念引入：
某车间对工人生产情况进行考察，车工 小张每天生产的废品数 X 是一个随机变量 。如何定义 X 的平均值？
若统计了100天小张生产产品的情况，发现 ： 32天没有出废品；30天每天出一件废品； 17天每天出两件废品；21天每天出三件废品。
可以得到这n天中，每天的平均废品数为
这是以频率为 权的加权平均
由频率与概率的关系，
不难想到：求废品数X的平 均值时，用概率替代频率， 得平均值为：
这样，就得到一个确定的数
这是以概率为 权的加权平均
——随机变量X的期望(均值) 。
定义1: 设X是离散型随机变量, 概率分布为 P{X=xk}=pk , k=1,2, …。
解：设组织货源 t 吨。显然，应要求
2000≤t ≤4000。国家收益Y(单位:万元)是X
的函数Y=g(X)。表达式为
由已知条件, 知X的概率密度函为
可算得当 t = 3500 时， E(Y)=-2t2 + 14000t-8000000
达到最大值 1.55×106。 因此，应组织3500吨货源。
概率论与数理统计-数学期望_图文.ppt
前面讨论了随机变量及其分布。 如果我 们知道了随机变量 X 的概率分布，那么，关 于 X 的全部概率特征也就知道了。
然而，在实际问题中，概率分布是较难 确定的。且有时在实际应用中，我们并不需 要知道随机变量的所有性质，只要知道其一 些数字特征就够了。

概率分布（数学期望，平均值，方差，标准差）2018展开全文我们已经了解概率的基础，概率中通常将试验的结果称为随机变量。

随机变量将每一个可能出现的试验结果赋予了一个数值，包含离散型随机变量和连续型随机变量。

掷硬币就是一个典型的离散型随机变量，离散随机变量可以取无限个但可数的数值。

而连续变量相反，它在某一个区间内能取任意的数值。

时间就是一个典型的连续变量，1.25分钟、1.251分钟，1.2512分钟，它能无限分割。

既然随机变量可以取不同的值，统计学家就用概率分布描述随机变量取不同值的概率。

相对应的，有离散型概率分布和连续型概率分布。

对于离散型随机变量x，定义一个概率函数叫f(x)，它给出了随机变量取每一个值的概率。

拿出一个骰子，掷到6的概率是f(6) = 1/6，掷到1和6的概率则是f(1)+f(6) = 1/3。

数学期望（均值）理解一：在概率论和统计学中，数学期望(mean)（或均值，亦简称期望）是试验中每次可能结果的概率乘以其结果的总和。

是最基本的数学特征之一。

它反映随机变量平均取值的大小。

其公式如下：xk ：表示观察到随机变量X的样本的值。

pk : 表示xk发生的概率。

数学期望反映的是平均水平。

通过它，我们能够了解一个群体的平均水平（比如说，一个班平均成绩８０）。

但另外一个方面，它所包含的信息也是十分有限的，首先是个体信息被压缩了，其次如果单纯看期望的话，是看不出样本的数量。

（平均成绩为８０，在１人班和１００人班的含义是不一样的）通过这个问题想说明，在刻画群体特征的时候，多个数字特征配合才能达到效果。

（上面的例子：可以是期望 + 数量）理解二：在概率论和统计学中，数学期望(mean)（或均值，亦简称期望）是试验中每次可能结果的概率乘以其结果的总和严格的定义如下：2.数学期望的含义这个很重要，我们一定要明白概念的含义，联系到实际的应用场景中表达的真正意义，数学期望的存在是为了表达什么？答：反映随机变量平均取值的大小3.数学期望（均值）和算术平均值（平均数）的关系（期望和平均数的关系）谈谈我对于这两个概念的理解（1）平均数是根据实际结果统计得到的随机变量样本计算出来的算术平均值，和实验本身有关，而数学期望是完全由随机变量的概率分布所确定的，和实验本身无关。

前两章讨论了随机变量的分布函数，我们看到分布函数能够 完整地描述随机变量的统计特征，但在一些实际问题中，随 机变量的分布函数并不容易求得；另一方面，在一些实际问 题中，我们往往并不直接对分布函数感兴趣，而只对分布的 少数几个特征指标感兴趣，例如分布的中心位置，分散程度 等等，一般称之为随机变量的数字特征，而这些数字特征在 理论和实践中都具有十分重要的意义。本章介绍随机变量的 常用数字特征：数学期望、方差、协方差、相关系数和矩。
第一节 数学期望
单击此处添加副标题
一、离散型随 机变量的数学 期望
汇报日期
我们希望引进这样一个特征数字，它能反 映随机变量X所取数值的集中位置，就象 力学系统中的重心反映该系统质量的集中 位置一样，在概率论中，这样一个数字就 是随机变量的数学期望（也称平均值）. 先看一个例子。
中靶环数(xi) 0 1 2 3 4 5 6 7 8 9 10 频 数(ni) 1 2 1 2 3 3 2 1 2 2 1
0,
0 x,
其它.
E(Y)0sinx1dx2
f(x) 1e1 2x2, x
2
E(例X)10设xfX(x~)dNx (0,1), 求 E(xX)1,E(eX122x2)d.x 0
2解
E( X 2 )
x2 f (x)d x
x2
1
x2
e 2 dx
2
1
x2
xd(e 2 )
2
方法1 先利用分布函数法求得Y的概率密度为
fY (y)
2, 1y2
0 y 1,
0,
其它.
再由公式(2)得
1
E(Y) y
0
12y2dy2
例9 设随机变量X在区间(0,p)内服从均匀分 布，求随机变量函数Y=sinX的数学期望.

高中数学知识点总结概率分布与期望概率分布与期望是高中数学中的重要知识点。

它们在统计学和概率论中起着重要作用。

通过对随机变量的概率分布进行研究，我们可以了解事件发生的可能性以及事件结果的平均值。

本文将对概率分布和期望进行详细讲解，并且通过例题来帮助读者更好地理解和应用这些概念。

一、概率分布概率分布描述了随机变量在每个取值上的概率。

常见的概率分布包括离散概率分布和连续概率分布。

1. 离散概率分布离散概率分布是指随机变量只取有限个或可列个值的概率分布。

在离散概率分布中，每个取值都对应一个概率。

我们可以通过列出随机变量的取值及其对应的概率来描述概率分布。

例题：某餐厅每天的顾客人数服从以下概率分布，求顾客人数的期望值。

顾客人数： 0 1 2 3 4概率： 0.1 0.3 0.4 0.15 0.05解答：期望值的计算公式为E(X) = Σ x * P(X = x)，其中x表示随机变量的取值，P(X = x)表示该取值对应的概率。

根据给定的概率分布，可以计算期望值：E(X) = 0 * 0.1 + 1 * 0.3 + 2 * 0.4 + 3 * 0.15 + 4 * 0.05 = 1.9因此，顾客人数的期望值为1.9。

2. 连续概率分布连续概率分布是指随机变量在某一区间上取值的概率。

在连续概率分布中，我们使用概率密度函数来描述概率分布。

概率密度函数（PDF）有以下性质：非负性、归一性和可积性。

常见的连续概率分布包括均匀分布、正态分布和指数分布等。

这些分布都有各自的概率密度函数，可以根据具体情况进行计算。

二、期望期望是概率分布的一个重要指标，是对随机事件结果的平均值的度量。

它反映了事件结果的集中趋势。

1. 离散随机变量的期望对于离散随机变量X，其期望E(X)的计算公式为E(X) = Σ x * P(X = x)，其中x表示随机变量的取值，P(X = x)表示该取值对应的概率。

2. 连续随机变量的期望对于连续随机变量X，其期望E(X)的计算公式为E(X) = ∫ xf(x) dx，其中f(x)表示X的概率密度函数。

上课材料之三：第二节 分布函数(Distribution function)，数学期望(Expectation)与方差(Variance)本节主要介绍概率及其分布函数，数学期望，方差等方面的基础知识。

一、概率(Probability)1、概率定义(Definition of Probability)在自然界和人类社会中有着两类不同的现象，一类是决定性现象，其特征是在一定条件必然会发生的现象；另一类是随机现象，其特征是在基本条件不变的情况下，观察到或试验的结果会不同。

换句话说，就个别的试验或观察而言，它会时而出现这种结果，时而出现那样结果，呈现出一种偶然情况，这种现象称为随机现象。

随机现象有其偶然性的一面，也有其必然性的一面，这种必然性表现为大量试验中随机事件出现的频率的稳定性，即一个随机事件出现的频率常在某了固定的常数附近变动，这种规律性我们称之为统计规律性。

频率的稳定性说明随机事件发生可能性大小是随机事件本身固定的，不随人们意志而改变的一种客观属性，因此可以对它进行度量。

对于一个随机事件A ，用一个数P （A ）来表示该事件发生的可能性大小，这个数P （A ）就称为随机事件A 的概率，因此，概率度量了随机事件发生的可能性的大小。

对于随机现象，光知道它可能出现什么结果，价值不大，而指出各种结果出现的可能性的大小则具有很大的意义。

有了概率的概念，就使我们能对随机现象进行定量研究，由此建立了一个新的数学分支——概率论。

概率的定义定义在事件域F 上的一个集合函数P 称为概率，如果它满足如下三个条件： （i ）P （A ）≥0，对一切∈A F （ii ）P （Ω）=1；（iii ）若∈i A ，i=1,2…，且两两互不相容，则∑∑∞=∞==⎪⎭⎫ ⎝⎛11)(i i i i A P A P 性质（iii ）称为可列可加性（conformable addition ）或完全可加性。

推论1：对任何事件A 有)(1)(A P A P -=；推论2：不可能事件的概率为0，即0)(=φP ； 推论3：)()()()(AB P B P A P B A P -+=⋃。

定义1 设X是离散型随机变量，它的分布律是:
如果 | xk | pk 有限,定义X的数学期望
k 1

P(X=xk)=pk , k=1,2,…

E ( X ) xk pk
k 1
也就是说,离散型随机变量的数学期望是一个 绝对收敛的级数的和.
分赌本问题 A 期望所得的赌金即为 X 的数学期望
因此彩票发行单位发行 10 万张彩票的创收利 润为
击中环数 概率 击中环数 概率 8 9 10
0 . 3 0 .1 0 . 6
8 9 10
乙射手
0 .2 0 .5 0 .3
试问哪个射手技术较好?
解 设甲、乙射手射中的环数分别为 X 1 , X 2 . 甲射手
击中环数 概率 8 9 10
0 . 3 0 .1 0 . 6
E ( X 1 ) 8 0.3 9 0.1 10 0.6 9.3(环),
200
即为 X 的可能值与其概率之积的累加.
引例2 射击问题 设某射击手在同样的条件下, 瞄准靶子相继射击90次,(命中的 环数是一个随机变量).射中次数 记录如下 命中环数 k 0 1 2 3
命中次数 nk
2 13 15
4 20
5
10
30
2 13 15 nk 10 20 30 频率 90 90 90 n 90 90 90 试问:该射手每次射击平均命中靶多少环?
1 3 200 0 4 4
50(元).
若设随机变量 X 为:在 A 胜2局 B 胜1局 的前提下, 继续赌下去 A 最终所得的赌金.
0 3 1 其概率分别为: 4 4 因而A期望所得的赌金即为X的 “期望”值, 3 1 200 0 150(元). 等于 4 4

E[ X i ] E( X i )
i 1 i 1 n n
请注意: 由E(XY)=E(X)E(Y) 不一定能推出X,Y 独立
4. 设X、Y 相互独立，则 E(XY)=E(X)E(Y);
E[ X i ] E ( X i ) （诸Xi相互独立时）
i 1 i 1
n
n
三、数学期望的性质
计算t的值使得EY 达到最大 t ( EY ) 7 0 t 3500 t 500 即组织货源3500吨为宜.
二、连续型随机变量的数学期望
综上：
xi pi , X 离散型 i 1 EX xf ( x )dx , X 连续型
发散，则称X的数学
二、连续型随机变量的数学期望
关于定义的两点说明 (1)连续型随机变量X的数学期望为实数域R上 对取值与密度值乘积的广义积分. (2)注意区分： xf ( x)dx E ( X )




f ( x)dx 1
二、连续型随机变量的数学期望
x2 0 x1 f ( x ) 2 x 1 x 2，求EX . 0 其它
15 40 30 10 5 18 19 20 21 22 100 100 100 100 100
18 15% 19 40% 20 30% 2110% 22 5%
—各年龄出现的频率 将此种方法下计算的平均年龄称为依频率的加权平均。
例如：评价地区粮食水平，只需了解粮食的平 均产量；评价棉花质量，既要注意纤维的平均长度， 又要注意个体真实长度与平均长度的总体偏差程度， 一般认为，平均长度越长，整体偏差越小，质量就 越好。 因此，在对随机变量的研究中，确定某些数字 特征是重要的 . 常用的数字特征：数学期望，方差.

概率分布与期望的计算方法概率分布和期望是概率论中两个基本且重要的概念，它们在统计学、物理学、工程学、生物学等领域都有广泛应用。

概率分布是研究随机变量取得各种可能取值的概率分布情况，而期望则是指数学上的数学期望，是所有可能取值的加权平均值。

本文将介绍概率分布和期望的计算方法。

一、概率分布的计算方法1. 离散型随机变量概率分布的计算方法离散型随机变量是一种取有限个或可数个值的随机变量，如抛掷骰子的点数、抽取彩球的颜色等。

离散型随机变量的概率分布可以用概率分布函数、概率质量函数和累积分布函数等方法计算。

概率分布函数（Probability Mass Function，简称PMF）是指随机变量X取某个具体值的概率。

公式如下：P(X=x)=p其中，p表示X取值为x的概率。

例如，一枚硬币正面朝上的概率为0.5，反面朝上的概率为0.5，其PMF如下：P(X=正) = 0.5P(X=反) = 0.5概率质量函数（Probability Density Function，简称PDF）是离散型随机变量的概率分布函数，表示随机变量取某个具体值的概率密度。

公式如下：f(x)=P(X=x)其中，f(x)表示X取值为x的概率密度。

例如，一次投掷一个骰子，其点数的PDF如下：点数 1 2 3 4 5 6概率1/6 1/6 1/6 1/6 1/6 1/6累积分布函数（Cumulative Distribution Function，简称CDF）是指随机变量X小于等于某个具体值a的概率。

公式如下：F(a)=P(X≤a)例如，一次投掷一个骰子，其点数的CDF如下：点数 1 2 3 4 5 6概率1/6 2/6 3/6 4/6 5/6 6/62. 连续型随机变量概率分布的计算方法连续型随机变量是一种取无限个值的随机变量，如测量某物理量的误差、抽取某种材料的密度等。

连续型随机变量的概率分布可以用概率密度函数和累积分布函数等方法计算。

概率密度函数（Probability Density Function，简称PDF）是指随机变量X取某个具体值的概率密度，而不是概率。