最新摄影测量学教案(第13讲空间前方交会)doc讲课教案

课程编号：1300358课程类别：必修授课对象：摄影测量专业授课时间：1周教学目标：1. 使学生掌握摄影测量学的基本概念、原理和方法。

2. 理解摄影测量在测绘、地理信息系统、工程等领域中的应用。

3. 培养学生独立完成摄影测量任务的能力。

教学内容：一、摄影测量学概述1. 摄影测量学的定义和任务2. 摄影测量学的发展历史3. 摄影测量学的应用领域二、摄影测量基本原理1. 摄影几何原理2. 摄影测量坐标系3. 摄影测量基本方程三、摄影测量方法1. 模拟摄影测量2. 解析摄影测量3. 数字摄影测量四、摄影测量数据处理1. 影像处理2. 像点量测3. 空中三角测量五、摄影测量应用实例1. 地形测绘2. 城市规划3. 工程测量教学过程：第一周：1. 课堂导入：介绍摄影测量学的基本概念、任务和发展历史，激发学生的学习兴趣。

2. 讲解摄影测量基本原理，包括摄影几何原理、摄影测量坐标系和摄影测量基本方程。

3. 讲解摄影测量方法，包括模拟摄影测量、解析摄影测量和数字摄影测量。

4. 课堂练习：布置相关习题，让学生巩固所学知识。

第二周：1. 讲解摄影测量数据处理，包括影像处理、像点量测和空中三角测量。

2. 课堂演示：通过实际案例展示摄影测量数据处理过程。

3. 讲解摄影测量应用实例，包括地形测绘、城市规划和工程测量。

4. 课堂讨论：引导学生讨论摄影测量在实际应用中的优势与挑战。

教学评价：1. 课堂表现：观察学生在课堂上的参与程度，评价学生的积极性。

2. 作业完成情况：检查学生完成课后习题的情况，评价学生对知识的掌握程度。

3. 课堂讨论：评价学生在课堂讨论中的表现，包括发言质量、思维深度等。

教学资源：1. 教材：《摄影测量学》2. 教学课件3. 摄影测量软件4. 摄影测量案例教学反思：1. 关注学生的个体差异，针对不同学生的特点进行差异化教学。

2. 结合实际案例，提高学生的实践能力。

3. 注重培养学生的创新思维和团队合作精神。

摄影测量学教案范文一、教学目标1.了解摄影测量学的基本概念和原理。

2.掌握摄影测量学中的测量方法和技术。

3.能够运用摄影测量学进行实际测量和数据处理。

4.培养学生的观察和判断能力，提高解决问题的能力。

二、教学内容1.摄影测量学的概述A.摄影测量学的定义B.摄影测量学的应用领域2.摄影测量学的基本原理A.相对定向原理B.绝对定向原理C.导线测量原理3.相对定向方法A.特征点法B.控制点法C.地形点法4.绝对定向方法A.双差法B.高程解算C.复查定向5.摄影测量数据处理A.影像图像预处理B.特征点提取C.坐标计算和平差D.结果展示和分析6.摄影测量的误差和精度控制A.摄影测量误差类型及控制方法B.摄影测量精度评定方法7.摄影测量在地图制图中的应用A.比例尺的确定B.三角测量的实施C.地图投影的处理三、教学方法1.讲授法：通过讲述理论知识，让学生了解摄影测量学的基本概念和原理。

2.实验法：安排实际测量任务，训练学生进行测量和数据处理。

3.讨论法：组织学生进行小组讨论，共同解决问题，提高思维能力和解决问题的能力。

4.实例分析法：通过分析实际案例，让学生学会运用摄影测量学解决实际问题。

四、教学过程1.摄影测量学的概述A.讲解摄影测量学的定义和应用领域。

B.给学生分发相关的学习资料。

2.摄影测量学的基本原理A.讲解相对定向原理、绝对定向原理和导线测量原理的基本概念和方法。

B.在黑板上绘制示意图，让学生理解原理。

3.相对定向方法A.讲解特征点法、控制点法和地形点法的基本原理和实施方法。

B.运用实例进行讲解和分析。

4.绝对定向方法A.讲解双差法、高程解算和复查定向的原理和步骤。

B.运用实例进行讲解和分析。

5.摄影测量数据处理A.讲解影像图像预处理、特征点提取、坐标计算和平差的方法和技术。

B.进行实际数据处理的实验，让学生亲自操作和实践。

6.摄影测量的误差和精度控制A.讲解摄影测量的误差类型和控制方法。

B.讲解摄影测量精度评定的方法和标准。

中南大学本科生课程设计（实践）任务书、设计报告（摄影测量与遥感概论）题目：空间后方交会-前交院系：地球科学与信息物理学院班级：测绘1201班********学号：***********名：***二零一四年十一月一、实验目的通过对数字影像空间后交前交的程序设计实验，要求我们进一步理解和掌握影像外方位元素的有关理论、原理和方法。

利用计算机程序设计语言编写摄影测量空间交会软件进行快速确定影响的外方位元素及其精度，然后通过求得的外方位元素求解位置点的地面摄影测量坐标，达到通过摄影测量量测地面地理坐标的目的。

二、实验要求1.用C、VB、C++或MA TLAB语言编写空间后方交会-空间前方交会程序2.提交实习报告：程序框图、程序源代码、计算结果、体会3.计算结果：像点坐标、地面坐标、单位权中误差、外方位元素及其精度4.完成时间：11月11日前完成三、实验数据四、实验思路➢利用后方交会得出两张相片各自的外方位元素1）获取已知数据影响比例尺m,，内方位元素x0 、y0 、f ，控制点的地面摄影测量坐标Xtp, Ytp, Ztp2）量测控制点左片和右片的像点坐标 x，y3）确定未知数初值 Xs0, Ys0, Zs0, ω，φ，κ（线元素可用控制点均值代替，角元素可用0初始化），即：∑=Xtp X 41s0，∑=Ytp Y 41s0，f Z *m s =ω=0，φ=0，κ=0 4）计算旋转矩阵R5）利用共线方程逐点计算像点坐标的近似值 6）组成误差方程式并法化 7）解求外方位元素改正数8）检查迭代是否收敛（改正值是否小于某一特定常数） ➢ 利用解出的外方位元素进行前方交会1）获取已知数据x0 , y0 , f, XS1, YS1, ZS1,φ1,ω1,κ1 , XS2, YS2, ZS2，φ2，ω2，κ22）量测像点坐标 x1,y1 ,x2,y23）由外方位线元素计算基线分量BX, BY, BZ4）由外方位角元素计算像空间辅助坐标 X1, Y1, Z1 , X2, Y2, Z2 5）计算点投影系数 N1 , N2 6）计算地面坐标 XA, YA, ZA五、实验过程➢ 程序流程图此过程完成空间后方交会求解像片的外方位元素，其中改正数小于限差（0.00003，相当于0.1的角度值）为止。

实验一1 实验任务理解摄影测量中核心模型-共线方程作用，掌握航空影像中重要的点线面的透视关系以及物方与像方之间的解析关系，单幅影像上像点坐标与相应地面点坐标之间的关系。

通过编程实现外方位元素的求解，提升编程能力。

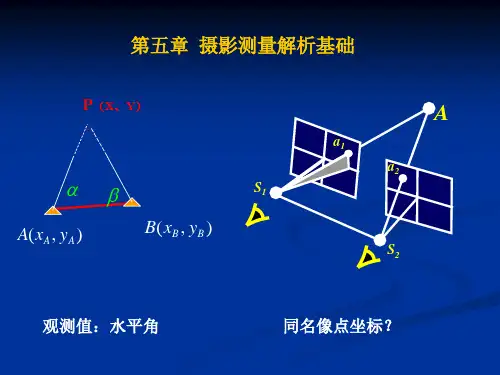
2 理论模型与方法单张像片的空间后方交会的基本思想：以单幅影像为基础，从该影像所覆盖地面范围内若干控制点的已知地面坐标和相应的像坐标量测值处发，根据共线条件方程，解求该影像在航空摄影时刻的元素S X ,S Y ,S Z ,φ,ω,κ。

（1）共线方程)()()()()()()()()()()()(33322203331110S A S A S A S A S A S AS A S A S A S A S A S A Z Z c Y Y b X X a Z Z c Y Y b X X a f y y Z Z c Y Y b X X a Z Z c Y Y b X X a fx x -+-+--+-+--=--+-+--+-+--=-（2）旋转矩阵R123123123cos cos sin sin sin cos sin sin sin cos sin cos cos sin cos cos sin sin cos cos sin sin sin sin cos sin cos cos cos a a a b b b c c c φκφωκφκφωκφωωκωκωφκφωκφκφωκφω=-=--=-===-=+=-+=（3）经过线性化，得到x ，y 的误差方程式yx a a a Z a Y a X a x x a a a Z a Y a X a s s s y s s s x -+∆+∆+∆+∆+∆+∆=-+∆+∆+∆+∆+∆+∆=)(v )(v 262524232221161514131211κφφκφφ矩阵形式如下： L AX V -= 系数方程⎥⎦⎤⎢⎣⎡=262524232221161514131211a a a a a a a a a a a aAxa y x f y f a f y x f y x a ya y x f x f a f y x f x y a Zy c f c a Z y b f b a Z y a f a a Z x c f c a Z x b f b a Z x a f a a -=---=----==+--=+--=+=+=+=+=+=+=262524161514322332223221311331123111)cos sin (/cos cos ]sin )sin cos (/[sin ]cos sin [/sin cos }cos ]sin cos [/{sin /][/][/][/][/][/][κκκωκκκωκκκωκκκω[]Ty y x x L --=)(,)()()()()()()()()()(333222111S S S S S S S S S Z Z c Y Y b X X a Z Z Z c Y Y b X X a Y Z Z c Y Y b X X a X -+-+-=-+-+-=-+-+-= 近似值计算公式如下：ZY f y y Z X f x x //00-=--=-（4）由最小二乘间接平差原理可得：[]κωφ∆∆∆∆∆∆=SSSZ Y X XL A A A X T T 1)(-=+∆+∆+=+∆+∆+=+∆+∆+=+∆+∆+=+∆+∆+=+∆+∆+=2102102102121210κκκκωωωωϕϕϕϕS S S S S S S S S S S S Z Z Z Z Y Y Y Y X X X X 3 程序设计本地方仅列出核心代码： %确定初值 x0=0;f=153.24;m=sqrt(((x(1)-x(2))^2+(y(1)-y(2))^2))/(sqrt(((X(1)-X(2))^2+(Y(1)-Y(2))^2)));Zs=f/m;%3个线性元素Xs=mean(X);Ys=mean(Y);aa=0; %3个外方位角元素初值ww=0;kk=0;cx=zeros(6,1);p=0.1/206264.806247096363;%将0.1秒限差化为弧度aa1=1;ww1=1;kk1=1;k=0;while abs(aa-aa1)>p||abs(ww-ww1)>p||abs(kk-kk1)>paa1=aa;%赋值ww1=ww;kk1=kk;%计算旋转矩阵a1=cos(aa)*cos(kk)-sin(aa)*sin(ww)*sin(kk);a2=-cos(aa)*sin(kk)-sin(aa)*sin(ww)*cos(kk);a3=-sin(aa)*cos(ww);b1=cos(ww)*sin(kk);b2=cos(ww)*cos(kk);b3=-sin(ww);c1=sin(aa)*cos(kk)+cos(aa)*sin(ww)*sin(kk);c2=-sin(aa)*sin(kk)+cos(aa)*sin(ww)*cos(kk);c3=cos(aa)*cos(ww);R=[a1 a2 a3;b1 b2 b3;c1 c2 c3];%计算误差方程系数for i=1:d1%计算近似值XX=a1*(X(i)-Xs)+b1*(Y(i)-Ys)+c1*(Z(i)-Zs);YY=a2*(X(i)-Xs)+b2*(Y(i)-Ys)+c2*(Z(i)-Zs);ZZ=a3*(X(i)-Xs)+b3*(Y(i)-Ys)+c3*(Z(i)-Zs);a11=(1/ZZ)*(a1*f+a3*(x(i)-x0));a12=(1/ZZ)*(b1*f+b3*(x(i)-x0));a13=(1/ZZ)*(c1*f+c3*(x(i)-x0));a14=(y(i)-y0)*sin(ww)-(((x(i)-x0)/f)*((x(i)-x0)*cos(kk)-(y(i)-y0)*sin(kk))+f*cos(kk))*cos(ww);a15=-f*sin(kk)-((x(i)-x0)/f)*((x(i)-x0)*sin(kk)+(y(i)-y0)*cos(kk));a16=(y(i)-y0);a21=(1/ZZ)*(a2*f+a3*(y(i)-y0));a22=(1/ZZ)*(b2*f+b3*(y(i)-y0));a23=(1/ZZ)*(c2*f+c3*(y(i)-y0));a24=-(x(i)-x0)*sin(ww)-(((y(i)-y0)/f)*((x(i)-x0)*cos(kk)-(y(i)-y0)*sin(kk))-f*sin(kk))*cos(ww);a25=-f*cos(kk)-((y(i)-y0)/f)*((x(i)-x0)*sin(kk)+(y(i)-y0)*cos(kk));a26=-(x(i)-x0);A(2*i-1,:)=[a11 a12 a13 a14 a15 a16];A(2*i,:)=[a21 a22 a23 a24 a25 a26];l(2*i-1,:)=x(i)-(x0-f*XX/ZZ);l(2*i,:)=y(i)-(y0-f*YY/ZZ);endcx1=inv(A'*A)*A'*l;%最小二乘平差Xs=Xs+cx1(1);Ys=Ys+cx1(2);Zs=Zs+cx1(3);aa=aa+cx1(4);ww=ww+cx1(5);kk=kk+cx1(6);k=k+1;%统计循环次数endV==A*cx1-l;sigma=sqrt(V'*V/11);4 结论与体会本次实验使用了一种相对比较简单的MATLAB语言来编写外方位元素求解，总体来说，过程比较简单，但是在数据检验方面经常不不符，追其根源是在代码书写过程中错误太多，导致结果不对。