摄影测量学教案(第13讲空间前方交会).doc

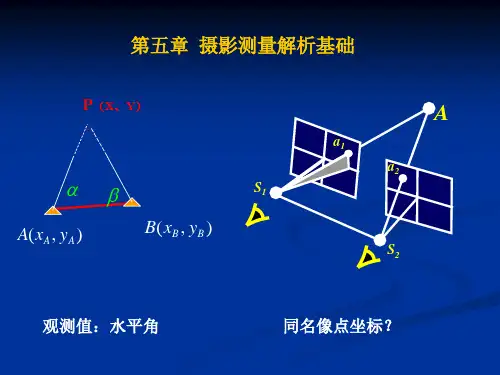
空间后交—前交程序设计(实验报告)姓名：班级：学号：时间:空间后交-前交程序设计一、实验目的用 C 、VB或MATLAB语言编写空间后方交会-空间前方交会程序⑴提交实习报告：程序框图、程序源代码、计算结果、体会⑵计算结果：像点坐标、地面坐标、单位权中误差、外方位元素及其精度二、实验数据f=150。

000mm，x0=0，y0=0三、实验思路1。

利用空间后方交会求左右像片的外方位元素(1）.获取m（于像片中选取两点，于地面摄影测量坐标系中选取同点,分别计算距离，距离比值即为m)，x，y，f,X，Y,Z（2).确定未知数初始值Xs,Ys，Zs,q，w,k（3）.计算旋转矩阵R(4）.逐点计算像点坐标的近似值(x），（y）(5）。

组成误差方程式(6)。

组成法方程式（7).解求外方位元素（8）。

检查是否收敛，即将求得的外方位元素的改正数与规定限差比较，小于限差即终止；否则用新的近似值重复步骤(3）-（7）2。

利用求出的外方位元素进行空间前交，求出待定点地面坐标(1）.用各自像片的角元素计算出左、右像片的方向余弦值，组成旋转矩阵R1，R2(2）。

根据左、右像片的外方位元素，计算摄影基线分量Bx，By，Bz(3)。

计算像点的像空间辅助坐标（X1,Y1，Z1）和（X2，Y2,Z2）（4）.计算点投影系数N1和N2(5）。

计算未知点的地面摄影测量坐标四、实验过程⑴程序框图函数AandL%求间接平差时需要的系数％%％已知％a=像点坐标x，b=像点坐标y,f内方位元素主距%φ=q，ψ=w，κ=k%像空间坐标系X,Y，Z%地面摄影测量坐标系Xs,Ys,Zsfunction ［A1，L1，A2，L2］=AandL（a，b，f,q,w,k,X，Y，Z,Xs,Ys,Zs) %％％％％%％％%%％选择矩阵元素a1=cos（q)＊cos(k)—sin(q）＊sin(w）*sin(k）;a2=-cos(q)＊sin(k)—sin(q）＊sin(w）＊cos（k)；a3=-sin(q）*cos(w);b1=cos(w）*sin(k)；b2=cos（w）*cos（k)；b3=—sin(w);c1=sin（q)*cos(k)+cos（q)＊sin(w）*sin（k)；c2=—sin（q）＊sin(k)+cos（q)*sin(w）*cos（k)；c3=cos(q)＊cos(w);％%％%％％％共线方程的分子分母X_=a1*(X—Xs）+b1*（Y-Ys)+c1＊（Z-Zs);Y_=a2*(X-Xs)+b2＊（Y—Ys)+c2＊（Z-Zs);Z_=a3＊(X—Xs)+b3＊（Y—Ys）+c3*(Z-Zs）;％％％％%％%近似值x=-f＊X_/Z_；y=-f＊Y_/Z_;％％％％%％％A组成L组成a11=1/Z_＊（a1＊f+a3＊x)；a12=1/Z_＊(b1＊f+b3＊x）；a13=1/Z_*(c1*f+c3＊x);a21=1/Z_*(a2＊f+a3＊y）;a22=1/Z_*（b2＊f+b3*y);a23=1/Z_＊(c2＊f+c3＊y）;a14=y*sin（w)-（x/f＊(x*cos(k)—y*sin（k））+f＊cos（k）)*cos(w）;a15=-f*sin(k)—x/f＊（x*sin（k）+y*cos(k));a16=y；a24=—x*sin(w）-（y/f＊（x*cos(k)-y*sin(k)）—f＊sin(k））*cos（w）；a25=-f*cos（k）-y/f*(x*sin（k）+y*cos(k));a26=-x;lx=a—x；ly=b-y;％%%%%%％％%组成一个矩阵，并返回A1=[a11,a12，a13,a14,a15，a16];A2=［a21,a22,a23，a24,a25，a26];L1=lx;L2=ly;函数deg2dms％%％%％%％％角度转度分秒function y=deg2dms(x）a=floor(x)；b=floor(（x-a)＊60);c=(x-a—b/60）＊3600；y=a+（b/100）+(c/10000);函数dms2deg%%％％%度分秒转度function y=dms2deg（x）a=floor(x）；b=floor((x-a)＊100）；c=（x-a—b/100)*10000；y=a+b/60+c/3600;函数ok%％％％％%%％%%%％％％目的是为了保证各取的值的有效值%％xy为n*1，a为1＊nfunction result=ok(xy，a)format short gi=size（xy，1)；for n=1:io=xy（n)—floor(xy(n,1));o=round（o＊（10^a（n))）/(10^a(n）);xy(n，1)=floor(xy（n,1）)+o;endformat long gresult=xy;函数rad2dmsxy%%％%求度分秒表现形式的三个外方位元素，三个角度function xydms=rad2dmsxy(xy)［a,b,c，d，e,f]=testvar(xy）;d=deg2dms（rad2deg(d））；e=deg2dms（rad2deg(e))；f=deg2dms(rad2deg(f）);xydms=[a,b，c,d,e，f］';函数spacehoujiao％％%％%%%空间后交％%% f%％输入p（2*n,1）%％像点坐标x,y,X,Y，Z,均为（n,1）function ［xy,m，R］=spacehoujiao(p，x,y，f,X，Y,Z）format long；%%％%％权的矢量化,这是等精度时的，如果非,将函数参数改为PP=diag（p)；％％求nj=size（X，2）；%％初始化Xs=0；Ys=0;Zs=0;for n=1：jXs=Xs+X（n）；Ys=Ys+Y(n）;Zs=Zs+Z(n）;endSx=sqrt((x（2）-x(1）)^2+(y（2)—y(1)）^2);％%％%两像点之间距离Sd=sqrt(（X(2）-X（1))^2+(Y（2）-Y（1))^2);%％%％两地面控制点之间距离m=Sd/Sx; ％％％％图像比例系数Xs=Xs/j;Ys=Ys/j;Zs=m*f+Zs/j；m0=0;q=0;w=0;k=0;i=0;a=rand(2*j,6）；l=rand（2＊j，1);％％％％for n=1:j[a（2＊n—1,:)，l(2*n—1,1）,a(2＊n,：），l(2*n,1）］=AandL(x(n)，y（n),f,q，w，k，X(n)，Y（n），Z(n），Xs,Ys,Zs);enddet=inv（a’＊P*a）*transpose（a)*P*l;％%%%%%％％％循环体while 1％％％％％%%％%％％％％%％％[dXs,dYs,dZs，dq,dw,dk]=testvar(det）;detXs=abs（dXs）；detYs=abs（dYs)；detZs=abs(dZs)；detq=abs(dq)；detw=abs（dw)；detk=abs（dk)；%%％％%%％%%if （（detXs<0。

《摄影测量学》教学大纲一、课程基本信息1．课程代码：211288002．课程中文名称：摄影测量学课程英文名称：Photography Surveying A3．面向对象：测绘工程专业的学生4．开课学院（课部）、系（中心、室）：信息工程学院测绘工程系5．总学时数：56讲课学时数：48，实验学时数：86．学分数：3.57．授课语种：汉语，考试语种：汉语8．教材：王佩军，徐亚明编著，《摄影测量学》，武汉大学出版社二、课程内容简介本课程主要内容可划分为基础知识即解析摄影测量、数字摄影测量及外业三部分。

其中解析部分主要包括摄影基本知识、单张航摄像片解析、像片立体观察与量测、双像解析摄影测量以及解析空中三角测量几个方面，学生学习本部分内容应达到以下要求：1、摄影测量学的定义与分类（1）掌握摄影测量的定义、分类、平台、特点和任务；（2）掌握摄影测量三个发展阶段的基本特点；2、摄影基本知识（1）了解摄影原理与摄影机类型、基本构造；（2）了解摄影处理与像片的晒印过程；（3）了解航空摄影与摄影测量对摄影的基本要求；（4）掌握像片影像的系统误差类型及处理；（5）了解彩色摄影与其它摄影方式。

3、单张航摄像片解析（1）了解中心投影的基本知识；（2）掌握摄影测量中常用坐标系的三轴定义及用途；（3）掌握航摄像片的内、外方位元素；（4）掌握像点在空间直角坐标系中的变换过程；（5）掌握中心投影的构像方程的推导，了解其应用；（6）掌握像点位移的类型及其规律；（7）掌握单张像片空间后方交会的基本原理与解算步骤。

4、像片立体观察与量测（1）了解人眼的立体视觉原理；（2）了解人造立体视觉原理及产生的条件；（3）掌握像对的立体观察方法；（4）掌握像对的立体量测步骤；（5）了解像点坐标量测仪器。

5、双像解析摄影测量（1）了解双像解析摄影测量的方法；（2）掌握立体像对空间前方交会的原理与过程；（3）掌握空间后方交会与前方交会求解地面点坐标的计算方法；（4）掌握连续法解析相对定向及模型坐标计算过程；（5）掌握立体模型的绝对定向过程；（6）掌握光束法整体解求的原理。

摄影测量实验报告（空间后⽅交会—前⽅交会）空间后⽅交会-空间前⽅交会程序编程实验⼀．实验⽬的要求掌握运⽤空间后⽅交会-空间前⽅交会求解地⾯点的空间位置。

学会运⽤空间后⽅交会的原理，根据所给控制点的地⾯摄影测量坐标系坐标以及相应的像平⾯坐标系中的坐标，利⽤计算机编程语⾔实现空间后⽅交会的过程，完成所给像对中两张像⽚各⾃的外⽅位元素的求解。

然后根据空间后⽅交会所得的两张像⽚的内外⽅位元素，利⽤同名像点在左右像⽚上的坐标，求解其对应的地⾯点在摄影测量坐标系中的坐标，并完成精度评定过程，利⽤计算机编程语⾔实现此过程。

⼆．仪器⽤具计算机、编程软件（MATLAB）三．实验数据实验数据包含四个地⾯控制点（GCP）的地⾯摄影测量坐标及在左右像⽚中的像平⾯坐标。

此四对坐标运⽤最⼩⼆乘法求解左右像⽚的外⽅位元素，即完成了空间后⽅的过程。

另外还给出了5对地⾯点在左右像⽚中的像平⾯坐标和左右像⽚的内⽅位元素。

实验数据如下：内⽅位元素：f=152.000mm，x0=0，y0=0四．实验框图此过程完成空间后⽅交会求解像⽚的外⽅位元素，其中改正数⼩于限差（0.00003，相当于0.1’的⾓度值）为⽌。

在这个过程中采⽤迭代的⽅法，是外⽅位元素逐渐收敛于理论值，每次迭代所得的改正数都应加到上⼀次的初始值之中。

确定Xs，Ys，Zs的初始值时，对于左⽚可取地⾯左边两个GCP的坐标的平均值作为左⽚Xs 和Ys的初始值，取右边两个GCP 的坐标平均值作为右⽚Xs 和Ys的初始值。

Zs可取地⾯所有GCP的Z坐标的平均值再加上航⾼。

空间前⽅交会的数学模型为：五．实验源代码function Main_KJQHFJH()global R g1 g2 m G a c b1 b2;m=10000;a=5;c=4;feval(@shuru); %调⽤shuru（）shurujcp（）函数完成像点及feval(@shurujcp); %CCP有关数据的输⼊XYZ=feval(@MQZqianfangjh); %调⽤MQZqianfangjh（）函数完成空间前⽅、%%%%%% 单位权中误差%%%% %后⽅交会计算解得外⽅位元素global V1 V2; %由于以上三个函数定义在外部⽂件中故需VV=[]; %⽤feval（）完成调⽤过程for i=1:2*cVV(i)=V1(i);VV(2*i+1)=V2(i);endm0=sqrt(VV*(VV')/(2*c-6));输⼊GCP像点坐标及地⾯摄影测量坐标系坐标的函数和输⼊所求点像点坐标函数：function shurujcp()global c m;m=input('摄影⽐例尺：'); %输⼊GCP像点坐标数据函数并分别将其c=input('GCP的总数='); % 存⼊到不同的矩阵之中disp('GCP左⽚像框标坐标：');global g1;g1=zeros(c,2);i=1;while i<=cm=input('x=');n=input('y=');g1(i,1)=m;g1(i,2)=n;i=i+1;enddisp('GCP右⽚像框标坐标：');global g2;g2=zeros(c,2);i=1;while i<=cm=input('x=');n=input('y=');g2(i,1)=m;g2(i,2)=n;i=i+1;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function shuru()global a;a=input('计算总像对点数='); %完成想计算所需的像平⾯坐标global b1; %坐标输⼊，存⼊不同的矩阵中b1=zeros(a,2); disp('左⽚像点坐标：')i=1;while i<=am=input('x=');n=input('y=');b1(i,1)=m;b1(i,2)=n;i=i+1;end%%b2=zeros(a,2);disp('右⽚像点坐标：')i=1;while i<=am=input('x=');n=input('y=');b2(i,1)=m;b2(i,2)=n;i=i+1;end%%global c;c=input('GCP的总数=');disp('GCP摄影测量系坐标：')global G;G=zeros(3,c);i=1;while i<=cm=input('X=');n=input('Y=');v=input('Z=');G(i,1)=m;G(i,2)=n;G(i,3)=v;i=i+1;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%空间前⽅交会和后⽅交会函数：function XYZ=MQZqianfangjh()global R1 R2 a f b1 b2 Ra Rb;global X1 X2;R1=Ra;R2=Rb;R1=zeros(3,3);R2=zeros(3,3);global g1 g2 G V1 V2 V WF c QXX QXX1 QXX2;xs0=(G(1,1)+G(3,1))/2;ys0=(G(1,2)+G(3,2))/2;[Xs1,Ys1,Zs1,q1,w1,k1 R]=houfangjh(g1,xs0,ys0); %对左⽚调⽤后⽅交会函数R1=R;V1=V;WF1=WF;save '左⽚外⽅位元素为.txt' WF -ascii %将计算所得的外⽅位元素存⼊到.txt% ⽂件中for i=1:cg1(i,1)=g1(i,1)+V1(2*i-1);g1(i,2)=g1(i,2)+V1(2*i);endsave '左⽚像点坐标.txt' g1 -asciixs0=(G(2,1)+G(4,1))/2;ys0=(G(2,2)+G(4,2))/2;[Xs2,Ys2,Zs2,q2,w2,k2 R]=houfangjh(g2,xs0,ys0); %对右⽚调⽤后⽅交会函数R2=R; V2=V;WF2=WF;QXX2=QXX;save '右⽚外⽅位元素为.txt' WF –ascii %将计算所得的外⽅位元素存⼊到.txt% ⽂件中for i=1:cg2(i,1)=g2(i,1)+V2(2*i-1);g2(i,2)=g2(i,2)+V2(2*i);endsave '右⽚像点坐标.txt' g2 -asciiX1=zeros(a,3);X2=zeros(a,3);xx=zeros(3,1);xxx=zeros(3,1);for i=1:ass=[b1(i,1);b1(i,2);-f];dd=[b2(i,1);b2(i,2);-f];xx=R1*ss;X1(i,:)=xx';xxx=R2*dd;X2(i,:)=xxx';endglobal Xs1 Xs2 Ys1 Ys2 Zs1 Zs2;BX=Xs2-Xs1;BY=Ys2-Ys1;BZ=Zs2-Zs1;global N1 N2;N1=zeros(1,a);N2=zeros(1,a);for i=1:aN1(1,i)=(BX*X2(i,3)-BZ*X2(i,1))/(X1(i,1)*X2(i,3)-X2(i,1)*X1(i,3));N2(1,i)=(BX*X1(i,3)-BZ*X1(i,1))/(X1(i,1)*X2(i,3)-X2(i,1)*X1(i,3));end %计算投影系数，并计算五点的三维坐标global XYZ;XYZ=zeros(a,3);for i=1:aXYZ(i,1)=Xs1+N1(1,i)*X1(i,1);XYZ(i,2)=((Ys1+N1(1,i)*X1(i,2))+(Ys2+N2(1,i)*X2(i,2)))/2;enddisp('左⽚外⽅位元素为:Xs Ys Zs ψωκ');disp(WF1);disp('左⽚外⽅位元素协因素阵为：');disp(QXX1);disp('左⽚像点坐标为：')disp(g1)disp('右⽚外⽅位元素为:Xs Ys Zs ψωκ');disp(WF2);disp('右⽚外⽅位元素协因素阵为：')disp(QXX2)disp('右⽚像点坐标为：')disp(g2)disp('计算所得点摄影测量坐标（X,Y,Z）为：');disp(XYZ);save 'XYZ.txt' XYZ -ascii %将计算所得结果保存到XYZ.txt⽂件中%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function [Xs,Ys,Zs,q,w,k R]=houfangjh(g1,Xs0,Ys0) %计算像⽚外⽅位元素%%%%%%%%%%global f G m c b1 b2;f=0.152;Xs=Xs0;Ys=Ys0;Zs=m*f+G(1,3);q=0;w=0;k=0;while 1 %实现⼀个永真循环，是改正数⼩于限差以后跳出循环a1=cos(q)*cos(k)-sin(q)*sin(w)*sin(k);a2=-cos(q)*sin(k)-sin(q)*sin(w)*cos(k);a3=-sin(q)*cos(w);b1_=cos(w)*sin(k);b2_=cos(w)*cos(k);b3=-sin(w);c1=sin(q)*cos(k)+cos(q)*sin(w)*sin(k);c2=-sin(q)*sin(k)+cos(q)*sin(w)*cos(k);c3=cos(q)*cos(w);R=[a1,a2,a3;b1_,b2_,b3;c1,c2,c3];for i=1:caX(i)=a1*(G(i,1)-Xs)+b1_*(G(i,2)-Ys)+c1*(G(i,3)-Zs);aY(i)=a2*(G(i,1)-Xs)+b2_*(G(i,2)-Ys)+c2*(G(i,3)-Zs);aZ(i)=a3*(G(i,1)-Xs)+b3*(G(i,2)-Ys)+c3*(G(i,3)-Zs);endxj=[];yj=[];for i=1:cxj(i)=-f*aX(i)/aZ(i);yj(i)=-f*aY(i)/aZ(i);enda11=[];a12=[];a13=[];a14=[];a15=[];a16=[];a21=[];a22=[];a23=[];a24=[];a25=[];a26=[];for i=1:ca11(i)=(a1*f+a3*g1(i,1))/aZ(i);a12(i)=(b1_*f+b3*g1(i,1))/aZ(i);a13(i)=(c1*f+c3*g1(i,1) )/aZ(i);a21(i)=(a2*f+a3*g1(i,2))/aZ(i);a22(i)=(b2_*f+b3*g1(i,2))/aZ(i);a23(i)=(c2*f+c3*g1(i,2) )/aZ(i);a14(i)=g1(i,2)*sin(w)-(g1(i,1)*(g1(i,1)*cos(k)-g1(i,2)*sin(k))/f+f*cos(k))*cos(w);a15(i)=-f*sin(k)-g1(i,1)*(g1(i,1)*sin(k)+g1(i,2)*cos(k))/f;a16(i)=g1(i,2);a24(i)=-g1(i,1)*sin(w)-(g1(i,2)*(g1(i,1)*cos(k)-g1(i,2)*sin(k))/f-f*sin(k))*cos(w);a25(i)=-f*cos(k)-g1(i,2)*(g1(i,1)*sin(k)+g1(i,2)*cos(k))/f;a26(i)=-g1(i,1);endlx=[];ly=[];for i=1:clx(i)=g1(i,1)-xj(i);ly(i)=g1(i,2)-yj(i);endA=zeros(2*c,6);for i=1:cA(2*i-1,1)=a11(i);A(2*i-1,2)=a12(i);A(2*i-1,3)=a13(i);A(2*i-1,4)=a14(i);A(2*i-1,5)=a15 (i);A(2*i-1,6)=a16(i); A(2*i,1)=a21(i); A(2*i,2)=a22(i); A(2*i,3)=a23(i); A(2*i,4)=a24(i); A(2*i,5)=a25(i); A(2*i,6)=a26(i);endL=zeros(2*c,1);for i=1:cL(2*i-1,1)=lx(i);endX=inv((A')*A)*(A')*L;Xs=Xs+X(1,1);Ys=Ys+X(2,1);Zs=Zs+X(3,1);q=q+X(4,1);w=w+X(5,1);k=k+X(6,1);Xabs=abs(X);aaa=max(Xabs);if aaa<0.00003 %当改正数中绝对值最⼤的改正数⼩于限差0.00003 break; %后跳出循环，计算结果已经收敛endendglobal V;V=L';global WF QXX;WF(1)=Xs;WF(2)=Ys;WF(3)=Zs;WF(4)=q;WF(5)=w;WF(6)=k;QXX=A'*A;六．实验结果左⽚外⽅位元素Xs,Ys,Zs,ψ、ω、κ、为：5.0001950e+003 5.0007250e+003 2.0201583e+003 -7.2888190e-005 2.8193877e-002 9.5130388e-002左⽚外⽅位元素协因素阵为：4.0166895e-008 -3.7263703e-010 1.3218695e-008 7.0720033e-005 1.0001730e-007 -2.5748604e-006-3.7263703e-010 4.0032797e-008 2.6568407e-009 -2.1103715e-007 7.7772275e-005 1.9993587e-0051.3218695e-0082.6568407e-009 1.7931301e-0083.1008915e-005 6.6697659e-006 5.6403374e-0077.0720033e-005 -2.1103715e-007 3.1008915e-005 1.3087511e-001 1.0148977e-003 -1.9981396e-003 1.0001730e-007 7.7772275e-005 6.6697659e-006 1.0148977e-003 1.5539404e-001 3.0264331e-002-2.5748604e-006 1.9993587e-005 5.6403374e-007 -1.9981396e-003 3.0264331e-002 4.0721943e-002左⽚外⽅位元素Xs,Ys,Zs,ψ、ω、κ、为：5.8967023e+003 5.0687355e+003 2.0506347e+003 1.4337709e-002 4.6257617e-0021.1037952e-001右⽚外⽅位元素协因素阵为：3.9305329e-0084.9400147e-010 -1.0339207e-008 6.8065940e-005 -4.2504770e-007 1.8461496e-0064.9400147e-010 3.9051893e-008 3.3958896e-011 -3.9945442e-008 7.6312421e-005 -1.6453951e-005-1.0339207e-008 3.3958896e-011 1.5155886e-008 -2.3705097e-005 3.5940467e-007 -7.3527082e-007 6.8065940e-005 -3.9945442e-008 -2.3705097e-005 1.2229164e-001 -2.3449223e-003 4.8281474e-003-4.2504770e-007 7.6312421e-005 3.5940467e-007 -2.3449223e-003 1.5233230e-001 -2.5374659e-0022.5374659e-0023.6794789e-002GCP在左⽚和右⽚改正后的坐标（x，y）为：1.6019582e-002 7.9954660e-002 -7.3934212e-002 7.8699356e-0028.8559633e-002 8.1141190e-002 -5.2455612e-003 7.8187184e-0021.3352398e-002 -7.9378247e-002 -7.9125440e-002 -7.8877760e-0028.2242309e-002 -8.0017749e-002 -9.8858970e-003 -8.0086832e-002单位权中误差为：±1.515610577029578e-005所求地⾯点的三维坐标（X, Y, Z）为：5.4310348e+003 5.8851463e+003 5.4831646e+0025.1473645e+003 5.0555934e+003 4.8499600e+0025.4957931e+003 5.0826911e+003 5.0668967e+0025.8442434e+003 5.1098033e+003 5.3025650e+0025.5603279e+003 4.2870779e+003 4.6536459e+002七．⼼得体会经过三周的努⼒，这个当初看来艰巨的任务终于在我的不懈努⼒下圆满的完成了。

中南大学本科生课程设计（实践）任务书、设计报告（摄影测量与遥感概论）题目：空间后方交会-前交院系：地球科学与信息物理学院班级：测绘1201班********学号：***********名：***二零一四年十一月一、实验目的通过对数字影像空间后交前交的程序设计实验，要求我们进一步理解和掌握影像外方位元素的有关理论、原理和方法。

利用计算机程序设计语言编写摄影测量空间交会软件进行快速确定影响的外方位元素及其精度，然后通过求得的外方位元素求解位置点的地面摄影测量坐标，达到通过摄影测量量测地面地理坐标的目的。

二、实验要求1.用C、VB、C++或MA TLAB语言编写空间后方交会-空间前方交会程序2.提交实习报告：程序框图、程序源代码、计算结果、体会3.计算结果：像点坐标、地面坐标、单位权中误差、外方位元素及其精度4.完成时间：11月11日前完成三、实验数据四、实验思路➢利用后方交会得出两张相片各自的外方位元素1）获取已知数据影响比例尺m,，内方位元素x0 、y0 、f ，控制点的地面摄影测量坐标Xtp, Ytp, Ztp2）量测控制点左片和右片的像点坐标 x，y3）确定未知数初值 Xs0, Ys0, Zs0, ω，φ，κ（线元素可用控制点均值代替，角元素可用0初始化），即：∑=Xtp X 41s0，∑=Ytp Y 41s0，f Z *m s =ω=0，φ=0，κ=0 4）计算旋转矩阵R5）利用共线方程逐点计算像点坐标的近似值 6）组成误差方程式并法化 7）解求外方位元素改正数8）检查迭代是否收敛（改正值是否小于某一特定常数） ➢ 利用解出的外方位元素进行前方交会1）获取已知数据x0 , y0 , f, XS1, YS1, ZS1,φ1,ω1,κ1 , XS2, YS2, ZS2，φ2，ω2，κ22）量测像点坐标 x1,y1 ,x2,y23）由外方位线元素计算基线分量BX, BY, BZ4）由外方位角元素计算像空间辅助坐标 X1, Y1, Z1 , X2, Y2, Z2 5）计算点投影系数 N1 , N2 6）计算地面坐标 XA, YA, ZA五、实验过程➢ 程序流程图此过程完成空间后方交会求解像片的外方位元素，其中改正数小于限差（0.00003，相当于0.1的角度值）为止。