下载文档原格式
适合性检验与独立性检验引言在统计学中，适合性检验和独立性检验是非常重要的概念。
适合性检验旨在确定一组观察数据是否与某个特定的概率分布相匹配，而独立性检验旨在确定两个变量之间是否存在相互独立的关系。
适合性检验和独立性检验在不同的统计分析场景中起着重要的作用。
在本文中，我们将介绍适合性检验和独立性检验的基本概念、应用场景以及常用的统计方法。
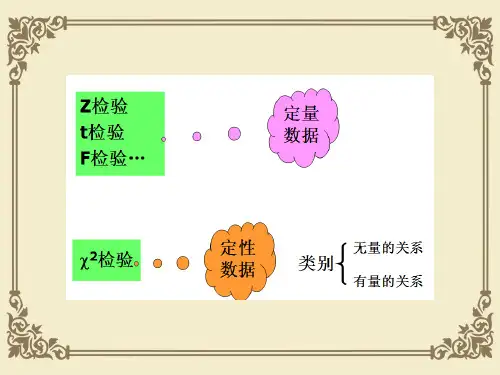
适合性检验适合性检验是用来确定一组观测数据是否与某个特定的概率分布相匹配的方法。
在许多统计分析中，我们常常需要假设观测数据符合某个特定的概率分布，例如正态分布、泊松分布等。
在这种情况下，适合性检验可以帮助我们验证这个假设的合理性。
常见的适合性检验方法有卡方检验和Kolmogorov-Smirnov检验。
卡方检验适用于离散型的观测数据，而Kolmogorov-Smirnov检验适用于连续型的观测数据。
卡方检验卡方检验是一种常见的适合性检验方法。
它基于观察数据与期望数据之间的差异来确定观测数据是否符合某个特定的概率分布。
卡方检验的原假设是观测数据与期望数据完全相符，而备择假设是观测数据与期望数据不完全相符。
卡方检验的计算方法涉及到计算观测频数和期望频数之间的差异，并将差异进行平方、除以期望频数，然后求和。
最后，根据卡方统计量的分布情况，确定观测数据是否与期望数据相匹配。
Kolmogorov-Smirnov检验Kolmogorov-Smirnov检验是另一种常见的适合性检验方法。
它用于检验观测数据是否与某个特定的连续型概率分布相匹配。
Kolmogorov-Smirnov检验基于观测数据的累积分布函数和期望分布函数之间的差异来确定观测数据是否符合某个特定的连续型概率分布。
Kolmogorov-Smirnov检验的原假设是观测数据与期望数据完全相符，而备择假设是观测数据与期望数据不完全相符。
Kolmogorov-Smirnov检验的计算方法涉及到计算观测数据的累积分布函数和期望分布函数之间的差异，并根据差异的最大值来确定观测数据是否与期望数据相匹配。
