(完整word版)平面几何练习题

平面几何练习题 ――点共圆
1. 在直角ABC ∆的两条直角边AC 、BC 上各取一点D 和E ，由顶点C 分别向直线DE 、EA 、AB 、
BD 引垂线，求证，所得的4个垂足共圆；（1989年前苏联教委推荐题）
)
291988(.2候选题届年第共圆；
、、、、、、、、的中点，求证：、、为、、为垂心，为三条高的垂足，、、为三边的中点，、、中，在IMO R Q P Z Y X F E D HC HB HA R Q P H Z Y X F E D ABC ∆
)
191990(.3AMO Q P N M Q P AC AC N M CC AB AB ABC 届年第共圆；
、、、，求证：、于边的高线及其延长线交为直径的圆与以，
、及其延长线交于边的高线为直径的圆与，以给出平面上一个锐角‘
4.凸四边形ABCD 中，两对角线AC 和BD 互相垂直，两对边AB 与CD 不平行，且AB 与CD 的垂直平分线交于四边形内一点P ，证明：ABCD 为圆内接四边形的充要条件是ABP ∆的面积等于CDP ∆的面积。

（1998年第39届IMO ）
)
361995(6,,,,,)()()(.5222111122112211221122112211221候选题届年第个顶点共圆。

求证：这两个三角形的也可构成一个三角形，线可构成一个三角形，直，直线，使得之间与位于、上取两点，在边之间与于位、上取两点，在边之间与位于，，上取两点的边在锐角IMO CC BB AA CC BB AA C CC C CC B BB B BB A AA A AA B C C C C AB A B B B B CA C A A A A BC ABC ∠=∠=∠=∠=∠=∠∆。

（Ⅰ)求证： ；
（Ⅱ)求 与平面 所成角的正弦值；
（Ⅲ）求点 到平面 的距离．
16、如图所示四棱锥 中， 底面 ,四边形 中， ， ， ， ， 为 的中
点， 为 中点。
(1）求四棱锥P－ABCD的体积；（2)求证： 平面 ;
（3)在棱PC上是否存在点M（异于点C），使得BM∥平面PAD，
若存在，求 的值，若不存在 ，说明理由.；
10如图，在直三棱柱 中， , ，且 是 中点.
(I）求证： 平面 ；（Ⅱ）求证： 平面 .
11如图， 在四棱锥P—ABCD中， AB∥CD， AB⊥AD， CD=2AB， 平面PAD⊥底面ABCD， PA⊥AD. E和F分别是CD和PC的中点。 求证:
(Ⅰ） PA⊥底面ABCD;(Ⅱ) BE∥平面PAD；
6。如图,在四棱锥P－ABCD中，底面ABCD为矩形，平面PAB⊥平面ABCD,PA⊥PB， BP＝BC,E为PC的中点．（1)求证：AP∥平面BDE;（2）求证:BE⊥平面PAC．
7如图， 是边长为 的正方形， 平面 ， ， 且 。
（1）求证: ∥平面 ；（2)求证： 平面 平面（3）求几何体ABC NhomakorabeaEF的体积
8。如图，在正三棱锥 中, , 分别为 , 的中点。
(1）求证： 平面 ；（2）求证：平面 平面 .
9。 如图， 直三棱柱ABC—A1B1C1中， D， E分别是AB， BB1的中点.
（Ⅰ) 证明: BC1∥平面A1CD;(Ⅱ) 设AA1=AC=CB=2, AB=2 ， 求三棱锥C—A1DE的体积。
（Ⅰ）求证：AP∥平面BEF；（Ⅱ）求证：BE⊥平面PAC.
3。 如图,四棱锥P—ABCD的底面ABCD是平行四边形,BA=BD= ,AD=2,PA=PD= ,E,F分别是棱AD,PC的中点.

平面几何练习题题一：求三角形边长和周长已知一个三角形的两边长分别为a和b，夹角为C°，求第三边c的长度和三角形的周长P。

解：根据余弦定理可知，余弦公式为：c² = a² + b² - 2ab·cos(C)。

根据上述公式，可以计算得到c的长度。

根据三角形的定义可知，三角形的周长P等于三边之和，即P = a + b + c。

题二：求三角形的面积已知一个三角形的底边长为b，高为h，求三角形的面积S。

解：根据三角形的面积公式可知，S = 0.5 * b * h。

题三：判断点是否在三角形内部已知一个三角形的三个顶点坐标分别为A（x₁，y₁），B（x₂，y₂），C（x₃，y₃），以及一个待判断的点D（x，y），判断点D是否在三角形ABC的内部。

解：利用行列式的性质可以判断点D是否在三角形ABC内部。

设点D的坐标为(x,y)，则点D在三角形ABC内部的条件为：|(x₁ - x) (y₁ - y) 1||(x₂ - x) (y₂ - y) 1| > 0|(x₃ - x) (y₃ - y) 1|如果等式左侧的行列式结果大于0，则点D在三角形ABC内部；如果等式左侧的行列式结果小于0，则点D在三角形ABC的外部；如果等式左侧的行列式结果等于0，则点D在三角形ABC所在的边界上。

题四：求矩形的面积和周长已知一个矩形的长为L，宽为W，求矩形的面积S和周长P。

解：矩形的面积公式为S = L * W，周长公式为P = 2 * (L + W)。

题五：求圆的面积和周长已知一个圆的半径为r，求圆的面积S和周长C（circumference）。

解：圆的面积公式为S = π * r²，其中π取近似值3.14159；圆的周长公式为C = 2 * π * r。

题六：判断点是否在圆内部已知一个圆的圆心坐标为O（x₀，y₀），半径为r，以及一个待判断的点P（x,y），判断点P是否在圆O内部或者在圆的边界上。

平面几何练习题及解答一、直线与角度1. 给定一条直线L1和两条直线L2和L3，若L1与L2垂直，L2与L3平行，则L1与L3之间的夹角为多少度？解答：由于L1与L2垂直，可得出L2的斜率为无穷大，即L2为竖直线。

而L2与L3平行，说明它们具有相同的斜率。

因此，L3的斜率也为无穷大，即L3也是竖直线。

由此可知，L1与L3之间的夹角为90度。

2. 给定一条直线L和两点A、B，若L与AB的垂线相交于点M，且角AMB为40度，则角LMA的度数是多少？解答：由垂线的性质可得出，角LMA与角AMB互补，它们的度数和为90度。

已知角AMB为40度，因此角LMA的度数为90度减去40度，即50度。

二、三角形3. 已知三角形ABC，其中∠B = 90度，AB = 3 cm，BC = 4 cm，求AC的长度。

解答：根据勾股定理可得：AC² = AB² + BC²AC² = 3² + 4²AC² = 9 + 16AC² = 25AC = √25AC = 5 cm4. 已知三角形ABC，其中AB = 6 cm，BC = 8 cm，AC = 10 cm，求∠B的度数。

解答：根据余弦定理可得：BC² = AB² + AC² - 2 * AB * AC * cosB8² = 6² + 10² - 2 * 6 * 10 * cosB64 = 36 + 100 - 120 * cosB64 = 136 - 120 * cosB120 * cosB = 136 - 64120 * cosB = 72cosB = 72 / 120cosB = 0.6根据反余弦函数可得：∠B = arccos(0.6)∠B ≈ 53.13度三、圆的性质5. 在平面直角坐标系中，给定圆心为O(2, 3)，半径为5的圆C，点P(6, 7)是否在圆C上？解答：利用距离公式可计算OP的距离：OP = √((6-2)² + (7-3)²)OP = √((4)² + (4)²)OP = √(16 + 16)OP = √32OP ≈ 5.66由于OP的长度不等于圆C的半径，即5.66不等于5，因此点P不在圆C上。

2024年数学九年级上册平面几何基础练习题（含答案）试题部分一、选择题：1. 在平面几何中，下列哪个图形既是轴对称图形又是中心对称图形？（）A. 矩形B. 等腰三角形C. 梯形D. 正五边形2. 下列各角中，哪个角是补角？（）A. 30°B. 45°C. 60°D. 120°3. 在直角坐标系中，点A(2, 3)关于原点对称的点是（）A. (2, 3)B. (2, 3)C. (2, 3)D. (2, 3)4. 下列哪个条件能判定两个三角形全等？（）A. 两边和其中一边的对角相等B. 两角和其中一边相等C. 两边和它们的夹角相等D. 两边和其中一边的对角相等5. 若平行线l1和l2之间的距离为5cm，直线l3与l1、l2均相交，且l3与l1、l2的夹角均为45°，则l3与l1、l2之间的距离为（）A. 5cmB. 5√2 cmC. 2.5cmD. 2.5√2 cm6. 下列哪个图形是正多边形？（）A. 边长为1，内角为108°的多边形B. 边长为1，内角为120°的多边形C. 边长为1，内角为135°的多边形D. 边长为1，内角为140°的多边形7. 在直角三角形中，若一个锐角的度数为30°，则另一个锐角的度数为（）A. 30°B. 45°C. 60°D. 90°8. 下列哪个比例式成立？（）A. a² : b² = (a+b)² : (ab)²B. a² : b² = (a+b) : (ab)C. a : b = (a+b)² : (ab)²D. a : b = (a+b) : (ab)9. 若等腰三角形的底边长为8cm，腰长为5cm，则该三角形的面积为（）A. 20cm²B. 40cm²C. 30cm²D. 24cm²10. 在平面几何中，下列哪个说法是正确的？（）A. 对角线互相垂直的四边形一定是矩形B. 对角线互相平分的四边形一定是平行四边形C. 对角线相等的四边形一定是矩形D. 对角线互相垂直平分的四边形一定是菱形二、判断题：1. 平行线的性质是：同位角相等，内错角相等，同旁内角互补。

平面几何选讲练习题１．如图所示,已知⊙O 1与⊙O 2相交于A ，B 两点，过点A 作⊙O 1的切线交⊙O 2于点C,过点B 作两圆的割线，分别交⊙O 1，⊙O 2于点D ，E ，DE 与AC 相交于点P 。

（1）求证：AD ∥EC ；(2)若AD 是⊙O 2的切线,且PA=6,PC=2,BD=9，求AD 的长;2．如图：已知AD 为⊙O 的直径，直线BA 与⊙O 相切于点A ，直线OB 与弦AC 垂直并相交于点G ，连接DC 。

求证:BA ·DC =GC ·AD .3． 已知：如图，△ABC 中,AB=AC ，∠BAC=90°，AE=31AC ，BD=31AB ，点F 在BC 上,且CF=31BC.求证: （1)EF ⊥BC ；(2）∠ADE=∠EBC.B E DO 1 O 2A P CF EDABC４．如图，在△ABC 中，D 是AC 的中点,E 是BD 的中点，AE 的延长线交BC 于F .（1)求FCBF 的值;（2）若△BEF 的面积为1S ,四边形CDEF 的面积为2S ，求21:S S 的值．５．已知C 点在圆O 直径BE 的延长线上，CA 切圆O 于A 点，DC 是ACB ∠的平分线交AE 于点F ，交AB 于D 点。

（1)求ADF ∠的度数； （2）若AB=AC ，求AC:BC.６．自圆O 外一点P 引切线与圆切于点A ，M 为PA 中点，过M 引割线交圆于B ，C 两点．求证：∠MCP=∠MPB ． O A BDE F7．如图,AD 是⊙O 的直径，AB 是⊙O 于点M 、N ，直线BMN 交AD 的延长线于点C ，NC MN BM ==，2=AB ，求BC 的长和⊙O 的半径.8．如图，AB 是⊙O 的直径，C ，F 为⊙O 上的点，CA 是∠BAF 的角平分线,过点C 作CD ⊥AF 交AF 的延长线于D 点，CM ⊥AB ，垂足为点M . （1)求证：DC 是⊙O 的切线； (2）求证：AM ·MB =DF ·DA .9．如图，已知AP 是⊙O 的切线,P 为切点，AC 是⊙O 的割线，与⊙O 交于B 、C 两点，圆心O 在PAC ∠的内部，点M 是BC 的中点.（Ⅰ）证明A ，P ,O ,M 四点共圆； (Ⅱ）求∠OAM ＋∠APM 的大小.10．如图 ，过圆O 外一点M 作它的一条切线，切点A ，过A 点作直线AP 垂直直线OM ，垂足为P 。

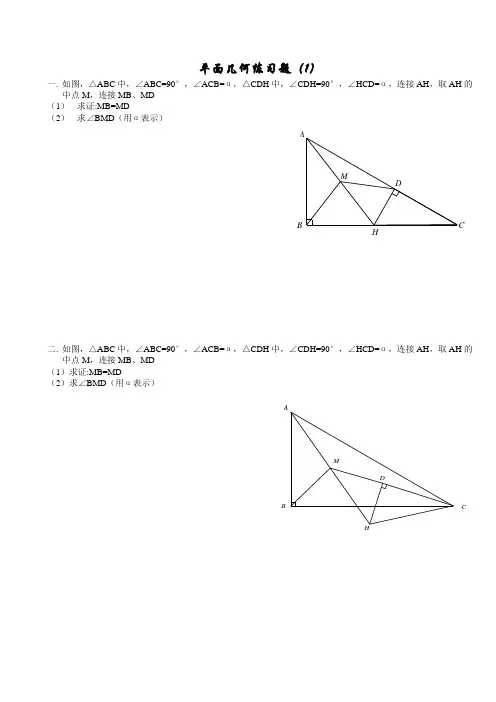
平面几何练习题（1）一.如图，△ABC中，∠ABC=90°，∠ACB=α，△CDH中，∠CDH=90°，∠HCD=α，连接AH，取AH的中点M，连接MB、MD（1）求证:MB=MD（2）求∠BMD（用α表示）MH DCBA二.如图，△ABC中，∠ABC=90°，∠ACB=α，△CDH中，∠CDH=90°，∠HCD=α，连接AH，取AH的中点M，连接MB、MD（1）求证:MB=MD（2）求∠BMD（用α表示）MH DCB A三. 如图，△ABC 中，∠ABC=90°，∠ACB=α，△CDH 中，∠CDH=90°，∠HCD=α，连接AH ，取AH 的中点M ，连接MB 、MD （1）求证:MB=MD（2）求∠BMD （用α表示）ABCDHM四. 如图，△ABC 中，∠ABC=90°，∠ACB=α，△CDH 中，∠CDH=90°，∠HCD=α，连接AH ，取AH 的中点M ，连接MB 、MD （1）求证:MB=MD（2）求∠BMD （用α表示）MHDCBA中点M ，连接MB 、MD （1）求证:MB=MD（2）求∠BMD （用α表示）ABCDHM六. 如图，△ABC 中，∠ABC=90°，∠ACB=α，△CDH 中，∠CDH=90°，∠HCD=α，连接AH ，取AH 的中点M ，连接MB 、MD （1）求证:MB=MD（2）求∠BMD （用α表示）MHDCBAAB CDHM中点M ，连接MB 、MD （1）求证:MB=MD（2）求∠BMD （用α表示）八. 如图，△ABC 中，∠ABC=90°，∠ACB=α，△CDH 中，∠CDH=90°，∠HCD=α，连接AH ，取AH 的中点M ，连接MB 、MD （1）求证:MB=MD（2）求∠BMD （用α表示） MHDCBA。

专题24平面几何的定值问题【阅读与思考】所谓定值问题，是指按照一定条件构成的几何图形，当某些几何元素按一定的规律在确定的范围内变化时，与它有关的元素的量保持不变（或几何元素间的某些几何性质或位置关系不变）.几何定值问题的基本特点是：题设条件中都包含着变动元素和固定元素，变动元素是指可变化运动的元素，固定元素也就是“不变量”，有的是明显的，有的是隐含的，在运动变化中始终没有发生变化的元素，也就是我们要探求的定值.解答定值问题的一般步骤是：1.探求定值；2.给出证明.【例题与求解】—^ PA + PC .【例1】如图，已知P为正方形ABCD的外接圆的劣弧AD上任意一点.求证：一后一为定值.PB解题思路：线段的和差倍分考虑截长补短，利用圆的基本性质，证明三角形全等.【例2】如图，AB为。

O的一固定直径，它把。

O分成上、下两个半圆，自上半圆上一点C作弦CD±AB，Z OCD的平分线交。

O于点P，当点C在上半圆（不包括A，B两点）上移动时，点P（）A.到CD的距离保持不变B.位置不变C.等分DBD.随C点的移动而移动（济南市中考试题）解题思路：添出圆中相关辅助线，运用圆的基本性质，用排除法得出结论.【例3】如图，定长的弦ST在一个以AB为直径的半圆上滑动，M是ST的中点，P是S对AB作垂线的垂足.求证：不管ST滑到什么位置，Z SPM是一定角.（加拿大数学奥林匹克试题）解题思路：不管ST滑到什么位置，Z SOT的度数是定值.从探寻Z SPM与Z SOT的关系入手.【例4】如图，扇形OAB的半径OA=3,圆心角/AOB=90°.点C是箫上异于A, B的动点，过点C作CD±OA于点D,作CE±OB于点E.连接DE,点G, H在线段DE上，且DG=GH=HE.(1)求证：四边形OGCH是平行四边形；(2)当点C在箫上运动时，在CD, CG, DG中，是否存在长度不变的线段？若存在，请求出该线段的长度；(3)求证：CD 2+3 CH2是定值. (广州市中考试题)解题思路：延长OG交CD于N,利用题中的三等分点、平行四边形和三角形中位线的性质，实现把线段ON转化成线段CH的倍分关系，再以及△ OND为基础，通过勾股定理，使问题得以解决.【例5】如图1,在平面直角坐标系xOy中，点M在x轴的正半轴上，。

高中数学练习题：平面几何引子在高中数学中，平面几何是一个重要的知识点，也是学生们经常接触和练习的内容之一。

平面几何涉及到平面上的点、线、面等概念，通过运用几何定律和性质，解决与平面相关的问题。

掌握平面几何的基本概念与方法不仅有助于学生提高逻辑思维和推理能力，还能够拓宽学生的数学视野，使他们能够更好地应用数学知识解决实际问题。

本文将提供一系列高中平面几何的练习题，并逐一解析，帮助读者更好地理解和掌握平面几何的知识。

1. 点、线、面的基本概念H2：点的基本概念练习题 1：在平面上，画出以下图形：•两个不在同一直线上的点•三个共线的点•四个不在同一直线上的点H3：线的基本概念练习题 2：根据以下描述，判断相应的线段关系：•两个线段长度相等的关系是什么？•两个线段互相垂直的关系是什么？•如果一个线段是另一个线段的一半，它们之间的关系是什么？H3：面的基本概念练习题 3：根据以下描述，判断相应的平面关系：•两个平面都垂直于同一条直线的关系是什么？•如果两个平面相交，它们的交线是什么？•两个平行平面之间的夹角是多少？2. 直线与角的性质H2：平行线与相交线练习题 4：判断以下直线关系：•如果两条直线垂直相交，它们之间的夹角是多少？•如果一条直线与另一条直线平行，它们之间的夹角是多少？•如果两条直线相交，它们之间的夹角是多少？H2：三角形与四边形练习题 5：根据以下描述，判断相应的三角形和四边形特征：•如果一个四边形的对角线相等，它是什么形状的四边形？•如果一个三角形的三边相等，它是什么类型的三角形？•一个三角形的两个角相等，它是什么类型的三角形？H3：角的性质练习题 6：根据以下描述，判断相应角的性质：•如果一个角是直角，它的度数是多少？•如果一个角是锐角，它的度数是多少？•如果一个角是钝角，它的度数是多少？H3：三角形的性质练习题 7：根据以下描述，判断相应三角形的性质：•如果一个三角形的三个角都是锐角，它是什么类型的三角形？•如果一个三角形有一个角是钝角，它是什么类型的三角形？•如果一个三角形有一个角是直角，它是什么类型的三角形？3. 圆与圆的性质H2：圆的基本概念练习题 8：根据以下描述，判断相应的圆的性质：•什么是圆心？•什么是半径？•什么是直径？H2：角与圆的性质练习题 9：根据以下描述，判断相应角和圆的性质：•一个角的两条边与圆的切点相接，这个角叫什么？•如果一条边是直径，这个角叫什么？•如果一条边与圆的切点相接，而另一条边不过圆心，这个角叫什么？H3：切线与切点练习题 10：根据以下描述，判断相应的切线和切点的性质：•如果一条直线与圆的切点相接，这条直线叫什么？•如果一条直线与圆的切点相接，并且垂直于半径，这条直线叫什么？•如果一条直线与圆的切点相接，并且平行于半径，这条直线叫什么？4. 平面几何题目解析H2：练习题 11将一张纸对折两次得到四个重叠的小正方形，再按其中一条对角线剪开，得到两个相等的小三角形，请问这两个小三角形相似吗？解析首先，我们知道正方形的对角线可以将正方形分成两个相等的直角三角形。

初二平面几何基础练习题1. 问题描述：在平面上给定一个等边三角形ABC，边长为10cm。

求三角形ABC的高和面积。

解答：设三角形ABC的高为h，由于ABC是等边三角形，所以三角形ABC也是等腰三角形。

连接AB的中点M与C，可得到三角形AMC。

由于AM与CM分别垂直于BC和AB，所以AM和CM就是三角形ABC的高。

根据勾股定理，三角形AMC的斜边AC等于三角形ABC的边长，即AC = 10cm。

由于三角形AMC是直角三角形，所以AM和CM相等，记为AM = CM = h。

根据勾股定理，有AC² = AM² + CM²，即10² = h²+ h² = 2h²。

解方程2h² = 100，可以得到h = √50 ≈ 7.07 cm。

三角形ABC的面积S可以通过底乘高的公式计算，即S = 0.5 × 10× h = 0.5 × 10 × 7.07 ≈ 35.35 cm²。

所以，三角形ABC的高为7.07 cm，面积为35.35 cm²。

2. 问题描述：在平面上给定一个矩形ABCD，已知AB = 12cm，BC = 8cm。

求矩形ABCD的对角线长度和周长。

解答：设矩形ABCD的对角线长度为d。

根据勾股定理，可以得到d² = AB² + BC² = 12² + 8² = 144 + 64 = 208。

解方程d² = 208，可以得到d = √208 ≈ 14.42 cm。

矩形ABCD的周长可以通过将四条边的长度相加得到，即周长 =AB + BC + CD + DA = 12 + 8 + 12 + 8 = 40 cm。

所以，矩形ABCD的对角线长度约为14.42 cm，周长为40 cm。

3. 问题描述：在平面上给定一个圆O，半径为6cm。

平面几何图形面积练习题在平面几何中，图形的面积是一个常见的概念。

计算图形的面积既可以是实际生活中的问题，也可以是学习数学的一个重要知识点。

在本文中，我们将通过一些练习题来巩固对平面几何图形面积计算的理解和应用。

题目一：矩形的面积计算计算下列矩形的面积：1. 长为10厘米，宽为5厘米的矩形的面积是多少？2. 如果一个矩形的长是3倍于宽，且宽为4米，那么它的面积是多少？解答：1. 矩形的面积可以通过长乘以宽来计算。

所以，长为10厘米，宽为5厘米的矩形的面积是10厘米 × 5厘米 = 50平方厘米。

2. 根据题目中的条件，该矩形的长为3 × 4米 = 12米。

因此，它的面积为12米 × 4米 = 48平方米。

题目二：三角形的面积计算计算下列三角形的面积：1. 底边长为10厘米，高为6厘米的三角形的面积是多少？2. 边长分别为5厘米、12厘米和13厘米的三角形的面积是多少？解答：1. 三角形的面积可以通过底边乘以高再除以2来计算。

所以，底边长为10厘米，高为6厘米的三角形的面积是（10厘米 × 6厘米）/ 2 = 30平方厘米。

2. 根据海伦公式，我们可以通过三角形的边长来计算其面积。

设三角形的三边长分别为a、b、c，它们的半周长为s，那么三角形的面积可以通过以下公式计算：面积= √(s × (s - a) × (s - b) × (s - c))，其中，s = (a + b + c) / 2。

根据题目中给出的边长，可以计算得到s = (5厘米 + 12厘米 + 13厘米) / 2 = 15厘米。

代入公式计算得到面积= √(15厘米 × (15厘米 - 5厘米) × (15厘米 - 12厘米) × (15厘米 - 13厘米)) = 30平方厘米。

题目三：圆的面积计算计算下列圆的面积：1. 半径为5厘米的圆的面积是多少？2. 直径为8厘米的圆的面积是多少？解答：1. 圆的面积可以通过半径的平方乘以π（即3.14159...）来计算。

平面图形上的最短路径问题知识点：1.两点之间，线段最短2.垂线段最短3.线段垂直平分线是的点到线段两端点的距离相等4.三角形任意两边之差小于第三边总思路：找点关于线的对称点实现“折”转“直”常考题型题：将军饮马、造桥选址、费马点（一）根据两点之间，线段最短题型一两点在直线同侧（将军饮马）题型二相交直线之间一点或两点题型四费马点（二）根据垂线段最短题型五和最小（三）根据线段垂直平分线上点到线段两端点距离相等题型六差最小（四）根据三角形任意两边之差小于第三边题型七差最大题型一两点在直线同侧例题1：如图，在锐角△ABC中，AB=6，∠BAC=60°，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是（）A．3B．6解：在AC上取一点E，使得AE=AB，过E作EN⊥AB于N′，交AD于M，连接BM，BE，BE交AD于O，则BM+MN’最小（根据两点之间线段最短；点到直线垂直距离最短），∵AD平分∠CAB，AE=AB，∴EO=OB，AD⊥BE，∴AD是BE的垂直平分线（三线合一），∴E和B关于直线AD对称，∴EM=BM，即BM+MN′=EM+MN′=EN′，∵EN’⊥AB，∴∠EN’A=90°，∵∠CAB=60°，∴∠AEN′=30°，∵AE=AB=6，∴AN’=3，在△AEN’中，由勾股定理得：EN’即BM+MN B．巩固练习：如图，在平面直角坐标系中，R t△OAB的顶点A在x轴的正半轴上．顶点B的坐标为（3，点C的坐标为（1，0），且∠AOB=30°点P为斜边OB上的一个动点，则P A+PC的最小值为____ _____．解：作A关于OB的对称点D，连接CD交OB于P，连接AP，过D作DN⊥OA于N，则此时P A+PC的值最小．∵DP=P A，∴P A+PC=PD+PC=CD．∵B（3，∴AB OA=3，∠B=60°．由勾股定理得：OB OA×AB OB×AM，∴AM AD．∵∠AMB=90°，∠B=60°，∴∠BAM=30°．∵∠BAO=90°，∴∠OAM=60°．∵DN⊥OA，∴∠NDA=30°．∴AN由勾股定理得：DN C（1，0），∴CN=3-1在R t△DNC中，由勾股定理得：DC∴P A+PC题型二相交直线之间一或两点例题2：如图，∠AOB=30°，∠AOB内有一定点P，且OP=10．在OA上有一点Q，OB上有一点R ．若△PQR 周长最小，则最小周长是（ ）A ．10B ．15C ．20D ．30 解：设∠POA =θ，则∠POB =30°﹣θ，作PM ⊥OA 与OA 相交于M ，并将PM 延长一倍到E ，即ME =PM ． 作PN ⊥OB 与OB 相交于N ，并将PN 延长一倍到F ，即NF =PN ． 连接EF 与OA 相交于Q ，与OB 相交于R ，再连接PQ ，PR ， 则△PQR 即为周长最短的三角形．∵OA 是PE 的垂直平分线， ∴EQ =QP ；同理，OB 是PF 的垂直平分线， ∴FR =RP ， ∴△PQR 的周长=EF ． ∵OE =OF =OP =10，且∠EOF =∠EOP +∠POF =2θ+2（30°﹣θ）=60°， ∴△EOF 是正三角形，∴EF =10，即在保持OP =10的条件下△PQR 的最小周长为10，故选A ．巩固练习：如图，∠AOB =30°，点M 、N 分别在边OA 、OB 上，且OM =5，ON =12，点P 、Q 分别在边OB 、OA 上，则MP +PQ +QN 的最小值是 ．解：作M 关于OB 的对称点M ′，作N 关于OA 的对称点N ′，连接M’N’，即为MP +PQ +QN 的最小值．根据轴对称的定义可知：∠N ′OQ =∠M ′OB =30°，∠ONN ′=60°，OM’=OM =5，ON’=ON =12， ∴△ONN ′为等边三角形，△OMM ′为等边三角形， ∴∠N′OM′=90°，∴在Rt M ON ''中，''13M N = 故答案为：13．题型三 造桥选址例题3：荆州护城河在CC＇处直角转弯，河宽相等，从A处到达B处，需经过两座桥DD＇、EE＇，护城河及两桥都是东西、南北方向，桥与河岸垂直．如何确定两座桥的位置，可使A 到B点路径最短？解：作AF⊥CD，且AF=河宽，作B G⊥CE，且BG=河宽，连接GF，与河岸相交于E’、D’，作DD’、EE’即为桥证明：由做法可知，AF∥DD’，AF=DD’，则四边形AFDD’为平行四边形于是AD=FD’同理，BE=G E’由两点之间线段最短可知，GF最小即当桥建于如图所示位置时，ADD’E’EB最短巩固练习：如图，工厂A和工厂B被一条河隔开，它们到河的距离都是2km，两个工厂水平距离是3km，河宽1km，现在要架一座垂直于河岸的桥，使工厂A到工厂B的距离最短（河岸是平行的）①请画出架桥的位置（不写画法）②求从工厂A经过桥到工厂B的最短路程.解：①如图所示，AA’=1km，则MN为架桥位置A B===②过点B作BE⊥AA’，交其延长线于点E。

平面几何练习题（一）1、在△ABC的边AC上取点D，E，使得AD=AB，BE=EC，（E在A与D之间），点F是△ABC外接圆上（不含A点的）BC弧的中点，求证：B、E、D、F四点共圆.FA2、在△ABC中，BC>AB，BD平分∠ABC 交AC于D，如图，CP垂直于BD，垂足为P，AQ垂直于BP，垂足为Q，M是AC的中点，E是BC的中点.若△PQM的外接圆O与AC的另一个交点为H.求证：O，H，E，M四点共圆.C3、AB是圆O的直径，C为AB延长线上一点，过点C作圆O的割线，与圆O交于D，E两点，OF是△BOD的外接圆O1的直径，连接CF并延长交圆O1 于点G .求证：O、A、E、G四点共圆.A4、如图，在锐角△ABC中，AB<AC，AD是边BC上的高，P是线段AD内一点。

过P作PE⊥AC，垂足为E，做PF⊥AB，垂足为F。

O1、O2分别是△BDF、△CDE的外心。

求证：O1、O2、E、F四点共圆的充要条件为P是△ABC的垂心。

B平面几何练习一参考答案1、证明：设∠ABC=α.因AB=AD ，故∠ABD=α,∠BAD=180°-2α.∠CBF 的度数等于21CF 弧的度数，而∠CAB 的度数等于21BC 弧的度数，所以∠CBF=21∠CAB =90°-α，点E ，F 分别与点B ，C 等距，所以EF 垂直平分BC.因此∠BFE=90°-∠CBF=90°-（90°-α）=α.于是∠BDE=∠BFE=α，所以B 、F 、D 、E 四点共圆.2、证明：如图联结PH ，作AQ 延长线交BC 于N ，则Q 为AN 的中点. M 为AC中点，∴QM ∥BC.故∠PQM=∠PBC=1/2∠ABC,同理，延长CP 交BA 延长线于N '可得P M ∥B N '，因此∠MPQ =∠ABP=1/2∠ABC ，∴QM=PM.又 Q,H,P,M 四点共圆， ∴∠PHC =∠PHM=∠PQM ，得∠PHC =∠PBC ，∴P,H,B,C 四点共圆，得∠BHC =∠BPC =90°，故HE=1/2BC=EP.结合OH=OP ，知OE 为HP 的中垂线，由∠MPQ =1/2∠ABC=∠PBC 及E 为BC 的中点可得P,M,E 共线，故∠EHO =∠EPO=∠OPM=∠OMP ，所以 O,H,E,M 四点共圆.3、证明：联结AD,DG,GA,GO,EA,EO.因为OFOF 平分∠DOB ，又因为∠DAB=1/2∠DOB ，所以∠DAB=∠DOF ，又∠DGF=∠DOF ，所以∠DAB=∠DGF ，所以G ,A,C,D 四点共圆，所以∠AGC=∠AD C ①，而∠AGC= ∠AGO +∠OGF=∠AGO+π/2，② ∠ADC=∠ADB +∠BDC=∠BDC+π/2，③结合①②③得∠AGO=∠BD C .因为B,D,E,A 四点共圆，所以∠BDC=∠EAO ，又OA=OE ，有∠AEO=∠EAO ，所以∠AGO=∠AEO ，故O,A,E,G 四点共圆.AC。

平面几何练习题及答案一、选择题1. 已知三角形ABC中，∠A=90°，AB=3cm，BC=4cm，求AC的长度。

A. 5cmB. 6cmC. 7cmD. √7cm2. 在矩形PQRS中，若PS=6cm，QR=8cm，求对角线PR的长度。

A. 10cmB. 12cmC. 14cmD. √(6²+8²)cm3. 圆O的半径为5cm，点A在圆上，点B在圆外，且OA=5cm，OB=10cm，求AB的长度。

A. 5cmB. 10cmC. 15cmD. √(10²-5²)cm二、填空题4. 已知等腰三角形的底边长为6cm，两腰长为5cm，求其面积。

答案：____cm²5. 已知直角三角形的两条直角边分别为3cm和4cm，求其外接圆的半径。

答案：____cm6. 已知正六边形的边长为a，求其内切圆的半径。

答案：____三、计算题7. 在三角形DEF中，DE=7cm，DF=8cm，EF=9cm，求三角形DEF的面积。

8. 已知圆的半径为r，圆心为O，点A在圆上，点B在圆外，OA=r，OB=2r，求AB的长度。

9. 已知矩形LMNP的长为10cm，宽为6cm，求其内切圆的半径。

四、证明题10. 证明：在直角三角形中，斜边的中线等于斜边的一半。

11. 证明：如果一个三角形的两边和其中一边上的高相等，那么这个三角形是等腰三角形。

12. 证明：在等边三角形中，每个内角都是60°。

五、解答题13. 已知圆的半径为r，求圆的周长和面积。

14. 已知矩形ABCD的长为a，宽为b，求对角线AC的长度。

15. 已知三角形ABC的三个顶点坐标分别为A(x1, y1)，B(x2, y2)，C(x3, y3)，求三角形ABC的面积。

答案：1. D2. D3. D4. 12cm²5. 2.5cm6. a/√37. 27cm²8. 5r9. 2cm10. 利用直角三角形斜边上的中线等于斜边的一半的性质证明。

(时间：40分钟)1．直线2x ＋y ＋m ＝0和x ＋2y ＋n ＝0的位置关系是( ) A ．平行 B ．垂直C ．相交但不垂直D ．不能确定 答案 C解析 由⎩⎪⎨⎪⎧2x ＋y ＋m ＝0，x ＋2y ＋n ＝0，可得3x ＋2m －n ＝0，由于3x ＋2m －n ＝0有唯一解，故方程组有唯一解，故两直线相交，两直线的斜率分别为－2，－12，斜率之积不等于－1，故不垂直，故选C.2．已知直线l 1：x ＋ay ＋6＝0和l 2：(a －2)x ＋3y ＋2a ＝0平行，则实数a 的值为( ) A ．3 B ．－1 C ．1 D ．－1或3 答案 B解析 由l 1∥l 2，得－1a ＝－a －23，解得a ＝3或a ＝－1，验证当a ＝3时，l 1，l 2的方程分别为x ＋3y ＋6＝0，x ＋3y ＋6＝0，l 1与l 2重合．∴a ＝－1，故选B.3．直线l 1：kx ＋(1－k )y －3＝0和l 2：(k －1)x ＋(2k ＋3)y －2＝0相互垂直，则k ＝( ) A ．－3或－1 B ．3或1 C ．－3或1 D ．－1或3 答案 C解析 若1－k ＝0，即k ＝1，直线l 1：x ＝3，l 2：y ＝25，明显两直线垂直．若k ≠1，直线l 1，l 2的斜率分别为k 1＝kk －1，k 2＝1－k 2k ＋3.由k 1k 2＝－1，得k ＝－3.综上k ＝1或k ＝－3，故选C. 4．不论m 为何值时，直线(m －1)x ＋(2m －1)y ＝m －5恒过定点( ) A.⎝⎛⎭⎪⎫1，－12 B ．(－2,0)C ．(2,3)D ．(9，－4) 答案 D解析 由(m －1)x ＋(2m －1)y ＝m －5，得(x ＋2y －1)·m －(x ＋y －5)＝0，由⎩⎪⎨⎪⎧x ＋2y －1＝0，x ＋y －5＝0，得定点坐标为(9，－4)，故选D.5．已知两点A (3,2)和B (－1,4)到直线mx ＋y ＋3＝0的距离相等，则m 的值为( )A ．0或－12 B.12或－6C ．－12或12D ．0或12答案 B解析 依题意，得|3m ＋5|m 2＋1＝|－m ＋7|m 2＋1.化简得8m 2＋44m －24＝0，所以2m 2＋11m －6＝0.所以m ＝12或m ＝－6，故选B.6．两条平行直线l 1：3x ＋4y －4＝0与l 2：ax ＋8y ＋2＝0之间的距离是________．答案 1解析 由直线l 1：3x ＋4y －4＝0与l 2：ax ＋8y ＋2＝0平行，可得a ＝6，l 2的方程为3x ＋4y ＋1＝0，两直线间的距离d ＝|c 1－c 2|A 2＋B 2＝|－4－1|32＋42＝1. 7．点P (2,1)到直线l ：mx －y －3＝0(m ∈R )的最大距离是________． 答案 2 5解析 直线l 经过定点Q (0，－3)，如图所示．由图知，当PQ ⊥l 时，点P (2,1)到直线l 的距离取得最大值|PQ |＝2－02＋1＋32＝25，所以点P (2,1)到直线l 的最大距离为2 5.8．已知点P (x ，y )到A (0,4)和B (－2,0)的距离相等，则2x＋4y的最小值为________． 答案 4 2解析 由题意得，点P 在线段AB 的中垂线上，则易得x ＋2y ＝3，∴2x＋4y≥22x·4y＝22x ＋2y＝42，当且仅当x ＝2y ＝32时等号成立，故2x ＋4y的最小值为4 2.9．已知两条直线l 1：ax －by ＋4＝0和l 2：(a －1)x ＋y ＋b ＝0，求满足下列条件的a ，b 的值：(1)l 1⊥l 2，且l 1过点(－3，－1)；(2)l 1∥l 2，且坐标原点到这两条直线的距离相等． 解 (1)由已知可得l 2的斜率存在，且k 2＝1－a . 若k 2＝0，则1－a ＝0，a ＝1.∵l 1⊥l 2，∴直线l 1的斜率k 1必不存在，即b ＝0. 又∵l 1过点(－3，－1)， ∴－3a ＋4＝0，即a ＝43(冲突)，∴此种状况不存在，∴k 2≠0，即k 1，k 2都存在．∵k 2＝1－a ，k 1＝a b，l 1⊥l 2， ∴k 1k 2＝－1，即ab(1－a )＝－1.①又∵l 1过点(－3，－1)，∴－3a ＋b ＋4＝0.② 由①②联立，解得a ＝2，b ＝2.(2)∵l 2的斜率存在，l 1∥l 2，∴直线l 1的斜率存在，k 1＝k 2，即ab＝1－a .③又∵坐标原点到这两条直线的距离相等，且l 1∥l 2， ∴l 1，l 2在y 轴上的截距互为相反数，即4b＝b ，④联立③④，解得⎩⎪⎨⎪⎧a ＝2，b ＝－2或⎩⎪⎨⎪⎧a ＝23，b ＝2.∴a ＝2，b ＝－2或a ＝23，b ＝2.10．已知直线l ：2x －3y ＋1＝0，点A (－1，－2)．求： (1)点A 关于直线l 的对称点A ′的坐标；(2)直线m ：3x －2y －6＝0关于直线l 的对称直线m ′的方程； (3)直线l 关于点A (－1，－2)对称的直线l ′的方程． 解 (1)设A ′(x ，y )，由已知条件得⎩⎪⎨⎪⎧y ＋2x ＋1×23＝－1，2×x －12－3×y －22＋1＝0，解得⎩⎪⎨⎪⎧x ＝－3313，y ＝413.∴A ′⎝ ⎛⎭⎪⎫－3313，413. (2)在直线m 上取一点，如M (2,0)，则M (2,0)关于直线l 的对称点M ′必在直线m ′上． 设对称点M ′(a ，b )，则⎩⎪⎨⎪⎧2×a ＋22－3×b ＋02＋1＝0，b －0a －2×23＝－1，得M ′⎝ ⎛⎭⎪⎫613，3013.设直线m 与直线l 的交点为N ，则由⎩⎪⎨⎪⎧2x －3y ＋1＝0，3x －2y －6＝0，得N (4,3)．又∵m ′经过点N (4,3)，∴由两点式得直线m ′的方程为9x －46y ＋102＝0. (3)解法一：在l ：2x －3y ＋1＝0上任取两点，如M (1,1)，N (4,3)，则M ，N 关于点A (－1，－2)的对称点M ′，N ′均在直线l ′上， 易得M ′(－3，－5)，N ′(－6，－7)， 再由两点式可得l ′的方程为2x －3y －9＝0. 解法二：∵l ∥l ′，∴设l ′的方程为2x －3y ＋C ＝0(C ≠1)． ∵点A (－1，－2)到两直线l ，l ′的距离相等， ∴由点到直线的距离公式，得|－2＋6＋C |22＋32＝|－2＋6＋1|22＋32，解得C ＝－9， ∴l ′的方程为2x －3y －9＝0.解法三：设P (x ，y )为l ′上任意一点， 则P (x ，y )关于点A (－1，－2)的对称点为P ′(－2－x ，－4－y )．∵点P ′在直线l 上，∴2(－2－x )－3(－4－y )＋1＝0， 即2x －3y －9＝0. (时间：20分钟)11．已知直线l 的倾斜角为34π，直线l 1经过点A (3,2)，B (a ，－1)，且l 1与l 垂直，直线l 2：2x ＋by＋1＝0与直线l 1平行，则a ＋b 等于( )A ．－4B ．－2C ．0D ．2 答案 B解析 由题意知l 的斜率为－1，则l 1的斜率为1， ∴k AB ＝2－－13－a＝1，解得a ＝0.由l 1∥l 2，得－2b＝1，b ＝－2，所以a ＋b ＝－2，故选B.12．若P ，Q 分别为直线3x ＋4y －12＝0与6x ＋8y ＋5＝0上任意一点，则|PQ |的最小值为( ) A.95 B.185 C.2910 D.295 答案 C解析 由于36＝48≠－125，所以两直线平行，由题意可知|PQ |的最小值为这两条平行直线间的距离，即|－24－5|62＋82＝2910，所以|PQ | 的最小值为2910. 13．已知入射光线经过点M (－3,4)，被直线l ：x －y ＋3＝0反射，反射光线经过点N (2,6)，则反射光线所在直线的方程为________________．答案 6x －y －6＝0解析 设点M (－3,4)关于直线l ：x －y ＋3＝0的对称点为M ′(a ，b )，则反射光线所在直线过点M ′，所以⎩⎪⎨⎪⎧b －4a －－3·1＝－1，－3＋a 2－b ＋42＋3＝0，解得a ＝1，b ＝0.又反射光线经过点N (2,6)，所以所求直线的方程为y －06－0＝x －12－1，即6x －y －6＝0.14．已知直线l ：x －2y ＋8＝0和两点A (2,0)，B (－2，－4)． (1)在直线l 上求一点P ，使|PA |＋|PB |最小； (2)在直线l 上求一点P ，使||PB |－|PA ||最大．解 (1)设A 关于直线l 的对称点为A ′(m ，n )，则⎩⎪⎨⎪⎧n －0m －2＝－2，m ＋22－2·n ＋02＋8＝0，解得⎩⎪⎨⎪⎧m ＝－2，n ＝8，故A ′(－2,8)．P 为直线l 上的一点，则|PA |＋|PB |＝|PA ′|＋|PB |≥|A ′B |，当且仅当B ，P ，A ′三点共线时，|PA |＋|PB |取得最小值，为|A ′B |，点P 即是直线A ′B 与直线l 的交点，解⎩⎪⎨⎪⎧x ＝－2，x －2y ＋8＝0，得⎩⎪⎨⎪⎧x ＝－2，y ＝3，故所求的点P 的坐标为(－2，3)．(2)A ，B 两点在直线l 的同侧，P 是直线l 上的一点，则||PB |－|PA ||≤|AB |，当且仅当A ，B ，P 三点共线时，||PB |－|PA ||取得最大值，为|AB |，点P 即是直线AB 与直线l 的交点，又直线AB 的方程为y ＝x －2，解⎩⎪⎨⎪⎧y ＝x －2，x －2y ＋8＝0，得⎩⎪⎨⎪⎧x ＝12，y ＝10，故所求的点P 的坐标为(12,10)．。

课时规范练41直线与圆、圆与圆的位置关系基础巩固组1.(2021浙江余姚中学月考)直线mx-y+1=0与圆(x-2)2+(y-1)2=5的位置关系是()A.相交B.相切C.相离D.与m的值有关2.(2021湖南长沙一中月考)已知圆x2+y2=25,则过圆上一点A(3,4)的切线方程为()A.3x+4y-25=0B.4x+3y-24=0C.3x-4y+7=0D.4x-3y=03.(2021河南安阳一中月考)若直线l:mx+ny+3=0始终平分圆C:x2-2x+y2+3y-1=0,则2m-3n=()A.-6B.-3C.3D.64.(2021安徽合肥一中模拟)“k∈[-2,√3]”是“直线l:y=kx与圆C:(x-2)2+y2=3相交”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件5.(多选)已知圆C1:x2+y2-10x-10y=0和圆C2:x2+y2-6x+2y-40=0,则()A.两圆相交B.公共弦长为4√10C.两圆相离D.公共弦长为2√106.(多选)(2021湖南怀化一模)直线l过点P(1,2)且与直线x+ay-3=0平行.若直线l被圆x2+y2=4截得的弦长为2√3,则实数a的值可以是()A.0B.34C.43D.-437.两圆x2+y2-4x+2y+1=0与(x+2)2+(y-2)2=9的公切线有条.8.(2021河北秦皇岛二模)已知直线x+y-5=0与圆C:(x-2)2+(y-1)2=4相交于A,B两点,则△ABC的面积为.9.(2021湖北荆州模拟)已知圆C过点A(4,-1),且与直线x-y+1=0相切于点B(-2,-1).(1)求圆C的方程;(2)设直线y=x与圆C相交于M,N两点,求弦长|MN|.综合提升组10.(多选)(2021河北张家口二模)已知直线l:kx+y=0与圆M:x2+y2-2x-2y+1=0,则下列说法中正确的是()A.直线l与圆M一定相交B.若k=0,则直线l与圆M相切C.当k=-1时,直线l被圆M截得的弦最长D.圆心M到直线l的距离的最大值为√211.(多选)(2021山东淄博三模)已知圆O1:x2+y2-2x-3=0和圆O2:x2+y2-2y-1=0的交点为A,B,则()A.圆O1和圆O2有两条公切线B.直线AB的方程为x-y+1=0C.圆O2上存在两点P和Q使得|PQ|>|AB|D.圆O1上的点到直线AB的最大距离为2+√212.(2021山东烟台二中三模)已知直线ax+y-2=0与圆C:x2+y2-2x-2ay+a2-3=0相交于A,B两点,且△ABC为钝角三角形,则实数a的取值范围为.13.若一个圆的圆心是抛物线x2=8y的焦点,且该圆与直线√3x-y-2=0相切,则该圆的标准方程为.过点P(-2,-2)作该圆的两条切线PA,PB,切点分别为A,B,则直线AB的方程为.创新应用组14.(2021北京高三一模)瑞士著名数学家欧拉在1765年证明了定理:三角形的外心、重心、垂心位于同一条直线上,这条直线被后人称为三角形的“欧拉线”.在平面直角坐标系中作△ABC,AB=AC=4,B(-1,3),C(4,-2),且其“欧拉线”与圆M:(x-a)2+(y-a+3)2=r2相切.则圆M上的点到直线x-y+3=0的距离的最小值为() A.2√2 B.3√2C.4√2D.615.阿波罗尼斯与阿基米德、欧几里得被称为亚历山大时期数学三巨匠.“阿波罗尼斯圆”是他的代表成果之一;平面上一点P到两定点A,B的距离满足|PA||PB|=t(t>0且t≠1)为常数,则点P的轨迹为圆.已知圆O:x2+y2=1和点A(-12,0),若定点B(b,0)(b≠-12)和常数λ满足:对圆O上任意一点M,都有|MB|=λ|MA|,则λ=,△MAB面积的最大值为.课时规范练41 直线与圆、圆与圆的位置关系1.A 解析因为直线mx-y+1=0过定点(0,1),且(0-2)2+(1-1)2=4<5, 所以点(0,1)在圆内,所以直线和圆相交.故选A .2.A 解析因为圆x 2+y 2=25的圆心为O (0,0),所以直线AO 的斜率k OA =43,所以切线的斜率k=-1k OA =-34,所以切线方程为y-4=-34(x-3),化简得3x+4y-25=0.故选A .3.A 解析由圆C :x 2-2x+y 2+3y-1=0得圆心C (1,-32).因为直线平分圆,所以直线必过圆心(1,-32),则m-32n+3=0,则2m-3n=-6.故选A . 4.B 解析由直线与圆相交,得圆心到直线的距离为d=√k +1<√3,解得k ∈(-√3,√3).因为(-√3,√3)⫋[-2,√3],所以[-2,√3]是直线l 与圆C 相交的必要不充分条件. 故选B .5.AB 解析圆C 1的标准方程为(x-5)2+(y-5)2=50,圆心为(5,5),半径为r 1=5√2. 圆C 2的标准方程为(x-3)2+(y+1)2=50,圆心为(3,-1),半径为r 2=5√2. ∵圆心距d=√(5-3)2+[5-(-1)]2=2√10,∴|r 1-r 2|<d<r 1+r 2,∴两圆相交,故选项A 正确,选项C 错误; 设两圆公共弦长为L ,则有(L 2)2+(d 2)2=r 2(r=r 1=r 2),∴L=4√10,故选项B 正确,选项D 错误. 故选AB .6.AD 解析设直线l 的方程为x+ay+c=0(c ≠-3). 因为直线l 过点P (1,2),所以c=-1-2a , 所以直线l 的方程为x+ay-2a-1=0. 圆x 2+y 2=4的圆心为(0,0),半径为2.因为直线l 被圆x 2+y 2=4截得的弦长为2√3,所以弦心距为1, 所以圆心到直线的距离d=√a 2+1=1,解得a=0或a=-43.故选AD .7.3 解析圆x 2+y 2-4x+2y+1=0整理可得(x-2)2+(y+1)2=4,可得圆心C 1的坐标为(2,-1),半径r 1=2.(x+2)2+(y-2)2=9的圆心C 2的坐标为(-2,2),半径r 2=3,所以圆心距|C 1C 2|=√(2+2)2+(2+1)2=5=r 1+r 2,所以两个圆外切,所以公切线有3条.8.2解析因为圆C:(x-2)2+(y-1)2=4的圆心为C(2,1),半径r=2,所以圆心C到直线x+y-5=0的距离d=√2=√2,所以直线x+y-5=0被圆C:(x-2)2+(y-1)2=4截得的弦长|AB|=2√4-2=2√2,所以△ABC面积S=12×2√2×√2=2.9.解(1)过切点B(-2,-1)且与直线x-y+1=0垂直的直线为y+1=-(x+2),即x+y+3=0,则其过圆心.∵直线AB方程为y=-1,∴AB的中垂线x=1过圆心.联立{x+y+3=0,x=1,解得{x=1,y=-4,∴圆心为(1,-4),∴半径r=√(1+2)2+(-4+1)2=3√2,∴所求圆的方程为(x-1)2+(y+4)2=18.(2)∵直线l的方程为x-y=0,∴圆心C(1,-4)到直线l的距离d=√2,∴|MN|=2√18-d2=√22.10.BCD解析M:x2+y2-2x-2y+1=0,即(x-1)2+(y-1)2=1,是以点(1,1)为圆心,以1为半径的圆.对于A,因为直线l:kx+y=0过原点,且02+02-2×(-2)×0+1>0,所以原点在圆外,所以直线l 与圆M不一定相交,故A错误;对于B,若k=0,则直线l:y=0,直线l与圆M相切,故B正确;对于C,当k=-1时,直线l的方程为y=x,过圆M的圆心,故C正确;对于D,由点到直线的距离公式,得d=√k+1=√k2+1+2kk2+1=√1+2k+1k≤√2(当且仅当k=1时,等号成立),故D正确.故选BCD.11.ABD解析对于A,因为两个圆相交,所以有两条公切线,故A正确;对于B,将两圆方程相减可得-2x+2y-2=0,即得直线AB的方程为x-y+1=0,故B正确;对于C,直线AB过圆O2的圆心(0,1),所以线段AB是圆O2的直径,所以圆O2中不存在比AB长的弦,故C错误;对于D,圆O1的圆心坐标为(1,0),半径为2,圆心到直线AB:x-y+1=0的距离为√2=√2,所以圆O1上的点到直线AB的最大距离为2+√2,故D正确.故选ABD.12.(2-√3,1)∪(1,2+√3)解析圆C:x2+y2-2x-2ay+a2-3=0可化为(x-1)2+(y-a)2=4,故圆心为C(1,a),半径为2.当△ABC为等腰直角三角形时,点C到直线的距离d=√a2+1=√2,解得a=2±√3.∵△ABC为钝角三角形,∴0<d<√2.又当a=1时,d=0,∴a的取值范围为(2-√3,1)∪(1,2+√3).13.x2+(y-2)2=4x+2y-2=0解析由题意,圆心坐标为F(0,2).因为该圆与直线√3x-y-2=0相切,所以d=|-2-2|2=2=r,所以圆的标准方程为x2+(y-2)2=4.因为∠FAP=∠FBP=π2,所以点F,A,B,P四点共圆,且FP为该圆的直径,所以圆的方程为(x+1)2+y2=5.又因为x2+(y-2)2=4,联立求解得x+2y-2=0,所以直线AB的方程为x+2y-2=0.14.A解析因为在△ABC中,AB=AC=4,所以BC边上的高、垂直平分线和中线合一,则其“欧拉线”为△ABC边BC的垂直平分线AD.因为B(-1,3),C(4,-2),所以D(32,12).因为直线BC的斜率为3+2-1-4=-1,所以边BC的垂直平分线的斜率为1,所以边BC的垂直平分线方程为y-12=x-32,即x-y-1=0.因为△ABC的“欧拉线”与圆M:(x-a)2+(y-a+3)2=r2相切,所以圆心M(a,a-3)到“欧拉线”的距离为√2=r,解得r=√2.因为圆心(a,a-3)到直线x-y+3=0的距离为√2=3√2,所以圆M上的点到直线x-y+3=0的距离的最小值为3√2−√2=2√2.故选A.15.234解析设点M(x,y).由|MB|=λ|MA|(λ≥0),得(x-b)2+y2=λ2x+122+y2,整理得(-λ2)x2+(1-λ2)y2-(2b+λ2)x+b2-14λ2=0.因为b=-12,所以|MB|≠|MA|,所以λ≠1,所以1-λ2≠0,所以x2+y2-2b+λ21-λ2x+b2-14λ21-λ2=0,所以{2b+λ21-λ2=0,b2-14λ21-λ2=-1,解得{λ=1,b=-12(舍去)或{λ=2,b=-2.如图所示,S△MAB=12|AB||y M|.由图可知,当|y M|=1,即M的坐标为(0,1)或(0,-1)时,S△MAB取得最大值12-12-(-2)=34.。

探索平面几何的旋转角度计算练习题在平面几何中，旋转角度的计算是一种常见的题型，需要通过几何知识和运算方法来解答。

本文将通过一系列旋转角度计算练习题，帮助读者更好地探索和理解平面几何中旋转的概念和计算方法。

题目一：已知点A(-2, 3)绕原点逆时针旋转45°，求旋转后点的坐标。

解析：根据平面几何的旋转规律，在直角坐标系中，逆时针旋转一个点45°，可以利用以下公式计算旋转后的坐标：\[\begin{align*}x' & = x \cdot \cos{\theta} - y \cdot \sin{\theta} \\y' & = x \cdot \sin{\theta} + y \cdot \cos{\theta}\end{align*}\]其中，x和y是旋转前点的坐标，x'和y'是旋转后点的坐标，θ是旋转角度。

将题目中给出的点A的坐标代入公式，计算可得：\[\begin{align*}x' & = -2 \cdot \cos{45°} - 3 \cdot \sin{45°} \\& = -2 \cdot \frac{\sqrt{2}}{2} - 3 \cdot \frac{\sqrt{2}}{2} \\& = -\sqrt{2} - \frac{3\sqrt{2}}{2} \\& = -\frac{5\sqrt{2}}{2}\end{align*}\]\[\begin{align*}y' & = -2 \cdot \sin{45°} + 3 \cdot \cos{45°} \\& = -2 \cdot \frac{\sqrt{2}}{2} + 3 \cdot \frac{\sqrt{2}}{2} \\& = -\sqrt{2} + \frac{3\sqrt{2}}{2} \\& = \frac{\sqrt{2}}{2}\end{align*}\]所以，点A(-2, 3)绕原点逆时针旋转45°后的坐标为(-\frac{5\sqrt{2}}{2}, \frac{\sqrt{2}}{2})。