2.5 矩阵的秩及其求法

矩阵求秩方法
求矩阵的秩是线性代数中常见的问题，以下是关于矩阵求秩的10条方法及其详细描述：
1. 奇异值分解法：通过对矩阵进行奇异值分解，将矩阵变换为一个对角矩阵，其中非零元素的个数即为矩阵的秩。

2. 初等变换法：利用矩阵的初等行（列）变换，将矩阵化简为行简化阶梯型矩阵，其中非零行的个数即为矩阵的秩。

3. 极大线性无关组法：通过逐步选择矩阵中的列，构建一个极大线性无关组，其中向量的个数即为矩阵的秩。

4. 秩-零空间法：矩阵的秩与其零空间的维数之和为矩阵的列数。

可以通过计算矩阵的零空间 (null space) 的维数来求解矩阵的秩。

5. 行列式法：矩阵的行列式非零的最大子阵的阶数就是矩阵的秩。

6. 直接检验法：将矩阵转换为梯形矩阵或行阶梯矩阵，其中非零行的个数即为矩阵的秩。

7. 特征值法：矩阵的秩等于其特征值不为零的个数。

8. 与单位矩阵求秩法：通过将矩阵与单位矩阵进行连接，得到一个增广矩阵，进而将其化简为行简化阶梯型矩阵，其中非零行的个数即为矩阵的秩。

9. Gauss-Jordan消元法：通过高斯消元法和高斯约当消元法将矩阵化简为行简化阶梯型矩阵，其中非零行的个数即为矩阵的秩。

10. 极大线性无关组与生成组比较法：利用极大线性无关组与生成组的关系来求解矩阵的秩，其中生成组的个数等于矩阵的秩。

矩阵秩的定义以及求法好的，以下是为您创作的关于“矩阵秩的定义以及求法”的科普文章：---当我们听到“矩阵秩”这个词时，可能会觉得它像个神秘的密码，让人摸不着头脑。

但别担心，让我们一起来揭开它神秘的面纱。

想象一下，你正在参加一场盛大的派对。

派对上的人们站成了一排排、一列列，形成了各种各样的队形。

这些队形就像是矩阵，而矩阵的秩，就好比是这个队形的“稳固程度”或者说“独特程度”。

比如说，大家站成了一排整齐的直线，这是一种比较简单、平凡的队形。

但如果大家一会儿组成一个三角形，一会儿又组成一个复杂的多边形，那这种队形就显得更加独特和有“内涵”。

在矩阵中，秩就是用来衡量这种“独特性”和“复杂程度”的指标。

那么，从数学的角度来说，矩阵的秩到底是什么呢？简单来讲，矩阵的秩就是矩阵中线性无关的行向量或者列向量的最大个数。

有点抽象？没关系，我们来举个例子。

假设有一个矩阵：\[\begin{pmatrix}1 &2 &3 \\2 & 4 & 6 \\3 & 6 & 9\end{pmatrix}\]我们可以通过一系列的操作来求它的秩。

首先，我们发现第二行是第一行的 2 倍，第三行是第一行的 3 倍。

这就意味着第二行和第三行都可以由第一行通过线性组合得到。

所以，真正“独立”、“有个性”的行向量只有第一行。

因此，这个矩阵的秩就是 1。

那怎么求矩阵的秩呢？通常有两种常见的方法，一种是通过初等行变换把矩阵化为行阶梯形，另一种是利用矩阵的行列式。

初等行变换就像是给矩阵做“整形手术”，把它变得更加“标准”和“好看”，直到我们能一眼看出它的秩。

而行列式呢，如果一个矩阵的行列式不为零，那么它的秩就等于它的行数（或者列数）。

矩阵的秩在现实生活中有很多神奇的应用。

比如说在通信领域，信号的传输和处理就常常涉及到矩阵的秩。

想象一下手机信号在空间中传播，这些信号可以用矩阵来表示，而矩阵的秩就能帮助工程师们判断信号的稳定性和有效性，从而优化通信质量，让我们的通话更加清晰，网络更加流畅。

求矩阵的秩的例题讲解
矩阵的秩的定义
矩阵的子式：从矩阵中任意选取n行，再任意选取n列，这n 行n列的公共部分所组成的行列式就是该矩阵的一个n阶子式。

例题：
理解了矩阵的子式，现在来一起学习“矩阵的秩的定义”
矩阵的秩：
如果某矩阵
1. 至少有一个a阶子式不为0
2. 所有大于a阶的所有子式都等于0
则称该矩阵的秩为a。

PART02矩阵的秩的求法
特殊情况：奇数步遇0
解决办法：若正下方有非0的数，则换行；若正下方没有非0的数，则关注点右移
例题：
解答：
PART03矩阵的秩的公式。

求矩阵的秩的三种方法矩阵是线性代数中的一个重要概念，它由一个数域中的矩形阵列组成，是线性变换的一种表现形式。

矩阵的秩是矩阵的重要性质之一，它可以告诉我们矩阵中行向量或列向量之间的关系。

在实际应用中，求解矩阵的秩是非常常见的问题。

本文将介绍矩阵的三种求解秩的方法。

方法一：高斯消元法高斯消元法是求解矩阵秩的一种基础方法。

对于一个矩阵A，如果它的秩为r，则A必然存在一个大小为r的非零行列式。

我们可以通过对矩阵A进行初等行变换将矩阵转化为行简化阶梯矩阵，然后统计矩阵中非零行的个数来确定矩阵的秩。

具体步骤如下：1. 对矩阵A进行高斯列变换，将A转化为行简化阶梯矩阵形式。

2. 统计矩阵中非零行的个数，即为矩阵的秩。

对于下面的矩阵A，我们可以通过高斯消元法求解矩阵的秩：$$A=\begin{bmatrix}1 &2 & 3\\4 &5 & 6\\7 & 8 & 9\end{bmatrix}$$按照高斯消元法的步骤对A进行初等行变换，得到行简化阶梯矩阵：方法二：矩阵的列空间对于一个矩阵A，其列空间是由A中所有列向量所张成的向量空间。

矩阵的秩等于它的列空间的维度。

我们可以先求解矩阵A的列空间的维度，然后确定矩阵A的秩。

具体步骤如下：2. 取矩阵A中与非零列对应的列向量，将它们作为张成列空间的一组基。

3. 求解列空间的维度，即为矩阵A的秩。

阶梯矩阵中非零列的位置分别是1和2，因此取A中的第1列和第2列作为列空间的一组基。

可以看出，这组基中存在一个线性关系：第2列 = 2*第1列。

矩阵A的列空间实际上只由A中的第1列张成，其维度为1，因此矩阵A的秩为1。

总结：本文介绍了求解矩阵秩的三种方法：高斯消元法、矩阵的列空间和矩阵的行空间。

对于一般的矩阵，三种方法的求解结果并不一定相同。

但无论采用哪种方法，都能够有效地求解矩阵的秩。

还有一些特殊的矩阵，它们的秩具有一些特殊性质：1. 对于一个n阶矩阵A，如果它是一个可逆矩阵，那么它的秩为n。

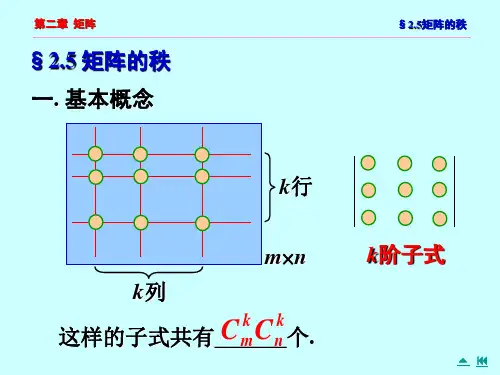
第五节：矩阵的秩及其求法一、矩阵秩的概念1. ｋ 阶子式定义1 设 在A 中任取k 行ｋ 列交叉处元素按原相对位置组成的 阶行列式,称为A 的一个k 阶子式。

例如 共有 个二阶子式，有 个三阶子式 矩阵A 的第一、三行,第二、四列相交处的元素所构成的二阶子式为 而 为 A 的一个三阶子式。

显然, 矩阵 A 共有 个 k 阶子式。

２. 矩阵的秩定义2 设 有r 阶子式不为0，任何ｒ+1阶子式(如果存在的话)全为0 , 称ｒ为矩阵Ａ的秩,记作R (Ａ）或秩(A )。

规定： 零矩阵的秩为 0 .注意：(1) 如 R ( A ) = r ，则 A 中至少有一个 r 阶子式 所有 r + 1 阶子式为 0,且更高阶子式均为 0,r 是 A 中不为零的子式的最高阶数，是唯一的 .（2) 有行列式的性质, （3) R(Ａ) ≤m , R (A ) ≤n ， ０ ≤R (A ） ≤min { m , n } ．(4) 如果 An ×ｎ , 且 则 R( A ） = n .反之，如 R ( Ａ ) = n ,则因此,方阵 Ａ 可逆的充分必要条件是 R ( A ) = n ．二、矩阵秩的求法1、子式判别法（定义)。

例1 设 为阶梯形矩阵,求Ｒ（B ）。

解 由于 存在一个二阶子式不为0,而任何三阶子式全为0,则 Ｒ(B ) = 2.结论：阶梯形矩阵的秩=台阶数。

例如()n m ij a A ⨯={}),m in 1(n m k k ≤≤⎪⎪⎪⎭⎫ ⎝⎛----=110145641321A 182423=C C 43334=C C 10122--=D 1015643213-=D n m ⨯k n k m c c ()n m ij a A ⨯=0,r D ≠()().T R A R A =0,A ≠0.A ≠⎪⎪⎪⎭⎫ ⎝⎛=000007204321B 02021≠⎪⎪⎪⎭⎫ ⎝⎛=010*********A ⎪⎪⎪⎭⎫ ⎝⎛=001021B ⎪⎪⎪⎭⎫ ⎝⎛=100010011C 125034000D ⎛⎫ ⎪= ⎪ ⎪⎝⎭21235081530007200000E ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭()3=A R ()2=B R ()3=C R ()2R D =()3R E =一般地，行阶梯形矩阵的秩等于其“台阶数”—— 非零行的行数。

矩阵的秩及求法矩阵是线性代数中重要的概念，它有许多重要的性质和应用。

其中，矩阵的秩可以用来描述一个矩阵的性质，是矩阵理论中的重要概念之一。

本文将介绍矩阵的秩及求法。

1. 矩阵的秩矩阵的秩是描述矩阵线性无关的最大列数或行数，可以用来判断矩阵的特征和性质。

矩阵的秩可以分为列秩和行秩，两者是相等的。

当矩阵的行秩或列秩为r时，称该矩阵的秩为r，用rank(A)表示。

矩阵的秩可以看作是矩阵中某个部分的线性独立数量，它可以影响到方程组的解的数目，同时也可以影响到矩阵的行列式的值，因此矩阵的秩是矩阵理论中非常重要的一个概念。

求矩阵的秩是矩阵理论中常见的问题之一，有许多的求法。

下面我们将介绍几种常用的求法。

2.1 高斯消元法高斯消元法是求解矩阵秩的一种常用方法。

具体操作步骤如下：1）将矩阵A转化为行阶梯形矩阵U。

2）计算矩阵U中非零行的数量，这个数量就是矩阵A的秩。

例如，对于如下的矩阵：$$\left[ \begin{matrix}1&2&1\\2&2&-1\\-1&-1&2\end{matrix} \right]$$非零行的数量为3，因此该矩阵的秩为3。

2.2 奇异矩阵判定法奇异矩阵是指矩阵的行列式为0的矩阵。

如果一个矩阵是奇异矩阵，则其秩为小于矩阵的维数。

因此，我们可以通过判断矩阵的行列式是否为0来快速判定矩阵是否是奇异矩阵。

其行列式可以计算得到：$det(A)=-1$，因此该矩阵不是奇异矩阵，秩为3。

2.3 矩阵的基变换法我们可以进行列基变换，将其转化为：3. 总结矩阵的秩是描述矩阵线性无关的最大列数或行数。

我们可以通过高斯消元法、奇异矩阵判定法、矩阵的基变换法等方法来求解矩阵的秩。

在实际问题中，矩阵的秩有着重要的应用价值，例如矩阵的逆矩阵等。

求矩阵的秩的方法矩阵的秩啊，这可真是个有趣的东西！就好像是一座神秘城堡的钥匙，能打开很多奇妙的大门呢！要找到矩阵的秩，我们可以用行变换或者列变换呀。

这就像是给矩阵来一场华丽的变身，把它变得更加清晰明了。

比如说，我们可以通过不断地变换矩阵的行，让那些隐藏的规律和关系都浮现出来。

这就好比在黑暗中点亮一盏明灯，一下子就能看清周围的情况啦。

或者呢，我们也可以从列的角度去思考，把列进行巧妙的调整，就像给一幅画重新上色，让它呈现出不一样的精彩。

有时候啊，遇到一些复杂的矩阵，就像是遇到了一团乱麻，但别着急呀，只要耐心地去梳理，总能找到头绪的。

你想想看，一个庞大的矩阵，里面蕴含着多少信息呀！而我们要做的就是从这些信息中找到最关键的那部分，也就是矩阵的秩。

这可不是一件容易的事儿呢，但也正因为有挑战，才更有意思呀！就好像攀登一座高峰，虽然过程艰辛，但当你站在山顶俯瞰一切的时候，那种成就感简直无与伦比。

我们可以通过观察矩阵的行与行之间、列与列之间的关系，去发现那些隐藏的线索。

这就好像是侦探在破案，要从蛛丝马迹中找到真相。

而且哦，不同的矩阵可能需要不同的方法和技巧去求解它的秩。

这就像是每个人都有自己独特的性格，我们要因材施教呀。

有时候，可能一下子就找到了答案；有时候，可能要经过反复的尝试和探索。

但这又有什么关系呢？每一次的尝试都是一次成长，每一次的探索都是一次进步。

在求解矩阵的秩的过程中，我们也能锻炼自己的思维能力和逻辑推理能力。

这可不仅仅是数学上的收获，更是对我们自身能力的提升呀。

总之，求矩阵的秩是一个充满乐趣和挑战的过程，它就像一个神秘的宝藏等待着我们去发掘。

只要我们保持热情和耐心，就一定能找到属于我们自己的宝藏！。

求矩阵的秩的三种方法
计算矩阵的秩有三种常用的方法，分别是高斯消元法、矩阵的行列式和矩阵的特征值。

1. 高斯消元法：
- 将矩阵转换为行简化阶梯形矩阵。

- 统计非零行的个数即为矩阵的秩。

2. 矩阵的行列式：
- 计算原始矩阵的行列式。

- 将其中各个子阵的行列式相乘，并记下非零元素的数量。

- 非零元素的数量即为矩阵的秩。

3. 矩阵的特征值：
- 计算矩阵的特征值。

- 非零特征值的个数即为矩阵的秩。

这三种方法在计算矩阵的秩时都能够得到相同的结果。

矩阵的秩8个公式及证明
矩阵的秩是线性代数中的一个重要概念，它描述了矩阵中线性无关的列（或行）的最大数量。

下面我将列举并证明矩阵的秩的八个公式。

1. 零矩阵的秩为0，证明很简单，因为零矩阵中没有非零的行或列。

2. 对角矩阵的秩等于非零对角元素的个数，证明也比较简单，因为对角矩阵中只有对角线上的元素可能非零，所以秩等于非零对角元素的个数。

3. 初等变换不改变矩阵的秩，初等变换包括交换矩阵的两行（列），用非零常数乘以矩阵的某一行（列），以及用一个非零常数乘以矩阵的某一行（列）加到另一行（列）上。

这些操作不改变矩阵的秩。

4. 行（列）等价的矩阵具有相同的秩，行等价指的是通过一系列的初等行变换可以相互转化的矩阵，列等价类似。

由于初等变换不改变矩阵的秩，所以行（列）等价的矩阵具有相同的秩。

5. 矩阵的秩不超过它的行数和列数中的较小值，这是因为矩阵
的秩描述的是矩阵中线性无关的列（或行）的最大数量，而这个数
量不可能超过矩阵的行数或列数。

6. 对于任意的矩阵A和B，秩(A + B) ≤ 秩(A) + 秩(B)，证
明过程比较复杂，可以使用矩阵的行列式性质和秩的定义进行证明。

7. 对于任意的矩阵A和B，秩(AB) ≤ min(秩(A), 秩(B))，
证明过程比较复杂，可以使用矩阵的行列式性质和秩的定义进行证明。

8. 对于任意的矩阵A，秩(A) = 秩(A^T)，这个公式的证明比
较简单，可以通过矩阵的转置操作和秩的定义进行证明。

综上所述，这是矩阵的秩的八个公式及其证明。

这些公式在线
性代数中具有重要的应用和意义。

秩的计算方法
秩的计算方法指的是在矩阵或向量中，确定其线性无关组或线性相关性质时所采用的一种运算方法。

对于矩阵而言，秩的定义是该矩阵的行(列)向量组的线性无关向量个数，用r(A)表示。

秩可以通过高斯消元法求解，将矩阵转化为行最简形式后，非零行的个数即为矩阵的秩。

对于向量而言，秩的定义是该向量组的线性无关向量个数，用r(V)表示。

求解方式与矩阵类似，将向量组构成矩阵后，通过高斯消元法求取矩阵的秩。

在实际应用中，秩的计算方法应用广泛，如矩阵求逆、矩阵分解、线性方程组求解等。

- 1 -。