aX1+ X2+X3=4 当a、b取何值时 X1+ bX2+X3=3 有唯一解?无解? X1+2bX2+X3=4 有无穷解?
解: 对增广矩阵作初等行变换化为阶梯型矩阵。
a1 1 4 A= 1 b 1 3
1 2b 1 4
1b 1 3 0 1 1-a 4-2a 0 0 ab-b 2ab-4b+1
A: 1 b 1 3 0 1 1-a 4-2a 0 0 ab-b 2ab-4b+1
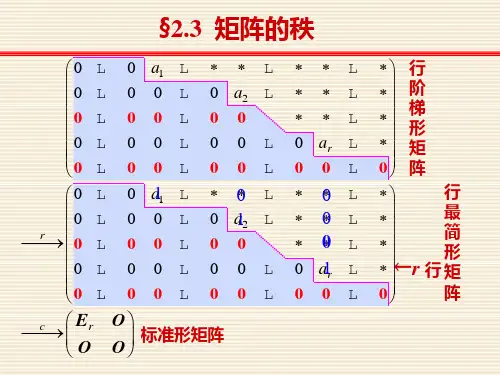
3、向量组线性相关性的判断
• 由向量组A:a1,a2,...,am构成的矩阵A=(a1,a2,...,am) ① 向量组A线性相关的充要条件是R(A)<m; ② 线性无关的充要条件是R(A)=m。
例2:
设α1=(1,0,5,2),α2=(3,-2,3,-4),α3=(-1,1,t,3)线性相 关,求参数t。
α,α2,α3线性相关。
秩相关的公式:
• (1)转置后秩不变 • (2)r(A)<min(m,n),A是m*n型矩阵 • (3)r(kA)=r(A),k不等于0 • (4)r(A)=0 -> A=0 • (5)r(A+B)<=r(A)+r(B) • (6)r(A*B)<=min(r(A),r(B)) • (7)r(A)+r(B)-n<=r(A*B) • 特别的:A:m*n,B:n*s,A*B=0 -> r(A)+r(B)<=n • (8)P,Q满秩方阵(秩等于维数)->r(PA)=r(A)=r(AQ)=r(PAQ)
系数矩阵B: a 1 1 1 b1 1 2b 1
1.当ab-b≠0时,即a≠1且b≠0时,R(A)=R(B)=3,方程 组有唯一解。 2.当a=1,b=1/2时,R(A)=R(B)=2<3,方程组有无穷多解。 3.其他情况,也即当a=1,b≠1/2时,或b=0时, R(A)≠R(B),方程组无解。