下载文档原格式
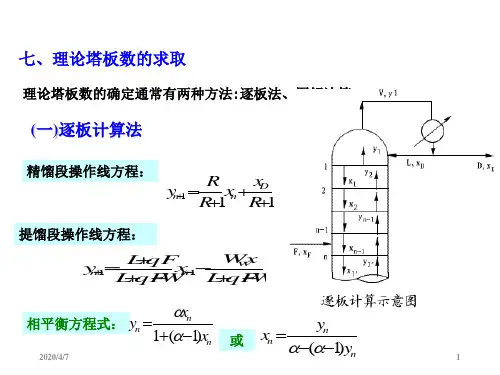
第五节 理论板数的求法所谓求理论塔板数，就是利用前面讨论的平衡关系，()n n x f y =和操作关系，()()m n n x f y x f y ''='=+或1计算达到指定分离要求所须的汽化-冷凝次数。
（1）逐板计算法每利用一次平衡关系和一次操作关系，即为一块理论板。
提馏段也是一样。
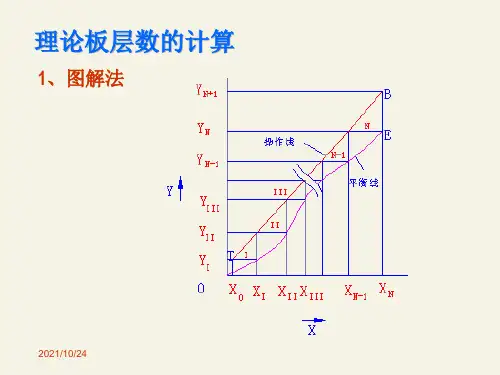
（2）图解法通常采用直角梯级图解法，其实质仍然是以平衡关系与操作关系为依据，将两者绘在y x -图上，便可图解得出达到指定分离任务所须的理论塔板数及加料板位置。
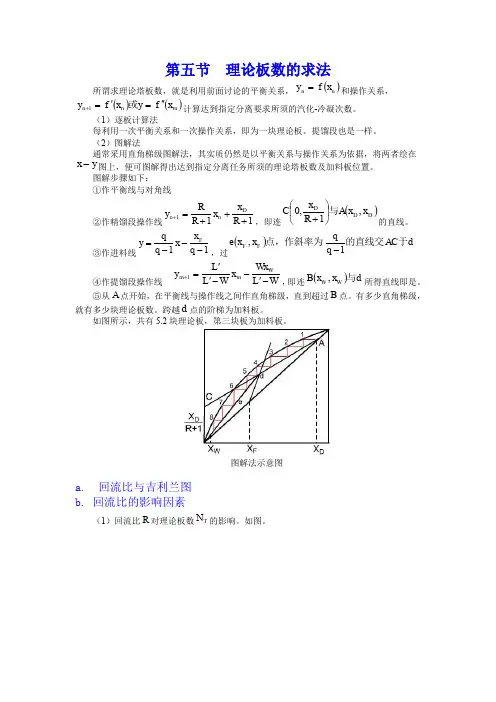
图解步骤如下： ①作平衡线与对角线②作精馏段操作线111+++=+R x x R R y D n n ，即连()D D D x x A R x C ,1,0与⎪⎭⎫ ⎝⎛+的直线。
③作进料线11---=q x x q qy F，过()d AC q q x x e F F 于的直线交点，作斜率为1,- ④作提馏段操作线W L Wx x W L L y W m m -'--''=+1，即连()d x x B W W 与,所得直线即是。
⑤从A 点开始，在平衡线与操作线之间作直角梯级，直到超过B 点。
有多少直角梯级，就有多少块理论板数。
跨越d 点的阶梯为加料板。
如图所示，共有5.2块理论板，第三块板为加料板。
图解法示意图a. 回流比与吉利兰图b. 回流比的影响因素（1）回流比R 对理论板数T N 的影响。
如图。
回流比对T N 的影响↑+↓1R x R D ，，操作线靠近平衡线，↑T N 反之，↓+↑1R x R D ，，操作线远离平衡线，↓T N 即 T N 正比于R 1（2）回流比对设备费与操作费的影响 ()D R D L V 1+=+=↑↑V R ,，塔直径↑，冷凝器↑，蒸馏釜↑ 设备费↑↓↑T N R ,，塔高下降，设备费↓↑↑V R ,，冷却水量↑，加热蒸汽量↑， 操作费↑须选一个合适回流比R ，使总费用最省。
实验数据：
（1）全回流 R=∞
乙醇、正丙醇的相对挥发度α为1.56，R=∞
∴相平衡方程：y=1.56x/（1+0.56x），操作线方程为y=x
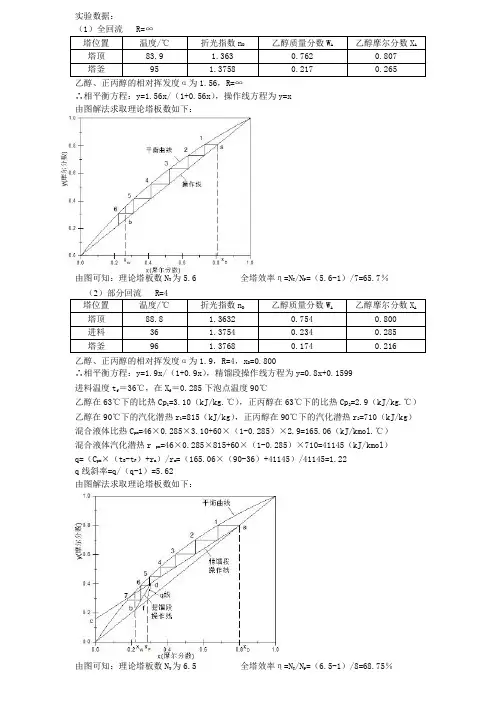
由图解法求取理论塔板数如下：
由图可知：理论塔板数N T为5.6 全塔效率η=N T/N P=（5.6-1）/7=65.7％
乙醇、正丙醇的相对挥发度α为1.9，R=4，x D=0.800
∴相平衡方程：y=1.9x/（1+0.9x），精馏段操作线方程为y=0.8x+0.1599
进料温度t f＝36℃，在X f＝0.285下泡点温度90℃
乙醇在63℃下的比热Cp1=3.10（kJ/kg.℃），正丙醇在63℃下的比热Cp2=2.9（kJ/kg.℃）乙醇在90℃下的汽化潜热r1=815（kJ/kg），正丙醇在90℃下的汽化潜热r2=710（kJ/kg）混合液体比热C pm=46×0.285×3.10+60×（1-0.285）×2.9=165.06（kJ/kmol.℃）
混合液体汽化潜热r pm=46×0.285×815+60×（1-0.285）×710=41145（kJ/kmol）
q=（C pm×（t B-t F）+r m）/r m=（165.06×（90-36）+41145）/41145=1.22
q线斜率=q/（q-1）=5.62
由图解法求取理论塔板数如下：
由图可知：理论塔板数N T为6.5 全塔效率η=N T/N P=（6.5-1）/8=68.75％。
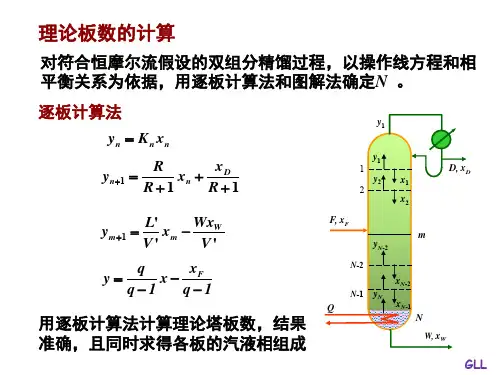
一、图解法求理论板数
图解法计算精馏塔的理论板数和逐板计算法一样，也是利用汽液平衡关系和操作关系，只是把气液平衡关系和操作线方
程式描绘在y x -相图上，使繁琐数学运算
简化为图解过程。
两者并无本质区别，只是
形式不同而己。
（1）精馏段操作线的作法 由精馏段
操作线方程式可知精馏段操作线为直线，只
要在x y -图上找到该线上的两点，就可标
绘出来。
若略去精馏段操作线方程中变量的
下标， 1
1+++=R x x R R y D 上式中截距为
1+R x D ，在图7－12中以c 点表示。
当D x x =时，代入上式得
D x y =，即在对角线上以a 点表示。
a 点代
表了全凝器的状态。
联ac 即为精馏段操作线。
（2）提馏段操作线的作法 由q 线ef ，即可求得它和精馏段操作线的交点，而q 线是两操作线交点的轨迹，故这一交点必然也是两操作线的交点d,联接bd 即得提馏段操作线。
（3）图解法求理论板数的步骤
①在直角坐标纸上绘出待分离的双组分混合物在操作压强下的y x -平衡曲线，并作出对角线。
如图7-14所示。
②依照前面介绍的方法作精馏段的操作线ac ，q 线ef ，提馏段操作线bd 。
③从a 点开始，在精馏段操作线与平衡线之间作水平线及垂直线构成直角梯级，当梯级跨过d 点时，则改在提馏段与平衡线之间作直角梯级，直至梯级的水平线达到或跨过b 点为止。
④梯级数目减一即为所需理论板数。
每一个直角梯级代表一块理论板，这结合逐板计算法分析不难理解。
其中过d 点的梯级为加料板，最后一级为再沸器。
因再沸器相当于一块理论板，故所需理论板数应减一。
在图7-14中梯级总数为７。
第四层跨过d 点，即第４层为加料板，精馏段共3层，在提馏段中，除去再沸器相当的一块理论板，则提馏段的理论板数为4-1=3。
该分离过程共需6块理论板（不包括再沸器）。
图解法较为简单，且直观形象，有利于对问题的了解和分析，目前在双组分连续精馏计算中仍广为采用。
但对于相对挥发度较小而所需理论塔板数较多的物
系，结果准确性较差。
二、适宜的进料位置
在设计中确定适宜进料板位置的问题也就是如何选择加料位置可使总理论板数最少。
适宜的进料位置一般应在塔内液相或汽相组成与进料组成相近或相同的塔板上。
当采用图解法计算理论板时，适宜的进料位置应为跨过两操作线交点所对应的阶梯。
对于一定的分离任务，选此位置所需理论板数为最少，跨过两操作线交点后继续在精馏段操作线与平衡线之间作阶梯，或没有跨过交点就更换操作线，都会使所需理论板数增加。
对于已有的精馏装置，在适宜进料位置进料，可获得最佳分离效果。
在实际操作中，进料位置过高，会使馏出液的组成偏低（难挥发组分偏高）；反之，使釜残液中易挥发组分含量增高，从而降低馏出液中易挥发组分的收率。
对于实际的塔，往往难以预先准确确定最佳进料位置，特别是当料液浓度和其他操作条件有变化时，因此通常在相邻的几层塔板上均装有进料管，以便调整操作时选用。
