回路分析法
- 格式:docx
- 大小:49.56 KB
- 文档页数:5




网孔(回路)电流法分析方法总结摘要网孔电流法在现代电路分析中是一种极为基础且重要的分析方法,所以学习网孔电流法对学习电路有着极其重要的意义。
本文介绍了网孔电流法的一般分析方法和基本原理,给出了含有受控源和无伴电流源源的处理方法,并结合一部分实例,指出了网孔电流法的具体解法。
关键词网孔电流法、回路电流法、应用实例。
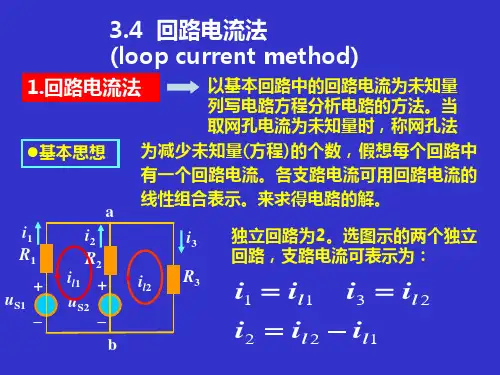
正文一、网孔电流法的原理1、适用条件:在网孔电流法中,以网孔电流作为电流的独立变量,仅适用于平面电路。
2、推理过程:以图1的电路图说明。
图如下:在R1与R2、R3之间的结点(设为结点①)处用结点电流法,有:-i1+i2+i3=0。
可见i2不是独立的,它由另外两个量决定。
我们将图中所有电流归结为由两个网孔连续流动的假象电流,将它们分别称之为i m1和i m2.根据网孔电流和支路电流的参考方向的给定,可以得出其间的关系i1= i m1,i3= i m2,i2= i m1- i m2。
由于网孔电流已经体现了KCL制约方程。
所以用网孔电流作为电路变量求解时只需列出KVL方程。
由于每一个网孔是一个独立的回路,因而可以列出两个KVL方程,对应的有两个未知量i m1和i m2均可求出。
这是网孔电流法。
对上图所示电路,先确定网孔电流的绕行方向,再逐段写出电阻及电源上的电压。
列出KVL。
对于网孔1:R2(i m1-i m2)+V2-V1+R1i m1=0对于网孔2:R3i m2+V3-V2+R2(i m1-i m2)=0对上述2式整理可得:(R1+ R2)i m1- R2i m2= V1-V2-R2i m1+ (R2+R3)i m2= V2-V3可认为上式是对网孔电流为求解对象的网孔电流方程。
现用R11和R22分别代表网孔1和网孔2的自阻,即分别为网孔1和网孔2所有电阻之和;用R12和R21表示网孔1和网孔2的互阻,即两个网孔共用的电阻,此例中有R12=R21= -R2。
上式可写为:R11i m1+R12i m2= V1-V2R21i m1+R22i m2= V2-V3此形式即为网孔电流法的方程。


解:设三个回路电流分别为、、则:1m I 2m I 3m I 图1图2MATLAB 把矩阵指令和结果如下:];[02U I m 解:设三个回路电流分别为、、,则:1m I 2m I 3m I 图3图4u I m 5.03-= 补充方程为: iI I m m =-31 i I I m m 5.012=- u I I m m =-32 由此可以解出、、、、。
A I m 11=A I m 32=A I m 33-=A i 4=A u 6= 将方程整理为: 14000)11(0321=+++-++U u i I I I m m m 000)11(00321=-++-++U u i I I I m m m 005.00000321=+++++U u i I I I m m m 00000321=++--+U u i I I I m m m 0005.000321=++-++-U u i I I I m m m 00000321=+-+-+U u i I I I m m m 然后用MATLAB 计算如下:其中];;;;;[321o m m m U u i I I I x =a=[1+1 0 -1 0 0 1;0 1+1 -1 0 0 -1;0 0 1 0 0.5 0;1 0 -1 -1 0 0;-1 10 -0.5 0 0;0 1 -1 0 -1 0];%定义a 矩阵b=[14;0;0;0;0;0];x=a\b %定义b 矩阵并求解运行结果为:x = 1 3 -3 4 6 9在以上例题中,采用的思想是找准未知量,采用分离变量的方法让未知量在方程组的一侧,然后把方程组写成矩阵形式Ax=B ,未知量构成的矩阵(后者列向量)x=A\B 。
所以在MATLAB 中建立好矩阵就可以求解了,节约了运算时间,以上例子都是手工带入数据整理方程组的,但注意的是:数据的值其实是取代的对应的元件,因此也可以用符号表示方法化简方程组后,编制M 文件,由MATLAB 带入数据进行运算.。
电气设备故障分析常用的方法1.状态分析法这是一种发生故障时依据电气设备所处的状态进行分析的方法。
电气设备的运行过程可以分解成若干个连续的阶段,这些阶段也可称为状态,如电动机工作过程可以分解成启动、运转、正转、反转、高速、低速、制动、停止等工作状态,电气故障总是发生于某一状态,而在这一状态中,各种元件又处于什么状态,如电动机启动时,哪些元件工作,那些触头闭合等,是我们分析故障的重要依据。
2.图形分析法电气设备图是用以描述电气设备的构成、原理、功能、供应装接和使用修理信息的依据。
分析电气设备必定要使用各类电气图,依据故障状况,从图形上进行分析。
电气设备图纸种类许多,如原理图、构造图、系统图、接线图、绽开图、位置图等。
分析电气故障时,经常要对各种图进行分析,并且要把握各种图与图之间的有机关系,如由接线图变换成电路图、由绽开图变换成原理图等。
3.单元分析法一个电气设备总是由若干单元构成的,每一个单元具有特定的功能。
从肯定意义上讲,电气设备故障意味着某功能的丢失,由此可判定故障发生的单元。
分析电气故障应将设备划分为单元(通常是按功能划分),进而确定故障的范围。
4.回路分析法电路中任一闭合的路径称为回路。
回路是构成电气设备电路的基本单元、分析电气设备故障,尤其是分析电路断路、短路故障时,经常需要找出回路中元件,导线及其联接点,以此确定故障的缘由和部位。
5.推理分析法电气设备中各组成和功能都有其内在联系,如联接挨次、动作挨次、电流流向、电压安排等都有其特定的规律,因而某一部件、组件、元件的故障必定影响其他部分,表现出特有的故障现象。
在分析电气故障时,经常需要从这一故障联系到对其它部分的影响,或由某一故障现象找出故障的根源。
这一过程就是规律推理过程,也就是推理分析法。
推理分析法又分为顺推理法和逆推理法。
6.简化分析法电气设备的组成部件、元件,虽然都是必需的,但从不同的角度去分析,总可以划分出主要的部件、元件和次要的部件、元件。
§2-6 回路分析法及网孔分析法
1、物理描述
回路分析法(loop-analysis method)的基本指导思想是用未知的回路电流
代替未知的支路电流来建立电路方程,以减少联立方程的元数。
对于只隶属于一个回路的支路,其电流即等于该支路所属回路的回路电流;
对于两个(或两个以上)回路的公共支路,其电流可按基尔霍夫电流定律求解。
对于平面电路,可以按网孔取独立回路,以网孔电流(mesh current)为变量
,按照基尔霍夫电压定律和元件方程列出网孔电压方程(简称网孔方程)。
这种方法称为网孔分析法(mesh-analysis method)。
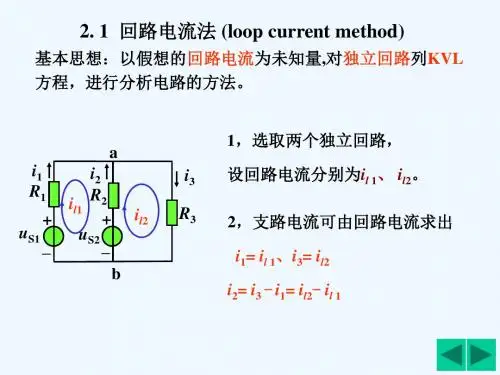
2 、现在以图2-6-1为例导出回路电流方程的一般式。
设想有两个电流i m1 ,i m2 分别沿着左右两个回路的边界连续流动,如果我们把i m1和i m2求出,则所有支路的电流均能以这两个电流表示而不再增设变量以减少联立方程的个数,这就是回路分析法。
i m1 ,i m2称作回路电流,那么支路电
流就可以表示成i1=i m1 i2=i m2 i1=i m1-i m2
图2-6-1 回路分析法示例
下面我们将导出回路分析法的一般式。
在图2-6-1 中有两个节点,三条支路,三个回路,两个网孔,为了建立回路方程,我们选择如图所示的两个回路为研究对象。
首先选定各回路电流的参考方向并以此作为建立KVL 方程时的绕行方向,然后以回路电流为变量建立回路方程,按照此原则对图2-6-1 所示电路有:
(2-6-1 )
我们注意到了在列上述两个方程时可以全然不顾各支路电流的参考方向。
整理2-6-1 可得:
(2-6-2 )
式(2-6-2 )是以回路电流为求解对象的回路电流方程。
解式(2-6-2 )可得回路电流i m1 ,i m2 ,进而可得各支路电流i1 ,i2 ,i3。
我们只需解两个联立方程
便可算出3 个未知的支路电流。
可见在以回路电流为变量时可以减少联立方程的个数。
方程的数目应该等于独立回路数。
简便之处还不仅在于此,更重要的是我们可以应用观察法即能列出回路电流方程观察式(2-6-2 )所示方程组我们可得如下规律:
(1 )式(2-6-2 )(a) 式中i m1 和(b) 式中i m2 前面的系数分别是它们各自所在回路中所有电阻之和,我们称之为自电阻用R11、R22表示。
自电阻恒为正值。
(2 )(2-6-2 )(a) 式中i m2 和(b) 式中i m1前面的系数为两回路的共有
电阻,我们称之为互电阻,用和表示。
当两回路电流流过互电阻流向相反时,互电阻应为负。
反之,互电阻为正。
(3 )(2-6-2 )式右边为各回路所有电压源电压升的代数和,用和
表示。
当电压升与回路电流绕行方向一致时取正值;反之,取负值。
如在(2-
6-2 )式中,。
对图2-6-1 所示电路用通式表示时有
( 2-6-3 )
为统一起见,上式我们将互电阻前的“ + ”“ - ”号包括在互电阻中了。
我们
很容易将上式推广成一般式。
对一个具有n 个回路的电路,回路电流方程的一般式可以由式(2-6-3 )推广得到,即
( 2-6-4 )
回路法是建立在基尔霍夫电压定律和元件方程基础上的,它对于平面或非平面电路均适用。
为了建立网孔方程,应先在每一个网孔中选定网孔电流的参考方向,并以此
作为建立网孔方程的计算电压代数和及电位升代数和的参考方向,然后应用基尔霍夫电压定律列出网孔方程。
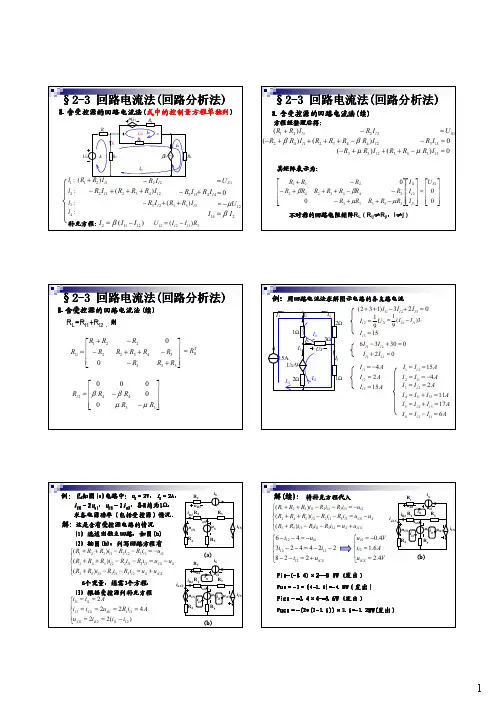
例2-6-1
例图2-6-1中各网孔方程依次
为(2-6-5)
(2-6-6)
(2-6-7)
经整理后变为
(2-6-8)
(2-6-9)
(2-6-10)
例2-6-1 回路分析法示例
再进一步写成便于推广应用的规范化形式
(2-6-11)
(2-6-12)
(2-6-13)
式中
是网孔1 中的各支路电阻的总和,称为网孔1的自电阻(self resistance);
是网孔2中的各支路电阻的总和,称为网孔2的自电阻;
是网孔3中的个支路电阻的总和,称为网孔3的自电阻
是网孔1和网孔2 的公共支路电阻的负值,称为网孔1和网孔2 的共电阻[或互电阻(mutual resistance)];
是网孔2和网孔3 的公共支路电阻的负值,称为网孔2和网孔3 的共电阻;
是网孔1和网孔3的公共支路电阻的负值,称为网孔1和网孔3的共电阻;
是网孔1中沿网孔参考方向的各电压源电位升的代数和;
是网孔2中沿网孔参考方向的各电压源电位升的代数和;
是网孔3中沿网孔参考方向的各电压源电位升的代数和;
网孔的自电阻恒为正值。
两网孔的共电阻则可以为正,也可以为负,视相邻
两网孔电流通过公共支路时其参考方向相同或相反而定。
当相邻两网孔电流以同一参考方向通过公共支路时,共电阻为正;反之,当相邻两网孔电流以相反的参考方向通过公共支路时,其共电阻为负。
计算一个网孔中电压源电位升的代数和时,凡电压源电位升的参考方向与该
网孔的参考方向一致者,在它的前面取“+”;反之,取“-”。
通常用回路(或网孔)分析法建立回路(或网孔)方程组时,可以先算出各
回路(或网孔的)自电阻、相关回路(或网孔)的共电阻和每一回路(或网孔)中电压源电位升的代数和,然后再写出方程组。
例2-6-2 、例2-6-3。