用超网孔分析法列、解含无伴电流源电路方程
- 格式:doc
- 大小:163.50 KB
- 文档页数:4






用超网孔分析法列、解含无伴电流源电路方程机电学院 刘祖云 张汉飞摘要:从探讨电路网孔的画法出发,对电路的网孔进行了扩展定义,提出了超网孔的概念。
运用超网孔分析无伴电流源电路简单易行,可以用观察法直接列出电路方程,而无需列约束方程或重新绘制电路图等,并使电路方程数量减少,求解方便。
关键词:网孔、超网孔、无伴电流源、电路分析、电路方程在电路分析中,网孔电流法因其列方程简单、列出的行列式具有对称性深受学生的喜爱。
但是当两网孔中间出现一个或多个无伴恒流源时,其网孔方程变得不太明了,不能用观察的方法直接列出;回路电流法对回路的选择具有灵活性,可以任意列出任何电路的KVL 方程,但由于列出的电路方程组一般不具备对称性,出错后不方便查找错误,因此一般不太受学生欢迎。
1、 网孔分析法中无伴电流源的处理办法采用“电流源支路单相关”法。
我们知道,一条支路最多可以和两个网孔相关联,也可以只和一个网孔相关联。
这种一条支路只作为一个网孔边界的情况称为“单相关”。
和网孔单相关的支路显然都是电路最外沿的支路,每一单相关支路中流过的是与它关联的网孔电流。
这就意味着,如果一个理想电流源支路是单相关支路,则它所在网孔的电流便是已知的,于是该网孔的方程就不需列写,这样便减少了方程的数目。
这种方法称为“电流源支路单相关”法。
如果理想电流源支路在电路中是两个网孔的公共支路,则往往能通过用改画电路图的方法将双相关的恒流源改画成单相关恒流源。
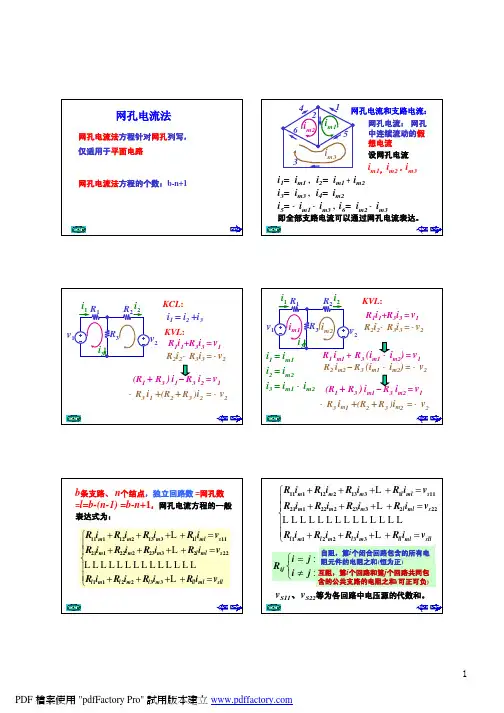
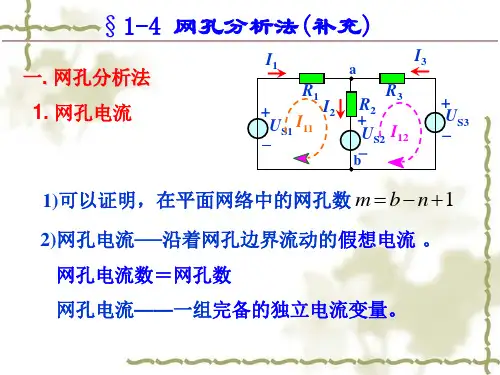
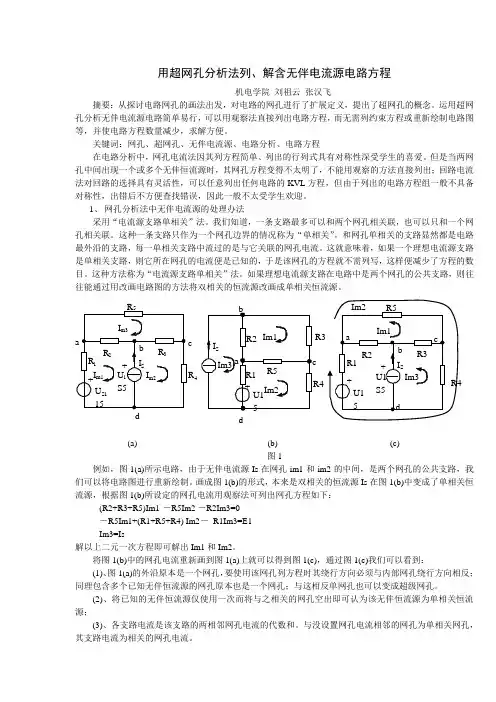
(a)(b) (c)图1例如,图1(a)所示电路,由于无伴电流源Is 在网孔im1和im2的中间,是两个网孔的公共支路,我们可以将电路图进行重新绘制。
画成图1(b)的形式,本来是双相关的恒流源Is 在图1(b)中变成了单相关恒流源,根据图1(b)所设定的网孔电流用观察法可列出网孔方程如下:(R2+R3+R5)Im1 -R5Im2 -R2Im3=0 -R5Im1+(R1+R5+R4) Im2- R1Im3=E1Im3=Is解以上二元一次方程即可解出Im1和Im2。

用矩阵方法使网孔分析法通解黄明康 5030309754 F0303025在网络电路的学习中,我们一般使用结点分析法与网孔分析法。
我们知道他们有各自的用途,但其实如果使用得当,只用其中的一个方法就可以解所有目前已经可解得网络电路。
而在我看来这得当的使用就是巧妙运用数学。
之所以如此,我认为是因为结点分析法的基础KCL与网孔分析法的基础KVL是相容的,即可以用结点分析法的地方就可以用网孔分析法解题。
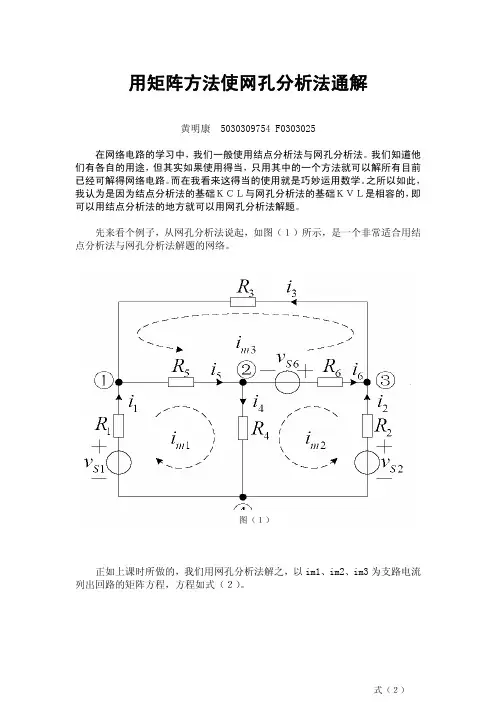
先来看个例子,从网孔分析法说起,如图(1)所示,是一个非常适合用结点分析法与网孔分析法解题的网络。
正如上课时所做的,我们用网孔分析法解之,以im1、im2、im3为支路电流列出回路的矩阵方程,方程如式(2)。
最左边的矩阵是各回路的电阻矩阵,解出此方程,再根据VCR就能得出整个网路电路的各个参数。
由于篇幅所限,也由于这已是大家皆知的常规方法,对于为何使用这种方法及其可用性、使用方法等在此不再冗述。
而我关心的是,这种方法是在这么一个可以说是完美的电路网络中运用的,所以一旦电路中的某个器件变了,可能使这种方法不可用。
而其实上课时已经提出了这种问题,也给出了改进了的解题方法——运用网路电路的一些性质化解电路成可用网孔分析法的电路。
但这种方法在解题中会使不熟练的我不经意中掉入“陷阱”。
我更愿意用以下的方法用数学解题,这样可以使我们不必太过计较概念。
对于我的方法,也请先看一个例子,如图(3):这样,这个电路就不能单纯的运用网孔分析法了。
那么按之前所述,运用网路电路的一些性质化解电路成可用网孔分析法的电路,然后解之,正如图(4)a 和图(4)b 中所示过程。
然后得出电阻网络矩阵方程,解出所要的量。
对于以上的例题,也有所谓的虚网孔电流法如式(5):其实,虚网孔电流法仅仅只是根据我们在网孔分析法的引出中得出的规律重新又列出了简单的方程组,这跟我们最初想要使用结点分析法和网孔分析法的初衷不符,初衷是按给出的网络电路图直接写出矩阵方程。
)/ 10 + (v –v )/ 10 + v / 50 + (v –v )/ 20 [1]Ref.1234Refresh and Exercise网孔1:-6 + 6i 1-2 = 0[1]网孔2: 2 + 15 i 2–12 i 3–1.5 = 0[2]网孔3:i 3= 0.1 v x [3]v x = 1×i 1 [4]i 1= 1.333 A. i 3= 0.1 v x = 0.1 i 1= 133.3 mA.132典型错误:电流源误为电压源第四章36题:求各网孔电流..kh d[1]1243 3 + 5000 i 2= 0[1][2]c o m11005.1i i i sc +=没有独立源,所以V TH = 0.添加1-A 电流源:v xv f·2.0)50200(01.0200=−×++×v i v 1=ab v A V V i testtest 75.0=+=w.kh .c o100×10-3= V / 250 + V / 7.5×103= 13(5) = 65 V.第四章12题:用节点分析法求电流i 5.节点1:-3 = v 1/3 + (v 1–v 2)/ 1[1]节点2: 2 = (v 2–v 1)/ 1 + (v 2–v 3)/ 3 + (v 2–v 4)/ 4[2]节点3: 3 = v 3/ 5 + (v 3–v 4)/ 7 + (v 3–v 2)/ 3[3]节点4:0 = v 4/ 6 + (v 4–v 3)/ 7 + (v 4–v 2)/ 4[4]Refresh and Exercise1234Ref.典型错误:标注混乱导致电流方向错误wk h d o m[1][2]1234+ 4700 i 1–4700 i 4= 0[1][2][3]+ 0.1 i = 0[4]1234典型错误:电流源误为电压源w.k h d o m课o010∠j25.0−j 4xIxVw.kh6∠-13ºV6Vj0.004Ω-j/0.0015Ω-j/0.002Ωw.k hChapter 11AC Circuit Power Analysis第11章20题:电路如图所示:(a)在a 点和b 点之间应接入怎样的阻抗Z L才能吸收最大平均功率?(b)最大平均功率是多少?P total = ½(41.61) ×(5) cos w.k h d 课w.k h d .c o m课量分析进行求解。
用超网孔分析法列、解含无伴电流源电路方程
机电学院 刘祖云 张汉飞
摘要:从探讨电路网孔的画法出发,对电路的网孔进行了扩展定义,提出了超网孔的概念。
运用超网孔分析无伴电流源电路简单易行,可以用观察法直接列出电路方程,而无需列约束方程或重新绘制电路图等,并使电路方程数量减少,求解方便。
关键词:网孔、超网孔、无伴电流源、电路分析、电路方程
在电路分析中,网孔电流法因其列方程简单、列出的行列式具有对称性深受学生的喜爱。
但是当两网孔中间出现一个或多个无伴恒流源时,其网孔方程变得不太明了,不能用观察的方法直接列出;回路电流法对回路的选择具有灵活性,可以任意列出任何电路的KVL 方程,但由于列出的电路方程组一般不具备对称性,出错后不方便查找错误,因此一般不太受学生欢迎。
1、 网孔分析法中无伴电流源的处理办法
采用“电流源支路单相关”法。
我们知道,一条支路最多可以和两个网孔相关联,也可以只和一个网孔相关联。
这种一条支路只作为一个网孔边界的情况称为“单相关”。
和网孔单相关的支路显然都是电路最外沿的支路,每一单相关支路中流过的是与它关联的网孔电流。
这就意味着,如果一个理想电流源支路是单相关支路,则它所在网孔的电流便是已知的,于是该网孔的方程就不需列写,这样便减少了方程的数目。
这种方法称为“电流源支路单相关”法。
如果理想电流源支路在电路中是两个网孔的公共支路,则往往能通过用改画电路图的方法将双相关的恒流源改画成单相关恒流源。
(a)
(b) (c)
图1
例如,图1(a)所示电路,由于无伴电流源Is 在网孔im1和im2的中间,是两个网孔的公共支路,我
们可以将电路图进行重新绘制。
画成图1(b)的形式,本来是双相关的恒流源Is 在图1(b)中变成了单相关恒流源,根据图1(b)所设定的网孔电流用观察法可列出网孔方程如下:
(R2+R3+R5)Im1 -R5Im2 -R2Im3=0 -R5Im1+(R1+R5+R4) Im2- R1Im3=E1
Im3=Is
解以上二元一次方程即可解出Im1和Im2。
将图1(b)中的网孔电流重新画到图1(a)上就可以得到图1(c),通过图1(c)我们可以看到:
(1)、图1(a)的外沿原本是一个网孔,要使用该网孔列方程时其绕行方向必须与内部网孔绕行方向相反;同理包含多个已知无伴恒流源的网孔原本也是一个网孔;与这相反单网孔也可以变成超级网孔。
(2)、将已知的无伴恒流源仅使用一次而将与之相关的网孔空出即可认为该无伴恒流源为单相关恒流源;
(3)、各支路电流是该支路的两相邻网孔电流的代数和。
与没设置网孔电流相邻的网孔为单相关网孔,其支路电流为相关的网孔电流。
R 4 c
c R3R4 d
2、 应用超网孔分析法列、解含无伴电流源电路实例详解
我们运用上面所提出的分析无伴电流源电路的新方法,来分析两个实际例题。
例1:求图2所示各支路电流
解:本电路有三个网孔,有两个电流为已知
电流因此只需选择一个未知网孔电流,两个已知网孔电流即可求解,解法如下:
设未知网孔为abdca ,可通过观察列出KVL 方程:
(2+3+4+5)Im1-(2+4) Im2-(4+5) Im3=0 将Im2=1、Im3=4代入上式得: 14 Im1=42 Im1=3
各支路电流如下: I1= -Im1=-3A
I2= Im1- Im2- Im3=-2A I3=I1+4=-3+4=1A
例2:求图3中所有支路的电流。
解:由图可以看出,此电路有8条支路,有4个网孔,有两个无伴恒流源,只需列二元一次方程就行了。
第一步:选择网孔,未知电流网孔由两个大的网
孔abcea 和aecda 组成,已知电流网孔由两个小的网孔bceb 和ecde 组成,绕行方向均选取顺时钟方向;
第二步:利用网孔法的规则列写电路方程:
1
211
7)12()1122()11(73)12()11()1122(4343214321==-=++-+++++--=-+++-+++m m m m m m m m m m i i i i i i i i i i
整理后得:
5
629
262121-=+--=-m m m m i i i i
由方程可以看出,此方程与网孔方程的形式是一样的具有对称性;
第三步:解此方程得:
A
i A i m m 5.1221-=-=
第四步:根据电流关系求各支路电流: I1=Im1=-2A; I2=Im2=-1.5A;
5 Ω
图2 例1图
I3
I6
c
图3
I3=I1+2=0A; I4=I2-I1=0.5A; I5=I4+1-2=-0.5A; I6=-(I2+1)=0.5A
3、应用超网孔分析法列、解含无伴电流源电路的基本步骤
通过上面的实例分析,可以将超网孔分析法列、解含无伴电流源电路的基本步骤归纳如下: (1) 将待求电路化分为几个排列有序的未知电流网孔,该未知电流网孔可包含若干已知恒流源网
孔; (2) 将已知的恒流源网孔分别单独列出;
(3) 用观察法按网孔电流方程规则列写网孔方程;
(4) 求解网孔方程;
(5) 根据已解出的网孔电流求解各支路电流。
例3、求解如图4所示电路电流I
解:第一步,将电路化简,与恒流源串联的电阻可视为短路,与恒压源并联的电阻可祝为开路。
化简后的电路图如图5所示,该图有7个网孔,有4个已知无伴恒流源,因此只要列3个未知网孔电流就行了,3个未知网孔电流用实线箭头表示,已知的网孔电流用虚线箭头表示,可用观察法列出方程如下:
1.5Ω 图4
(2+2+1+1+1+4)Im1-2Im2-2Im3-(1+1+1)×2-(1+2+2)×5-(1+1+2+2)×3+4×1=-12+1+1 -2Im1+4 Im2+10+6=4 -2 Im1+4Im3+10+6=-4 整理后得:
11Im1 -2Im2 -2Im3 =35 -2Im1 +4Im2 =-12 -2 Im1 +4Im3
=-20
解此方程组得: Im1=2.111A Im2=-1.944A Im3=-3.944A I=im1-2=0.111A
4、结论
应用超网孔分析法列、解含无伴电流源电路,结合了无伴电流源电路的特点,很方便地列出电路方程,并且和传统的电路分析方法相比,大大减少了列方程的数量,是一种分析无伴电流源电路的新方法。
12V
图5。