河南省实验中学2009—2010学年八年级上数学期中试卷及答案

河南省实验中学2014--2015学年上期期中试卷 八年级 物理 命题人 尚翠娇 审题人 谢虹燕（时间：60分钟 满分：70分）注意事项：1.本试卷共6页，五大题，25小题，满分70分，考试时间60分钟。

2.请用黑色的签字水笔将答案填写在答题卡的相应位置上，答在试卷上无效。

一、填空题（本大题共8小题，每小题2空，每空1分，共16分） 1.雨季来临河面水位上涨，停泊在河面上的船身也随之“水涨船高”，在船升高这个运动过程中，描述船的位置升高是以 为参照物，若以 为参照物，则船是静止的。

2.测量如图1所示的某物体长度，所使用的刻度尺的分度值 为 ，测量结果是 。

3.声呐是一种利用 （选填“超声波”、“次声波”或“声音”）可以在 传播的原理来工作，从而实现对水 下目标进行探测、定位和通信的电子设备，已经成为各国海军进行水下检测使用的主要技术了。

4.温度计是利用液体的 原理制成的，如图2是一支体温 计，有位同学很粗心拿着它没有向下甩就直接给另一位同学测量体 温，若被测同学的实际体温为36℃，则测量结果将是℃。

5.每年12月末至春节前的一段时间，是位于吉林松原的查干湖一 年一度的冬捕季节，也是渔民进行大规模冬季捕鱼作业的黄金时间，冰封雪域的湖面上“人欢鱼跃”一派丰收景象,如图3所示,假如冰面上的温度低达－40℃，那么在冰下流动的河水与冰交界处的温度是 ，图片上的主持人说话的同时也在呼出大 量“白气”，白气的成因是 （填写物态变化的名称）。

6.噪声是现代社会科技发展带来的公害之一，为了保护环境还给居民安宁，人们想出了各种方法为求减弱噪声，如图4甲、乙所示是常见的减弱噪声的方法，它们分别 表示在 和 减弱噪声。

7．晚上，在桌面上铺一张白纸，把一块小平面镜平放在纸上，让手电筒的光正对着平面镜照射，从侧面看去，则白纸比较______(填“亮”或 “暗”)，因为光在白纸上发生_____ 反射的现象。

图1 图2 图3 图48.针对实验现象，请把解决问题的方法填写在表中对应的空格里。

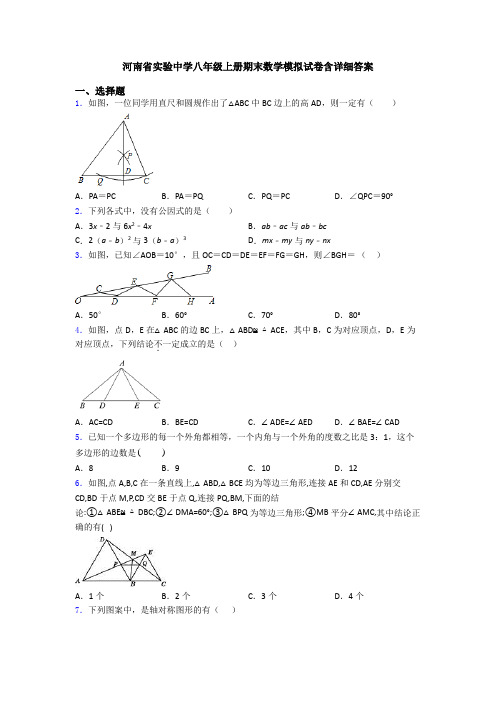
河南省实验中学八年级上册期末数学模拟试卷含详细答案一、选择题1．如图，一位同学用直尺和圆规作出了△ABC中BC边上的高AD，则一定有（）A．PA＝PC B．PA＝PQ C．PQ＝PC D．∠QPC＝90°2．下列各式中，没有公因式的是（）A．3x﹣2与6x2﹣4x B．ab﹣ac与ab﹣bcC．2（a﹣b）2与3（b﹣a）3D．mx﹣my与ny﹣nx3．如图，已知∠AOB＝10°，且OC＝CD＝DE＝EF＝FG＝GH，则∠BGH＝（）A．50°B．60°C．70°D．80°4．如图，点D，E在△ABC的边BC上，△ABD≌△ACE，其中B，C为对应顶点，D，E为对应顶点，下列结论不．一定成立的是（）A．AC=CD B．BE=CD C．∠ADE=∠AED D．∠BAE=∠CAD 5．已知一个多边形的每一个外角都相等，一个内角与一个外角的度数之比是3：1，这个多边形的边数是()A．8 B．9 C．10 D．126．如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面的结论:①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,其中结论正确的有( )A．1个B．2个C．3个D．4个7．下列图案中，是轴对称图形的有（）A ．1个B ．2个C ．3个D ．4个 8．若ABC 的三边a ，b ，c 满足()()0)(a b b c c a ---=那么ABC 的形状一定是（ ）．A ．等腰三角形B ．直角三角形C ．等边三角形D ．锐角三角形9．下列图形具有稳定性的是（ ）A ．B ．C ．D ．10．下列属于最简分式的是（ ）A ．()2211x x -- B ．233x x + C ．211x x +- D ．1751x二、填空题11．如图，//AB CD ，BP 和CP 分别平分∠ABC 和∠DCB ，AD 过点P ，且与AB 垂直．若AD=8，则点P 到BC 的距离是_________．12．已知：AD 、AE 分别是ABC 的高，中线，6BE =，4CD =，则DE 的长为_________．13．如图，在等边△ABC 中，D 、E 分别是AB 、AC 上的点，且AD=CE ，则∠BCD+∠CBE= 度．14．当a =____________时，分式44a a --的值为零．15．如图，ABC 的三边,,AB BC CA 的长分别为30,40,15，点P 是ABC 三个内角平分线的交点，则::PAB PBC PCA S S S =_____．16．已知一个等腰三角形的两边长分别为3和6，则等腰三角形的周长是_____．17．如图，直线AB ∥CD ，直线EF 分别与直线AB 和直线CD 交于点E 和F ，点P 是射线EA 上的一个动点（P 不与E 重合）把△EPF 沿PF 折叠，顶点E 落在点Q 处，若∠PEF=60°,且∠CFQ :∠QFP=2:5，则∠PFE 的度数是_______．18．如图，已知：∠BAC 的平分线与BC 的垂直平分线相交于点D ，DE ⊥AB ，DF ⊥AC ，垂足分别为E 、F ，AB ＝6，AC ＝3，则BE ＝_______．19．从A 沿北偏东60︒的方向行驶到B ，再从B 沿南偏西20︒方向行驶到C ，则ABC ∠=______.20．如图所示，在ABC ∆中，90C ∠=︒，AD 平分BAC ∠，DE AB ⊥于E ，8BC cm =，则DE DB +=________．三、解答题21．先化简221211111a a a a a a ⎛⎫-+-+÷ ⎪++-⎝⎭，再选择一恰当的a 的值代入求值． 22．设2244322M x xy y x y =-+-+，则M 的最小值为______．23．如图，B 、C 、E 三点在同一条直线上，AC ∥DE ，AC=CE ，∠ACD=∠B ．（1）求证：BC=DE（2）若∠A=40°，求∠BCD 的度数．24．如图，已知六边形ABCDEF 的每个内角都相等，连接AD .（1）若148∠=︒，求2∠的度数；（2）求证：//AB DE .25．先化简，再求值：2()()(2)()x y x y y x y x y +-++--，其中3x =，13y =-．26．（1）解方程组：202321x y x y -=⎧⎨+=⎩． （2）解不等式组：202(21)15x x x-<⎧⎨-≤+⎩． （3）分解因式：3x x -．（4）分解因式：221x x -++．27．先化简，再求值：22(4)(4)516ab ab a b ab ⎡⎤+--+÷⎣⎦，其中10a =，34b =． 28．已知x ＝3+1，y ＝3﹣1，求：（1）代数式xy 的值；（2）代数式x 3+x 2y +xy 2+y 3的值．29．如图，AC 平分∠BCD ，AB ＝AD ，AE ⊥BC 于E ，AF ⊥CD 于F .(1)若∠ABE ＝60°，求∠CDA 的度数；(2)若AE ＝2，BE ＝1，CD ＝4.求四边形AECD 的面积．30．如图，//AB CD ，点E 在直线CD 上，射线EF 经过点,B BG ，平分ABE ∠交CD 于点G ．（1）求证：BGE GBE ∠=∠；（2）若70∠︒=DEF ，求FBG ∠的度数．【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【解析】【分析】利用基本作法，作了线段CQ 的垂直平分线，则根据线段垂直平分线的性质可对各选项进行判断．【详解】由作法得AD 垂直平分CQ ，所以PQ ＝PC ．故选C ．【点睛】本题考查了作图-基本作图：熟练掌握5种基本作图（作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线）．2．B解析：B【解析】【分析】根据公因式的定义逐一分析即可．【详解】解：A 、6x 2﹣4x ＝2x （3x ﹣2），3x ﹣2与6x 2﹣4x 有公因式（3x ﹣2），故本选项不符合题意；B 、ab ﹣ac ＝a （b ﹣c ）与ab ﹣bc ＝b （a ﹣c ）没有公因式，故本选项符合题意；C 、2（a ﹣b ）2与3（b ﹣a ）3有公因式（a ﹣b ）2，故本选项不符合题意；D、mx﹣my＝m（x﹣y），ny﹣nx＝﹣n（x﹣y），mx﹣my与ny﹣nx有公因式（x﹣y），故本选项不符合题意．故选：B．【点睛】本题考查了公因式，熟悉因式分解是解题的关键．3．B解析：B【解析】【分析】根据三角形外角和内角的关系以及等腰三角形的性质，逐步推出∠BGH的度数．【详解】解：∵∠AOB＝10°，OC＝CD＝DE＝EF＝FG＝GH，∴∠ODC=10°，∴∠BCD=∠AOB+∠ODC=20°，∵CD=DE，∴∠DEC=∠BCD=20°，∴∠ADE=∠CED+∠AOB=30°，∵ED=EF，∴∠EFD=30°，∴∠BEF=∠EFD+∠AOB=40°，∵FE=FG，∴∠FGE=40°，∴∠GFH=∠FGE+∠AOB=50°，∵GF=GH，∴∠GHF=50°，∴∠BGH=∠GHF+∠AOB=60°，故选B．【点睛】本题综合考查了等腰三角形的性质、三角形外角性质．此类题考生应该注意的是外角性质的运用．4．A解析：A【解析】【分析】【详解】∵△ABD≌△ACE，∴∠ADB=∠AEC，∠BAD=∠CAE，BD=CE，∴180°-∠ADB=180°-∠AEC，∠BAD+∠DAE=∠CAE+∠DAE，BD+DE=CE+DE，即∠ADE=∠AED，∠BAE=∠CAD，BE=CD，故B、C、D选项成立，不符合题意；无法证明AC=CD，故A符合题意，故选A.5．A解析：A【解析】试题分析：设这个多边形的外角为x°，则内角为3x°，根据多边形的相邻的内角与外角互补可的方程x+3x=180，解可得外角的度数，再用外角和除以外角度数即可得到边数．解：设这个多边形的外角为x°，则内角为3x°，由题意得：x+3x=180，解得x=45，这个多边形的边数：360°÷45°=8，故选A．考点：多边形内角与外角．6．D解析：D【解析】试题分析：∵△ABD、△BCE为等边三角形，∴AB=DB，∠ABD=∠CBE=60°，BE=BC，∴∠ABE=∠DBC，∠PBQ=60°，在△ABE和△DBC中，，∴△ABE≌△DBC（SAS），∴①正确；∵△ABE≌△DBC，∴∠BAE=∠BDC，∵∠BDC+∠BCD=180°﹣60°﹣60°=60°，∴∠DMA=∠BAE+∠BCD=∠BDC+∠BCD=60°，∴②正确；在△ABP和△DBQ中，，∴△ABP≌△DBQ（ASA），∴BP=BQ，∴△BPQ为等边三角形，∴③正确；∵∠DMA=60°，∴∠AMC=120°，∴∠AMC+∠PBQ=180°，∴P、B、Q、M四点共圆，∵BP=BQ，∴BP BQ，∴∠BMP=∠BMQ，即MB平分∠AMC；∴④正确；综上所述：正确的结论有4个；故选D．考点：等边三角形的性质与判定、全等三角形的判定与性质、四点共圆、圆周角定理．7．B解析：B【解析】【分析】根据轴对称图形的概念对各图形分析判断即可得解．【详解】第一个图形不是轴对称图形，第二个图形不是轴对称图形，第三个图形是轴对称图形，第四个图形是轴对称图形，综上所述，是轴对称图形的有2个．故选：B．【点睛】本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．8．A解析：A【解析】试题解析：∵（a-b）（b-c）（c-a）=0，∴（a-b）=0或（b-c）=0或（c-a）=0，即a=b或b=c或c=a，因而三角形一定是等腰三角形．故选A．9．A解析：A【解析】【分析】根据三角形具有稳定性，四边形具有不稳定性进行判断．【详解】解：三角形具有稳定性．故选：A．【点睛】本题考查了三角形的稳定性和四边形的不稳定性．10．B解析：B【解析】【分析】最简分式的分子和分母中不含能在约分的因数或因数，根据定义解答.【详解】A 、()2211x x --=()221111x x x x --=-+，故该项不符合题意； B 、233x x +不能化简，故该项符合题意； C 、211x x +-=21111x x x +-=---，故该项不符合题意； D 、1751x =13x，故该项不符合题意； 故选：B .【点睛】此题考查最简分式的定义，正确理解定义并能分解因式化简分式是解题的关键.二、填空题11．4【解析】【分析】如图（见解析），先根据平行线的性质可得，再根据角平分线的性质可得，然后根据线段的和差即可得．【详解】如图，过点P 作于点Q ，则PQ 即为所求，，，，BP 和CP 分别平分和解析：4【解析】【分析】如图（见解析），先根据平行线的性质可得AD CD ⊥，再根据角平分线的性质可得,PQ AP PQ DP ==，然后根据线段的和差即可得．【详解】如图，过点P 作PQ BC ⊥于点Q ，则PQ 即为所求，//AB CD ，AD AB ⊥，AD CD ∴⊥，BP 和CP 分别平分ABC ∠和DCB ∠，,PQ AP PQ DP ∴==，8AD AP DP =+=，28PQ ∴=，解得4PQ =，即点P 到BC 的距离是4，故答案为：4．【点睛】本题考查了平行线的性质、角平分线的性质等知识点，熟练掌握角平分线的性质是解题关键．12．2或10【解析】【分析】由已知条件，可推导出；再假设D 点所在的不同位置，分别计算，即可得到答案．【详解】∵是的中线，且∴假设点D 在CB 的延长线上，如下图∵是的中线，且∴∵∴解析：2或10【解析】【分析】由已知条件，可推导出6EC BE ==；再假设D 点所在的不同位置，分别计算DE ，即可得到答案．【详解】∵AE 是ABC 的中线，且6BE =∴6EC BE ==假设点D 在CB 的延长线上，如下图∵AE 是ABC 的中线，且6BE =∴212BC BE ==∵4CD =∴CD BC <，和图形不符∴该假设不成立；假设点D 在点E 和点B 之间，如下图∵4CD =，6EC =∴CD EC <，和图形不符∴该假设不成立；假设点D 在点E 和点C 之间，如下图∴642DE EC CD =-=-=；假设点D 在点BC 延长线上，如下图∴6410DE EC CD =+=+=；故答案为：2或10．【点睛】本题考察了三角形中线和三角形高的知识；求解的关键是熟练掌握三角形中线和三角形高的性质，从而完成求解．13．【解析】试题分析：根据等边三角形的性质，得出各角相等各边相等，已知AD=CE，利用SAS判定△ADC≌△CEB，从而得出∠ACD=∠CBE，所以∠BCD+∠CBE=∠BCD+∠ACD=∠ACB=解析：【解析】试题分析：根据等边三角形的性质，得出各角相等各边相等，已知AD=CE，利用SAS判定△ADC≌△CEB，从而得出∠ACD=∠CBE，所以∠BCD+∠CBE=∠BCD+∠ACD=∠ACB=60°．解：∵△ABC是等边三角形∴∠A=∠ACB=60°，AC=BC∵AD=CE∴△ADC≌△CEB∴∠ACD=∠CBE∴∠BCD+∠CBE=∠BCD+∠ACD=∠ACB=60°．故答案为60．考点：等边三角形的性质；全等三角形的判定与性质．14．-4【解析】【分析】分式的值为零时,分子等于零,分母不等于零,进行求解即可．【详解】解：∵分式的值为零,∴．解得：,所以当时,分式无意义,故舍去．综上所述,．故答案为：-4．解析：-4【解析】【分析】分式的值为零时,分子等于零,分母不等于零,进行求解即可．【详解】解：∵分式44aa--的值为零,∴4=0a-．解得：=4a,所以=4a ±当=4a 时,分式无意义,故舍去．综上所述,=4a -．故答案为：-4．【点睛】考查了分式的值为零的条件,注意：“分母不为零”这个条件不能少．15．【解析】【分析】过P 作PD⊥AB 于D ，PE⊥BC 于E ，PF⊥AC 于F ，根据角平分线性质求出PD=PE=PF ，根据三角形面积公式求出即可．【详解】解：如图，过P 作PD⊥AB 于D ，PE⊥BC 于解析：6:8:3【解析】【分析】过P 作PD ⊥AB 于D ，PE ⊥BC 于E ，PF ⊥AC 于F ，根据角平分线性质求出PD=PE=PF ，根据三角形面积公式求出即可．【详解】解：如图，过P 作PD ⊥AB 于D ，PE ⊥BC 于E ，PF ⊥AC 于F ，∵P 为△ABC 三条角平分线的交点，∴PD=PE=PF ，∵△ABC 的三边AB ，BC ，CA 的长分别为30，40，15，∴::PAB PBC PCA S S S 111::222AB PD BC PE AC PF ⎛⎫⎛⎫⎛⎫=⨯⨯⨯⨯⨯⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=AB ：BC ：AC=30：40：15=6：8：3．故答案为：6：8：3．【点睛】本题考查了三角形的面积，角平分线性质的应用，掌握角的平分线上的点到角的两边的距离相等是解题的关键．16．15【解析】【分析】分腰为3和腰为6两种情况考虑，先根据三角形的三边关系确定三角形是否存在，再根据三角形的周长公式求值即可．【详解】解：当腰为3时，3+3=6，∴3、3、6不能组成三角形解析：15【解析】【分析】分腰为3和腰为6两种情况考虑，先根据三角形的三边关系确定三角形是否存在，再根据三角形的周长公式求值即可．【详解】解：当腰为3时，3+3=6，∴3、3、6不能组成三角形；当腰为6时，3+6=9＞6，∴3、6、6能组成三角形，该三角形的周长为=3+6+6=15．故答案为：15．【点睛】本题考查了等腰三角形的性质以及三角形三边关系，由三角形三边关系确定三角形的三条边长为解题的关键．17．50°【解析】【分析】依据平行线的性质，即可得到∠EFC的度数，再求出∠CFQ，即可求出∠PFE的度数．【详解】∵AB∥CD，∠PEF＝60°，∴∠PEF+∠EFC＝180°，∴∠EF解析：50°【解析】【分析】依据平行线的性质，即可得到∠EFC的度数，再求出∠CFQ，即可求出∠PFE的度数．【详解】∵AB∥CD，∠PEF＝60°，∴∠PEF+∠EFC＝180°，∴∠EFC＝180°﹣60°＝120°，∵将△EFP沿PF折叠，便顶点E落在点Q处，∴∠PFE＝∠PFQ，∵∠CFQ:∠QFP=2:5∴∠CFQ＝212∠EFC＝212×120°＝20°，∴∠PFE＝12∠EFQ＝12（∠EFC﹣∠CFQ）＝12（120°﹣20°）＝50°．故答案为：50°．【点睛】本题主要考查了平行线的性质以及翻折问题的综合应用，正确掌握平行线的性质和轴对称的性质是解题的关键．18．【解析】【分析】连接CD、BD，由∠BAC的平分线与BC的垂直平分线相较于点D，DE⊥AB，DF⊥AC，根据角平分线的性质与线段垂直平分线的性质，易得CD=BD，DF=DE，从而得到AF=AE解析：3 2【解析】【分析】连接CD、BD，由∠BAC的平分线与BC的垂直平分线相较于点D，DE⊥AB，DF⊥AC，根据角平分线的性质与线段垂直平分线的性质，易得CD=BD，DF=DE，从而得到AF=AE，可证的Rt△CDF≌Rt△BDE，则可得BE=CF，即可得到结果．【详解】解：如图所示，连接CD、BD，∵AD是∠BAC的平分线，DE⊥AB，DF⊥AC，∴DF=DE，∠F=∠DEB=90°，∠ADF=∠ADE，∴AE=AF，∵DG是BC的垂直平分线，∴CD=BD，在Rt △CDF 和Rt △BDE 中CD BD DF DE=⎧⎨=⎩ ∴Rt △CDF ≌Rt △BDE∴BE=CF ，∴AB=AE+BE=AF+BE=AC+CF+BE=AC+2BE ，∵AB=6，AC=3，∴BE=32． 故答案为：32 【点睛】本题主要考查的是线段垂直平分线的性质、角平分线的性质以及全等三角形的判定与性质，掌握以上知识点是解题的关键．19．40【解析】【分析】根据方位角的概念，画图正确表示出行驶的过程，再根据已知转向的角度结合三角形的内角和与外角的关系求解．【详解】如图，A 沿北偏东60°的方向行驶到B ，则∠BAC=90°-解析：40【解析】【分析】根据方位角的概念，画图正确表示出行驶的过程，再根据已知转向的角度结合三角形的内角和与外角的关系求解．【详解】如图，A 沿北偏东60°的方向行驶到B ，则∠BAC=90°-60°=30°，B 沿南偏西20°的方向行驶到C ，则∠BCO=90°-20°=70°，又∵∠ABC=∠BCO-∠BAC ，∴∠ABC=70°-30°=40°．故答案为40°【点睛】解答此类题需要从运动的角度，正确画出方位角，再结合三角形的内角和与外角的关系求解．20．【解析】【分析】由角平分线的性质定理，得到CD=DE ，然后等量代换即可得到答案．【详解】解：∵在中，，∴DC⊥AC，∵平分，，∴CD=DE，∴；故答案为：8cm ；【点睛】本题解析：8cm【解析】【分析】由角平分线的性质定理，得到CD=DE ，然后等量代换即可得到答案．【详解】解：∵在ABC ∆中，90C ∠=︒，∴DC ⊥AC ，∵AD 平分BAC ∠，DE AB ⊥，∴CD=DE ，∴8DE DB CD DB CB +=+==；故答案为：8cm ；【点睛】本题考查了角平分线的性质定理，解题的关键是熟练掌握角平分线的性质定理，正确得到CD=DE ．三、解答题21．1a a -；a =0时，原式=0 【解析】【分析】根据分式的运算法则即可求出答案．【详解】解：原式=（11a ++11a a -+）•11a a +- =1a a +•11a a +- =1a a - ∵2101010a a a +≠⎧⎪-≠⎨⎪-≠⎩， ∴a ≠±1，∴把a =0代入得：原式=0．【点睛】本题考查了分式的运算，解题的关键是运用分式的运算法则，本题属于基础题型．22．38- 【解析】【分析】把M 化成完全平方的形式，再示出其最小值即可．【详解】2244322M x xy y x y =-+-+22112224x y y y ⎛⎫=--++- ⎪⎝⎭ 22111132224488x y y ⎛⎫⎛⎫=--++--≥- ⎪ ⎪⎝⎭⎝⎭ 当且仅当14y =-，316x =表达式取得最小值． 故答案为：38-． 【点睛】考查了完全平方公式，解题关键是把整式化成完全平方的形式．23．（1）证明见解析；（2）140°；【解析】【分析】（1）根据平行线的性质可得∠ACB=∠DEC ，∠ACD=∠D ，再由∠ACD=∠B 可得∠D=∠B ，然后可利用AAS 证明△ABC ≌△CDE ，进而得到CB=DE ；（2）根据全等三角形的性质可得∠A=∠DCE=40°，然后根据邻补角的性质进行计算即可．【详解】（1）∵AC ∥DE ，∴∠ACB=∠DEC，∠ACD=∠D，∵∠ACD=∠B．∴∠D=∠B，在△ABC和△DEC中，===ACB EB DAC CE∠∠⎧⎪∠∠⎨⎪⎩，∴△ABC≌△CDE（AAS），∴BC=DE；（2）∵△ABC≌△CDE，∴∠A=∠DCE=40°∴∠BCD=180°–40°=140°．【点睛】本题考查的是全等三角形，熟练掌握全等三角形的性质是解题的关键.24．(1)248∠=︒；（2）证明见解析；【解析】【分析】（1）先求六边形ABCDEF的每个内角的度数，再根据四边形的内角和是360°，求∠2的度数．（2）由（1）中∠ADC的度数，可得∠BAD=∠ADE，利用内错角相等，两直线平行，可证AB∥DE．【详解】（1）∵六边形ABCDEF的每个内角的度数是（6-2）×180°÷6=120°∴∠FAB=120°,∵∠1=48°∴∠FAD=∠FAB-∠1=120°-48°=72°,∴∠2=360°-120°-120°-72°=48°．（2）∵∠1=48°,∠2=48°，∴AB∥DE．【点睛】正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键，不能遇到相等或互补关系的角就误认为具有平行关系，只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行．注意平行于同一条直线的两直线平行．25．3xy，3-．【解析】【分析】先计算平方差公式、完全平方公式、整式的乘法，再计算整式的加减法，然后将x、y的值代入即可得．【详解】原式222222(2)x y xy y x xy y =-++--+，2222222x y xy y x xy y =-++-+-，3xy =，将3x =，13y =-代入得：原式133333xy ⎛⎫==⨯⨯-=- ⎪⎝⎭．【点睛】本题考查了平方差公式、完全平方公式、整式的加减法与乘法，熟记公式和整式的运算法则是解题关键． 26．（1）63x y =⎧⎨=⎩；（2）32x -≤<；（3）()()11x x x +-；（4）()21x - 【解析】【分析】（1）加减消元法解方程组；（2）先分别解不等式，再找解集的公共部分；（3）先提公因式，再用平方差公式；（4）应用完全平方公式．【详解】（1）解：202321x y x y -=⎧⎨+=⎩①②， ②－①×2，得：721y =，解得：3y =，把3y =代入①得：6x =，∴原方程组的解为：63x y =⎧⎨=⎩； （2）解：202(21)15x x x -<⎧⎨-≤+⎩①②， 由①得：2x ＜，由②得：4-215x x ≤+，解得：3x ≥-，∴原不等式组的解为：32x -≤<；（3）原式＝()()()211-1x x x x x -=+； （4）原式＝221x x -++＝()21x -．【点睛】本题考查二元一次方程组的解法，一元一次不等式组的解法，因式分解的方法，熟练掌握基础知识是关键．27．4ab -；﹣30【解析】【分析】原式括号内先根据平方差公式计算，再合并同类项，然后计算除法，最后把a 、b 的值代入化简后的式子计算即可．【详解】解：原式=222216516a b a b ab ⎡⎤--+÷⎣⎦=224a b ab -÷=4ab -；当10a =，34b =时，原式=3410304-⨯⨯=-． 【点睛】本题考查了整式的混合运算和代数式求值，属于基本题型，熟练掌握整式的混合运算法则是解题的关键．28．（1）2；（2）【解析】【分析】（1）直接代入平方差公式计算即可；（2）先计算出x+y 和x 2+y 2,原式整理成（x 2+y 2）（x+y ）代入计算即可；【详解】（1）xy=）=2-1=2；（2）∵x ，y 1，xy=2,∴∴x 2+y 2=（x+y ）2-2xy=8，则x 3+x 2y +xy 2+y 3= x 2（x+y ）+y 2（x+y ）=（x 2+y 2）（x+y ）【点睛】此题考查整式的化简求值，平方差公式，完全平方公式，解题关键在于掌握运算法则.29．（1）120°；（2）9.【解析】【分析】(1)、根据角平分线的性质以及AB=AD 得出Rt △ABE 和Rt △ADF 全等，从而得出∠ADF ＝∠ABE ＝60°，根据平角得出∠ADC 的度数；(2)、根据三角形全等得出FD ＝BE ＝1，AF ＝AE ＝2，CE ＝CF ＝CD ＋FD ＝5，最后根据S 四边形AECD ＝S △AEC ＋S △ACD 得出答案．【详解】解：(1)∵AC 平分∠BCD ，AE ⊥BC ，AF ⊥CD ，∴∠ACE ＝∠ACF ，∠AEC ＝∠AFC ＝90°，∴AE ＝AF ，在Rt △ABE 和Rt △ADF 中，AE=AF ，AB=AD ，∴Rt △ABE ≌Rt △ADF(HL)，∴∠ADF ＝∠ABE ＝60°，∴∠CDA ＝180°－∠ADF ＝120°；(2)由(1)知Rt △ABE ≌Rt △ADF ，∴FD ＝BE ＝1，AF ＝AE ＝2，在△AEC 和△AFC 中，∠ACE=∠ACF，∠AEC=∠AFC，AC=AC ，∴△AEC ≌△AFC(AAS)，∴CE ＝CF ＝CD ＋FD ＝5，∴S 四边形AECD ＝S △AEC ＋S △ACD ＝12EC·AE ＋12CD·AF ＝12×5×2＋12×4×2＝9． 【点睛】本题主要考查的是角平分线的性质、三角形全等的应用以及三角形的面积计算，难度中等．理解角平分线上的点到角两边的距离相等的性质是解决这个问题的关键．30．（1）见解析；（2）145°【解析】【分析】（1）根据//AB CD ，可得ABG BGE ∠=∠，根据BG 平分ABE ∠，可得ABG GBE ∠=∠，进而可得BGE GBE ∠=∠； （2）根据//AB CD ，可得70ABE DEF ∠=∠=︒，根据平角定义可得180110ABF ABE ∠=︒-∠=︒，根据BG 平分ABE ∠，可得1352ABG ABE ∠=∠=︒，进而可得FBG ∠的度数．【详解】解：（1）证明：//AB CD ，ABG BGE ∴∠=∠， BG 平分ABE ∠，ABG GBE ∴∠=∠，BGE GBE ∴∠=∠；（2）//AB CD ，70ABE DEF ∴∠=∠=︒，180110ABF ABE ∴∠=︒-∠=︒， BG 平分ABE ∠，1352ABG ABE ∴∠=∠=︒， 11035145FBG ABF ABG ∴∠=∠+∠=︒+︒=︒．答：FBG ∠的度数为145︒．【点睛】本题考查了平行线的性质，解决本题的关键是掌握平行线的性质．。

2009——2010学年度八年级第一学期期中考试数 学 试 卷一、填空题（每题3分，共30分）1．在722，4，39， 141414.3-，π-， 2323323332.0，023⎪⎪⎭⎫ ⎝⎛中无理 是 个。

2．在Rt △ABC 中，斜边AB=2，则AB 2+BC 2+AC 2= . 3= 。

25-的倒数为 。

4．一条线段AB 的长是3cm ，将它沿水平方向平移4cm 得到线段CD ，则CD 的长是 。

5．直角三角形两边长分别为5和4，则它第三边为6.如图，所有的四边形都是正方形，所有的三角形 都是直角三角形，其中最大的正方形的边长为则正方形A ，B ，C ，D 的面积之和为___________cm 27.已知实数x 、y 满足|y －3|＋x －4＝0， 则8.平行四边形ABCD 的周长是56cm ，对角线AC 、BD 相交于点O ，△OAB 与△OBC 的周长差是4cm ，则平行四边形ABCD 中较短的边长是 。

9.已知菱形的两对角线长分别为6和8，则菱形的边长为________ 。

10.比较大小：32。

78.二、选择题（每题3分，共30分） 11. 16的算术平方根是（ ）A ．4B ．–4C ．2D ．±4 12. 下列计算正确的是（ ）A ．632=⨯B ．532=+C ．248=D ．224=-13.三角形的三边长为()ab c b a 222+=+,则这个三角形是 ( )A.等边三角形;B.钝角三角形;C.直角三角形;D.锐角三角形. 14. 一个正数的平方根为m -2与12+m ,则m 的值为 ( )A ． 31B ． 31或3- C ． 3- D ． 315．如果梯子的底端离建筑物9米，那么15米长的梯子可以达到建筑物的高度为（ ）A 10米B 11米C 12米D 13米16.矩形具有而平行四边形不具有的性质是 （ ）A 、对角线互相平分B 、两组对边分别相等C 、 对角线相等D 、相邻两角互补17. 如图，等边ΔABC 中，D 为BC 上一点, ΔABD 经过旋转后到达ΔACE的位置,如果∠BAD=18°,则旋转角等于（ ） A 、18° B 、 32° C 、60° D 、72°（第17题图）18. 以下列各组数据为边长作三角形，其中能组成直角三角形的是 （ ）A 、3、5、3B 、4、6、8C 、7、24、25D 、6、12、13 19.如图，延长正方形ABCD 的一边BC 至E ，使CE ＝AC ，连结AE 交CD 于F ，则∠AFC 的度数是（ ）A 、112.5°B 、120°C 、122.5°D 、135°20. 如右上图一只蚂蚁从长宽都是3，高是8的长方体纸箱的A 点沿纸箱爬到B 点，那么它所行的最短路线的长是( )A. (32+8)cm;B.10cm;C. 14cm;D.无法确定三、计算题（每题4分，共16分）21. 22. 23.班别姓名：学号：密封线内不要 答题AD F ECB（第19题图）24.32218-+四、作图题（每题4分，共12分） 25、如图，平移方格纸中的图形，使点A 平移 到点A ＇处，画出平移后的图形。

（第3题）实验中学2010学年度初二级第一学期期中考数学科试卷1、本试卷满分120分，另附附加题30分以20%计入总分,但全卷总分不得超过120分，考试时间90分钟。

2、请用蓝色或黑色钢笔或圆珠笔作答。

一、填空题（每空3分，共30分）1、如图，已知AC ＝DB ，要使△ABC ≌△DCB ，则需要补充的条件为_________________ 。

（一个即可）2、若一个等腰三角形有一个内角为20o，则另两个角分别为 。

3、如图，在平面镜里看到背后墙上,电子钟示数如图所示， 这时的实际时间应该是___ ___。

12cm ABC AB AC BC D E ADE BC 4、如图，中，、的垂直平分线交于点、，已知的周长为，则＝_____。

5、点P （1，2）关于y 轴对称的点的坐标是 。

06304cm _______Rt ABC CD B AD AB ∠==、中，是斜边上的高，，，则的长度是。

7、一灯塔P 在小岛A 的北偏西30°，从小岛A 沿正北方向前进20海里后到达小岛 B ，•此时测得灯塔P 在小岛B 北偏西60°方向，则P与小岛B 相距________．8、一个数的算术平方根是8，则这个数的立方根是__________。

9、比较大小：76。

10、_______x 的平方根为。

二、选择题（每题3分，共24分）姓 名学 校班 级学 号密 封 线 内 不 要 答 题（第1题）(第4题)ACCBDE11、在下列实数中，是无理数的为（）。

A、0B、 3.5-CD12、如图，某人把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，最省事的办法是。

( )A、带①去B、带②去C、带③去D、带①和②去13、__________线段有对称轴。

( )A、1条B、2条C、3条D、4条14、下列三角形不一定全等的是（）A、面积相等的两个三角形B、周长相等的两个等边三角形C、斜边和一条直角边分别对应相等的两个直角三角形D、有一个角是100°，腰长相等的两个等腰三角形15、16的算术平方根为（）A、4B、4±C、2 D、2±16、 1.844 5.830______≈≈≈。

河南省实验中学八年级数学上册期中试题一、选择题1. 下列运算正确的是（ ） A2=±B ．2142-⎛⎫=- ⎪⎝⎭C2=-D ．|2|2--=2. 在下列实数中，无理数是（ ） A ．13B ．πCD ．2273. 下列判断中错误．．的是（ ） A ．有两角和一边对应相等的两个三角形全等 B ．有两边和一角对应相等的两个三角形全等C ．有两边和其中一边上的中线对应相等的两个三角形全等D ．有一边对应相等的两个等边三角形全等4. 如图，点P 是∠BAC 的平分线AD 上一点，PE ⊥AC 于点E ． 已知PE =3，则点P 到AB 的距离是（ ）A ．3B ．4C ．5D ．6 5. 如图，已知：AB ∥EF ，CE =CA ，∠E =65，则 ∠CAB 的度数为A.25 B.50 C.60 D.656. 已知一个等腰三角形两内角的度数之比为1:4，则这个等腰三角形顶角的度数为（ ） A ．20B ．120C ．20或120D ．36二、填空题7. 右图是用七巧板拼成的一艘帆船，其中全等的三角形共有 对．8. 如图，线段AC 与BD 交于点O ，且OA=OC, 请添加一个条件，使△OAB ≅△OCD, 这个条件是______________________.9. 如图，AC 、BD 相交于点O ，∠A ＝∠D ，请你再补充一个条件，使得△AOB ≌△DOC ， 你补充的条件是 ．10. 如图，50ABC AD ∠=，垂直平分线段BC 于点D ABC ∠，的平分线BE 交AD 于 点E ，连结EC ，则AEC ∠的度数是 ．11. 夷陵长江大桥为三塔斜拉桥．如图，中塔左右两边所挂的最长钢索AB AC =，塔柱底端D 与点B 间的距离是228米，则BC 的长是 米．12. 如图，在ABC △中，点D 是BC 上一点，80BAD ∠=°，AB AD DC ==，则C ∠= 度．13. 已知Rt ABC △中，90C =∠，6AC =，8BC =，将它的一个锐角翻折，使该锐角顶点落在其对边的中点D 处，折痕交另一直角边于E ，交斜边于F ，则CDE △的周长为 ．14.如图，三角形纸片ABC ，10cm 7cm 6cm AB BC AC ===，，， 沿过点B 的直线折叠这个三角形，使顶点C 落在AB 边上的点E 处， 折痕为BD ，则AED △的周长为 cm ．15. 写出一个大于2的无理数 ．16. ABC △为等边三角形，D E F ，，分别在边BC CA AB ，，上，且AE CD BF ==，则DEF △为 三角形 三、计算题17. 计算20071(1)52+-+-四、画(作)图题18. 近年来，国家实施“村村通”工程和农村医疗卫生改革，某县计划在张村、李村之间建一座定点医疗站P ，张、李两村座落在两相交公路内(如图所示)．医疗站必须满足下列条件：①使其到两公路距离相等，②到张、李两村的距离也相等，请你通过作图确定P 点的位置．五、证明题ABCDACBD80CD19. 已知：如图，OP 是AOC ∠和BOD ∠的平分线，OA OC OB OD ==，． 求证：AB CD =．20. 已知：如图，直线AD 与BC 交于点O ，OA OD =，OB OC =． 求证：AB CD ∥．21. 如图，在等腰R t △ABC 中，∠ACB =90°，D 为BC 的中点，DE ⊥AB ，垂足为E ， 过点B 作BF ∥AC 交DE 的延长线于点F ，连接CF ． (1)求证：AD ⊥CF ；(2)连接AF ，试判断△ACF 的形状，并说明理由．22. 如图，在等边ABC △中，点D E ，分别在边BC AB ，上，且BD AE =，AD 与CE 交于点F ．（1）求证：AD CE =； （2）求DFC ∠的度数．七、开放题B AC O DPA B DC O23. 如图，D E ，分别为ABC △的边AB AC ，上的点，BE 与CD 相交于O 点．现有四个条件：①AB AC =，②OB OC =，③ABE ACD ∠=∠，④BE CD =． （1）请你选出两个条件作为题设，余下的两个作为结论，写出一个正确．．的命题： 命题的条件是 和 ，命题的结论是 和（均填序号）．（2）证明你写出的命题． 已知： 求证： 证明：八、猜想、探究题24. 已知四边形ABCD 中，AB AD ⊥，BC CD ⊥，AB BC =，120ABC =∠，60MBN =∠，MBN ∠绕B 点旋转，它的两边分别交AD DC ，（或它们的延长线）于E F ，．当MBN ∠绕B 点旋转到AE CF =时（如图1），易证AE CF EF +=．当MBN ∠绕B 点旋转到AE CF ≠时，在图2和图3这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，线段AE CF ，，EF 又有怎样的数量关系？请写出你的猜想，不需证明．参考答案B C（图1） A B CD E FMN （图2）AB CDE FMN（图3）AB C DE F MN一、选择题1. Ｃ2. B3. B4. A5. B6. C 二、填空题7. 2 8. ∠A =∠C ,∠B =∠D ，OD =OB AB ∥CD9. AO ＝DO 或AB ＝DC 或BO ＝CO10.115°（填115不扣分） 11. 45612. 25 13. 10或11 14. 9 15.16. 正 三、计算题 17. 解： 原式=21-1+21-5（后面三个数中每计算正确一个得2分）4分= 1-1-5 = -56分四、证明题 18. 画(作)图题画出角平分线 3分 作出垂直平分线 3分19. 证明：因为OP 是AOC ∠和BOD ∠的平分线， 所以 A O P C O P ∠=∠，BOP DOP ∠=∠． 所以AOB COD ∠=∠． 在AOB △和COD △中，OA OC AOB COD OB OD =⎧⎪∠=∠⎨⎪=⎩，，， 所以AOB COD △≌△． 所以 AB CD =．20. 在AOB △和DOC △中，OA OD =，OB OC =，又AOB DOC =∠∠， AOB DOC ∴△≌△， 3分 A D ∴=∠∠， 4分 AB CD ∴∥．6分21. (1)证明：在等腰直角三角形ABC 中，∵∠ACB =90o ，∴∠CBA =∠CAB =45°． 又∵DE ⊥AB ，∴∠DEB =90°，∴∠BDE =45°． 又∵BF ∥AC ，∴∠CBF =90°， ∴∠BFD =45°=∠BDE ， ∴BF =DB ．…………2分 又∵D 为BC 的中点，∴CD =DB ，即BF =CD ． 在R t △CBF 和R t △ACD 中，⎪⎩⎪⎨⎧==∠=∠=︒,,90,AC CB ACD CBF CD BF ∴R t △CBF ≌R t △ACD ，∴∠BCF =∠CAD ． ……………………………………………………………4分 又∵∠BCF +∠GCA =90°， ∴∠CAD +∠GCA =90°，即AD ⊥CF ；……………………………………………6分 (2) △ACF 是等腰三角形．理由：由(1)知： CF =AD ，△DBF 是等腰直角三角形，且BE 是∠DBF 的平分线， ∴BE 垂直平分DF ，即AF =AD ，…………………………………………………8分 ∴CF =AF ，∴△ACF 是等腰三角形． ………………………………………………………10分22. （1）证明：ABC △是等边三角形，60BAC B ∴==∠∠，AB AC =又AE BD =(SAS)AEC BDA ∴△≌△，4分 AD CE ∴=．5分 （2）解由（1）AEC BDA △≌△， 得ACE BAD =∠∠6分DFC FAC ACE ∴=+∠∠∠60FAC BAD =+=∠∠ 8分七、开放题 23. 解：（1）①，③；②，④．（注：①④为题设，②③为结论的命题不给分， 其他组合构成的命题均给4分）（2）已知：D E ，分别为ABC △的边AB ，AC 上的点， 且AB AC =，ABE ACD ∠=∠．求证：OB OC BE CD ==，． 4分证明：AB AC =，ABE ACD ∠=∠， ABC ACB ∴∠=∠，且ABE ACD △≌△． BE CD ∴=． 6分又BCD ACB ACD ABC ABE CBE ∠=∠-∠=∠-∠=∠， BOC ∴△是等腰三角形．OB OC ∴=． 8分八、猜想、探究题24. 图2成立，图3不成立． 2分证明图2．延长DC 至点K ，使CK AE =，连结BK ，B CAB C D E FMNK则BAE BCK △≌△，∴BE BK ABE KBC =∠=∠，，60FBE ∠=，120ABC ∠=， ∴60FBC ABE ∠+∠=，60FBC KBC ∴∠+∠=， 60KBF FBE ∴∠=∠=， ∴KBF EBF △≌△， ∴KF EF =，∴KC CF EF +=， 即AE CF EF +=．6分图3不成立，AE CF EF ，，的关系是AE CF EF -=． 8分。

河南省实验中学2011--2012学年下期期中试卷八年级 数学（时间：100分钟， 满分120分）一、选择题（每小题3分，共24分） 1.如果b a >，下列各式中不正确的是………………………………………………………【 】（A ）22b a > （B ）b a 22-<- （C ）33->-b a （D ）ba 11< 2．把多项式332223224168bc a cb a b a -+-分解因式，应提的公因式是……………………【 】（A ）bc a 28- （B ）3222c b a （C ）abc 4- （D ）33324c b a3．把()223)(6x y y y x ----分解因式，结果是………………………………………………【 】 （A ）()2)(32+-y y x (B) ()y y x 36)(2--- (C) ()y y x +--2)(32 (D) ()2)(32--y y x4．如果不等式组⎩⎨⎧><mx x 8有解，那么m 的取值范围是………………………………………【 】 （A ） 8>m （B ） 8<m （C ） 8≥m （D ）8≤m 5.若分式392--x x 的值为0，则x 的值为…………………………………………………………【 】 （A ） 3 （B ） 33-或 （C ） 3- （D ）0（A ）00002315<<x （B ）00003515<<x （C ）00004723<<x （D ）00005023<<x7.关于x 的方程xx x a --=+-2132有增根，则a 的值为…………………………………………【 】 （A ） 1 （B ）2 （C ） 1- （D ）3 8.已知ABC ∆与C B A '''∆的相似比为32，C B A '''∆与C B A '''''''∆的相似比为45，则A B C ∆与C B A '''''''∆的相似比为…………………………………………………………………………………………【 】（A ）65 （B ）56 （C）65或56 （D ）158二、填空题（每小题3分，共27分）9.已知关于x 的方程102=-a x 的解不大于3，则a 的取值范围为 ．10. 分解因式：=-a a 1232 ．11.若92++mx x 是一个完全平方式，则=m ．12.已知21=+a a ，则=+221a a ． 13.如果1)1(13-+=--x B x A x x x ，则实数=A ,=B ． 14.若))(3(152n x x mx x ++=-+，则=m ．15.若ab b a 2=-，则=-ba 11 ． 16. 线段cm AB 10=,点P 和点Q 是线段AB 的两个黄金分割点，则=PQ cm ．17．若关于x 的不等式组⎩⎨⎧>-<-3212b x a x 的解集为11<<-x ，则)1)(1(-+b a 的值为 ． 三、解答题 （本大题共6小题，共69分）18．（本题满分8分）解不等式组⎪⎩⎪⎨⎧++≤+-<+②① (13212)1...........................313x x x x ，并写出它的所有整数解．19.（本题满分8分） 1232-可以被10和20之间的某两个整数整除，求这两个数.20. 化简求值（每小题9分，共18分）（1）先化简22144(1)11x x x x -+-÷--，然后从－2≤x ≤2的范围内选取一个合适的整数作为x 的值代入求值.（2）若m a 111-=，1211a a -=，2311a a -=，…；求2011a 的值.（用含m 的代数式表示）21.（本题满分11分）某校志愿者团队在重阳节购买了一批牛奶到“夕阳红”敬老院慰问孤寡老人，如果给每个老人分5盒，则剩下38盒，如果给每个老人分6盒，则最后一个老人不足5盒，但至少分得1盒.（1）设敬老院有x名老人，则这批牛奶共有多少盒？（用含x的代数式表示）（2）该敬老院至少有多少名老人？最多有多少名老人？22.（本题满分12分）甲、乙两人准备整理一批新到的实验器材，若甲单独整理需要40分钟完工；若甲、乙共同整理20分钟后，乙再单独整理20分钟才能完工.（1）问乙单独整理多少分钟完工？（2）若乙因工作需要，他的整理时间不超过30分钟，则甲至少整理多少分钟才能完工？23.（本题满分12分）某高新科技公司根据市场需要，计划生产A、B两种型号的医疗器械.其部分信息如下：信息一：A、B两种型号的医疔器械共生产80台．信息二：该公司所筹生产医疗器械资金不少于1800万元，但不超过1810万元．且把所筹资金全部用于生产此两种医疗器械．根据上述信息，解答下列问题：（1）该公司对此两种医疗器械有哪几种生产方案？哪种生产方案能获得最大利润？（2）根据市场调查，每台A型医疗器械的售价将会提高a万元)0(a．每台B型医疗器械的售价不会改变，该公司应该如何生产可以获得最大利润？（注：利润=售价－成本）参考答案二、填空题（每小题3分，共27分）18.解：解不等式①得：2-<x ，…………………………………………………………………2分 解不等式②得：5-≥x ，…………………………………………………………………4分 所以，原不等式组的解集为：25-<≤-x .…………………………………………………6分所以，不等式组的所有整数解为：345---=、、x .…………………………………………8分 19.解：1232-22161)2(-=)12)(12(1616-+=…………………………………………………………………2分)12)(12)(12(8816-++=)12)(12)(12)(12(44816-+++=………………………………………………………4分)116()116()12)(12(816-⨯+⨯++=1517)12)(12(816⨯⨯++=.……………………………………………………………6分所以，1232-可以被17和15两个整数整除. …………………………………………………8分20.（1）解：原式＝22(1)(1)1(2)x x x x x -+-∙--……………………………………………………………3分 ＝12x x +-.…………………………………………………………………………………5分 因为，x 满足－2≤x ≤2且为整数，所以，若使分式有意义，x 只能取0，－2.…………………………………………………7分当0=x 时，原式＝12-. （或：当x ＝－2时，原式＝14）. …………………………………………………………………9分（2）解：因为，m a 111-=m m mm m 11-=-=； 1211a a -=mm 111--=11--=m m 111----=m m m m 11---=m m m 11--=m 11--=m ； 2311a a -=1111---=m m m =-+=11；…………………………………………………3分 3411a a -=m 11-=m m m m m 11-=-=； 4511a a -=m m 111--=11--=m m 111----=m m m m 11---=m m m 11--=m 11--=m ； …因此，3个一循环，又因为2011÷3=670……1，所以2011a 与1a 的值相同.所以2011a mm m 111-=-=.……………………………………………………………………9分 21.解：（1）这批牛奶共有)385(+x 盒；……………………………………………………………3分（2）设敬老院有x 名老人，则这批牛奶共有)385(+x 盒，根据题意，得：⎩⎨⎧≥--+<--+1)1(6)385(5)1(6)385(x x x x . ……………………………………………………………………7分 解这个不等式组得：4339≤<x . ………………………………………………………………………………9分 因为x 只能为正整数，所以，43424140或或或=x .所以，该敬老院至少有40名老人，最多有43名老人. …………………………………………………11分22.解：（1）设乙单独整理x 分钟完工. 根据题意，得：120204020=++x.…………………………………………………………………5分 解得：80=x .经检验：80=x 是所列分式方程的解. …………………………………………7分 答：乙单独整理80分钟完工.（2）设甲整理m 分钟完工， 根据题意，得：1408030≥+m .………………………………………………………………………10分 解这个不等式，得;25≥m .答：甲至少要整理25分钟才能完工. …………………………12分23.解：（1）设该公司生产A 型器械x 台，则生产B 型器械)80(x -台，根据题意，得：⎩⎨⎧≤-+≥-+1810)80(25201800)80(2520x x x x . …………………………………………………………………………4分 解这个不等式组得：4038≤≤x .因为，x 取正整数，所以，403938或或=x .所以，该公司有3种生产方案：方案一：生产A 型38台，B 型42台；方案二：生产A 型39台，B 型41台；方案一：生产A 型40台，B 型40台. …………………………………………………………6分 设该公司生产A 型x 台，公司获得利润为W （万元），则400)80)(2530()2024(+-=--+-=x x x W .因为，01<-=k ， 所以，W 随着x 的增大而减小.所以，当38=x 时， W 有最大值.∴当生产A 型器械38台，B 型器械42台时获得最大利润. ……………………………………8分（2）仍然设该公司生产A 型器械x 台，公司获得利润为W （万元），根据题意，得，400)1()80)(2530()2024(+-=--+-+=x a x x a W ………………………………………………………9分 因为，)1(-=a k ，情况不明确，不得不分类讨论如下：①当01>-a ，即1>a 时，W 随着x 的增大而增大.生产A 型40台，B 型40台，获得最大利润； ②当01=-a ，即1=a 时，（1）中三种方案利润都为400万元；③当01<-a ，即10<<a 时，W 随着x 的增大而减小.生产A 型38台，B 型42台，获得最大利润. …………………………………………………………………………………………………………………12分。

河南省实验中学⼋年级下期中数学试卷及答案好资料学习-----学年下期期中试卷河南省实验中学20172016——分）（时间：100分钟，满分：12010⼩题，每⼩题3分，共30分）⼀、选择题：（本⼤题共nm，下列不等式不⼀定成⽴的是（．若1）＞nm22mmmnnCn．＞ A．．+3＞．+3 B3 D＞3＞22 2．下列说法正确的是（）．平移不改变图形的形状和⼤⼩，⽽旋转则改变图形的形状和⼤⼩ A．在成中⼼对称的两个图形中，连结对称点的线段都被对称中⼼平分 B个单位，纵坐标加2．在平⾯直⾓坐标系中，⼀点向右平移 C2 D．在平移和旋转图形中，对应⾓相等，对应线段相等且平⾏．下列命题：3①有⼀个⾓为 60°的等腰三⾓形是等边三⾓形；453的三⾓形为直⾓三⾓形；②三边长为，，或8；，则等腰三⾓形的周长为③等腰三⾓形的两条边长为 2，410④到线段两端距离相等的点在这条线段的垂直平分线上．）正确的个数有（． D1个．．． A4个 B3个 C2个（三点CB4．⼀只花猫发现⼀只⽼⿏溜进了⼀个内部连通的洞，⿏洞只有三个出⼝A、、不在同⼀直线上），要想同时顾及这三个出⼝以防⽼⿏出洞，这只花猫最好蹲守在（） ABC A．△三条⾼线的交点处三条⾓平分线的交点处 B．△ABC C．△三边中线的交点处ABC ．△ABC三边垂直平分线的交点处 D 已知点5.Pm）在第⼆象限，则﹣m，﹣3（m1 的取值范围在数轴上表⽰正确的是（）更多精品⽂档．学习-----好资料A. B. C.D. ）．下列四个等式从左到右的变形，是多项式因式分解的是（ 6??25x?x?1x?x?5?． A． B2?33aa?9?a?1222bab?aab?ab??x?xx?x． C. D??x??上确定⼀点P，使AC＜BC），⽤尺规在BC（7．如图，已知△ABC ）PA+PC=BC．则下列四种不同⽅法的作图中准确的是（．将正⽅形对折后展开（图④是连续两次对折后再展开），再按图⽰⽅法折叠，能够得8（）图①～④中这样的图形有到⼀个直⾓三⾓形，且它的⼀条直⾓边等于斜边的⼀半．个、2个 D、1 C B A、4个、3个O OA上有⼀动点，且，∠9．如图，∠AOB=30AOB内有⼀定点POP=10.在）PQR周长最⼩，则最⼩周长是（ΔR.OBQ，上有⼀动点若10 B A．．20 D.2515 C．更多精品⽂档．-----好资料学习 BC中点．∠MDN=90°，AB=AC=2，点D10．Rt△ABC中，为两点．交于E、F旋转，DM、DN分别与边AB、ACD∠MDN绕点S≤S下列结论：①（=BC；②BE+CF）；△ABC△AEF A到线段EF的距离最③S=AD?EF；④AD≥EF；⑤点AEDF四边形1，其中正确结论的个数是（）⼤为 3 D、4、A、1 B2 C、分，共15分）⼆、填空题（本⼤题共5⼩题，每⼩题32xyyx=_____________________. ）－（－）分解因式（11.－1a?2x??)?3(a?3)(b1?1?? x_______.的值等于若不等式组，则的解集为12.?3b?x?2?，⼀腰上的中线把三⾓形的周长分为两部分，其中10cm13.已知等腰三⾓形的底边长为．⼀部分⽐另⼀部分长5cm，那么这个三⾓形的腰长为_____cm吨，⼄546吨货物运往A地，甲种运输车载重某物流公司现⽤甲、⼄两种运输车将14. 辆．辆，则甲种运输车⾄少应安排吨，安排车辆不超过10种运输车载重4OC的位置，点B、15．如图，在平⾯直⾓坐标系中，将△ABO绕点A顺时针旋转到△AB11的位置，BC顺时针旋转到△轴上，再将△ABC绕点BAx、分别落在点BC处，点B在211111111轴上，依次进AC的位置，点在x顺时针旋转到△B点C在x轴上，将△AC绕点CAB22222121232，），则点B的坐标为． B ⾏下去…．若点A（，0），（02017275题，共分）三、解答题（本⼤题共82?5x?x1—?16.，并将解集在数轴上表⽰出来．分）解不等式：（本题6 23更多精品⽂档．好资料学习-----xky≤1，若存在，，使⽅程组＞1，17．（本题8分）是否存在整数的解满⾜k求出的值，若不存在，说明理由．b?y?kx A中，⼀次函数的图象经过点18.（本题9分）如图，在平⾯直⾓坐标系xOy2x?y?24?2 ，）．（（的图象交于点B，），且与正⽐例函数a3的值；（1）求a 2的解集；2（）写出不等式kx+b＞b?y?kx的图象与（3）若⼀次函数x 轴交于点C，且正⽐例2x?y?函数）个单位长度后经过点（m>0的图象向下平移m 3 的值；C，求m2bkx?-x?的不等式）直接写出关于（4x的解集．3，⊥ACDE⊥AB，DFD919.（本题分）如图，∠BAC的平分线与BC的垂直平分线相交于点，的长．，AB=6AC=3，求BE垂⾜分别为E、F，，连结BC上，AE=ADBAC=90°，AB=AC，点D在底边中，∠分）在20.（本题10Rt△ABC0°BAD=6时，求∠CDE的度数；．（DE1）当∠B（点、C除外）上运动时，试猜BC D2（）当点在的数量关系；CDEBAD想并探究∠与∠更多精品⽂档．学习-----好资料21.（本题10分）某市现有两种⽤电收费⽅法：分时电表普通电表峰时（8：00—21：00）⾕时（21：00到次⽇8：00）电价0.56元/度/度电价0.36元电价0.60元/度⼩明家所在的⼩区的电表都换成了分时电表，根据情况回答下列问题：（1）第⼀季度⼩明家⽤电情况为：⾕时⽤电量100度，峰时⽤电量300度，这个季度的费⽤和⽤普通电表收费相⽐，哪种收费⽅法合算？试说明理由.（2）⼀⽉份⼩明家⽤电120度，那么⼩明家使⽤分时电表是不是⼀定⽐普通电表合算？试说明理由.22．在中，AB=20cm，BC=16cm，点D为线段AB的中点，ABC 分）（本题11动点P以2cm/s的速度从B点出发在射线BC上运动，同时点Q以a cm/s（a＞0且a．．秒．xC点出发在线段CA上运动，设运动时间为2≠）的速度从全等？BPD和△CQPBC，P在线段上，求当a为何值时，能够使△AB=AC（1）若060??BBDP?，求出发⼏秒后，）若（2为直⾓三⾓形？070??CCPQ?CPQ?的度数为多少时，，当3（）若为等腰三⾓形？（请直接写出答案，不必写出过程）．更多精品⽂档．学习-----好资料23．（本题12分）阅读下⾯材料，并解决问题：ABCPPABC的距离分别为3，4内有⼀点、，若点，到顶点5、，）如图①等边△（1APB的度数．求∠ABPAACPACPABP，旋转到△′≌△为了解决本题，我们可以将△′处，此时△绕顶点PAPBPC转化到⼀个三⾓形中，从⽽求出∠这样就可以利⽤旋转变换，将三条线段、、APB= ；（2）基本运⽤请你利⽤第（1）题的解答思想⽅法，解答下⾯问题ABCCABABACEFBCEAF=45°，、已知如图②，△上的点且∠中，∠°，=90为=求证：，222FCBEEF； =+（3）能⼒提升RtABCCACABCORtABC内⼀点，连接为=1，∠=30如图③，在°，点△中，∠°，=90△AOBOCOAOCCOBBOAOAOBOC的值．+=120°，求+ ∠，，，且∠=∠=更多精品⽂档学习-----好资料河南省实验中学学年下期期中试卷答2016-2017案（时间：100分钟，满分：120分）⼀、选择题：（本⼤题共10⼩题，每⼩题3分，共30分）5 D B C D A— 16—10 D D C A C⼆、填空题（本⼤题共5⼩题，每⼩题3分，共15分）15 14. -2 13. 6 15. y-x）（y-x-1） 12. 11. （），0（6062 75分）三、解答题（本⼤题共8题，共 16、解不等式：2??5xx1?—23<6 x+2）（ 2（x+5）-3 解 2x+10-3x-6<6-x<2） x>-2 图象（略解：解⽅程组17解得yx≤1∵＞1，更多精品⽂档．好资料学习-----k5 ≤解之得2＜k⼜∵为整数k5，只能取3，4∴yxk 1，4，5。

河南省实验中学2023-2024学年上期期中考试（时间:120分钟，满分:150分）一、单项选择题:本题共8小题，每小题5分，共40分.在每小题给出的4个选项中，只有一个选项是符合题目要求的高三数学试题.，则R ()A B =（．[[2,3]−1,0] ．已知单位向量a 与单位向量b 的夹角为，则2a b −=（3．−+x y x y (3)25)(的展开式中，x y 33的系数为（ ） A ．200B ．40C ．120D ．80．已知一个圆锥的侧面展开图是一个圆心角为120的扇形，若该圆锥底面圆的半径4AP AQ a =−2，则双曲线二、多项选择题:本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得0分. 9．设i 为虚数单位，下列关于复数的命题正确的有（ ）10．已知>>a b 0,0，且+=a b ab 则（ ）2,2⎤⎡+∞⎦⎣2π对称 两点，且=AB 两点，则下列说法中正确的是（ ）三、填空题:本题共4小题，每小题5分，共20分.13．数列a n {}的前n 项和为S n ，若=a 21，=+a S n n 31(∈+n N )，则=a 4 14．若将5名志愿者安排到三个学校进行志愿服务，每人只去一个学校，每个学校至 少去一人，则不同的分配方案共有 种.（用数字作答）15．在三棱锥P ABC −中，∆ABC 是边长为2的等边三角形，⊥PA 平面ABC ，若P ，A B C ,,四点都在表面积为π16的球的球面上，则三棱锥P ABC −的体积为 .16．设=−++∈f x x a e x a a R x ()(),，则下列说法正确的是 .①=f (0)0； ②若f x ()在定义域内单调，则≤a 2； ③若=a 0，则−>f x x ex ()2ln 恒成立； ④若>a 2，则f x ()的所有零点之和为0. 四、解答题:本题共6小题，共70分.解答应写出必要的文字说明、证明过程或演算骤. ，求ABC 的周长．，记(1)n n n S a a a a a −=−+−++−12341为数列参考答案：）在ABC 中，因为)(A B a +=)(a c a −=0πB <<，故，所以ABC 的周长为N +∈时，2231(1)37(12)2n n n −+−++−−=−−++−=时，22149162n n n S n +=−+−++=；,221n k n k ==−()k N +∈（或n S =21(1)2n n n −+−）在PAD 中，PAC △中，ACAD A =，BD ⊂平面ABCD AC PA A ⋂=，⊂平面PAC ）记AC BD O =，连接PA ，又由（1）知O 为坐标原点，OB 图所示，所以(BP =−，(BA =−的一个法向量为(111,n x y =1100n BP n BA ⎧⋅=⎪⎨⋅=⎪⎩，即111133x y x y −+−=0=，所以平面BAP 的一个法向量为(11,n =−E 是PC 的中点，且()0,2,2PC =−，所以(1122PE PC ==⨯所以()()3,1,20,1,3,0,1BE BP PE =+=−−+−，又(2BD =−设平面BDE 的一个法向量为(222,n x y =220022300202121212cos ,2n n n n n n ⋅−==⨯⋅023=p 【详解】()2436C 412p p ⎡=−−⎣20,⎫时，()0f p '>，综上a 的取值范围为[1ln 2,1ln 2)e e−−−−.。

2019-2020学年八年级上学期期中考试数学试题一、选择题（每小题3分，共30分）1.下列图形中是轴对称图形的有（）A.1个B.2个C.3个D.4个【答案】B【解析】第一个图形不是轴对称图形，第二个图形是轴对称图形，第三个图形不是轴对称图形，第四个图形是轴对称图形，因此是轴对称图形的有2个，故选B.2.如图，为估计池塘岸边A、B的距离，小方在池塘的一侧选取一点O，测得OA＝15米，OB＝10米，A、B间的距离不可能是()A.20米B.15米C.10米D.5米【答案】D【解析】∵5<AB<25，∴A、B间的距离不可能是5，故选D.3.如图，把一副含30°角和45°角的直角三角板拼在一起，那么图中∠ADE是（）A.100°B.120°C.135°D.150°【答案】C【解析】因为∠ADE是△DEB的外角,所以∠ADE=∠DEB+∠EBD=45°+90°=135°,故选C.4.尺规作图作AOB的平分线方法如下：以O为圆心，任意长为半径画弧交OA、OB于C、D，再分别以点C、D为圆心，以大于12CD长为半径画弧，两弧交于点P，作射线OP，由作法得OCP ODP≌的根据是（）A.SASB.ASAC.AASD.SSS【答案】D【解析】解：以O为圆心，任意长为半径画弧交OA，OB于C，D，即OC=OD；以点C，D为圆心，以大于CD长为半径画弧，两弧交于点P，即CP=DP；再有公共边OP，根据“SSS”即得△OCP≌△ODP．故选D．5.已知点P（-6，3）关于x轴的对称点Q的坐标（a，b），则M(-a，b)在（）A.第一象限B.第二象限C.第三象限D.第四象限【答案】D【解析】∵点P（-6，3）关于x轴的对称点Q的坐标（a，b），∴a=-6，b=-3，∴M（-a,b）为M（6，-3），在第四象限，故选D.6.如图，在△ABC与△DEF中，给出以下六个条件：①AB=DE；②BC=EF；③AC=DF；④∠A=∠D；⑤∠B=∠E；⑥∠C=∠F，以其中三个作为已知条件，不能判断△ABC与△DEF全等的是（）A.①②⑤B.①②③C.①④⑥D.②③④【答案】D【解析】在A选项中，根据SAS可证明△ABC≌△DEF；在B选项中，根据SSS可证明△ABC≌△DEF；在C选项中，根据AAS可证明△ABC≌△DEF；在D选项中，只满足SSA，而SSA不能判定两个三角形全等，所以以D选项中的三个已知条件，不能判定△ABC和△DEF全等，故选D．7.如图，AB⊥BC，BE⊥AC，∠1=∠2，AD=AB，则（）A.∠1=∠EFDB.BE=ECC.BF=DF=CDD.FD∥BC【答案】D【解析】由SAS易证△ADF≌△ABF，根据全等三角形的对应边相等得出∠ADF=∠ABF，又由同角的余角相等得出∠ABF=∠C，则∠ADF=∠C，根据同位角相等，两直线平行，得出FD∥BC．解：在△ADF与△ABF中，∵AF=AF，∠1=∠2，AD=AB，∴△ADF≌△ABF，∴∠ADF=∠ABF，又∵∠ABF=∠C=90°-∠CBF，∴∠ADF=∠C，∴FD∥BC．故选B．8.已知等腰三角形的周长为24，其中两边之差为6，则这个等腰三角形的腰长为（）A.10B.6C.4或6D.6或10【答案】A【解析】设腰长为a，则底边长为a+6或a-6，若底边长为a+6，则有2a+a+6=24，a=6，此时底边长为12，6+6=12，构不成三角形；若底边长为a-6，则有2a+a-6=24，a=10，综上，所以三角形的腰长为10，故选A.9.如图，在正方形网格中，网格线的交点称为格点．已知A，B是两格点，若点C也是图中的格点，且使得△ABC为等腰三角形，则符合题意的点C有（）A.6个B.7个C.8个D.9个【答案】C【解析】试题分析：如图：分情况讨论①AB为等腰△ABC底边时，符合条件的C点有2个；②AB为等腰△ABC其中的一条腰时，符合条件的C点有4个．故选A．考点：1.等腰直角三角形；2.勾股定理．【此处有视频，请去附件查看】10.如图，每个小方格都是边长为1的小正方形，△ABC是格点三角形(即顶点恰好是小正方形的顶点)，在图中与△ABC全等且有一条公共边的所有格点三角形的个数是()A.5B.4C.3D.2【答案】B【解析】考点：全等三角形的判定。