江苏大学高等代数2009真题
- 格式:pdf
- 大小:46.97 KB
- 文档页数:2

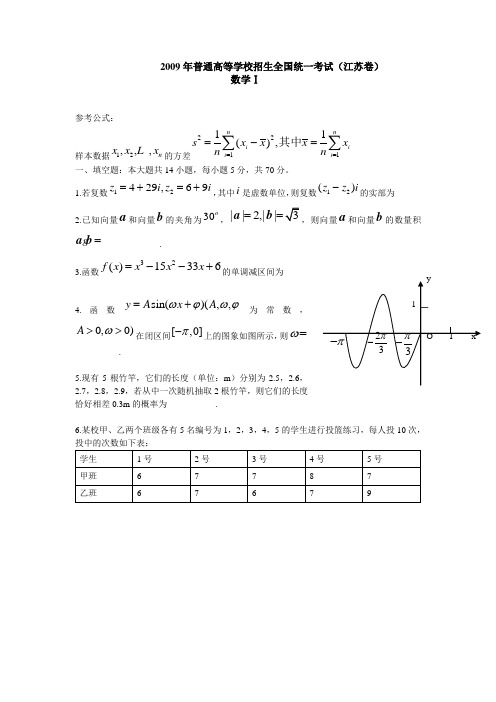
2009年普通高等学校招生全国统一考试(江苏卷)数学Ⅰ参考公式:样本数据12,,,n x x x 的方差221111(),n n i ii i s x x x x n n ===-=∑∑其中一、填空题:本大题共14小题,每小题5分,共70分。
1.若复数12429,69z i z i =+=+,其中i 是虚数单位,则复数12()z z i -的实部为______ 2.已知向量a 和向量b 的夹角为30,||2,||3==a b ,则向量a 和向量b 的数量积=a b __________ .3.函数32()15336f x x x x =--+的单调减区间为_____4.函数s i n ()(y A x A ωϕωϕ=+为常数,0,0)A ω>>在闭区间[,0]π-上的图象如图所示,则ω=_______ .5.现有5根竹竿,它们的长度(单位:m )分别为2.5,2.6,2.7,2.8,2.9,若从中一次随机抽取2根竹竿,则它们的长度恰好相差0.3m 的概率为________ .6.某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如下表: 学生 1号 2号 3号 4号 5号 甲班 6 7 7 8 7 乙班6767911 π-23π-3π-Oxy则以上两组数据的方差中较小的一个为2s=________ .7.右图是一个算法的流程图,最后输出的W=________ .8.在平面上,若两个正三角形的边长的比为1:2,则它们的面积比为1:4,类似地,在空间,若两个正四面体的棱长的比为1:2,则它们的体积比为________ .9.在平面直角坐标系xoy 中,点P 在曲线3:103C y x x =-+上,且在第二象限内,已知曲线C 在点P 处的切线的斜率为2,则点P 的坐标为________.10.已知512a -=,函数()xf x a =,若实数,m n满足()()f m f n >,则,m n 的大小关系为 ________. 11.已知集合{}2|log 2A x x =≤,(,)B a =-∞,若A B ⊆则实数a 的取值范围是(,)c +∞,其中c =________ .12.设α和β为不重合的两个平面,给出下列命题:(1)若α内的两条相交直线分别平行于β内的两条直线,则α平行于β; (2)若α外一条直线l 与α内的一条直线平行,则l 和α平行;(3)设α和β相交于直线l ,若α内有一条直线垂直于l ,则α和β垂直; (4)直线l 与α垂直的充分必要条件是l 与α内的两条直线垂直. 上面命题中,真命题的序号________(写出所有真命题的序号). 13.如图,在平面直角坐标系xoy 中,1212,,,A A B B 为椭圆22221(0)x ya b a b +=>>的四个顶点,F 为其右焦点,直线12A B 与直线1B F 相交于点T ,线段OT 与椭圆的交点M恰为线段OT的中点,则该椭圆的离心率为________.xyA1 B2A2 OTM开始0S ← 1T ←2S T S ←-10S ≥2T T ←+W S T ←+输出W 结束YN14.设{}n a 是公比为q 的等比数列,||1q >,令1(1,2,)n n b a n =+=若数列{}n b 有连续四项在集合{}53,23,19,37,82--中,则6q = ________二、解答题:本大题共6小题,共计90分。

绝密★启用前2009年普通高等学校招生全国统一考试(江苏卷)数学(理科)参考公式:样本数据12,,,n x x x 的方差221111(),n n i i i i s x x x x n n ===-=∑∑其中一、填空题:本大题共14小题,每小题5分,共70分。
请把答案填写在答题卡相应的位置上.......... 1.若复数12429,69z i z i=+=+,其中i 是虚数单位,则复数12()z z i -的实部为★.【答案】20- 【解析】略2.已知向量a 和向量b 的夹角为30,||2,||==a b a 和向量b 的数量积= a b ★ .【答案】3 【解析】232== a b 。
3.函数32()15336f x x x x =--+的单调减区间为 ★ .【答案】(1,11)- 【解析】2()330333(11)(1)f x x x x x '=--=-+,由(11)(1)0x x -+<得单调减区间为(1,11)-。
4.函数sin()(,,y A x A ωϕωϕ=+为常数,0,0)A ω>>在闭区间[,0]π-上的图象如图所示,则ω= ★. 【答案】3 【解析】32T π=,23T π=,所以3ω=, 5.现有5根竹竿,它们的长度(单位:m )分别为2.5,2.6,2.7,2.8,2.9,若从中一次随机抽取2根竹竿,则它们的长度恰好相差0.3m 的概率为 ★ . 【答案】0.2 【解析】略6.某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如下表:则以上两组数据的方差中较小的一个为s =★ .【答案】25【解析】略7.右图是一个算法的流程图,最后输出的W = ★ .【答案】22 【解析】略8.在平面上,若两个正三角形的边长的比为1:2,则它们的面积比为1:4,类似地,在空间,若两个正四面体的棱长的比为1:2,则它们的体积比为 ★ . 【答案】1:8 【解析】略9.在平面直角坐标系xoy 中,点P 在曲线3:103C y x x =-+上,且在第二象限内,已知曲线C 在点P 处的切线的斜率为2,则点P 的坐标为 ★ . 【答案】(2,15)- 【解析】略 10.已知12a-=,函数()xf x a =,若实数,m n 满足()()f m f n >,则,m n 的大小关系为 ★ . 【答案】m n < 【解析】略 11.已知集合{}2|log 2A x x =≤,(,)B a =-∞,若A B ⊆则实数a 的取值范围是(,)c +∞,其中c =★ .【答案】4【解析】由2log 2x ≤得04x <≤,(0,4]A =;由A B ⊆知4a >,所以c =4。

2009年江苏省高考数学试卷一、填空题(共14小题,每小题5分,满分70分)1.(5分)若复数z1=4+29i,z2=6+9i,其中i是虚数单位,则复数(z1﹣z2)i的实部为.2.(5分)已知向量和向量的夹角为300,,则向量和向量的数量积=.3.(5分)函数f(x)=x3﹣15x2﹣33x+6的单调减区间为.4.(5分)函数y=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0)在闭区间[﹣π,0]的图象如图所示,则ω=.5.(5分)现有5根竹竿,它们的长度(单位:m)分别为2.5,2.6,2.7,2.8,2.9,若从中一次随机抽取2根竹竿,则它们的长度恰好相差0.3m的概率为.6.(5分)某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如表:学生1号2号3号4号5号甲班67787乙班67679则以上两组数据的方差中较小的一个为S2=.7.(5分)如图是一个算法的流程图,最后输出的W=.8.(5分)在平面上,若两个正三角形的边长的比为1:2,则它们的面积比为1:4,类似地,在空间内,若两个正四面体的棱长的比为1:2,则它们的体积比为.9.(5分)在平面直角坐标系xOy中,点P在曲线C:y=x3﹣10x+3上,且在第二象限内,已知曲线C在点P处的切线斜率为2,则点P的坐标为.10.(5分)已知,函数f(x)=log a x,若正实数m,n满足f(m)>f (n),则m,n的大小关系为.11.(5分)已知集合A={x|log2x≤2},B=(﹣∞,a),若A⊆B则实数a的取值范围是(c,+∞),其中c=.12.(5分)设α和β为不重合的两个平面,给出下列命题:(1)若α内的两条相交直线分别平行于β内的两条直线,则α平行于β;(2)若α外一条直线l与α内的一条直线平行,则l和α平行;(3)设α和β相交于直线l,若α内有一条直线垂直于l,则α和β垂直;(4)直线l与α垂直的充分必要条件是l与α内的两条直线垂直.上面命题,真命题的序号是(写出所有真命题的序号)13.(5分)如图,在平面直角坐标系xoy中,A1,A2,B1,B2为椭圆=1(a>b>0)的四个顶点,F为其右焦点,直线A1B2与直线B1F相交于点T,线段OT与椭圆的交点M恰为线段OT的中点,则该椭圆的离心率为.14.(5分)设{a n}是公比为q的等比数列,|q|>1,令b n=a n+1(n=1,2,…),若数列{b n}有连续四项在集合{﹣53,﹣23,19,37,82}中,则6q=.二、解答题(共6小题,满分90分)15.(14分)设向量(1)若与垂直,求tan(α+β)的值;(2)求的最大值;(3)若tanαtanβ=16,求证:∥.16.(14分)如图,在直三棱柱ABC﹣A1B1C1中,E,F分别是A1B,A1C的中点,点D在B1C1上,A1D⊥B1C.求证:(1)EF∥平面ABC;(2)平面A1FD⊥平面BB1C1C.17.(14分)设a n是公差不为零的等差数列,S n为其前n项和,满足a22+a32=a42+a52,S7=7(1)求数列a n的通项公式及前n项和S n;(2)试求所有的正整数m,使得为数列a n中的项.18.(16分)在平面直角坐标系xoy中,已知圆C1:(x+3)2+(y﹣1)2=4和圆C2:(x﹣4)2+(y﹣5)2=4(I)若直线l过点A(4,0),且被圆C1截得的弦长为,求直线l的方程;(II)设P(a,b)为平面上的点,满足:存在过点P的两条互相垂的直线l1与l2,l1的斜率为2,它们分别与圆C1和圆C2相交,且直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等,试求满足条件的a,b的关系式.19.(16分)照某学者的理论,假设一个人生产某产品单件成本为a元,如果他卖出该产品的单价为m元,则他的满意度为;如果他买进该产品的单价为n元,则他的满意度为.如果一个人对两种交易(卖出或买进)的满意度分别为h 1和h2,则他对这两种交易的综合满意度为.现假设甲生产A、B两种产品的单件成本分别为12元和5元,乙生产A、B两种产品的单件成本分别为3元和20元,设产品A、B的单价分别为m A元和m B 元,甲买进A与卖出B的综合满意度为h甲,乙卖出A与买进B的综合满意度为h乙.(1)求h甲和h乙关于m A、m B的表达式;当m A=m B时,求证:h甲=h乙;(2)设m A=m B,当m A、m B分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?(3)记(2)中最大的综合满意度为h0,试问能否适当选取m A、m B的值,使得h甲≥h0和h乙≥h0同时成立,但等号不同时成立?试说明理由.20.(16分)设a为实数,函数f(x)=2x2+(x﹣a)|x﹣a|.(1)若f(0)≥1,求a的取值范围;(2)求f(x)的最小值;(3)设函数h(x)=f(x),x∈(a,+∞),求不等式h(x)≥1的解集.2009年江苏省高考数学试卷参考答案与试题解析一、填空题(共14小题,每小题5分,满分70分)1.(5分)(2009•江苏)若复数z1=4+29i,z2=6+9i,其中i是虚数单位,则复数(z1﹣z2)i的实部为﹣20.【分析】把复数z1=4+29i,z2=6+9i,代入复数(z1﹣z2)i,化简,按多项式乘法法则,展开,化简为a+bi(a,b∈R)的形式,即可得到实部.【解答】解:∵z1=4+29i,z2=6+9i,∴(z1﹣z2)i=(﹣2+20i)i=﹣20﹣2i,∴复数(z1﹣z2)i的实部为﹣20.故答案为:﹣202.(5分)(2009•江苏)已知向量和向量的夹角为300,,则向量和向量的数量积=3.【分析】向量数量积公式的应用,条件中给出两个向量的模和向量的夹角,代入公式进行计算即可.【解答】解:由题意知:=2×=3,故答案为:3.3.(5分)(2009•江苏)函数f(x)=x3﹣15x2﹣33x+6的单调减区间为(﹣1,11).【分析】要求函数的单调减区间可先求出f′(x),并令其小于零得到关于x的不等式求出解集即可.【解答】解:f′(x)=3x2﹣30x﹣33=3(x2﹣10x﹣11)=3(x+1)(x﹣11)<0,解得﹣1<x<11,故减区间为(﹣1,11).故答案为:(﹣1,11)4.(5分)(2009•江苏)函数y=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0)在闭区间[﹣π,0]的图象如图所示,则ω=3.【分析】根据函数图象求出函数的周期T,然后求出ω.【解答】解:由图中可以看出:T=π,∴T=π=,∴ω=3.故答案为:35.(5分)(2009•江苏)现有5根竹竿,它们的长度(单位:m)分别为2.5,2.6,2.7,2.8,2.9,若从中一次随机抽取2根竹竿,则它们的长度恰好相差0.3m 的概率为0.2.【分析】由题目中共有5根竹竿,我们先计算从中一次随机抽取2根竹竿的基本事件总数,及满足条件的基本事件个数,然后代入古典概型计算公式,即可求出满足条件的概率.【解答】解:从5根竹竿中一次随机抽取2根的可能的事件总数为10,它们的长度恰好相差0.3m的事件数有2.5和2.8,2.6和2.9,共2个∴所求概率为0.2.故答案为:0.2.6.(5分)(2009•江苏)某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如表:学生1号2号3号4号5号甲班67787乙班67679则以上两组数据的方差中较小的一个为S2=0.4.【分析】根据表中所给的两组数据,先写出两组数据的平均数,再求出两组数据的方差,把方差进行比较,方差小的一个是甲班,得到结果.【解答】解:由题意知甲班的投中次数是6,7,7,8,7,这组数据的平均数是7,甲班投中次数的方差是,乙班的投中次数是6,7,6,7,9,这组数据的平均数是7,这组数据的方差是∴两组数据的方差中较小的一个为0.4,故答案为:0.47.(5分)(2009•江苏)如图是一个算法的流程图,最后输出的W=22.【分析】根据流程图可知,计算出S,判定是否满足S≥10,不满足则循环,直到满足就跳出循环,最后求出W值即可.【解答】解:由流程图知,第一次循环:T=1,S=1;不满足S≥10第二次循环:T=3,S=32﹣1=8;不满足S≥10第三次循环:T=5,S=52﹣8=17,满足S≥10此时跳出循环,∴W=5+17=22.故答案为228.(5分)(2009•江苏)在平面上,若两个正三角形的边长的比为1:2,则它们的面积比为1:4,类似地,在空间内,若两个正四面体的棱长的比为1:2,则它们的体积比为1:8.【分析】根据平面与空间之间的类比推理,由点类比点或直线,由直线类比直线或平面,由平面图形面积类比立体图形的体积,结合三角形的面积比的方法类比求四面体的体积比即可.【解答】解:平面上,若两个正三角形的边长的比为1:2,则它们的面积比为1:4,类似地,由平面图形面积类比立体图形的体积,得出:在空间内,若两个正四面体的棱长的比为1:2,则它们的体积比为1:8故答案为:1:8.9.(5分)(2009•江苏)在平面直角坐标系xOy中,点P在曲线C:y=x3﹣10x+3上,且在第二象限内,已知曲线C在点P处的切线斜率为2,则点P的坐标为(﹣2,15).【分析】先设切点P(x0,y0)(x0<0),根据导数的几何意义求出函数f(x)在x=x0处的导数,从而求出切线的斜率,建立方程,解之即可.【解答】解:设P(x0,y0)(x0<0),由题意知:y′|x=x0=3x02﹣10=2,∴x02=4.∴x0=﹣2,∴y0=15.∴P点的坐标为(﹣2,15).故答案为:(﹣2,15)10.(5分)(2009•江苏)已知,函数f(x)=log a x,若正实数m,n满足f(m)>f(n),则m,n的大小关系为m<n.【分析】因为已知条件中对数函数的底数,即0<a<1,故函数f(x)=log a x在(0,+∞)上为减函数,根据函数的单调性,结合足f(m)>f(n),不难判断出m,n的大小关系.【解答】解:∵∴0<a<1∴f(x)=log a x在(0,+∞)上为减函数若f(m)>f(n)则m<n故答案为:m<n11.(5分)(2009•江苏)已知集合A={x|log2x≤2},B=(﹣∞,a),若A⊆B则实数a的取值范围是(c,+∞),其中c=4.【分析】先化简集合A,然后根据子集的定义求出集合B的取值范围,总而求出所求.【解答】解:A={x|log2x≤2}={x|0<x≤4}而B=(﹣∞,a),∵A⊆B∴a>4即实数a的取值范围是(4,+∞),故答案为:412.(5分)(2009•江苏)设α和β为不重合的两个平面,给出下列命题:(1)若α内的两条相交直线分别平行于β内的两条直线,则α平行于β;(2)若α外一条直线l与α内的一条直线平行,则l和α平行;(3)设α和β相交于直线l,若α内有一条直线垂直于l,则α和β垂直;(4)直线l与α垂直的充分必要条件是l与α内的两条直线垂直.上面命题,真命题的序号是(1)(2)(写出所有真命题的序号)【分析】从线面平行、垂直的判定定理,判断选项即可.【解答】解:由面面平行的判定定理可知,(1)正确.由线面平行的判定定理可知,(2)正确.对于(3)来说,α内直线只垂直于α和β的交线l,得不到其是β的垂线,故也得不出α⊥β.对于(4)来说,l只有和α内的两条相交直线垂直,才能得到l⊥α.也就是说当l垂直于α内的两条平行直线的话,l不一定垂直于α.13.(5分)(2009•江苏)如图,在平面直角坐标系xoy中,A1,A2,B1,B2为椭圆=1(a>b>0)的四个顶点,F为其右焦点,直线A1B2与直线B1F相交于点T,线段OT与椭圆的交点M恰为线段OT的中点,则该椭圆的离心率为e=2﹣5.【分析】解法一:可先直线A1B2的方程为,直线B1F的方程为,联立两直线的方程,解出点T的坐标,进而表示出中点M的坐标,代入椭圆的方程即可解出离心率的值;解法二:对椭圆进行压缩变换,,,椭圆变为单位圆:x'2+y'2=1,F'(,0).根据题设条件求出直线B1T方程,直线直线B1T与x轴交点的横坐标就是该椭圆的离心率.【解答】解法一:由题意,可得直线A1B2的方程为,直线B1F的方程为两直线联立则点T(),则M(),由于此点在椭圆上,故有,整理得3a2﹣10ac﹣c2=0即e2+10e﹣3=0,解得故答案为解法二:对椭圆进行压缩变换,,,椭圆变为单位圆:x'2+y'2=1,F'(,0).延长TO交圆O于N,易知直线A 1B1斜率为1,TM=MO=ON=1,,设T(x′,y′),则,y′=x′+1,由割线定理:TB2×TA1=TM×TN,,(负值舍去),易知:B1(0,﹣1),直线B1T方程:令y′=0,即F横坐标即原椭圆的离心率e=.故答案:.14.(5分)(2009•江苏)设{a n}是公比为q的等比数列,|q|>1,令b n=a n+1(n=1,2,…),若数列{b n}有连续四项在集合{﹣53,﹣23,19,37,82}中,则6q=﹣9.【分析】根据B n=A n+1可知A n=B n﹣1,依据{Bn}有连续四项在{﹣53,﹣23,19,37,82}中,则可推知则{A n}有连续四项在{﹣54,﹣24,18,36,81}中,按绝对值的顺序排列上述数值,相邻相邻两项相除发现﹣24,36,﹣54,81是{A n}中连续的四项,求得q,进而求得6q.【解答】解:{Bn}有连续四项在{﹣53,﹣23,19,37,82}中B n=A n+1 A n=B n﹣1则{A n}有连续四项在{﹣54,﹣24,18,36,81}中{A n}是等比数列,等比数列中有负数项则q<0,且负数项为相隔两项等比数列各项的绝对值递增或递减,按绝对值的顺序排列上述数值18,﹣24,36,﹣54,81相邻两项相除=﹣=﹣=﹣=﹣很明显,﹣24,36,﹣54,81是{A n}中连续的四项q=﹣或q=﹣(|q|>1,∴此种情况应舍)∴q=﹣∴6q=﹣9故答案为:﹣9二、解答题(共6小题,满分90分)15.(14分)(2009•江苏)设向量(1)若与垂直,求tan(α+β)的值;(2)求的最大值;(3)若tanαtanβ=16,求证:∥.【分析】(1)先根据向量的线性运算求出,再由与垂直等价于与的数量积等于0可求出α+β的正余弦之间的关系,最后可求正切值.(2)先根据线性运算求出,然后根据向量的求模运算得到||的关系,最后根据正弦函数的性质可确定答案.(3)将tanαtanβ=16化成弦的关系整理即可得到(4cosα)•(4cosβ)=sinαsinβ,正是∥的充要条件,从而得证.【解答】解:(1)∵=(sinβ﹣2cosβ,4cosβ+8sinβ),与垂直,∴4cosα(sinβ﹣2cosβ)+sinα(4cosβ+8sinβ)=0,即sinαcosβ+cosαsinβ=2(cosαcosβ﹣sinαsinβ),∴sin(α+β)=2cos(α+β),cos(α+β)=0,显然等式不成立∴tan(α+β)=2.(2)∵=(sinβ+cosβ,4cosβ﹣4sinβ),∴||==,∴当sin2β=﹣1时,||取最大值,且最大值为.(3)∵tanαtanβ=16,∴,即sinαsinβ=16cosαcosβ,∴(4cosα)•(4cosβ)=sinαsinβ,即=(4cosα,sinα)与=(sinβ,4cosβ)共线,∴∥.16.(14分)(2009•江苏)如图,在直三棱柱ABC﹣A1B1C1中,E,F分别是A1B,A1C的中点,点D在B1C1上,A1D⊥B1C.求证:(1)EF∥平面ABC;(2)平面A1FD⊥平面BB1C1C.【分析】(1)要证明EF∥平面ABC,证明EF∥BC即可;(2)要证明平面A1FD⊥平面BB1C1C,通过证明A1D⊥面BB1C1C即可,利用平面与平面垂直的判定定理证明即可.【解答】证明:(1)因为E,F分别是A1B,A1C的中点,所以EF∥BC,又EF⊄面ABC,BC⊂面ABC,所以EF∥平面ABC;(2)因为直三棱柱ABC﹣A1B1C1,所以BB1⊥面A1B1C1,BB1⊥A1D,又A1D⊥B1C,BB1∩B1C=B1,所以A1D⊥面BB1C1C,又A1D⊂面A1FD,所以平面A1FD⊥平面BB1C1C.17.(14分)(2009•江苏)设a n是公差不为零的等差数列,S n为其前n项和,满足a22+a32=a42+a52,S7=7(1)求数列a n的通项公式及前n项和S n;(2)试求所有的正整数m,使得为数列a n中的项.【分析】(1)先把已知条件用a1及d表示,然后联立方程求出a1,d代入等差数列的通项公式及前n项和公式可求.(2)先把已知化简可得,然后结合数列a n的通项公式可寻求m满足的条件.【解答】解:(1)由题意可得联立可得a1=﹣5,d=2∴a n=﹣5+(n﹣1)×2=2n﹣7,(2)由(1)知=若使其为数列a n中的项则必需为整数,且m为正整数m=2,m=1;m=1时不满足题意,(a1=﹣5是最小值)故舍去.所以m=2.18.(16分)(2009•江苏)在平面直角坐标系xoy中,已知圆C1:(x+3)2+(y ﹣1)2=4和圆C2:(x﹣4)2+(y﹣5)2=4(I)若直线l过点A(4,0),且被圆C1截得的弦长为,求直线l的方程;(II)设P(a,b)为平面上的点,满足:存在过点P的两条互相垂的直线l1与l2,l1的斜率为2,它们分别与圆C1和圆C2相交,且直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等,试求满足条件的a,b的关系式.【分析】(I )因为直线l过点A(4,0),故可以设出直线l的点斜式方程,又由直线被圆C1截得的弦长为,根据半弦长、半径、弦心距满足勾股定理,我们可以求出弦心距,即圆心到直线的距离,得到一个关于直线斜率k的方程,解方程求出k值,代入即得直线l的方程.(II)根据题意,可以设出过P点的直线l1与l2的点斜式方程,分析可得圆C1的圆心到直线l1的距离和圆C2的圆心到直线l2的距离相等,即可以得到一个关于a、b的方程,整理变形可得答案.【解答】解:(Ⅰ)若直线l的斜率不存在,则直线x=4与圆C1不相交,故直线l的斜率存在,不妨设为k,则直线l的方程为y=k(x﹣4),即kx﹣y﹣4k=0圆C1圆心(﹣3,1)到直线的距离,直线l被圆C1截得的弦长为,则=1,联立以上两式可得k=0或,故所求直线l方程为y=0或.(Ⅱ)依题意直线的方程可设为l1:y﹣b=2(x﹣a),l2:,因为两圆半径相等,且分别被两直线截得的弦长相等,故圆C1的圆心到直线l1的距离和圆C2的圆心到直线l2的距离相等,即,解得:a﹣3b+21=0或3a+b﹣7=0.19.(16分)(2009•江苏)照某学者的理论,假设一个人生产某产品单件成本为a元,如果他卖出该产品的单价为m元,则他的满意度为;如果他买进该产品的单价为n元,则他的满意度为.如果一个人对两种交易(卖出或买进)的满意度分别为h 1和h2,则他对这两种交易的综合满意度为.现假设甲生产A、B两种产品的单件成本分别为12元和5元,乙生产A、B两种产品的单件成本分别为3元和20元,设产品A、B的单价分别为m A元和m B 元,甲买进A与卖出B的综合满意度为h甲,乙卖出A与买进B的综合满意度为h乙.(1)求h甲和h乙关于m A、m B的表达式;当m A=m B时,求证:h甲=h乙;(2)设m A=m B,当m A、m B分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?(3)记(2)中最大的综合满意度为h0,试问能否适当选取m A、m B的值,使得h甲≥h0和h乙≥h0同时成立,但等号不同时成立?试说明理由.【分析】(1)表示出甲和乙的满意度,整理出最简形式,在条件m A=m B时,表示出要证明的相等的两个式子,得到两个式子相等.(2)在上一问表示出的结果中,整理出关于变量的符合基本不等式的形式,利用基本不等式求出两个人满意度最大时的结果,并且写出等号成立的条件.(3)先写出结论:不能由(2)知h0=h0=.因为h甲h乙≤,不能取到m A,m B的值,使得h甲≥h0和h乙≥h0同时成立,但等号不同时成立.【解答】解:(1)甲:买进A的满意度为h A1=,卖出B的满意度为h B1=;所以,甲买进A与卖出B的综合满意度为h==;甲乙:卖出A的满意度为:h A2=,买进B的满意度为:h B2=;==;所以,乙卖出A与买进B的综合满意度h乙当m A=m B时,h甲=,h乙=,所以h甲=h乙(2)设m B=x(其中x>0),当m A=m B时,h甲=h乙==≤;当且仅当x=,即x=10时,上式“=”成立,即m B=10,m A=×10=6时,甲、乙两人的综合满意度均最大,最大综合满意度为;(3)不能由(2)知h0=.因为h甲h乙≤因此,不能取到m A,m B的值,使得h甲≥h0和h乙≥h0同时成立,但等号不同时成立.20.(16分)(2009•江苏)设a为实数,函数f(x)=2x2+(x﹣a)|x﹣a|.(1)若f(0)≥1,求a的取值范围;(2)求f(x)的最小值;(3)设函数h(x)=f(x),x∈(a,+∞),求不等式h(x)≥1的解集.【分析】(1)f(0)≥1⇒﹣a|a|≥1再去绝对值求a的取值范围,(2)分x≥a和x<a两种情况来讨论去绝对值,再对每一段分别求最小值,借助二次函数的对称轴及单调性.最后综合即可.(3)h(x)≥1转化为3x2﹣2ax+a2﹣1≥0,因为不等式的解集由对应方程的根决定,所以再对其对应的判别式分三种情况讨论求得对应解集即可.【解答】解:(1)若f(0)≥1,则﹣a|a|≥1⇒⇒a≤﹣1(2)当x≥a时,f(x)=3x2﹣2ax+a2,∴,如图所示:当x≤a时,f(x)=x2+2ax﹣a2,∴.综上所述:.(3)x∈(a,+∞)时,h(x)≥1,得3x2﹣2ax+a2﹣1≥0,△=4a2﹣12(a2﹣1)=12﹣8a2当a≤﹣或a≥时,△≤0,x∈(a,+∞);当﹣<a<时,△>0,得:即进而分2类讨论:当﹣<a<﹣时,a<,此时不等式组的解集为(a,]∪[,+∞);当﹣≤x≤时,<a<;此时不等式组的解集为[,+∞).综上可得,当a∈(﹣∞,﹣)∪(,+∞)时,不等式组的解集为(a,+∞);当a∈(﹣,﹣)时,不等式组的解集为(a,]∪[,+∞);当a∈[﹣,]时,不等式组的解集为[,+∞).。

高等代数(北大版)第一学期考试卷答案一、选择题(每小题3分,共24分)1.D2.C3.B4.D5.A6.B7.C8.A二、填空题(每小题3分,共18分)1.322(1)5(1)7(1)1x x x -+-+-- 2.2x + 3.1()2n n +- 4.)1,,1,1( c x = 5.d6.⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---=-3/13/1003/23/100005200211A三、计算题(本大题共3个小题,共22分.请写出必要的推演步骤和文字说明)1.(6分)设b ax x x x x f +++-=23463)(,1)(2-=x x g ,a 与b 是什么数时,)(x f 能被)(x g 整除?解:方法一、利用辗转相除法,得余式:7)3()(++-=b x a x r ,………………………………………..4分由已知, 7,3-==b a ……………………………………………..2分方法二、由于)(x f 能被)(x g 整除,而1)(2-=x x g 的零点为1和-1,所以1和-1也应是)(x f 的零点,即04)1(=++=b a f 和 010)1(=+-=-b a f …………5分 故7,3-==b a …………………………………………………...….1分2.(8分)已知B AX X +=,其中⎪⎪⎪⎭⎫ ⎝⎛---=101111010A ,⎪⎪⎪⎭⎫ ⎝⎛--=350211B ,求矩阵X 。
解:由 B AX X += 得 B X A E =-)(而 ⎪⎪⎪⎭⎫⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛----⎪⎪⎪⎭⎫ ⎝⎛=-201101011101111010100010001A E 可逆…………….2分可以求得 ⎪⎪⎪⎭⎫ ⎝⎛--=--11012312031)(1A E ……………………………………….. .3分 所以 ⎪⎪⎪⎭⎫ ⎝⎛--=-=-11012312031)(1B A E X ⎪⎪⎪⎭⎫ ⎝⎛--350211=⎪⎪⎪⎭⎫ ⎝⎛--110213………………3分3.(8)b a ,取什么值时,线性方程组⎪⎪⎩⎪⎪⎨⎧=-+++=+++=-+++=++++bx x x x x x x x x a x x x x x x x x x x 5432154325432154321334536223231有解?在有解的情形求一般解。

2009年江苏省普通高校“专转本”统一考试高等数学一、单项选择题(本大题共6小题,每小题4分,满分24分。
在每小题给出的四个选项中,只有一项是符合题目要求的,请将其字母标号填在题后的括号内。
)1、已知32lim 22=-++→x bax x x ,则常数a ,b 的取值分别为A 、2,1-=-=b aB 、0,2=-=b aC 、0,1=-=b aD 、1,2-=-=b a 2、已知函数423)(22-+-=x x x x f ,则2=x 为)(x f 的A 、跳跃间断点B 、可去间断点C 、无穷间断点D 、震荡间断点3、设函数⎪⎩⎪⎨⎧>≤=0,1sin 0,0)(x x x x x f a 在0=x 处可导,则常数a的取值范围是A 、10<<aB 、10≤<aC 、1>aD 、1≥a 4、曲线2)1(12-+=x x y 的渐近线条数为A 、1B 、2C 、3D 、45、设)13ln()(+=x x F 是函数)(x f 的一个原函数,则=+⎰dx x f )12('A 、C x ++461B 、C x ++463C 、C x ++8121D 、Cx ++81236、设a 为非零常数,则数项级数∑∞=+12n nan A 、条件收敛B 、绝对收敛C 、发散D 、敛散性与a 有关二、填空题(本大题共6小题,每小题4分,满分24分)7、已知2)(lim =-∞→x x Cx x ,则常数=C 8、设函数⎰=x t te x 20)(ϕ,则=)('x ϕ9、已知向量)1,0,1(-=→a ,)1,2,1(-=→b ,则→→+b a 与→a 的夹角为10、设函数),(y x z z =由方程12=+yz xz 所确定,则=∂∂x z 11、若幂级数n n n x na ∑∞=12)0(>a 的收敛半径为21,则常数=a 12、微分方程0)2()1(2=--+xdy y ydx x 的通解为三、计算题(本大题共8小题,每小题8分,满分64分)13、求极限xx x x sin lim 30-→14、设函数)(x y y =由参数方程⎩⎨⎧-+=+=32)1ln(2t t y t x 所确定,求dt dy ,22dx y d 15、求不定积分dx x ⎰+12sin 16、求定积分dxx x ⎰-1022217、求通过直线12213-=-=z y x 且垂直于平面02=+++z y x 的平面方程.18、计算二重积分⎰⎰D ydxdy,其中{}2,2,20|),(22≥+≤≤≤≤=y x y x x y x D .19、设),(sin xy x f z =,其中f 具有二阶连续偏导数,求yx z ∂∂∂2.20、求微分方程x y y =-'''的通解.四、综合题(本大题共2小题,每小题10分,满分20分)21、已知13)(3+-=x x x f ,试求:(1)函数)(x f 的单调区间与极值;(2)曲线)(x f y =的凹凸区间与拐点;(3)函数)(x f 在闭区间[]3,2-上的最大值和最小值.22、设1D 是由抛物线22x y =和直线0,==y a x 所围成的平面区域,2D 是由抛物线22x y =和直线a x =,2=x 及0=y 所围成的平面区域,其中20<<a .试求:(1)1D 绕y 轴旋转而成的旋转体的体积1V ,以及2D 绕x 轴旋转而成的旋转体的体积2V ;(2)常数a 的值,使得1D 的面积与2D 的面积相等.五、证明题(本大题共2小题,每小题9分,满分18分)23、已知⎩⎨⎧≥+<=-010)(x x x e x f x ,证明)(x f 在0=x 处连续但不可导.24、证明:当21<<x 时,32ln 42-+>x x x x .。
09年高考试题精选苏大2009年江苏省高考试题 测试题2019.91,将圆()3122=++y x 绕直线01=--y kx 旋转一周,所得几何体的体积为 .2,1. 某单位为了了解用电量y (度)与气温x (°C )之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:由表中数据得线性回归方程中 ,预测当气温为 时,用电量的度数约为 .3,如图,在Rt △ABC 中,AC ⊥BC ,D 在边AC 上,已知BC =2,CD =1,∠ABD =45°,则AD = .4,经过抛物线上一点A (-2,2)的直线与抛物线的另一交点为B ,若抛物线在A ,B 两处的切线互相垂直,则直线AB 的斜率为 .5, 抛掷一颗骰子的点数为a ,得到函数,则“)(x f y = 在[0,4]上至少有5个零点”的概率是 .6,按右图所示的流程图运算,则输出的z = . ˆybx a =+2b =-4C -︒DC B A212y x =π()sin()3a f x x =7, 等边△ABC 中,P 在线段AB 上,且 ,若 ,则实数 的值是 .8,在平面直角坐标系中,不等式组 (a 为常数)表示的平面区域的面积是4,则y x +2 的最小值为 .9,从一个半径为1的圆形铁片中剪去圆心角为x 弧度的一个扇形,将余下的部分卷成一个圆锥(不考虑连接用料),当圆锥的容积达到最大时,x 的值是 .10,若 ≥ 对一切x >0恒成立,则a 的取值范围是 .(第8题)AP PB λ=CP AB PB AC ⋅=⋅λ0,0,,x y x y x a +⎧⎪-⎨⎪⎩≥≥≤1||x a x -+12测试题答案1, 2, 68 3, 54, - 5, 6, 305 7, 2 8,10, a ≤2342314-。
2009年普通高等学校招生全国统一考试(江苏卷)数学Ⅰ参考公式:样本数据12,,,n x x x 的方差221111(),n n i ii i s x x x x n n ===-=∑∑其中一、填空题:本大题共14小题,每小题5分,共70分。
1.若复数12429,69z i z i =+=+,其中i 是虚数单位,则复数12()z z i -的实部为______2.已知向量a和向量b的夹角为30,||2,||3==a b ,则向量a和向量b的数量积=a b __________ .3.函数32()15336f x x x x =--+的单调减区间为_____4.函数s i n ()(y A x A ωϕωϕ=+为常数,0,0)A ω>>在闭区间[,0]π-上的图象如图所示,则ω=_______ .5.现有5根竹竿,它们的长度(单位:m )分别为2.5,2.6,2.7,2.8,2.9,若从中一次随机抽取2根竹竿,则它们的长度恰好相差0.3m 的概率为________ .6.某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如下表:学生 1号 2号 3号 4号 5号 甲班 6 7 7 8 7 乙班6767911 π-23π-3π-O xy则以上两组数据的方差中较小的一个为2s=________ .7.右图是一个算法的流程图,最后输出的W =________ .8.在平面上,若两个正三角形的边长的比为1:2,则它们的面积比为1:4,类似地,在空间,若两个正四面体的棱长的比为1:2,则它们的体积比为________ .9.在平面直角坐标系xoy 中,点P 在曲线3:103C y x x =-+上,且在第二象限内,已知曲线C 在点P 处的切线的斜率为2,则点P 的坐标为________.10.已知512a -=,函数()xf x a =,若实数,m n满足()()f m f n >,则,m n 的大小关系为 _______. 11.已知集合{}2|log 2A x x =≤,(,)B a =-∞,若A B ⊆则实数a 的取值范围是(,)c +∞,其中c =________ .12.设α和β为不重合的两个平面,给出下列命题:(1)若α内的两条相交直线分别平行于β内的两条直线,则α平行于β;(2)若α外一条直线l 与α内的一条直线平行,则l 和α平行;(3)设α和β相交于直线l ,若α内有一条直线垂直于l ,则α和β垂直;(4)直线l 与α垂直的充分必要条件是l 与α内的两条直线垂直.上面命题中,真命题的序号________(写出所有真命题的序号). 13.如图,在平面直角坐标系xoy 中,1212,,,A A B B 为椭圆22221(0)x ya b a b +=>>的四个顶点,F 为其右焦点,直线12A B 与直线1B F 相交于点T ,线段OT 与椭圆的交点M 恰为线段OT的中点,则该椭圆的离心率为________. 14.设{}n a 是公比为q的等比数列,||1q >,令1(1,2,n n b a n =+=若数列{}n b 有连续四项在集合xyA1 B2A2 OTM开始0S ← 1T ←2S T S ←-10S ≥2T T ←+W S T ←+输出W 结束YN{}53,23,19,37,82--中,则6q = ________二、解答题:本大题共6小题,共计90分。
绝密★启用前2009年普通高等学校招生全国统一考试(江苏卷)数学参考公式:样本数据1x,2x,,nx的标准差(ns x x=++-其中x为样本平均数柱体体积公式V Sh=其中S为底面积,h为高一、填空题:本大题共1小题,每小题5分,共70分.1.若复数z1=4+29i,z2=6+9i,其中i是虚数单位,则复数(z1−z2)i的实部为▲.【答案】−20.【解析】z1−z2=−2+20i,故(z1−z2)i=−20−2i.【说明】考查复数的四则运算.2.已知向量a和向量b的夹角为30︒,|a|=2,|b|=3,则向量a和向量b的数量积a·b= ▲.【答案】3.【解析】cos23θ===a b a b.【说明】考查向量的数量积(代数)运算.锥体体积公式13V Sh=其中S S为底面积,h为高球的表面积、体积公式24S Rπ=,343V Rπ=3. 函数f (x )=x 3−15x 2−33x +6的单调减区间为 ▲ . 【答案】(1,11)-.【解析】2()330333(11)(1)f x x x x x =--=-+',由(11)(1)0x x -+<得单调减区间为(1,11)-.【说明】考查函数的单调性,考查导数在研究函数性质中的应用.4. 函数y =A sin(ωx +φ)(A ,ω,φ为常数,A >0,ω>0)2π3-在闭区间[−π,0]上的图象如图所示,则ω= ▲ . 【答案】3.【解析】如图,2π3T =,所以3ω=.【说明】考查三角函数的图象和性质,考查周期性的概念.5. 现有5根竹竿,它们的长度(单位:m )分别为2.5,2.6,2.7,2.8,2.9,若从中一次随机抽取2根竹竿,则它们的长度恰好相差0.3m 的概率为 ▲ . 【答案】0.2 【解析】随机抽取2根竹竿的取法有10种,而长度恰好相差0.3m 的取法有2种,所以概率为0.2. 【说明】考查古典概型.6. 某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如下表:则以上两组数据的方差中较小的一个2s 为 ▲ .【答案】25.【解析】第一组数据7x =甲,212(10010)55S =++++=甲;第二组数据7x =乙,245S =乙.【说明】考查总体特征数的估计.实际上,根据数据的分布,知甲班的数据较为集中(甲班极差为2,众数为7,乙班极差为3,众数为6,7). 7. 右图是一个算法的流程图,最后输出的W = ▲ . 【答案】22. 【解析】追踪表:故出循环时,S =17,T =5,故W=22.【说明】本题考查算法初步,考查流程图(循环结构).值得注意的是,本题的循环结构并非是教材中所熟悉的当型或直到型,因此该流程图是一个非结构化的流程图,对学生的识图能力要求较高.8. 在平面上,若两个正三角形的边长的比为1:2,则它们的面积比为1:4.类似地,在空间中,若两个正四面体的棱长的比为1:2,则它们的体积比为 ▲ . 【答案】1:8【解析】由题意知,面积比是边长比的平方,由类比推理知:体积比是棱长比的立方. 【说明】本题考查合情推理之类比推理.9. 在平面直角坐标系xOy 中,点P 在曲线C :y =x 3−10x +3上,且在第二象限内,已知曲线C在点P 处的切线的斜率为2,则点P 的坐标为 ▲ . 【答案】(2,15)-.【解析】设点P 的横坐标为x 0,由2310y x '=-知203102x -=,又点P 在第二象限,02x =-,所以(2,15)P -.【说明】本题考查导数的几何意义——曲线切线的斜率.10. 已知a =f (x )=a x ,若实数m ,n 满足f (m )>f (n ),则m ,n 的大小关系为 ▲.【答案】m n <【解析】由01<<知01a <<,函数()x f x a =是减函数,由()()f m f n >知m n <.【说明】本题考查函数的单调性,指数函数的性质等概念.11. 已知集合A ={x |log 2x ≤2},B =(−∞,a ),若A ⊆B ,则实数a 的取值范围是(c ,+∞),其中c =▲ . 【答案】4【解析】由log 2x ≤2得0<x ≤4,(0,4]A =;由A B ⊆知4a >,所以c =4.【说明】本题考查对数函数的性质,集合间的基本关系(子集)等概念. 12. 设α 和β为不重合的两个平面,给出下列命题:(1)若α 内的两条相交直线分别平行于β内的两条直线,则α 平行于β; (2)若α 外一条直线l 与α 内的一条直线平行,则l 和α 平行;(3)设α 和β相交于直线l ,若α 内有一条直线垂直于l ,则α 和β垂直; (4)直线l 与α 垂直的充分必要条件是l 与α 内的两条直线垂直. 上面命题中,真命题的序号 ▲ .(写出所有真命题的序号). 【答案】(1)(2)【解析】由线面平行的判定定理知,(2)正确;相应地(1)可转化为一个平面内有两相交直线分别平行于另一个平面,所以这两个平面平行.【说明】本题考查空间点、线、面的位置关系.具体考查线面、面面平行、垂直间的关系与转化. 13. 如图,在平面直角坐标系xOy 中,A 1,A 2,B 1,B 2为椭圆22221(0)y x a b a b +=>>的四个顶点,F 为其右焦点,直线A 1B 2与直线B 1F 相交于点T ,线段OT 与椭圆的交点M 恰为线段O T 的中点,则该椭圆的离心率为 ▲ .【答案】5【解析】直线12A B 的方程为1y x a b +=-,直线1B F 的方程为1yx c b+=-,两方程联立方程组得T 2(,)ac ab bc a c a c+--,则点M (,)2()ac ab bc a c a c +--,由点M 在椭圆上,代入整理得:223100a ac c --=,23100e e --=,又 0e >,所以离心率为5.【说明】本题考查椭圆的概念、标准方程与几何性质.14. 设{a n }是公比为q 的等比数列,|q |>1,令b n =a n +1(n =1,2,…)若数列{b n }有连续四项在集合{−53,−23,19,37,82}中,则6q = ▲ . 【答案】9-【解析】由条件知数列{a n }中连续四项在集合{}54,24,18,36,81--中,由||1q >,所以{a n }中连续四项可能为(1)24-,36,54-,81,32q =-,69q =-;(2)18,24-,36,54-,不合;其它情形都不符合.【说明】本题考查等比数列的概念与通项公式.在本题中,如果将集合中的各数均除以3,得到集合{}232323,2,23,32,3-⨯-⨯⨯,再从其中选出四个数进行适当地排列,这样的解法更利于看清问题本质.二、解答题:本大题共6小题,共计90分,请在答题卡指定区域内作答,解答时应写出文字说明、证明或演算步骤.15. (本小题满分14分)设向量a =(4cos α ,sin α ),b =(sin β,4cos β),c =(cos β,−sin β), (1)若a 与b −2c 垂直,求tan(α +β)的值; (2)求+b c 的最大值;(3)若tan α tan β=16,求证:a ∥b . 【解析】(1)∵a ⊥b −2c ,∴(2)20⋅-=⋅-⋅=a b c a b a c .即4sin()8cos()0αβαβ+-+=,∴tan()2αβ+=. (2)(sin cos ,4cos 4sin )ββββ+=+-b c ,()()222sin cos 16cos sin ββββ+=++-b c 1730sin cos ββ=-1715sin 2β=-,∴当sin2β=−1时,2+b c 最大值为32,所以+b c的最大值为(3)∵tan tan 16αβ=,∴sin sin 16cos cos αβαβ=,即4cos 4cos sin sin 0αβαβ⋅-=, 所以a ∥b .16. (本小题满分14分)如图,在直三棱柱ABC −A 1B 1C 1中,E ,F 分别是A 1B ,A 1C 的中点,点D 在B 1C 1上,A 1D ⊥B 1C . 求证:(1)EF ∥平面ABC ; (2)平面A 1FD ⊥平面BB 1C 1C .【解析】(1)因为E ,F 分别是A 1B ,A 1C 的中点,所以EF ∥BC ,又EF ⊄平面ABC ,BC ⊂平面ABC ,∴EF ∥平面ABC ; (2)在直三棱柱ABC −A 1B 1C 1中,1111BB A BC ⊥面,AB CA 1B 1C 1 EF D第16题图∵A 1D ⊂平面A 1B 1C 1,∴11BB AD ⊥. 又11AD BC ⊥,BB 1 B 1C =B 1,∴111AD BC C ⊥面B . 又11AD AFD ⊂面,所以平面A 1FD ⊥平面BB 1C 1C .17. (本小题满分14分)设{a n }是公差不为零的等差数列,S n 为其前n 项和,满足22225234a a a a +=+,S 7=7. (1)求数列{a n }的通项公式及前n 项和S n ; (2)试求所有的正整数m ,使得12m m m a a a ++为数列{S n }中的项. 【解析】(1)设公差为d ,则22225243a a a a -=-,由性质得43433()()d a a d a a -+=+,因为0d ≠,所以430a a +=,即1250a d +=,又由77S =得176772a d ⨯+=,解得15a =-,2d =所以{}n a 的通项公式为27n a n =-,前n 项和26n S n n =-. (2)12(27)(25)(23)m m m m m a a a m ++--=-,令23m t -=,12(4)(2)m m m t t a a a t++--=86t t =+-,因为t 是奇数,所以t 可取的值为1±,当1t =,2m =时,863t t +-=,2573⨯-=,是数列{}n a 中的项;1t =-,1m =时,8615t t +-=-,数列{}n a 中的最小项是5-,不符合.所以满足条件的正整数2m =. 18. (本小题满分16分)在平面直角坐标系xOy 中,已知圆C 1∶(x +3)2+(y −1)2=4和圆C 2∶(x −4)2+(y −5)2=4.(1)若直线l 过点A (4,0),且被圆C 1截得的弦长为l 的方程;(2)设P 为平面上的点,满足:存在过点P 的无穷多对互相垂的直线l 1和l 2,它们分别与圆C 1和圆C 2相交,且直线l 1被圆C 1截得的弦长与直线l 2被圆C 2截得的弦长相等,试求所有满足条件的点P 的坐标.【解析】(1) 0y =或7(4)24y x =--,(2)法一)设点P (,)a b ,1l :()y b k x a -=-,则2l :1()y b x a k -=--由截得的弦长相等可得1C 到1l 与2C 到2l 的距离相等,即第18题图11|4()5()|a bk k----+=,即|31||45|k ka b k a kb---+=--++,整理得:222222(3)2(3)(1)(1)(5)2(4)(5)(4)a k ab k b b k a b k a+++-+-=-+--+-因为有无数组解,所以对应项系数相等,解得:32a=-,132b=;或52a=,12b=-.所以满足条件的点P坐标为313(,)22-或51(,)22-.法二)依题意点P在线段1C2C的中垂线上,且与1C、2C构成等腰直角三角形,设点P(,)a b,则713()42b a-=--,又120PC PC⋅=,即22670a b a b+---=,解得:32a=-,132b=;或52a=,12b=-.满足条件的点P坐标为313(,)22-或51(,)22-.19.(本小题满分16分)按照某学者的理论,假设一个人生产某产品单件成本为a元,如果他卖出该产品的单价为m元,则他的满意度为mm a+;如果他买进该产品的单价为n元,则他的满意度为nn a+.如果一个人对两种交易(卖出或买进)的满意度分别为h1和h2,现假设甲生产A,B两种产品的单件成本分别为12元和5元,乙生产A,B两种产品的单件成本分别为3元和20元,设产品A,B的单价分别为m A元和m B元,甲买进A与卖出B的综合满意度为h甲,乙卖出A与买进B的综合满意度为h乙.(1)求h甲和h乙关于m A,m B的表达式;当35A Bm m=时,求证:h甲=h乙;(2)设35A Bm m=,当m A,m B分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?(3)记(2)中最大的综合满意度为h0,试问能否适当选取m A,m B的值,使得0h h甲≥和h h乙≥同时成立,但等号不同时成立?试说明理由.【解析】h=甲h=乙当35A Bm m=时,h=甲h=乙h甲=h乙.当35A Bm m=时,h==甲,而520Bm≤≤,所以当20Bm=时,甲、乙两人的综合满意度均最大,此时12Am=.(3≥即31024120A B A B m m m m ≥++ ①且3406120A B A B m m m m ≥++ ②, 由①及520B m ≤≤得:24120310B A B m m m +≥-,又241202008[12,48]310310B B B m m m +=+∈--, 只有当12A m =,20B m =时,不等式①成立. 由②及312A m ≤≤得:4012036A B A m m m +≥-,又4012040200[20,80]36336A A A m m m +=+∈--, 只有当20B m =,12A m =时,不等式②成立.综上,不存在满足条件的A m 、B m 的值.20. (本小题满分16分)设a 为实数,函数f (x )=2x 2+(x −a )|x −a |. (1)若f (0)≥1,求a 的取值范围; (2)求f (x )的最小值;(3)设函数h (x )=f (x ),x ∈(a ,+∞),直接写出(不需给出演算步骤)不等式h (x )≥1的解集. 【解析】(1)若(0)1f ≥,即||1a a -≥,则{21a a <≥,所以1a ≤-. (2)当x a ≥时,22()32,f x x ax a =-+22min(),02,0()2(),0,033f a a a a f x a a f a a ≥≥⎧⎧⎪⎪==⎨⎨<<⎪⎪⎩⎩当x a ≤时,22()2,f x x ax a =+-{{2min2(),02,0()(),02,0f a a a a f x f a a a a -≥-≥==<<综上22min2,0()2,03a a f x a a -≥⎧⎪=⎨<⎪⎩. (3)x a ≥时,()1h x ≥得223210x ax a -+-≥,222412(1)128a a a ∆=--=-,①当a a ≤≥时,0∆≤,不等式的解集为(,)a +∞;②当a <<0,∆>得(0x x x a⎧⎪≥⎨>⎪⎩, ia <<时,不等式的解集为(,)a +∞; ii)a ≤≤)+∞;iii)a <<时,不等式的解集为3([)3a a +-+∞.数学Ⅱ(附加题)参考公式:2222(1)(21)123.6n n n n ++++++=21. [选做题]在A 、B 、C 、D 四小题中只能选做两题........ A.选修4 - 1:几何证明选讲如图,在四边形ABCD 中,△ABC ≌△BAD .求证:AB ∥CD .证明:由△ABC ≌△BAD 得∠ACB =∠BDA ,故A 、B 、C 、D 四点共圆,从而∠CBA =∠CDB .再由△ABC ≌△B AD 得∠CAB =∠DBA .因此∠DBA =∠CDB ,所以AB ∥CD . B. 选修4 - 2:矩阵与变换,求矩阵3221A ⎡⎤=⎢⎥⎣⎦的逆矩阵. 解:设矩阵A 的逆矩阵为,x y z w ⎡⎤⎢⎥⎣⎦则3210,2101x y z w ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦即323210,2201x z y w x z y w ++⎡⎤⎡⎤=⎢⎥⎢⎥++⎣⎦⎣⎦故321,320,20,21,x z y w x z y w +=+=⎧⎧⎨⎨+=+=⎩⎩ 解得1,2,2,3x z y w =-===-, 从而A 的逆矩阵为11223A --⎡⎤=⎢⎥-⎣⎦.C. 选修4 - 4:坐标系与参数方程已知曲线C 的参数方程为1,13()x t ty t t ⎧=-⎪⎪⎨⎪=+⎪⎩(t 为参数,0t >).求曲线C 的普通方程.解:因为212,x t t=+-所以212,3y x t t +=+= 故曲线C 的普通方程为:2360x y -+=. D. 选修4 - 5:不等式选讲设a ≥b >0,求证:3332a b +≥2232a b ab +.证明:3322222232(32)3()2()(32)().a b a b ab a a b b b a a b a b +-+=-+-=--因为a ≥b >0,所以a b -≥0,2232a b ->0,从而22(32)()a b a b --≥0,即3332a b +≥2232a b ab +.22. 在平面直角坐标系xOy 中,抛物线C 的顶点在原点,经过点A (2,2),其焦点F 在x轴上(如图).(1)求抛物线C 的标准方程;(2)求过点F ,且与直线OA 垂直的直线的方程;(3)设过点(,0)(0)M m m >的直线交抛物线C 于D 、E 两点,ME =2DM ,记D 和E 两点间的距离为()f m ,求()f m 关于m 的表达式.23. 对于正整数n ≥2,用n T 表示关于x 的一元二次方程220x ax b ++=有实数根的有序数组(,)a b 的组数,其中{},1,2,,a b n ∈(a 和b 可以相等);对于随机选取的{},1,2,,a b n ∈(a 和b 可以相等),记n P 为关于x 的一元二次方程220x ax b ++=有实数根的概率。