2018年数学同步优化指导练习：第3章 2.2 最大值、最小值问题 活页14

活页作业(十四)　最大值、最小值问题1．已知函数y ＝－x 2－2x ＋3在[a,2]上的最大值为，则a 等于( )154A ．－　B ．　3212C ．－　D ．或－121232解析：对y 求导得y ′＝－2x －2.令y ′＝0，得x ＝－1.当a ≤－1时，最大值为f (－1)＝4，不合题意．当－1<a <2时，f (x )在[a,2]上是减少的，最大值为f (a )＝－a 2－2a ＋3＝，154解得a ＝－或a ＝－(舍去)．1232答案：C2．f (x )＝x 3－3x 2＋2在区间[－1,1]上的最大值是( )A ．－2B ．0C ．2D ．4解析：对y 求导得f ′(x )＝3x 2－6x ＝3x (x －2)．令f ′(x )＝0可得x ＝0或x ＝2(舍去)，当－1≤x <0时，f ′(x )>0；当0<x ≤1时，f ′(x )<0.所以当x ＝0时，f (x )取得最大值为2.答案：C3．要做一个圆锥形的漏斗，其母线长为20 cm ，要使其体积最大，则高为( )A ． cmB ． cm331033C ． cmD ． cm16332033解析：设圆锥的高为x cm ，则底面半径为cm ，202－x 2其体积为V ＝πx (202－x 2)(0<x <20)，13V ′＝π(400－3x 2)，令V ′＝0，13解得x 1＝，x 2＝－(舍去)．20332033当0<x <时，V ′>0；2033当<x <20时，V ′<0.2033∴当x ＝时，V 取最大值．2033答案：D4．已知某生产厂家的年利润y (单位：万元)与年产量x (单位：万件)的函数关系式为y ＝－x 3＋81x －234，则使该生产厂家获得最大年利润的年产量为( )13A ．13万件B ．11万件C ．9万件D ．7万件解析：x >0，y ′＝－x 2＋81＝(9－x )(9＋x )，令y ′＝0，解得x ＝9.∴x ∈(0,9)时，y ′>0；x ∈(9，＋∞)时，y ′<0.∴x ＝9时函数取得最大值．答案：C 5．用长为18m 的钢条围成一个长方体形状的框架，要求长方体的长与宽之比为2∶1，则该长方体的最大体积为( )A ．2 m 3B ．3 m 3C ．4 m 3D ．5 m 3解析：设长方体的宽为x m ，则长为2x m ，高为h ＝(4.5－3x )m .(0<x <32)∴长方体的体积为V (x )＝2x 2(4.5－3x )＝9x 2－6x 3.(0<x <32)∴V ′(x )＝18x －18x 2＝18x (1－x )．令V ′(x )＝0，解得x ＝1或x ＝0(舍去)．当0<x <1时，V ′(x )>0；当1<x <时，V ′(x )<0.32∴在x ＝1处V (x )取得极大值，并且这个极大值就是V (x )的最大值．∴最大体积V max ＝V (1)＝9×12－6×13＝3(m 3)．答案：B6．f (x )＝x 3－12x ＋8在[－3,3]上的最大值为M ，最小值为m ，则M －m ＝________.解析：f ′(x )＝3x 2－12.由f ′(x )>0，得x >2或x <－2；由f ′(x )<0，得－2<x <2.∴f (x )在[－3，－2]上是增加的，在[－2,2]上是减少的，在[2,3]上是增加的．又f (－3)＝17，f (－2)＝24，f (2)＝－8，f (3)＝－1，∴最大值M ＝24，最小值m ＝－8.∴M －m ＝24－(－8)＝32.答案：327．在半径为r 的圆内，作内接等腰三角形，当底边上的高为________时，它的面积最大．解析：如右图，设∠OBC ＝θ，则0<θ<，OD ＝r sin θ，BD ＝r cos θ.π2∴S △ABC ＝r cos θ(r ＋r sin θ)＝r 2cos θ＋r 2sin θcos θ.令S ′△ABC ＝－r 2sin θ＋r 2(cos 2θ－sin 2θ)＝0，得cos 2θ＝sin θ.又0<θ<，π2∴θ＝.即当θ＝时，△ABC 的面积最大．π6π6∴高为OA ＋OD ＝r ＋＝时面积最大．r23r2答案：3r 28．函数y ＝x ＋2cos x 在区间上的最大值是________．[0，π2]解析：对f (x )求导得f ′(x )＝1－2sin x .由f ′(x )＝0，得x ＝.π6∴在上，f ′(x )＞0，(0，π6)在上，f ′(x )＜0.(π6，π2)∴在x ＝处f (x )取到极大值也是最大值f ＝＋.π6(π6)π63答案：＋π639．已知函数f (x )＝x 2－ln x －ax ，a ∈R .(1)当a ＝1时，求f (x )的最小值；(2)若f (x )>x ，求a 的取值范围．解：(1)当a ＝1时，f (x )＝x 2－ln x －x ，f ′(x )＝.(2x ＋1)(x －1)x当x ∈(0,1)时，f ′(x )<0；当x ∈(1，＋∞)时，f ′(x )>0.∴f (x )的最小值为f (1)＝0.(2)由f (x )>x ，得f (x )－x ＝x 2－ln x －(a ＋1)x >0.∵x >0，∴f (x )>x 等价于x －>a ＋1.ln xx 令g (x )＝x －，则g ′(x )＝.ln xx x 2－1＋ln xx 2当x ∈(0,1)时，g ′(x )<0；当x ∈(1，＋∞)时，g ′(x )>0.∴g (x )有最小值g (1)＝1.∴a ＋1<1，即a 的取值范围是(－∞，0)．10．某网球中心欲建连成片的网球场数块，用128万元购买土地10 000 m 2，该中心每块球场的建设面积为1 000 m 2，球场每平方米的平均建设费用与球场数有关，当该中心建球场x 块时，每平方米的平均建设费用(单位：元)可近似地用f (x )＝800来刻(1＋15ln x )画．为了使该球场每平方米的综合费用最省(综合费用是建设费用与购地费用之和)，该网球中心应建几块球场？解：设建成x 个球场，则1≤x ≤10，每平方米的购地费用为＝元．128×1041 000x1 280x ∵每平方米的平均建设费用(单位：元)可近似地用f (x )＝800来表示，(1＋15ln x )∴每平方米的综合费用为g (x )＝f (x )＋＝800＋160ln x ＋(x >0)，1 280x 1 280x ∴g ′(x )＝(x >0)．160(x －8)x 2令g ′(x )＝0，则x ＝8.当0<x <8时，g ′(x )<0；当x >8时，g ′(x )>0.∴当x ＝8时，函数取得极小值，且为最小值．故当建成8块球场时，每平方米的综合费用最省．11．某工厂生产某种产品，已知该产品的月产量x (t)与每吨产品的价格P (元/t)之间的关系式为P ＝24 200－x 2，且生产x t 的成本为C ＝50 000＋200x (元)，则月产量为多少t 时，15利润达到最大值？( )A ．100B ．160C ．200D ．240解析：根据题意，列出函数关系式，求导求解．每月生产x t 时的利润为f (x )＝x －(50 000＋200x )＝(24 200－15x 2)－x 3＋24 000x －50 000(x ≥0)．15令f ′(x )＝－x 2＋24 000＝0，35解得x 1＝200，x 2＝－200(舍去)．∵f (x )在[0，＋∞)内只有一个点x ＝200使f ′(x )＝0，∴它就是最大值点，且最大值为f (200)＝－×2003＋24 000×200－50 000＝3 150 000(元)．15∴每月生产200 t 产品时利润达到最大，最大利润为315万元．答案：C12．容积为256的方底无盖水箱，它的高为________时用料最省．解析：设方底无盖水箱的底面边长为a ，高为h ，则V ＝a 2h ＝256，即h ＝.256a 2用料最省，即表面积最小，由题意列式如下：S 表＝S 底＋S 侧＝a 2＋4ah ＝a 2＋4a ＝a 2＋256a 2 1 024aS ′＝2a －.1 024a 2令S ′＝0，即2a －＝0，解得a ＝8.1 024a 2当0<a <8时，S ′<0；当a >8时，S ′>0.∴当a ＝8时，S 表取得极小值，也是最小值．∴h ＝＝4.25664答案：413．函数f (x )＝5－36x ＋3x 2＋4x 3在区间[－2，＋∞)上的最大值为________，最小值为________．解析：∵f ′(x )＝－36＋6x ＋12x 2，令f ′(x )＝0，解得x 1＝－2，x 2＝.32当x >时，f (x )是增加的；32当－2≤x ≤时，f (x )是减少的．32∴在[－2，＋∞)上无最大值．又f ＝－28，(32)34∴最小值为－28.34答案：不存在　－283414．函数f (x )＝，当－6≤x ≤8时的最大值为________，最小值为________．100－x 2解析：f ′(x )＝－，令f ′(x )＝0，得x ＝0.x100－x 2又f (－6)＝8，f (0)＝10，f (8)＝6.∴f (x )min ＝6，f (x )max ＝10.答案：10　615．已知某公司生产某品牌服装的年固定成本为10万元，每生产1千件需另投入2.7万元，设该公司一年内共生产该品牌服装x 千件并全部销售完，每销售1千件的收入为R (x )万元，且R (x )＝Error!(1)写出年利润W (万元)关于年产量x (千件)的函数关系式；(2)年产量为多少千件时，该公司在这一品牌服装的生产中所获年利润最大？解：(1)当0<x ≤10时，W ＝xR (x )－(10＋2.7x )＝8.1x －－10；x 330当x >10时，W ＝xR (x )－(10＋2.7x )＝98－－2.7x .1 0003x ∴W ＝Error!(2)当0<x ≤10时，令W ′＝8.1－＝0，得x ＝9.x 210且x ∈(0,9)时，W ′>0；x ∈(9,10)时，W ′<0.∴当x ＝9时，W 取极大值，也是最大值，且W max ＝8.1×9－×93－10＝38.6；130当x >10时，令W ′＝－2.7＝0，得x ＝.1 0003x 21009当x ∈时，W ′>0；(10，1009)当x ∈时，W ′<0.(1009，＋∞)∴当x ＝时，W 取极大值，也是最大值，1009且W max ＝98－－2.7×＝38.10003×10091003综上可知，x ＝9时，W 有最大值38.6，即年产量为9千件时，该公司所获年利润最大．16．已知函数f (x )＝ax 2＋1(a >0)，g (x )＝x 3＋bx .(1)若曲线y ＝f (x )与曲线y ＝g (x )在它们的交点(1，c )处具有公共切线，求a ，b 的值；(2)当a 2＝4b 时，求函数f (x )＋g (x )的单调区间，并求其在区间(－∞，－1]上的最大值．解：(1)由(1，c )为公共切点，f (x )＝ax 2＋1(a >0)，则f ′(x )＝2ax ，k 1＝2a ，g (x )＝x 3＋bx ，g ′(x )＝3x 2＋b ，k 2＝3＋b .∴2a ＝3＋b .①又f (1)＝a ＋1，g (1)＝1＋b ，∴a ＋1＝1＋b ，即a ＝b ，代入①式可得Error!(2)∵a 2＝4b ，∴设h (x )＝f (x )＋g (x )＝x 3＋ax 2＋a 2x ＋1.14∴h ′(x )＝3x 2＋2ax ＋a 2.14令h ′(x )＝0，解得x 1＝－，x 2＝－.a2a6∵a >0，∴－<－.a2a 6∴原函数在上单调递增，在上单调递减，在上单调递(－∞，－a2)(－a 2，－a 6)(－a 6，＋∞)增．①当－1≤－，即a ≤2时，最大值为h (－1)＝a －.a 2a 24②当－<－1<－，即2<a <6时，最大值为h＝1.a2a6(－a2)③当－1≥－，即a ≥6时，最大值为h＝1.a6(－a2)综上所述：当a ∈(0,2]时，最大值为h (－1)＝a －；当a ∈(2，＋∞)时，最大值为ha 24＝1.(－a2)。

活页作业(十二) 函数的极值1．函数f (x )的定义域为R ，导函数y ＝f ′(x )的图像如下图所示，则函数f (x )( )A ．无极大值点，有四个极小值点B ．有三个极大值点，两个极小值点C ．有两个极大值点，两个极小值点D ．有四个极大值点，无极小值点解析：设f ′(x )的图像与x 轴的交点坐标从左往右依次为(x 1,0)，(x 2,0)，(x 3,0)，(x 4,0)，则故答案：C2．若x ＝－2与x ＝4是函数f (x )＝x 3＋ax 2＋bx 的两个极值点，则有( ) A ．a ＝－2，b ＝4 B ．a ＝－3，b ＝－24 C ．a ＝1，b ＝3D ．a ＝2，b ＝－4解析：f ′(x )＝3x 2＋2ax ＋b ，依题意有－2和4是方程3x 2＋2ax ＋b ＝0的两个根，所以有－2a 3＝－2＋4，b3＝－2×4，解得a ＝－3，b ＝－24.答案：B3．已知函数y ＝x －ln(1＋x 2)，则y 的极值情况是( ) A ．有极小值B ．有极大值C ．既有极大值又有极小值D ．无极值解析：∵y ＝x －ln(1＋x 2)，∴y ′＝1－2x 1＋x 2＝(x －1)21＋x 2≥0.故函数无极值．答案：D4．设a ∈R ，若函数y ＝e ax ＋3x ，x ∈R 有大于零的极值点，则( )A ．a >－3B ．a <－3C ．a >－13D ．a <－13解析：令y ′＝a e ax ＋3＝0，得e ax ＝－3a .设x 0为大于0的极值点，∴e ax 0＝－3a .∴a <0，ax 0<0.∴0<e ax 0<1，即0<－3a <1.∴a <－3.答案：B5．已知函数y ＝2x 3＋ax 2＋36x －24在x ＝2处有极值，则该函数的一个递增区间为( ) A ．(2,3) B ．(3，＋∞) C ．(2，＋∞)D ．(－∞，3)解析：∵y ＝2x 3＋ax 2＋36x －24， ∴y ′＝6x 2＋2ax ＋36. ∵函数在x ＝2处有极值， ∴当x ＝2时，y ′＝0， ∴6×22＋2a ×2＋36＝0.∴a ＝－15.∴y ＝2x 3－15x 2＋36x －24， y ′＝6x 2－30x ＋36.令y ′＝0，得6x 2－30x ＋36＝0， ∴x 1＝2，x 2＝3.∴当y ′>0时，x <2或x >3.∴函数的递增区间为(－∞，2)和(3，＋∞)． 答案：B6．函数f (x )＝x 3－3x 2，给出下列说法： ①f (x )是增函数，无极值； ②f (x )是减函数，无极值；③f (x )的增区间是(－∞，0]和[2，＋∞)，减区间是[0,2]； ④f (0)＝0是极大值，f (2)＝－4是极小值． 其中正确的序号是________．解析：由已知得f ′(x )＝3x 2－6x ＝3x (x －2)． 令f ′(x )＝0，得x ＝0或x ＝2.当x 变化时，f ′(x )，f (x )变化状态如下表：且f (x )的极值情况是：f (x )极大值＝f (0)＝0，f (x )极小值＝f (2)＝－4，可知③④是正确的．答案：③④7．若函数y ＝－x 3＋6x 2＋m 的极大值等于13，则实数m 等于________．解析：y ′＝－3x 2＋12x .由y ′＝0，得x ＝0或x ＝4.容易得出当x ＝4时函数取得极大值，所以－43＋6×42＋m ＝13.解得m ＝－19.答案：－198．若y ＝kx 3－x 2＋kx －4在R 上无极值，则实数k 的取值范围是________． 解：求导得y ′＝3kx 2－2x ＋k .∵函数在R 上无极值，即y ′≥0或y ′≤0恒成立． ∴Δ≤0.即(－2)2－4k ·3k ≤0，解得k ≥33或k ≤－33. 答案：⎝⎛⎦⎤－∞，－33∪⎣⎡⎭⎫33，＋∞9．求下列函数的极值： (1)f (x )＝x 3－3x 2－9x ＋5； (2)f (x )＝ln xx.解：(1)函数f (x )＝x 3－3x 2－9x ＋5的定义域为R ，且f ′(x )＝3x 2－6x －9.令f ′(x )＝0，则3x 2－6x －9＝0.解得x 1＝－1，x 2＝3.当x 变化时，f ′(x )与f (x )的变化情况如下表：增加减少增加∴x f (3)＝－22.(2)函数f (x )＝ln xx 的定义域为(0，＋∞)，且f ′(x )＝1－ln xx 2，令f ′(x )＝0，得x ＝e.当x 变化时，f ′(x )与f (x )的变化情况如下表：增加减少∴x ＝e 是函数的极大值点，极大值为f (e)＝1e ，没有极小值点．10．已知函数f (x )＝a x 3＋bx 2，当x ＝1时，有极大值3. (1)求a ，b 的值；(2)求函数y ＝f (x )的极小值．解：(1)∵当x ＝1时，函数有极大值3， f ′(x )＝3ax 2＋2bx ，∴⎩⎪⎨⎪⎧ f ′(1)＝0，f (1)＝3.∴⎩⎪⎨⎪⎧3a ＋2b ＝0，a ＋b ＝3.解得a ＝－6，b ＝9.(2)f ′(x )＝－18x 2＋18x ＝－18x (x －1)． 当f ′(x )＝0时，x ＝0或x ＝1； 当f ′(x )>0时，0<x <1； 当f ′(x )<0时，x <0或x >1.∴函数f (x )＝－6x 3＋9x 2的极小值为f (0)＝0.11．设三次函数f (x )的导函数为f ′(x )，函数y ＝xf ′(x )的图像的一部分如下图所示，则正确的是( )A ．f (x )的极大值为f (3)，极小值为f (－3)B ．f (x )的极大值为f (－3)，极小值为f (3)C ．f (x )的极大值为f (－3)，极小值为f (3)D ．f (x )的极大值为f (3)，极小值为f (－3) 解析：由题图可知，当x ∈(－∞，－3)时，xf ′(x )>0，即f ′(x )<0； 当x ∈(－3,0)时，xf ′(x )<0，即f ′(x )>0； 当x ∈(0,3)时，xf ′(x )>0，即f ′(x )>0； 当x ∈(3，＋∞)时，xf ′(x )<0，即f ′(x )<0.故函数f (x )在x ＝－3处取得极小值，在x ＝3处取得极大值． 答案：D12．已知函数y ＝f (x )＝x 3＋3ax 2＋3bx ＋c 在x ＝2处有极值，其图像在x ＝1处的切线平行于直线6x ＋2y ＋5＝0，则f (x )的极大值与极小值之差为________．解析：∵y ′＝3x 2＋6ax ＋3b ，∴⎩⎪⎨⎪⎧ 3×22＋6a ×2＋3b ＝0，3×12＋6a ×1＋3b ＝－3.解得⎩⎪⎨⎪⎧a ＝－1，b ＝0. ∴y ′＝3x 2－6x .令3x 2－6x ＝0，得x ＝0或x ＝2. ∴f (x )极大值－f (x )极小值＝f (0)－f (2)＝4. 答案：413．函数f (x )＝x 3－3ax ＋b (a >0)的极大值为6，极小值为2，则f (x )的单调递减区间是________．解析：令f ′(x )＝3x 2－3a ＝0，得x ＝±a . 则f (x )，f ′(x )随x 的变化情况如下表：∴⎩⎪⎨⎪⎧(－a )3－3a (－a )＋b ＝6，(a )3－3a a ＋b ＝2.解得⎩⎪⎨⎪⎧a ＝1，b ＝4.∴f (x )的递减区间是(－1,1)． 答案：(－1,1)14．如下图是y ＝f (x )导数的图像，对于下列四种说法：①f (x )在[－2，－1]上是增加的； ②x ＝－1是f (x )的极小值点；③f (x )在[－1,2]上是增加的，在[2,4]上是减少的； ④3是f (x )的极小值点． 其中正确的是________．解析：根据导数与函数的单调性、极值之间的关系可判断． 答案：②③15．设函数f (x )＝x 3－3x ＋1. (1)求函数f (x )的单调区间和极值；(2)若关于x 的方程f (x )＝a 有三个不同实根，求实数a 的取值范围． 解：(1)∵f ′(x )＝3x 2－3， 令f ′(x )＝0，则3x 2－3＝0. 解得x 1＝－1，x 2＝1.∴当x <－1或x >1时，f ′(x )>0； 当－1<x <1时，f ′(x )<0.∴f (x )的递增区间为(－∞，－1)和(1，＋∞)； f (x )的递减区间为(－1,1)．当x＝－1时，f(x)有极大值3；当x＝1时，f(x)有极小值－1.(2)由(1)得函数y＝f(x)的图像大致形状如下图所示，当－1<a<3时，直线y＝a与y＝f(x)的图像有三个不同交点．即方程f(x)＝a有三个不同的实根时，a的取值范围为(－1,3)．16．(2014·重庆高考卷)已知函数f(x)＝a e2x－b e－2x－cx(a，b，c∈R)的导函数f′(x)为偶函数，且曲线y＝f(x)在点(0，f(0))处的切线的斜率为4－c.(1)确定a，b的值；(2)若c＝3，判断f(x)的单调性；(3)若f(x)有极值，求c的取值范围．解：(1)对f(x)求导得f′(x)＝2a e2x＋2b e－2x－c，由f′(x)为偶函数，知f′(－x)＝f′(x)，即2(a－b)(e2x－e－2x)＝0，∴a＝b.又f′(0)＝2a＋2b－c＝4－c，∴a＝1，b＝1.(2)当c＝3时，f(x)＝e2x－e－2x－3x，∴f′(x)＝2e2x＋2e－2x－3≥22e2x·2e－2x－3＝1>0.∴f(x)在R上为增函数．(3)由(1)知f′(x)＝2e2x＋2e－2x－c，而2e2x＋2e－2x≥22e2x·2e－2x＝4，当x＝0时等号成立．下面分三种情况进行讨论．当c<4时，对任意x∈R，f′(x)＝2e2x＋2e－2x－c>0，此时f(x)无极值；当c ＝4时，对任意x ≠0， f ′(x )＝2e 2x ＋2e －2x －4>0， 此时f (x )无极值；当c >4时，令e 2x＝t ，方程2t ＋2t －c ＝0有两根t 1＝c －c 2－164>0，t 2＝c ＋c 2－164>0，即f ′(x )＝0有两个根x 1＝12ln t 1，x 2＝12ln t 2.当x 1<x <x 2时f ′(x )<0； 又当x >x 2时，f ′(x )>0.从而f (x )在x ＝x 2处取得极小值．综上，若f (x )有极值，则c 的取值范围为(4，＋∞)．。

第三章 §2 2.11．某人拉动一个物体前进，他所做的功W 是时间t 的函数W ＝W (t )，则W ′(t 0)表示( )A ．t ＝t 0时做的功B ．t ＝t 0时的速度C ．t ＝t 0时的位移D ．t ＝t 0时的功率解析：功率＝做功时间答案：D2．一个物体的运动方程为s ＝1－t ＋t 2(s 的单位是m ，t 的单位是s)，那么物体在3 s 末的瞬时速度是( )A ．7 m/sB ．6 m/sC ．5 m/sD ．4 m/s 解析：s ′＝－1＋2t ，s ′|t ＝3＝－1＋2×3＝5.答案：C3．设球的半径为时间t 的函数R (t )．若球的体积以均匀速度C 增长，则球的表面积的增长速度与球半径( )A ．成正比，比例系数为CB ．成正比，比例系数为2CC ．成反比，比例系数为CD ．成反比，比例系数为2C解析：根据题意，V ＝43πR 3(t )，S ＝4πR 2(t )， 球的体积增长速度为V ′＝4πR 2(t )·R ′(t )，球的表面积增长速度S ′＝2·4πR (t )·R ′(t )， 又∵球的体积以均匀速度C 增长，∴球的表面积的增长速度与球半径成反比，比例系数为2C ．答案：D4．人体血液中药物的质量浓度c ＝f (t )(单位：mg/mL)随时间t (单位：min)变化，且f ′(2)＝0.3，则f ′(2)表示__________.答案：服药后2 min 时血液中药物的质量浓度以每分钟0.3 mg/mL 的速度增加5．物体做自由落体运动，其方程为s (t )＝12gt 2.(其中位移单位：m ，时间单位：s ，g ＝9.8 m/s 2)(1)计算当t 从2 s 变到4 s 时，位移s 关于时间t 的平均变化率，并解释它的意义；(2)求当t ＝2 s 时的瞬时速度，并解释它的意义．解：(1)当t 从2 s 变到4 s 时，位移s 从s (2)变到s (4)，此时，位移s 关于时间t 的平均变化率为s (4)－s (2)4－2＝12g ×42－12g ×224－2＝9.8×3＝29.4(m/s)． 它表示物体从2 s 到4 s 这段时间平均每秒下落29.4 m.(2)∵s ′(t )＝gt ，∴s ′(2)＝2g ＝19.6(m/s)．它表示物体在t ＝2 s 时的速度为19.6 m/s.。

第三章 本章整合提升1．(2016·四川卷)设p ：实数x ，y 满足x ＞1且y ＞1，q ：实数x ，y 满足x ＋y ＞2，则p 是q 的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件解析：⎭⎪⎬⎪⎫当x ＞1，y ＞1时，x ＋y ＞2一定成立，即p ⇒q 当x ＋y ＞2时，可以x ＝－1，y ＝4，即q /⇒p ⇒ p 是q 的充分不必要条件. 答案：A2．(2016·浙江卷)已知函数f (x )满足：f (x )≥|x |且f (x )≥2x ，x ∈R . ( ) A ．若f (a )≤|b |，则a ≤b B ．若f (a )≤2b ，则a ≤b C ．若f (a )≥|b |，则a ≥bD ．若f (a )≥2b ，则a ≥b解析：若f (a )≤2b ，则2a ≤f (a )≤2b .故a ≤b . 答案：B3．(2014·北京卷)学生的语文、数学成绩均被评定为三个等级，依次为“优秀”“合格”“不合格”．若学生甲的语文、数学成绩都不低于学生乙，且其中至少有一门成绩高于乙，则称“学生甲比学生乙成绩好”．如果一组学生中没有哪名学生比另一名学生成绩好，并且不存在语文成绩相同、数学成绩也相同的两名学生，那么这组学生最多有( )A ．2人B ．3人C ．4人D ．5人解析：满足题目条件的最多有3人，其中一个人语文最好，数学最差，另一个人语文最差数学最好，第三个人成绩均为中等．故选B ．答案：B4．(2014·陕西卷)已知f (x )＝x1＋x，x ≥0，若f 1(x )＝f (x )，f n ＋1(x )＝f (f n (x ))，n ∈N ＋，则f 2 014(x )的表达式为________.解析：由f 1(x )＝x 1＋x ⇒f 2(x )＝f ⎝⎛⎭⎫x 1＋x ＝x 1＋x 1＋x 1＋x ＝x1＋2x ；又可得f 3(x )＝f (f 2(x ))＝x 1＋2x 1＋x 1＋2x ＝x 1＋3x ，故可猜想f 2 014(x )＝x1＋2 014x.答案：f 2 014(x )＝x1＋2 014x5．(2014·课标Ⅰ)甲、乙、丙三名同学被问到是否去过A ，B ，C 三个城市时， 甲说：我去过的城市比乙多，但没去过B 城市； 乙说：我没去过C 城市； 丙说：我们三人去过同一城市． 由此可判断乙去过的城市为________.解析：由丙可知，乙至少去过一个城市．由甲、乙可知，甲去过A ，C 且比乙多，且乙没有去过C 城市，故乙只去过A 城市．答案：A6．(2016·四川卷)在平面直角坐标系中，当P (x ，y )不是原点时，定义P 的“伴随点”为P ′⎝⎛⎭⎪⎫y x 2＋y 2，－x x 2＋y 2；当P 是原点时，定义P 的“伴随点”为它自身．现有下列命题：①若点A 的“伴随点”是点A ′，则点A ′的“伴随点”是点A ； ②单位圆上的点的“伴随点”仍在单位圆上；③若两点关于x 轴对称，则它们的“伴随点”关于y 轴对称； ④若三点在同一条直线上，则它们的“伴随点”一定共线． 其中的真命题是________________.(写出所有真命题的序号) 解析：根据定义求解．①设A (2,1)，则其伴随点为A ′⎝⎛⎭⎫15，－25，而A ′的伴随点为(－2，－1)，故①错． ②设P (x ，y )，其中x 2＋y 2＝1，则其伴随点为(y ，－x )，该点也在圆x 2＋y 2＝1上，故②正确．③设A (x ，y )，B (x ，－y )，则它们的伴随点分别为A ′⎝ ⎛⎭⎪⎫y x 2＋y 2，－x x 2＋y 2，B ′⎝⎛⎭⎪⎫－y x 2＋y 2，－x x 2＋y 2，A ′与B ′关于y 轴对称，故③正确．④设共线的三点A (－1,0)，B (0,1)，C (1,2)，则它们的伴随点分别为A ′(0,1)，B ′(1,0)，C ′⎝⎛⎭⎫25，－15，此三点不共线，故④不正确． 答案：②③7．(2016·北京卷)如图，在四棱锥P -ABCD 中，PC ⊥平面ABCD ，AB ∥DC ，DC ⊥AC ．(1)求证：DC ⊥平面P AC ； (2)求证：平面P AB ⊥平面P AC ；(3)设点E 为AB 的中点，在棱PB 上是否存在点F ，使得P A ∥平面CEF ？说明理由． (1)证明：∵PC ⊥平面ABCD ，DC 平面ABCD ， ∴PC ⊥DC ．∵DC ⊥AC ，PC ∩AC ＝C ， ∴DC ⊥平面P AC ．(2)证明：∵AB ∥DC ，DC ⊥AC ， ∴AB ⊥AC ．∵PC ⊥平面ABCD ，AB 平面ABCD ， ∴PC ⊥AB ． ∵PC ∩AC ＝C ， ∴AB ⊥平面P AC ． ∵AB 平面P AB ， ∴平面P AB ⊥平面P AC ．(3)解：在棱PB 上存在中点F ，使得P A ∥平面CEF .∵点E 为AB 的中点，∴EF ∥P A ．∵P A 平面CEF ，EF 平面CEF ， ∴P A ∥平面CEF .8．(2016·四川卷)设函数f (x )＝ax 2－a －ln x ，g (x )＝1x －ee x ，其中a ∈R ，e ＝2.718…为自然对数的底数．(1)讨论f (x )的单调性； (2)证明：当x >1时，g (x )>0；(3)确定a 的所有可能取值，使得f (x )>g (x )在区间(1，＋∞)内恒成立．(1)解：f ′(x )＝2ax －1x ＝2ax 2－1x(x >0)．当a ≤0时，f ′(x )<0，f (x )在(0，＋∞)内单调递减． 当a >0时，由f ′(x )＝0，有x ＝12a. 当x ∈⎝⎛⎭⎫0，12a 时，f ′(x )<0，f (x )单调递减； 当x ∈⎝⎛⎭⎫12a ，＋∞时，f ′(x )>0，f (x )单调递增． (2)证明：令s (x )＝e x －1－x ，则s ′(x )＝e x －1－1. 当x >1时，s ′(x )>0，所以e x －1>x ，从而g (x )＝1x －1ex －1>0.(3)解：由(2)，当x >1时，g (x )>0. 当a ≤0，x >1时，f (x )＝a (x 2－1)－ln x <0.故当f (x )>g (x )在区间(1，＋∞)内恒成立时，必有a >0. 当0<a <12时，12a >1.由(1)有f ⎝⎛⎭⎫12a <f (1)＝0，而g ⎝⎛⎭⎫12a >0， 所以此时f (x )>g (x )在区间(1，＋∞)内不恒成立． 当a ≥12时，令h (x )＝f (x )－g (x )(x ≥1)．当x >1时，h ′(x )＝2ax －1x ＋1x 2－e 1－x>x －1x ＋1x 2－1x ＝x 3－2x ＋1x 2＞x 2－2x ＋1x 2＞0.因此h (x )在区间(1，＋∞)内单调递增．又因为h (1)＝0，所以当x >1时，h (x )＝f (x )－g (x )>0，即f (x )>g (x )恒成立． 综上，a ∈⎣⎡⎭⎫12，＋∞.。

30分钟训练(巩固类训练，可用于课后)1.小明和小刚在课外阅读过程中看到这样一条信息：“肥皂泡厚度为0.000 000 7米.”小明说：“小刚，我用科学记数法来表示肥皂泡的厚度，你能选出正确的一项吗？”小刚给出的答案中正确的是（）A.0.7×10-6B.0.7×10-7C.7×10-7D.7×10-6解析：绝对值小于1的数用科学记数法a×10n表示，其中1≤|a|＜10,n为第一个不为0的数字前面所有0个数的相反数.答案：C2.到2018年末，每百户城镇居民家庭拥有家用汽车5.1×10-1辆，即为_____________辆（）A.52B.5.1C.0.51D.0.181解析：5.1×10-1=5.1×0.1=0.51.答案：C3.下列说法错误的是（）A.近似数0.8与0.80表示的意义不同B.近似数0.200 0精确到万分位C.3.450×118是精确到十位的近似数D.49 554精确到万位是49 000解析：本题主要考查了近似数的精确度以及用四舍五入法按要求取近似值，显然A、B都是正确的.对于C，可考虑到3.450×118中的0在3.450×118的具体数位而定，而它恰好处于十位上，故这个近似数精确到了十位，因而C是正确的.在D中，把49 554精确至万位时，应对千位上数字进行四舍五入，而千位上数字为9，故应向前入一位，因而49 554精确到万位的近似数是5万或5×118.所以D选项是错误的，这恰符合本题的意思.答案：D4.由四舍五入法得到的近似数2.34×10-2，它精确到（）A.百分位B.个位C.千分位D.万分位解析：2.34×10-2=2.34×0.01=0.183 4，故精确到万分位.答案：D5.下列数据中，属于精确数据的有（）①王雨考试得了96分②全班数学测试平均分约为88.2分③小红今天做了5道作业题④珠穆朗玛峰高是8 848米A.1个B.2个C.3个D.4个解析：①③是精确数据.答案：B6.(2018广东毕业，3)据广东信息网消息，2018年第一季度，全省经济运行呈现平稳增长态势，初步核算，全省完成生产总值约为5 218亿元，用科学记数法表示这个数为（）A.5.218×118亿元 B.0.520 6×118亿元C.5.218×118亿元D.0.520 6×118亿元解析：绝对值大于10的数用科学记数法a×10n表示时，1≤|a|＜10，n为整数的位数减去1.520 6亿元=5.218×118亿元.答案：C7.0.000 000 168=1.68×10x,则x=____________.解析：∵0.000 000 168=1.68×10-7,∴x=-7.答案：-78.某地图的比例尺为1∶1 000 000，如果某人在图上量得A 、B 两城距离为1 cm ，请推测A 、B 两城实际距离应为______________cm.（用科学记数法表示）解析：1×1 000 000=1×118 （cm ）.答案：1×1189.一个数是180.446，请按下列要求取这个数的近似数.（1）精确到0.01;（2）精确到0.1;(3)精确到个位；（4）精确到十位.解：用四舍五入法分别按要求取舍.精确到十位时，写成180是错误的，会误认为精确到个位,应表示成1.8×118.可得(1)180.45 (2)180.4 (3)180 (4)1.8×11810.根据图3-1-1中的标识，估计橡皮的长度并写出它的有效数字.图3-1-1（1）精确到0.1 cm;(2)精确到0.01 cm.解：因为接近4cm 至4.5cm 间的第三个刻度，故精确到0.1 cm 为4.3 cm ，精确到0.01 cm 为4.29 cm.故可知（1）4.3 cm;(2)4.29cm.11.体育委员给王磊、赵立两位的身高都记为1.7×118 cm,可有的同学说王磊比赵立高9 cm ，这种情况可能吗？请说明你的理由.解：有这种可能.理由：∵1.65×118≈1.7×118,1.74×118≈1.7×118,∴1.65×118-1.74×118=9 （cm ）,即身高为1.65×118的赵立与身高1.74×118的王磊相差9 cm.12.声音的速度大约是330 m/s ，光的速度大约是3×118 m/s.一架飞机以声音的速度飞行，问用多少小时才能飞过光1秒所经过的距离？（结果保留3位有效数字）解：利用除法运算先求出用的秒数，再化成小时.由题意可得：3×118÷（330×3 600）=6810188.1103⨯⨯≈2.53×118(小时). 答：略。

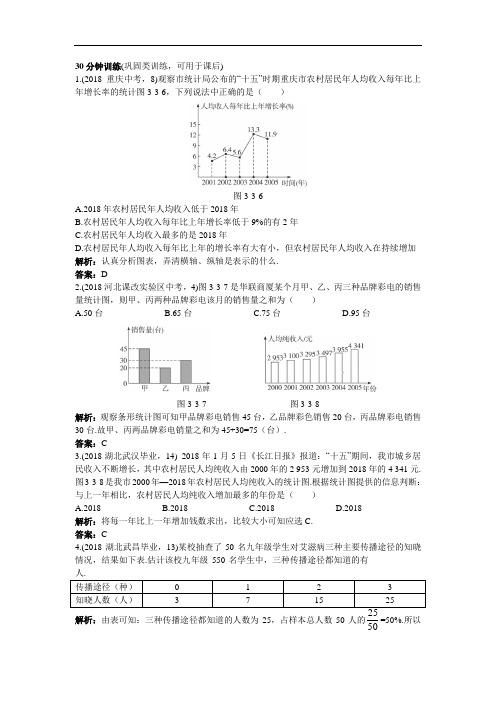
30分钟训练(巩固类训练，可用于课后)1.(2018重庆中考，8)观察市统计局公布的“十五”时期重庆市农村居民年人均收入每年比上年增长率的统计图3-3-6，下列说法中正确的是（）图3-3-6A.2018年农村居民年人均收入低于2018年B.农村居民年人均收入每年比上年增长率低于9%的有2年C.农村居民年人均收入最多的是2018年D.农村居民年人均收入每年比上年的增长率有大有小，但农村居民年人均收入在持续增加解析：认真分析图表，弄清横轴、纵轴是表示的什么.答案：D2.(2018河北课改实验区中考，4)图3-3-7是华联商厦某个月甲、乙、丙三种品牌彩电的销售量统计图，则甲、丙两种品牌彩电该月的销售量之和为（）A.50台B.65台C.75台D.95台图3-3-7 图3-3-8解析：观察条形统计图可知甲品牌彩电销售45台，乙品牌彩色销售20台，丙品牌彩电销售30台.故甲、丙两品牌彩电销量之和为45+30=75（台）.答案：C3.(2018湖北武汉毕业，14) 2018年1月5日《长江日报》报道：“十五”期间，我市城乡居民收入不断增长，其中农村居民人均纯收入由2000年的2 953元增加到2018年的4 341元.图3-3-8是我市2000年—2018年农村居民人均纯收入的统计图.根据统计图提供的信息判断：与上一年相比，农村居民人均纯收入增加最多的年份是（）A.2018B.2018C.2018D.2018解析：将每一年比上一年增加钱数求出，比较大小可知应选C.答案：C4.(2018湖北武昌毕业，13)某校抽查了50名九年级学生对艾滋病三种主要传播途径的知晓情况，结果如下表.估计该校九年级550名学生中，三种传播途径都知道的有____________=50%.所以解析：由表可知：三种传播途径都知道的人数为25，占样本总人数50人的50550名学生中三种传播途径都知道的有550×50%=275（人）.答案：2755.如图3-3-9所示，是世界人口对于不同海拔、不同面积的分布示意图，根据图形提供的信息，完成下列问题.（1）居住在海拔200 m—500 m高度内的人口在总人口数中占的比例是______________. （2）人口密度最大的陆地海拔是______________.（3）居住在海拔1 000 m以上的人口占全世界人口数的比例是______________.图3-3-9 图3-3-10解析：仔细观察所给图，从中获取有关的信息，从而解答出问题.答案：（1）24% （2）0—200 m （3）8.2%6.某校对全校3 000名学生是否在家主动帮助家长干活这一情况进行了问卷调查，供选择的答案是：A.主动帮家长干活 B.有时主动帮家长干活 C.从不主动帮家长干活.将得到的数据通过处理后，画出了如图3-3-10的扇形统计图，请根据这个扇形统计图计算出主动帮家长干活的人数为______________人.解析：3 000×（1-60%-25%）=450（人）.答案：4507.下面四幅图（如图3-3-11）分别是哈尔滨、北京、武汉、广州降水量年变化柱状图.图3-3-11（1）根据图中所提供的信息指出四地降水较多的各是哪几个月？（2）比较四地降水量的年变化有什么共同点，又有什么明显差异？解：（1）哈尔滨降水量较多的是6，7，8，9四个月；北京降水量较多的是6，7，8三个月；武汉降水量较多的是3，4，5，6，7，8六个月；广州降水量较多的是4，5，6，7，8，9六个月.(2)四地年降水量的共同点是：降水量多集中在5月—9月，一般占全年降水量的百分之八十左右，但雨季差别很大，哈尔滨、北京两地雨季开始晚，结束早，雨季短；武汉、广州两地雨季开始早，结束晚，雨季长.8.如图3-3-12是一个反映1996—2018年中国人口变化情况的统计图.1996—2018年中国人口变化趋势图3-3-12（1）从图中你能获得哪些信息？（2）你能预测出2018年中国人口的自然增长率吗？解：（1）可以获得中国从1996—2018年每年的人口总数，中国总人口数从1996年的122 389万人到2018年的128 453万人，人口数逐年增加；人口的自然增长率由1996年的10.42‰下降到2018年的6.45‰，下降趋势明显.(2)预测2018年中国人口的自然增长率不到6‰.（1）从上表中，你能得到什么信息？（2）通过对上表的分析，你有什么想法？解：开放性题目，答案不唯一，只要合理即可，如（1）我国人口在不断增长；1999年我国人口为12.59亿.（2）必须坚持计划生育的基本国策，大力发展教育事业，提高人们的素质.（2）在（1）的统计图中画出第三条表示除中国外的其他国家人口的变化情况；（3）比较三条折线的变化趋势.解：（1）画的图形如图（1）所示：（1）（2）如图（2）所示：（2）（3）从折线上看，世界人口数上升趋势在加快，我国人口总数上升趋势在变慢，其他国家人口总数上升也在加快.。

第三章 本章整合提升一、选择题1．已知变量x 和y 满足关系y ＝－0.1x ＋1，变量y 与z 正相关，则下列结论正确的是( ) A ．x 与y 负相关，x 与z 负相关 B ．x 与y 正相关，x 与z 正相关 C ．x 与y 正相关，x 与z 负相关D ．x 与y 负相关，x 与z 正相关解析：由回归方程知x 与y 负相关，又因为y 与z 正相关，所以x 与z 负相关．故选A ． 答案：A2．(2015·福建卷)为了解某社区居民的家庭年收入与年支出的关系，随机调查了该社区5户家庭，得到如下统计数据表：根据上表可得回归直线方程y ^＝b ^x ＋a ^，其中b ^＝0.76，a ^＝y －b ^x .据此估计，该社区一户年收入为15万元家庭的年支出为( )A ．11.4万元B ．11.8万元C ．12.0万元D ．12.2万元解析：回归直线一定过样本中心(10,8)，∵b ^＝0.76，∴a ^＝0.4.由y ^＝0.76x ＋0.4得当x ＝15万元时，y ^＝11.8万元，故选B ． 答案：B3．设某大学的女生体重y (单位：kg)与身高x (单位：cm)具有线性相关关系．根据一组样本数据(x i ，y i )(i ＝1,2，…，n )，用最小二乘法建立的回归方程为y ＝0.85x －85.71，则下列结论不正确的是( )A ．y 与x 具有正的线性相关关系B ．回归直线过样本点的中心(x －，y －)C ．若该大学某女生身高增加1 cm ，则其体重约增加0.85 kgD ．若该大学某女生身高为170 cm ，则可断定其体重必为58.79 kg解析：当x ＝170时，y ＝0.85×170－85.71＝58.79，体重的估计值为58.79 kg ，故D 不正确．答案：D4．已知x 与y 之间的几组数据如下表：假设根据上表数据所得线性回归方程为y ＝bx ＋a .若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y ＝b ′x ＋a ′，则以下结论正确的是( )A ．b ＞b ′，a ＞a ′B ．b ＞b ′，a ＜a ′C ．b ＜b ′，a ＞a ′D ．b ＜b ′，a ＜a ′解析：由两组数据(1,0)和(2,2)可求得直线方程为y ＝2x －2，b ′＝2，a ′＝－2.而利用线性回归方程的公式与已知表格中的数据，可求得b ＝∑i ＝16x i y i －6x ·y∑i ＝16x 2i －6x －2＝58－6×72×13691－6×⎝⎛⎭⎫722＝57，a ＝y －b x －＝136－57×72＝－13，所以b ＜b ′，a ＞a ′．答案：C 二、填空题5．有同学在用电子邮件时发现了一个有趣的现象，中国人的邮箱名称里含有数字的比较多，而外国人的邮箱名称里含有数字的比较少，为了研究国籍与邮箱名称是否含有数字有关，于是我们共收集了124个邮箱名称，其中中国人的64个，外国人的60个，中国人的邮箱名称中有43个含数字，外国人的邮箱名称中有27个含数字．那么认为“国籍和邮箱名称里是否含有数字有关”的把握性为________．(用百分数表示)．附：χ2＝n (ad －bc )2(a ＋b )(c ＋d )(a ＋c )(b ＋d ).由表中数据，得χ2＝124×(43×33－27×21)270×54×64×60≈6.201．∵χ2≥5.024，∴有97.5%的把握认为“国籍和邮箱名称里是否含有数字有关”． 答案：97.5%6．已知x ，y 的取值如下表：从散点图分析，y 与x 则实数a 的值为________． 解析：x ＝2＋3＋4＋54＝3. 5，y ＝2.2＋3.8＋5.5＋6.54＝4.5，回归直线必过样本的中心点(x ，y )，把(3.5，4.5)代入回归方程，计算得a ＝－0.61．答案：－0.617．调查者通过随机询问72名男女生喜欢文科还是理科，得到如下列联表(单位：名)： 性别与喜欢文科还是理科列联表学生的性别和喜欢文科还是理科________关系．(填“有”或“没有”) 附：当χ2＞7.879时，有99.5%以上的把握判定变量A ，B 有关联． 解析：通过计算χ2＝72×(8×16－28×20)236×36×28×44≈8.42＞7.879．故我们有99.5%的把握认为学生的性别和喜欢文科还是理科有关系． 答案：有 三、解答题8．某火锅店为了解气温对营业额的影响，随机记录了该店1月份中5天的日营业额y (单位：千元)与该地当日最低气温x (单位：℃)的数据，如下表：(1)求y 关于x (2)判定y 与x 之间是正相关还是负相关；若该地1月份某天的最低气温为6 ℃，用所求回归方程预测该店当日的营业额．附：回归方程y ＝bx ＋a 中，b ＝∑i ＝1nx i y i －n x － y－∑i ＝1nx 2i －n x2，a ＝y －b x ．解：(1)列表.这里n ＝5，x ＝1n ∑i ＝1n x i ＝355＝7，y ＝1n ∑i ＝1n y i ＝455＝9．又l xx ＝∑i ＝1nx 2i －n x 2＝295－5×72＝50，l xy ＝∑i ＝1nx i y i －n x －y －＝287－5×7×9＝－28，从而，b ＝l xy l xx ＝－2850＝－0.56，a ＝y －b x ＝9－(－0.56)×7＝12.92， 故所求回归方程为y ＝－0.56x ＋12.92． (2)由b ＝－0.56<0知y 与x 之间是负相关． 将x ＝6代入回归方程可预测该店当日的营业额为 y ＝－0.56×6＋12.92＝9.56(千元)．9．心理学家分析发现视觉和空间能力与性别有关，某数学兴趣小组为了验证这个结论，从兴趣小组中按分层抽样的方法抽取50名同学(男30，女20)，给所有同学几何题和代数题各一题，让各位同学自由选择一道题进行解答．选题情况如下表(单位：人)：(1)能否据此判断有97.5%的把握认为视觉和空间能力与性别有关？ 附：当χ2＞5.024时，有97.5%以上的把握判定变量A ，B 有关联．(2)经过多次测试后，甲每次解答一道几何题所用的时间在5～7 min ，乙每次解答一道几何题所用的时间在6～8 min ，现甲、乙各解同一道几何题，求乙比甲先解答完的概率．解：(1)由表中数据得χ2＝50×(22×12－8×8)230×20×30×20＝509≈5.556＞5.024，所以根据统计有97.5%的把握认为视觉和空间能力与性别有关． (2)设甲、乙解答一道几何题的时间分别为x min ，y min ，则基本事件满足的区域为⎩⎪⎨⎪⎧5≤x ≤7，6≤y ≤8(如图所示)．设事件A 为“乙比甲先做完此道题”， 则满足的区域为x >y ， 所以P (A )＝12×1×12×2＝18，即乙比甲先解答完的概率为18．。

第三章 §2 2.21．函数y ＝f (x )在[a ， b ]上( )A ．极大值一定比极小值大B ．极大值一定是最大值C ．最大值一定是极大值D ．最大值一定大于极小值解析：由函数的最值与极值的概念可知，y ＝f (x )在[a ，b ]上的最大值一定大于极小值． 答案：D2．函数f (x )＝x 3－3x (|x |<1)( )A ．有最大值，但无最小值B ．有最大值，也有最小值C ．无最大值，但有最小值D ．既无最大值，也无最小值解析：f ′(x )＝3x 2－3＝3(x ＋1)(x －1)，当x ∈(－1,1)时，f ′(x )<0.∴f (x )在(－1,1)上是单调递减函数，无最大值和最小值．答案：D3．函数y ＝ln x x的最大值为( ) A ．e －1 B ．eC ．e 2D ．103 解析：令y ′＝(ln x )′x －ln x ·x ′x 2＝1－ln x x 2＝0. 解得x ＝e.当x >e 时，y ′<0；当x <e 时，y ′>0.y 极大值＝f (e)＝1e，在定义域内只有一个极值， 所以y max ＝1e. 答案：A4．函数f (x )＝3x ＋sin x 在x ∈[0，π]上的最小值为___________．解析：∵f (x )＝3x ＋sin x ，∴f ′(x )＝3x ln 3＋cos x .∵当x ∈[0，π]时，3x ln 3＞1，－1≤cos x ≤1，∴f ′(x )＞0.∴f (x )在[0，π]上单调递增．∴f (x )min ＝f (0)＝1.答案：15．如下图所示，设铁路AB ＝50， B ，C 之间距离为10，现将货物从A 运往C ，已知单位距离铁路费用为2，公路费用为4，问在AB 上何处修筑公路至C ，可使运费由A 至C 最省．解：设M 为AB 上的一点，且MB ＝x ，于是AM 上的运费为2(50－x )，MC 上的运费为4102＋x 2，则由A 到C 的总运费为p (x )＝2(50－x )＋4 100＋x 2(0≤x ≤50)，p ′(x )＝－2＋4x100＋x2. 令p ′(x )＝0，解得 x 1＝1033 ，x 2＝－1033(舍去)． 当x <1033时，p ′(x )<0； 当x >1033时，p ′(x )>0. ∴当x ＝1033时，p (x )取得最小值． 即当在离点B 距离为1033的点M 处修筑公路至C 时，运费最省．。

第三章 §1 1.21．函数f (x )＝1＋3x －x 3有( ) A ．极小值－1，极大值1 B ．极小值－2，极大值3 C ．极小值－2，极大值2 D ．极小值－1，极大值3解析：f ′(x )＝－3x 2＋3， 令f ′(x )＝0，即－3x 2＋3＝0，解得x 1＝－1，x 2＝1. 当x <－1时，f ′(x )<0，f (x )是减少的； 当－1<x <1时，f ′(x )>0，f (x )是增加的； 当x >1时，f ′(x )<0，f (x )是减少的．∴函数的极小值为f (－1)＝1－3＋1＝－1，函数的极大值为f (1)＝1＋3－1＝3. 答案：D2．函数y ＝x 3＋1的极大值是( ) A ．1 B ．0 C ．2D ．不存在解析：y ′＝3x 2≥0，所以函数y ＝x 3＋1在R 上单调递增，故无极大值． 答案：D3．函数f (x )＝x 3＋ax 2＋3x －9，已知f (x )在x ＝－3处取得极值，则a ＝( ) A ．2 B ．3 C ．4D ．5解析：f ′(x )＝3x 2＋2ax ＋3，由f (x )在x ＝－3处取得极值，知f ′(－3)＝0，解得a ＝5. 答案：D4．在下列四个函数中，存在极值的是________． ①y ＝1x②y ＝x 2＋1 ③y ＝2 ④y ＝x 3解析：∵y ′＝－1x 2<0，∴y ＝1x 在定义域内不存在极值．同理，③④也不存在极值．②中，y ′＝2x ，令y ′＝0，得x ＝0.∴当x >0时，y ′>0；当x <0时，y ′<0.故函数y ＝x 2＋1在x ＝0处取极小值．答案：②5．设函数f(x)＝x3＋bx2＋cx(x∈R)，已知g(x)＝f(x)－f′(x)是奇函数．(1)求b，c的值；(2)求g(x)的极值．解：(1)∵f′(x)＝3x2＋2bx＋c，∴g(x)＝f(x)－f′(x)＝x3＋(b－3)x2＋(c－2b)x－c.又g(x)是R上的奇函数，∴g(－x)＝－g(x)．∴(－x)3＋(b－3)x2－(c－2b)x－c＝－x3－(b－3)x2－(c－2b)x＋c.化简，得(b－3)x2－c＝0.∴b＝3，c＝0.(2)由(1)知g(x)＝x3－6x，∴g′(x)＝3x2－6＝3(x＋2)(x－2)．当x变化时，g′(x)，g(x)的变化情况如下表：－2)(2－2，2) (x)在x＝－2处取得极大值为g(－2)＝(－2)3－6×(－2)＝42，在x＝2处取得极小值为g(2)＝(2)3－62＝－4 2.。

活页作业(十一) 导数与函数的单调性(第二课时)1．函数f (x )＝2x 3＋ax 2＋1(a 为常数)在区间(－∞，0)和(2，＋∞)内单调递增，且在区间(0,2)内单调递减，则a 值为( )A ．1B ．2C ．－6D ．－12解析：f ′(x )＝6x 2＋2ax ，依题意得f ′(2)＝24＋4a ＝0，∴a ＝－6. 答案：C2．若函数f (x )＝13x 3＋x 2－ax 在区间(1，＋∞)上是增加的，且在区间(1,2)上有零点，则实数a 的取值范围是( )A ．⎝⎛⎭⎫43，3B ． ⎝⎛⎭⎫43，103 C ．⎝⎛⎦⎤43，3D ．(－∞，3]解析：∵函数f (x )＝13x 3＋x 2－ax 在区间(1，＋∞)上是增加的，∴f ′(x )＝x 2＋2x －a ≥0在区间(1，＋∞)上恒成立． ∴a ≤x 2＋2x ，x ∈(1，＋∞)恒成立． ∵当x >1时，x 2＋2x >3， ∴a ≤3.①∵函数f (x )＝13x 3＋x 2－ax 在区间(1，＋∞)上是增加的，且在区间(1,2)上有零点，∴f (1)<0，f (2)>0. ∴43<a <103.② 由①②得，43<a ≤3.答案：C3．已知f (x )＝⎩⎪⎨⎪⎧x 2(x ≥0)，x 3－(a －1)x ＋a 2－3a －4(x <0) 在(－∞，＋∞)上是增函数，则实数a 的取值范围是( ) A ．(－∞，1] B ．[－1,1] C ．(－∞，1)D ．[－1,4]解析：若原函数在R 上为增函数，则当x <0时，f ′(x )＝3x 2－(a －1)≥0恒成立．因此有a ≤1.还需注意函数在分段点处函数值的大小，应有a 2－3a －4≤0，解得－1≤a ≤4.综上－1≤a ≤1.答案：B4．已知定义在R 上的偶函数f (x )满足x ∈(－∞，0)时，f (x )＋xf ′(x )<0成立，若a ＝20.2f (20.2)，b ＝ln 2·f (ln 2)，c ＝log 0.50.25·f (log 0.50.25)，则a ，b ，c 的大小关系是( )A ．a >b >cB ．c >a >bC ．b >a >cD ．a >c >b解析：构造函数h (x )＝xf (x )，由函数y ＝f (x )是R 上的偶函数，函数y ＝x 是R 上的奇函数，可得h (x )＝xf (x )是R 上的奇函数．又当x ∈(－∞，0)时，h ′(x )＝f (x )＋xf ′(x )<0. ∴函数h (x )在x ∈(－∞，0)上为单调递减函数． ∴h (x )在x ∈(0，＋∞)上为单调递减函数． ∵2>20.2>1,0<ln 2<1，log 0.50.25＝2， ∴log 0.50.25>20.2>ln 2.∴b >a >c . 答案：C5．设p ：f (x )＝x 3＋2x 2＋mx ＋1在(－∞，＋∞)内单调递增，q ：m ≥43，则p 是q 的________条件．( )A ．充要B ．充分不必要C ．必要不充分D ．既不充分又不必要解析：对于p ，由题意知f ′(x )＝3x 2＋4x ＋m ≥0在R 上恒成立，即Δ≤0. ∴4－3m ≤0.∴m ≥43.又当m ＝43时，f (x )＝x 3＋2x 2＋43x ＋1＝⎝⎛⎭⎫x ＋233＋1927在R 上单调递增，∴m ≥43.∴p 是q 的充要条件．答案：A6．若函数f (x )＝x 3＋bx 2＋cx ＋d 的递减区间为[－1， 2]，则b ＝________，c ＝________. 解析：由题意知，f ′(x )＝3x 2＋2bx ＋c ≤0在[－1,2]上恒成立，所以－1,2为方程3x 2＋2bx ＋c ＝0的两根，则b ＝－32，c ＝－6.答案：－32－67．若函数f (x )＝ax 3＋x 恰有三个单调区间，则实数a 的取值范围是________． 解析：∵f ′(x )＝3ax 2＋1，f (x )有三个单调区间， ∴方程3ax 2＋1＝0有两个不等实根． ∴Δ＝0－4×3a ×1>0.解得a <0.答案：(－∞，0)8．已知函数f (x )＝x 3－ax 在[1，＋∞)上是单调递增函数，则a 的最大值是________． 解析：由题意得f ′(x )＝3x 2－a ≥0在[1，＋∞)上恒成立，因此a ≤3.故a 的最大值为3.答案：39．已知函数f (x )＝ln x ，g (x )＝ax (a >0)，设F (x )＝f (x )＋g (x )．(1)求F (x )的单调区间；(2)若以y ＝F (x )(x ∈(0,3])图像上任意一点P (x 0，y 0)为切点的切线的斜率k ≤12恒成立，求实数a 的最小值．解：(1)F (x )＝f (x )＋g (x )＝ln x ＋ax (x >0)，F ′(x )＝1x －a x 2＝x －ax2(x >0)．∵a >0，由F ′(x )>0得x ∈(a ，＋∞)， ∴F (x )在(a ，＋∞)上是增加的． 由F ′(x )<0得x ∈(0，a )， ∴F (x )在(0，a )上是减少的．∴F (x )的递减区间为(0，a )，递增区间为(a ，＋∞)． (2)∵F ′(x )＝x －ax2(0<x ≤3)，∴k ＝F ′(x 0)＝x 0－a x 20≤12(0<x 0≤3)恒成立．即a ≥⎝⎛⎭⎫－12x 20＋x 0max .当x 0＝1时，－12x 20＋x 0取得最大值12， ∴a ≥12.∴a min ＝12.10．设f (x )＝－13x 3＋12x 2＋2ax .若f (x )在⎝⎛⎭⎫23，＋∞上存在单调递增区间，求a 的取值范围． 解：f ′(x )＝－x 2＋x ＋2a ＝－⎝⎛⎭⎫x －122＋14＋2a ， 当x ∈⎣⎡⎭⎫23，＋∞时，f ′(x )的最大值为f ′⎝⎛⎭⎫23＝29＋2a . 函数有单调递增区间，即在⎝⎛⎭⎫23，＋∞内，导函数大于0有解，令29＋2a >0，得a >－19. 所以当a ∈⎝⎛⎭⎫－19，＋∞时，f (x )在⎝⎛⎭⎫23，＋∞上存在单调递增区间．11．已知函数f (x )(x ∈R )满足f (1)＝1，且f (x )的导函数f ′(x )<12，则f (x )<x 2＋12的解集为( )A ．{x |－1<x <1}B ．{x |x <－1}C ．{x |x <－1或x >1}D ．{x |x >1}解析：设g (x )＝f (x )－x 2－12，则g ′(x )＝f ′(x )－12<0.∴g (x )在R 上是减函数．∵g (1)＝f (1)－12－12＝1－1＝0，∴g (x )＝f (x )－x 2－12<0的解集为{x |x >1}．答案：D12．已知函数f (x )＝2e x －mx (其中e ≈2.718…)在区间[－1,0]上单调递减，则实数m 的取值范围为________．解析：由题意得f ′(x )＝2e x －m ≤0在[－1,0]上恒成立，即m ≥2e x 恒成立，可得m ≥2. 答案：[2，＋∞)13．若函数f (x )＝x 3－3ax 2－bx ，其中a ，b 为实数，f (x )在区间[－1,2]上为减函数，且b ＝9a ，则a 的取值范围是________．解析：由已知得f ′(x )＝3x 2－6ax －b ≤0对∀x ∈[－1，2]恒成立， ∵b ＝9a ，∴x 2－2ax －3a ≤0.∵2x ＋3>0. ∴a ≥x 22x ＋3对x ∈[－1,2]恒成立．解得a ≥1. 答案：[1，＋∞)14．已知函数f (x )＝ax －ln x ，若f (x )>1在区间(1，＋∞)内恒成立，则实数a 的取值范围为_________．解析：由已知a >1＋ln xx 在区间(1，＋∞)内恒成立．设g (x )＝1＋ln xx ，∴g ′(x )＝－ln xx2<0(x >1)．∴g (x )＝1＋ln xx 在区间(1，＋∞)内递减．∴g (x )<g (1)． ∵g (1)＝1，∴1＋ln xx<1在区间(1，＋∞)内恒成立．∴a ≥1. 答案：[1，＋∞)15．已知函数f (x )＝a ln x ＋x 3(a 为常数)．(1)若a ＝－3，判断函数f (x )在(1，＋∞)上的单调性； (2)函数f (x )在[1，e]上单调递减，求实数a 的取值范围；(3)若存在x ∈[1，e]，使得f (x )≥ax ＋x 3－x 2＋2x 成立，求实数a 的取值范围．解：(1)当a ＝－3时f ′(x )＝3x 2－3x ＝3(x 3－1)x.当x ∈(1，＋∞)时，f ′(x )>0. ∴函数f (x )在(1，＋∞)上是增函数．(2)由已知得f ′(x )＝a x ＋3x 2＝3x 3＋a x.∵f (x )在[1，e]上单调递减，∴f ′(x )≤0在[1，e]上恒成立．即a ≤－3x 3在[1，e]上恒成立． ∵(－3x 3)min ＝－3e 3，∴a ≤－3e 3. (3)不等式f (x )≥ax ＋x 3－x 2＋2x 可化为 a (x －ln x )≤x 2－2x .∵x ∈[1，e]，∴ln x ≤1≤x ，且不能同时取等号． ∴ln x <x ，即x －ln x >0. ∴a ≤x 2－2xx －ln x (x ∈[1，e])．令g (x )＝x 2－2xx －ln x (x ∈[1，e])，则g ′(x )＝(x －1)(x ＋2－2ln x )(x －ln x )2.当x ∈[1，e]时，x －1≥0，ln x ≤1，x ＋2－2ln x >0，从而g ′(x )≥0(仅当x ＝1时取等号)， ∴g (x )在[1，e]上为增函数． ∴g (x )的最小值为g (1)＝－1. ∴实数a 的取值范围是(－∞，－1]． 16．设函数f (x )＝1＋x 1－xe －ax .(1)试写出定义域及f ′(x )的解析式； (2)设a >0，讨论函数y ＝f (x )的单调性． 解：(1)f (x )的定义域为(－∞，1)∪(1，＋∞)， f ′(x )＝ax 2＋2－a (1－x )2e －ax，其中x ≠1.(2)①当0<a ≤2时，f ′(x )≥0且仅在有限个点处取等号，∴f (x )在(－∞，1)，(1，＋∞)上为增函数．②当a >2时，由f ′(x )>0得ax 2＋2－a >0，解得x >a －2a或x <－a －2a；由f ′(x )<0得ax 2＋2－a <0，解得－a －2a<x < a －2a. 综上所述，当0<a ≤2时，函数y ＝f (x )在(－∞，1)，(1，＋∞)上单调递增；当a >2时，函数y ＝f (x )在⎝ ⎛⎭⎪⎫－∞，－a －2a ，⎝ ⎛⎭⎪⎫a －2a ，1，(1，＋∞)上单调递增，在⎝⎛⎭⎪⎫－a －2a ， a －2a 上单调递减．。