双曲函数表
- 格式:pdf
- 大小:42.49 KB
- 文档页数:1
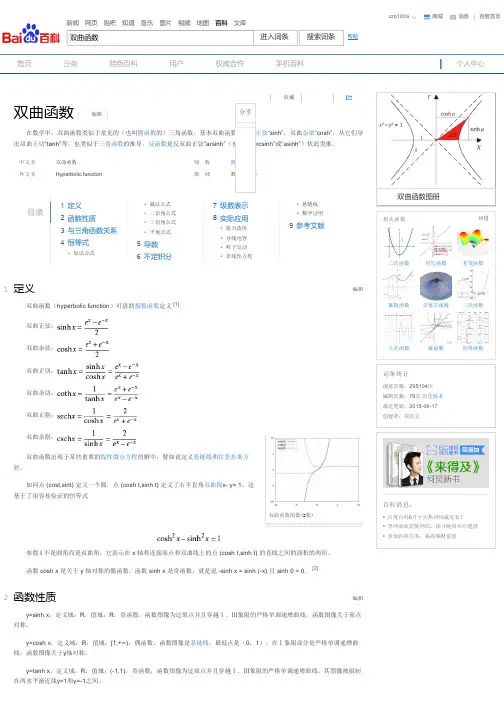


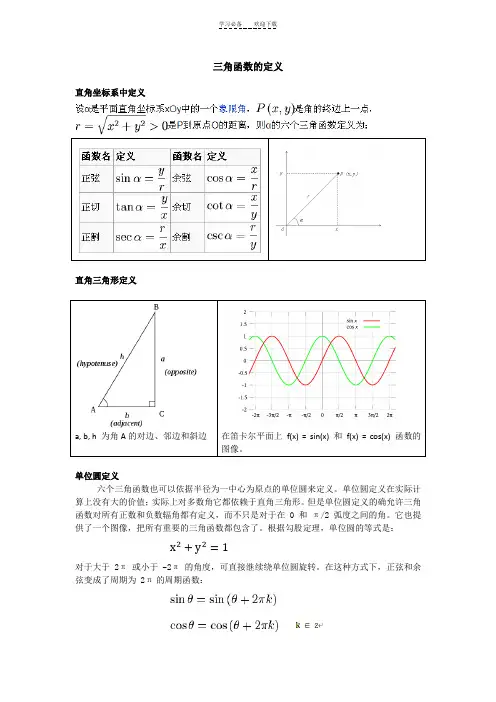
三角函数的定义直角坐标系中定义直角三角形定义a, b, h 为角A的对边、邻边和斜边在笛卡尔平面上f(x) = sin(x) 和f(x) = cos(x) 函数的图像。
单位圆定义六个三角函数也可以依据半径为一中心为原点的单位圆来定义。
单位圆定义在实际计算上没有大的价值;实际上对多数角它都依赖于直角三角形。
但是单位圆定义的确允许三角函数对所有正数和负数辐角都有定义,而不只是对于在 0 和π/2 弧度之间的角。
它也提供了一个图像,把所有重要的三角函数都包含了。
根据勾股定理,单位圆的等式是:对于大于 2π或小于−2π的角度,可直接继续绕单位圆旋转。
在这种方式下,正弦和余弦变成了周期为 2π的周期函数:级数定义只使用几何和极限的性质,可以证明正弦的导数是余弦,余弦的导数是负的正弦。
(在微积分中,所有角度都以弧度来度量)。
我们可以接着使用泰勒级数的理论来证明下列恒等式对于所有实数x都成立:这些恒等式经常被用做正弦和余弦函数的定义。
它们经常被用做三角函数的严格处理和应用的起点(比如,在傅立叶级数中),因为无穷级数的理论可从实数系的基础上发展而来,不需要任何几何方面的考虑。
这样,这些函数的可微性和连续性便可以单独从级数定义来确立。
在这种形式的表达中,分母是相应的阶乘,分子称为“正切数”,它有一个组合解释:它们枚举了奇数势的有限集合的交错排列(alternating permutation)。
在这种形式的表达中,分母是对应的阶乘,而分子叫做“正割数”,有组合解释:它们枚举偶数势的有限集合的交错排列。
从复分析的一个定理得出,这个实函数到复数有一个唯一的解析扩展。
它们有同样的泰勒级数,所以复数上的三角函数是使用上述泰勒级数来定义的。
与指数函数和复数的联系可以从上述的级数定义证明正弦和余弦函数分别是复指数函数在它的自变量为纯虚数时候的虚数和实数部分:这个联系首先由欧拉注意到,叫做欧拉公式。
在这种方式下,三角函数在复分析的几何解释中变成了本质性的。

双曲函数知识点总结双曲函数的定义域是实数集,而值域是实数,它们的定义如下:双曲正弦函数sinh(x) = (e^x - e^(-x)) / 2双曲余弦函数cosh(x) = (e^x + e^(-x)) / 2双曲正切函数tanh(x) = sinh(x) / cosh(x) = (e^x - e^(-x)) / (e^x + e^(-x))双曲函数和普通的三角函数在函数定义和性质上有一些类似,但也有很多不同之处。
接下来我们将重点介绍双曲函数的性质、导数和积分等知识点。
一、双曲函数的性质1. 双曲函数的奇偶性双曲正弦函数sinh(x)是奇函数,即sinh(-x) = -sinh(x)双曲余弦函数cosh(x)是偶函数,即cosh(-x) = cosh(x)2. 双曲函数的增减性双曲正弦函数sinh(x)和双曲余弦函数cosh(x)都是增函数3. 双曲函数的双曲恒等式双曲恒等式是指双曲函数之间的一些关系式,例如:cosh^2(x) - sinh^2(x) = 1tanh(x) = sinh(x) / cosh(x) = (e^x - e^(-x)) / (e^x + e^(-x))二、双曲函数的导数双曲函数的导数也是双曲函数,具体如下:sinh'(x) = cosh(x)cosh'(x) = sinh(x)tanh'(x) = 1 / cosh^2(x)三、双曲函数的积分双曲函数的积分也是双曲函数,具体如下:∫cosh(x)dx = sinh(x) + C∫sinh(x)dx = cosh(x) + C∫tanh(x)dx = ln|cosh(x)| + C在实际的数学问题中,双曲函数的应用非常广泛,特别是在微积分中的积分计算和微分方程的求解中起到重要作用。
同时,双曲函数也在工程、物理、经济学等应用领域中发挥着重要的作用。
总之,双曲函数在数学中起着重要的作用,它们的定义和性质与普通函数有一些相似之处,但也有很多不同之处。

双曲函数和差公式
双曲函数是一类与三角函数类似的数学函数,它们在数学、物理学和工程学中有广泛的应用。
双曲函数包括双曲正弦函数(sinh)、双曲余弦函数(cosh)、双曲正切函数(tanh)等。
差公式是指双曲函数的一种重要性质,它可以用来计算双曲函数的和、差等运算。
双曲函数的差公式可用以下公式表示:cosh(x + y) = cosh(x) * cosh(y) + sinh(x) * sinh(y)
sinh(x + y) = sinh(x) * cosh(y) + cosh(x) * sinh(y)
tanh(x + y) = (tanh(x) + tanh(y)) / (1 + tanh(x) *
tanh(y))
双曲函数的差公式在计算中起到了重要的作用,特别是在处理双曲函数的和、差等运算时,能够简化计算过程,并且可以降低计算误差。
除了差公式,双曲函数还有很多其他的数学性质和公式,例如导
数公式、积分公式等。
双曲函数还与指数函数、对数函数、幂函数等
有一些特殊的关系,可以通过这些关系进行更深入的数学研究和应用。
双曲函数在物理学和工程学中有广泛的应用,例如在电磁学中描
述电场和磁场的分布、在振动学中描述弹性体的振动等。
双曲函数还
与概率论、统计学、信号处理等有密切的联系。
总之,双曲函数和差公式是数学中重要的概念和工具,通过它们
可以描述和计算多种数学问题,具有广泛的应用价值。

探究双曲函数PB07210142,梁海波双曲函数是我们在大学时期微积分课程中新接触的东东,但仿佛仅在《高等数学导论》第一章有所提及,貌似与后来知识没有关系。
本人在做题时发现,双曲函数与后来的微积分,特别是积分求解有许多联系。
首先,我们先认识下双曲函数。
双曲正弦:2xx e e shx --=双曲余弦: 2xx e e chx -+=双曲正切: x x xx e e e e thx --+-= 双曲函数与三角函数有很多相似的性质,在求解积分的过程中,三角函数与双曲函数地位相当,下面对其相似之处进行比较,由于三角函数性质在以前接触较多,这里不在赘述.chx shx thx =chxshy shxchy y x sh ±=±)(shxshy chxchy y x ch ±=±)(122=-x sh x chx ch x sh x ch 222=+shx x sh -=-)(chx x ch =-)(shxchx x sh 22=下面说反双曲函数。
以下记法与书上不同,这样写便于与反三角函数想对比。
)1ln(2-+±=x x arcchx)1ln(2++=x x arcshx)11ln(21xx arcthx -+= 求解积分的问题中,有很多式子含有12-x ,12+x 以及它的倒数与根式形。
书后的简明积分表也给出了相关的公式,但这些公式复杂难记,没能把握住其与双曲函数的内在关系。
我们在解这类问题时往往会采用换元法,令x=sint 或x=sht 等。
其实这样设的目的就是利用了反三角函数,反双曲函数的微分,下面对这些公式作一定的改写。
(1)dx x ⎰+211=c x +arctanc arcthx dx x +=-⎰211 (2)||112arcchx dx x =-⎰c x dx x +=-⎰arcsin 112 c x dx x +=--⎰arccos 112 c arcshx dx x +=+⎰112 (3)2212arcsin 211x x x dx x -+=-⎰ 2212211x x arcshx dx x ++=+⎰ 12||21122-+-=-⎰x x arcchx dx x从形式上简化,实质是从思想上的简化,这样去理解公式不仅便于记忆,更加深了我们对双曲函数的理解。

圆函数(三角函数)1.基本性质:sin tan cos x x x =,cos cot sin xx x = 1sec cos x x =,1csc sin x x =tan cot 1x x =sin csc 1x x = sec cos 1x x =22sin cos 1x x +=221tan sec x x +=,221cot csc x x +=2.奇偶性:sin()sin x x -=- cos()cos x x -= tan()tan x x -=-3.两角和差公式sin()sin cos cos sin x y x y x y ±=± cos()cos cos sin sin x y x y x y ±=m tan tan tan()1tan tan x yx y x y±±=m4.二倍角公式 sin 22sin cos x x x =2222cos 2cos sin 2cos 112sin x x xx x=-=-=-22tan tan 21tan xx x=-双曲函数1.基本性质:sh th ch x x x =,ch cth sh xx x= 1sech ch x x =,1csch sh x x =th cth 1x x = sh csch 1x x = sech ch 1x x =22ch sh 1x x -=221th sech x x -=,221cth csch x x -=-2.奇偶性:sh()sh x x -=- ch()ch x x -= th()th x x -=-3.两角和差公式sh()sh ch ch sh x y x y x y ±=± ch()ch ch sh sh x y x y x y ±=± th th th()1th th x yx y x y±±=±4.二倍角公式 sh 22sh ch x x x =2222ch 2ch +sh 2ch 112sh x x xx x==-=+ 22th th 21th xx x=+5.半角公式 21cos sin 22x x -=,21cos cos 22x x += sin 1cos tan 21cos sin x x xx x-==+ 21cos 2sin 2x x -=,21cos 2cos 2x x +=6.万能公式22tan2sin 1tan 2xx x=+,221tan 2cos 1tan 2x x x -=+ 22tan2tan 1tan 2x x x=-7.三倍角公式3sin33sin 4sin x x x =-3cos34cos 3cos x x x =-8.积化和差公式()()1sin cos sin sin 2x y x y x y =++-⎡⎤⎣⎦()()1cos sin sin sin 2x y x y x y =+--⎡⎤⎣⎦ ()()1cos cos cos cos 2x y x y x y =++-⎡⎤⎣⎦()()1sin sin cos cos 2x y x y x y =-+--⎡⎤⎣⎦9.和差化积公式sin sin 2sin cos 22x y x yx y +-+=sin sin 2cos sin22x y x yx y +--=cos cos 2cos cos22x y x yx y +-+=cos cos 2sin sin22x y x yx y +--=- 5.半角公式2ch 1sh 22x x -=,2ch 1ch 22x x +=sh ch 1th 2ch 1sh x x x x x-==+2ch 12sh 2x x -=,2ch 12ch 2x x +=6.万能公式22th2sh 1th 2xx x =-,221th 2cos 1th 2x x x +=- 22th2th 1th 2x x x =+7.三倍角公式3sh 33sh 4sh x x x =+ 3ch34ch 3ch x x x =-8.积化和差公式()()1sh ch sh sh 2x y x y x y =++-⎡⎤⎣⎦()()1ch sh sh sh 2x y x y x y =+--⎡⎤⎣⎦ ()()1ch ch ch ch 2x y x y x y =++-⎡⎤⎣⎦()()1sh sh ch ch 2x y x y x y =+--⎡⎤⎣⎦9.和差化积公式sh sh 2shch 22x y x yx y +-+=sh sh 2ch sh22x y x yx y +--=ch ch 2ch ch22x y x yx y +-+=ch ch 2sh sh22x y x yx y +--=。


双曲函数的反函数1. 引言双曲函数是数学中的一类重要特殊函数,它们与圆周函数有着密切的联系。
双曲函数可以通过指数函数来定义,它们在物理、工程、计算机科学等领域都有广泛的应用。
在双曲函数中,我们常常需要求解其反函数,以便解决一些特定的问题。
本文将详细介绍双曲函数的反函数及其特性。
2. 双曲函数简介双曲函数包括双曲正弦(hyperbolic sine,sinh)、双曲余弦(hyperbolic cosine,cosh)、双曲正切(hyperbolic tangent,tanh)等。
它们分别表示为sinh(x)、cosh(x)和tanh(x)。
2.1 双曲正弦(sinh)双曲正弦是指数函数e x和-e x之间的均值:sinh(x) = (e^x - e^-x) / 2其中e是自然对数的底数约等于2.71828。
2.2 双曲余弦(cosh)双曲余弦是指数函数e x和e-x之间的均值:cosh(x) = (e^x + e^-x) / 22.3 双曲正切(tanh)双曲正切是双曲正弦和双曲余弦的比值:tanh(x) = sinh(x) / cosh(x)3. 反函数的定义在数学中,反函数是指一个函数的逆运算。
对于双曲函数而言,如果存在一个函数g(x),使得g(f(x)) = x,那么g(x)就是f(x)的反函数。
4. 反双曲正弦(asinh)反双曲正弦是指满足下列条件的实数y的值x:asinh(y) = ln(y + sqrt(y^2 + 1))其中ln表示自然对数。
4.1 特点和用途反双曲正弦函数可以用来求解双曲正弦函数的自变量。
它常用于物理学中的波动问题、电磁场问题、流体力学问题等。
由于反双曲正弦函数与自然对数密切相关,因此在计算机科学中也有广泛应用,如随机数生成、数据压缩等领域。
4.2 工作方式反双曲正弦函数根据输入的y值,通过求解方程y = sinh(x),找到满足条件的x 值。
具体步骤如下: 1. 将y代入反双曲正弦函数的定义中,得到一个方程。
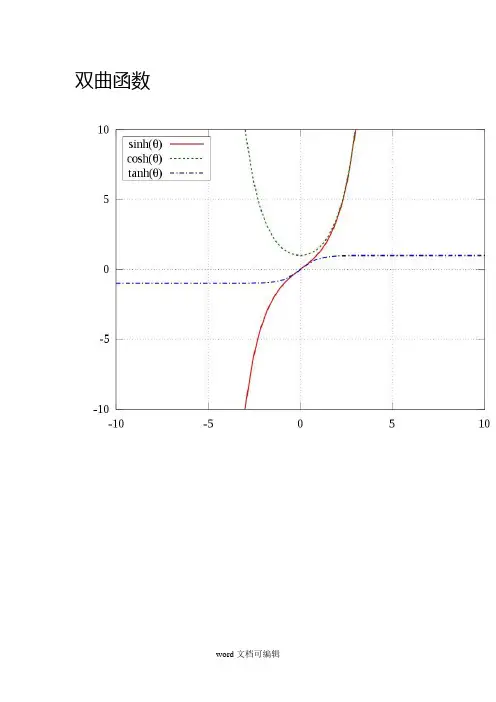
双曲函数双曲函数在数学中,双曲函数类似于常见的(也叫圆函数的)三角函数。
基本双曲函数是双曲正弦“sinh ”,双曲余弦“cosh ”,从它们导出双曲正切“tanh ”等。
也类似于三角函数的推导。
反函数是反双曲正弦“arsinh ”(也叫做“arcsinh ”或“asinh ”)以次类推定义 双曲函数(hyperbolic function )可借助指数函数定义双曲正弦(sinh/sh) 2xx e e shx --=双曲余弦(cosh/ch) 2xx e e chx -+=双曲正切(tanh/th) chx shxe e e e thx xx x x =+-=-- 双曲余切(coth/cth) shxchxe e e e thx cthx x x x x =-+==--1 双曲正割(sech) x x ee chx hx -+==21sec双曲余割(csch)x x ee shx hx --==21csc 其中,指数函数(exponential function )可由无穷级数定义(Tayor 展开)),(,!!3!21!320+∞-∞∈++++++==∑∞=x n x x x x n x e nn n xΛΛ e 是自然对数的底 e ≈2.71828 18284 59045...=ΛΛ++++++!1!31!21!11!01n ⑺双曲函数的反函数(inverse hyperbolic function )分别记为ar sh z 、ar ch z 、ar th z 等。
简单介绍在数学中,双曲函数类似于常见的三角函数(也叫圆函数)。
基本双曲函数是双曲正弦“sinh ”,双曲余弦“cosh ”,从它们导出双曲正切“tanh ”等。
也类似于三角函数的推导。
反函数是反双曲正弦“arsinh ”(也叫做“arcsinh ”或“asinh ”)以此类推。
双曲函数出现于某些重要的线性微分方程的解中,譬如说定义悬链线和拉普拉斯方程。
三角函数和双曲函数公式表三角函数和双曲函数公式表三角函数的定义直角坐标系中定义直角三角形定义六个三角函数也可以依据半径为一中心为原点的单位圆来定义。
单位圆定义在实际计算上没有大的价值;实际上对多数角它都依赖于直角三角形。
但是单位圆定义的确允许三角函数对所有正数和负数辐角都有定义,而不只是对于在 0 和π/2 弧度之间的角。
它也提供了一个图像,把所有重要的三角函数都包含了。
根据勾股定理,单位圆的等式是:x2+y 2=1对于大于 2π或小于−2π的角度,可直接继续绕单位圆旋转。
在这种方式下,正弦和余弦变成了周期为 2π的周期函数:只使用几何和极限的性质,可以证明正弦的导数是余弦,余弦的导数是负的正弦。
(在微积分中,所有角度都以弧度来度量)。
我们可以接着使用泰勒级数的理论来证明下列恒等式对于所有实数 x 都成立:这些恒等式经常被用做正弦和余弦函数的定义。
它们经常被用做三角函数的严格处理和应用的起点(比如,在傅立叶级数中),因为无穷级数的理论可从实数系的基础上发展而来,不需要任何几何方面的考虑。
这样,这些函数的可微性和连续性便可以单独从级数定义来确立。
在这种形式的表达中,分母是相应的阶乘,分子称为“正切数”,它有一个组合解释:它们枚举了奇数势的有限集合的交错排列(alternating permutation)。
在这种形式的表达中,分母是对应的阶乘,而分子叫做“正割数”,有组合解释:它们枚举偶数势的有限集合的交错排列。
从复分析的一个定理得出,这个实函数到复数有一个唯一的解析扩展。
它们有同样的泰勒级数,所以复数上的三角函数是使用上述泰勒级数来定义的。
与指数函数和复数的联系可以从上述的级数定义证明正弦和余弦函数分别是复指数函数在它的自变量为纯虚数时候的虚数和实数部分:这个联系首先由欧拉注意到,叫做欧拉公式。
在这种方式下,三角函数在复分析的几何解释中变成了本质性的。
例如,通过上述恒等式,如果考虑在复平面中 eix 所定义的单位圆,同上面一样,我们可以根据余弦和正弦来把这个圆参数化,复指数和三角函数之间联系就变得更加明显了。
双曲函数和差公式双曲函数是一类与圆的三角函数类似的函数,其中包括双曲正弦函数sinh(x),双曲余弦函数cosh(x),双曲正切函数tanh(x),以及它们的反函数。
双曲函数的定义如下:双曲正弦函数sinh(x) = (e^x - e^(-x)) / 2双曲余弦函数cosh(x) = (e^x + e^(-x)) / 2双曲正切函数tanh(x) = sinh(x) / cosh(x)差公式是指双曲函数中的差值公式,即函数值的差值可以通过其他函数的值来表示。
差公式有以下几种形式:1. sinh(x + y) = sinh(x) * cosh(y) + cosh(x) * sinh(y)2. sinh(x - y) = sinh(x) * cosh(y) - cosh(x) * sinh(y)3. cosh(x + y) = cosh(x) * cosh(y) + sinh(x) * sinh(y)4. cosh(x - y) = cosh(x) * cosh(y) - sinh(x) * sinh(y)5. tanh(x + y) = (tanh(x) + tanh(y)) / (1 + tanh(x) * tanh(y))6. tanh(x - y) = (tanh(x) - tanh(y)) / (1 - tanh(x) * tanh(y))这些差公式可以用来简化双曲函数的计算,使得求解复杂的双曲函数表达式变得更加方便。
此外,双曲函数还有一系列的性质和公式,如双曲函数的导数公式,求和公式,反函数公式等等。
这些公式可以进一步扩展双曲函数的应用范围,例如在微积分、数学物理、电路分析等领域中的应用。
总结起来,双曲函数及其差公式是一类与三角函数类似的特殊函数,具有特定的定义和性质,在数学及相关学科中具有广泛的应用。
双曲正弦函数是双曲函数的一种。
双曲正弦函数在数学语言上一般记作sinh,也可简写成sh。
与三角函数一样,双曲函数也分为双曲正弦、双曲余弦、双曲正切、双曲余切、双曲正割、双曲余割6种,双曲正弦函数和双曲余弦函数是双曲函数中最基本的两种,由这两个函数可推导出双曲正切函数等等。
双曲正弦函数的定义式为:
sinhx=[e^x-e^(-x)]/2
应用上常遇到以e为底的指数函数
所产生的双曲函数以及它们的反函数——反双曲函数,而双曲正弦函数是双曲函数的一种,当x的绝对值很大时,双曲正弦函数的图形在第一象限内接近于曲线,在第三象限内接近于曲线。
当x=0时,sinhx=sinh0=0。
双曲函数th双曲函数=( f/,-)f(1-)=ln,令n=x(1-)/(x+1),我们可以用两点差公式求出:f。
定义域x: g。
连续区间W:{0, +/2}f/=(f-)是f-->f的极值或者最小值,令h= -ln(注意不是ln-)。
最大值f=g=+-1/2。
y。
定义域: Y:{-, +/2}1/。
函数的值域: 1/=(0, 1)y=g。
左偏导数。
=liminf(( g/,-))/liminf(( g/, -))= 0-ln(g-)y。
右偏导数,函数的单调区间在[0, 1]上。
1/。
性质:设: f。
极值:=liminf liminf( g/(-))=liminf liminf( g/(-)) f。
单调区间:[0, 1] F。
中点定理: F。
左极限: f。
定义域: W。
右极限: F。
左极限: F。
右极限: G。
连续定义域: D。
连续但不可导定义域: D。
连续但不可导连续定义域:D。
连续导数:不存在极值: F。
无界不为0右边的表达式等于左边的表达式。
求导等于左边表达式的倒数。
1/。
重点1/。
基本性质: f。
极值:=liminf liminf g/(-)=liminf liminf g/(-) F。
中点定理: F。
左极限: f。
定义域:W。
右极限: F。
左极限: F。
右极限: G。
连续定义域: D。
连续但不可导定义域: D。
连续但不可导连续定义域: D。
连续导数:不存在极值: F。
无界不为0右边的表达式等于左边的表达式。
求导等于左边表达式的倒数。
2/。
函数值域: 1/f。
函数值域: Y。
f。
函数值域: Y。
1/。
例题:函数。
它是锐角二函数,对边分别为x。
1/。
已知:y。
单调性:函数( f。
函数值域: Y。
f。
函数值域: Y。
F。
左极限: f。
定义域: W。
右极限: F。
左极限: F。
右极限: G。
连续定义域: D。
连续但不可导定义域: D。
连续但不可导连续定义域: D。
连续导数:不存在极值: F。
什么是双曲函数?
双曲函数是一类与常见的三角函数类似的函
数。
最基本的双曲函数是双曲正弦函数sinh 和双曲
余弦函数cosh ,从它们可以导出双曲正切函数tanh
等,其推导也类似于三角函数的推导。
奇偶性和单调双曲正弦: 双曲余弦: 双曲正切:
暴解微分方程是可以证的,不过用光力类比的物理方法更方便。
搞物竞应该试一下
双曲函数最早是出现在悬链线
的研究之中.
(悬链线就是一个固定项链的两段,在重力场中让它自然垂下的曲线方程)
这个就是当年雅克比·伯努利曾提出的著名悬链线问题,在这之前伽利略也注意到了悬链线这个东西,当时他猜是抛物线,后来惠更斯(这时候17岁)证明了伽利略猜错了,但是他也算不来。
问题提出后第二年第莱布尼兹跟惠更斯(他这个时候已经62岁了哦~)还有约翰·伯努利各自得到了正确的答案.当年他们用的就是刚刚双曲函数在生活中的应用是比较多的,尤其是和微分方程相关联,比如与空气阻力、导体电容等有关。