双曲函数及其几何意义

双曲线b的几何意义
双曲线是一种具有曲线的几何图形，它有两个曲线，被称为双曲线b。

它的几何意义是，它是一种反比例函数，即当一
个变量增加时，另一个变量减少，反之亦然。

这个关系可以用曲线来表示。

双曲线b可以用一个变量x表示，另一个变量y也可以表示，这两个变量之间的关系可以用一个关系式来表示：y=1/x。

因此，双曲线b的几何意义是，当x增加时，y减少，反之亦然。

双曲线b的几何意义被广泛应用于数学、物理和化学等科学领域。

例如，在物理学中，双曲线b可以用来描述一个物体的力学运动；在化学中，它可以用来描述反应的速率；在数学中，它可以用来描述曲面的几何形状。

双曲线b还被广泛应用于商业领域，如财务分析、市场研究和经济学等。

例如，双曲线b可以用来描述消费者的需求和价格之间的关系，以及企业的收入和利润之间的关系。

双曲线
b还可以用来描述投资者的风险和回报之间的关系，以及市场
的供求关系等。

总之，双曲线b的几何意义是，它是一种反比例函数，表示两个变量之间的关系，它被广泛应用于数学、物理、化学和商业等不同领域。

反比例函数中K的几何意义
在反比例函数中，K表示比例系数或常数，也被称为反比例常数。

它
是用来确定两个变量之间反比关系的重要参数。

反比例函数的一般形式为：y=K/x，其中K表示比例系数。

K的几何意义可以通过分析反比例函数的图像得出。

反比例函数的图
像是一个双曲线，特点是曲线趋向于两个坐标轴。

下面将详细讨论K的几
何意义。

1.K的符号对于曲线的位置以及开口方向具有重要影响。

如果K为正数，那么曲线将位于第一和第三象限，并且开口方向为右上和左下。

如果
K为负数，那么曲线将位于第二和第四象限，并且开口方向为左上和右下。

2.K的绝对值越大，曲线就越“陡峭”。

当K增大时，曲线将更加接
近于坐标轴，并且在原点附近的斜率会越来越大。

反之，当K变小时，曲
线将更加平缓，斜率将减小。

3.K决定了特定坐标点的函数值。

例如，在函数y=K/x中，当x为K 时，y的值将为1、这是因为x与y成反比关系，而K是这种关系的常数。

4.K还决定了曲线相对于坐标轴的位置。

具体而言，当K增大时，曲
线将向坐标轴移动，而当K减小时，曲线将远离坐标轴。

总之，K代表了反比例函数中的比例系数或常数，它对于函数的位置、开口方向、陡峭程度以及特定坐标点的函数值都具有重要影响。

通过对K
的分析，我们可以更好地理解和解释反比例函数的几何特征。

函数几何知识点总结一、函数的几何意义函数的几何意义是指函数在几何中的表现和应用。

在几何中，函数可以被用来描述和分析各种图形和曲线的形态、性质和特点。

函数的几何意义通常是通过函数的图像来展现的。

1.1 函数的图像函数的图像是函数在平面直角坐标系中的表现形式，通过绘制函数的图像，我们可以直观地看到函数的性质和特点。

对于一元函数f(x)，其图像是由一组点(x, f(x))构成的集合，这些点表示了函数在定义域上的取值情况。

函数的图像可以帮助我们直观地理解函数的变化规律和特点，例如函数的增减性、奇偶性、周期性、极限性等。

通过函数的图像，我们可以了解函数的几何特性，以及函数与其他图形之间的关系。

1.2 函数的几何性质在几何中，函数的几何性质是指函数在平面几何中的几何特点和规律。

通过函数的图像和几何分析，我们可以得到函数的一些重要几何性质，如函数的极值、拐点、渐近线、对称轴等。

函数的极值是指函数在定义域内取得的最大值和最小值，函数的极值可以通过函数的导数和二阶导数进行求解。

函数的拐点是指函数图像上的点，其切线在该点处有一个拐点，即函数的导数的变化率发生突变的点。

函数的渐近线是指函数图像在无限远处的一个趋势线，通过渐近线可以描述函数的趋势和变化规律。

函数的对称轴是指函数图像上存在的一条对称轴线，函数关于对称轴线呈现对称性。

1.3 几何图形的方程函数可以用来描述和分析各种几何图形的形态和性质，例如直线、圆、椭圆、双曲线、抛物线等。

在几何中，通过函数的方程我们可以得到各种几何图形的数学描述，例如直线的方程可以用一元一次函数来表示，圆的方程可以用二元二次函数来表示。

通过函数的方程，我们可以分析几何图形的各种性质和特点，例如直线的斜率和截距、圆的半径和圆心、椭圆的焦点和长轴、双曲线的渐近线和焦点等。

函数的方程在几何中有着广泛的应用，可以帮助我们更好地理解几何图形的形态和性质。

二、函数的性质函数的性质是函数在数学中的一些重要特点和规律，这些性质包括增减性、奇偶性、周期性、单调性、最值和极值等。

高考双曲线知识点高考双曲线知识点在我们的学习时代，大家都背过不少知识点，肯定对知识点非常熟悉吧！知识点是传递信息的基本单位，知识点对提高学习导航具有重要的作用。

相信很多人都在为知识点发愁，下面是店铺精心整理的高考双曲线知识点，欢迎阅读，希望大家能够喜欢。

高考双曲线知识点篇1高考双曲线知识点1.双曲线定义的文字表述双曲线，是指一动点移动于一个平面上，与平面上两个定点的距离的差的绝对值始终为一定值时所成的轨迹叫做双曲线。

2.双曲线定义的分析1)点:两个定点 ,一个动点2)距离:三个3)量:两个(常数)4)关系式:两个;一个等式 ,一个不等式3.判断一个动点轨迹是否是双曲线的标准1)看动点到两个定点的距离的差的绝对值是否为常数2)看这个常数是否小于两个定点之间的距离高考数学三角函数知识点一、三角函数三角函数的定义域是研究其他一切性质的前提，求三角函数的定义域实际上就是解最简单的三角不等式，通常可用三角函数的图像或三角函数线来求解，注意数形结合思想的应用,如何运用三角函数的图像解决问题能够帮助对数形结合思想的掌握。

二、三角函数诱导公式1.公式一：设α为任意角，终边相同的角的同一三角函数的值相等运用同角三角函数的基本关系式求值2.公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin(π+α)=—sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα公式三：任意角α与-α的三角函数值之间的关系：sin(-α)=-sinα高考数学几何定理1 过两点有且只有一条直线2 两点之间线段最短3 同角或等角的补角相等4 同角或等角的余角相等5 过一点有且只有一条直线和已知直线垂直6 直线外一点与直线上各点连接的所有线段中，垂线段最短7 平行公理经过直线外一点，有且只有一条直线与这条直线平行8 如果两条直线都和第三条直线平行，这两条直线也互相平行9 同位角相等，两直线平行10 内错角相等，两直线平行11 同旁内角互补，两直线平行12 两直线平行，同位角相等13 两直线平行，内错角相等14 两直线平行，同旁内角互补15 定理三角形两边的和大于第三边16 推论三角形两边的差小于第三边17 三角形内角和定理三角形三个内角的和等于180°18 推论1 直角三角形的两个锐角互余19 推论2 三角形的一个外角等于和它不相邻的两个内角的和20 推论3 三角形的一个外角大于任何一个和它不相邻的内角猜你感兴趣：1.2018高考数学知识点归纳总结2.高考数学知识点总结3.2018数学高考知识点4.高考导数大题解题技巧5.8年级下册数学知识点6.2018高考全国卷I理科数学试卷评析高考双曲线知识点篇2一、用好双曲线的对称性例1若函数y=kx(k>0)与函数y=的图象相交于A、C两点，AB⊥x 轴于B。

反比例函数高频考点重难点总结一、反比例函数的概念：一般地，形如 y = k/x ( k是常数, k ≠ 0 ) 的函数叫做反比例函数。

二、反比例函数的图象和性质：1、形状：图象是双曲线。

2、位置：（1）当k>0时,双曲线分别位于第一、三象限内；（2）当k<0时,>3、增减性：（1）当k>0时,在每个象限内，y随x的增大而减小；（2）当k<>在每个象限内，y随x的增大而增大。

4、变化趋势：双曲线无限接近于x、y轴，但永远不会与坐标轴相交。

5、对称性：（1）对于双曲线本身来说，它的两个分支关于直角坐标系原点中心对称；（2）对于k取互为相反数的两个反比例函数（如：y = 6/x 和y = -6/x）来说，它们是关于x轴，y轴对称。

三、反比例函数中比例系数k的几何意义：1、反比例函数与矩形面积：若P(x，y)为反比例函数y=k/x(k≠0)图像上的任意一点如图1所示，过P作PM⊥x轴于M，作PN⊥y轴于N，求矩形PMON的面积.分析：S矩形PMON=PM·PN=│y│·│x│=│xy│∵y=k/x,∴ xy=k,∴S =│k│.2、反比例函数与三角形面积：若Q(x，y)为反比例函数y=k/x(k≠0)图像上的任意一点如图2所示，过Q作QA⊥x轴于A(或作QB⊥y轴于B)，连结QO，则所得三角形的面积为：S△QOA=│k│/2（或S△QOB=│k│/2）.说明：以上结论与点在反比例函数图像上的位置无关.四、反比例函数图像与一次函数图像的交点（难点）求两个函数图像的交点，往往把两个函数的表达式联立组成方程组，方程组的解就是交点的坐标。

（1）正比例函数y=k₁x(k₁≠0)与反比例函数y=k₂/x(k₂≠0),当k₁与k₂同号时，正比例函数图像与反比例函数图像有两个交点，即对应方程组的解，且两个交点关于原点对称；当k₁与k₂异号时，两个函数图像没有交点。

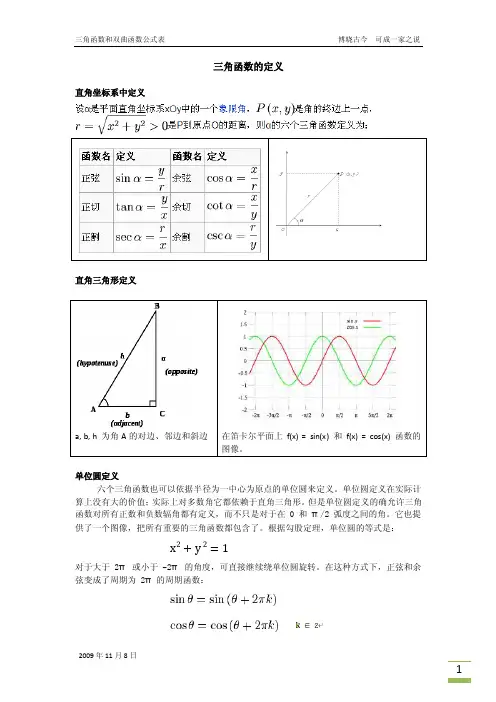
三角函数的定义直角坐标系中定义直角三角形定义a, b, h 为角A的对边、邻边和斜边在笛卡尔平面上f(x) = sin(x) 和f(x) = cos(x) 函数的图像。

单位圆定义六个三角函数也可以依据半径为一中心为原点的单位圆来定义。

单位圆定义在实际计算上没有大的价值；实际上对多数角它都依赖于直角三角形。

但是单位圆定义的确允许三角函数对所有正数和负数辐角都有定义，而不只是对于在 0 和π/2 弧度之间的角。

它也提供了一个图像，把所有重要的三角函数都包含了。

根据勾股定理，单位圆的等式是：x2+y2=1对于大于 2π或小于−2π的角度，可直接继续绕单位圆旋转。

在这种方式下，正弦和余弦变成了周期为 2π的周期函数：级数定义只使用几何和极限的性质，可以证明正弦的导数是余弦，余弦的导数是负的正弦。

（在微积分中，所有角度都以弧度来度量）。

我们可以接着使用泰勒级数的理论来证明下列恒等式对于所有实数x都成立：这些恒等式经常被用做正弦和余弦函数的定义。

它们经常被用做三角函数的严格处理和应用的起点（比如，在傅立叶级数中），因为无穷级数的理论可从实数系的基础上发展而来，不需要任何几何方面的考虑。

这样，这些函数的可微性和连续性便可以单独从级数定义来确立。

在这种形式的表达中，分母是相应的阶乘，分子称为“正切数”，它有一个组合解释：它们枚举了奇数势的有限集合的交错排列（alternating permutation）。

在这种形式的表达中，分母是对应的阶乘，而分子叫做“正割数”，有组合解释：它们枚举偶数势的有限集合的交错排列。

从复分析的一个定理得出，这个实函数到复数有一个唯一的解析扩展。

它们有同样的泰勒级数，所以复数上的三角函数是使用上述泰勒级数来定义的。

与指数函数和复数的联系可以从上述的级数定义证明正弦和余弦函数分别是复指数函数在它的自变量为纯虚数时候的虚数和实数部分：这个联系首先由欧拉注意到，叫做欧拉公式。

在这种方式下，三角函数在复分析的几何解释中变成了本质性的。