下载文档原格式
双曲函数在物理学中的应用摘 要：数学上有两个十分重要的函数，一个是自然指数函数，还有一个就是双曲函数，因为这两个重要的函数都离开不了e 。
所以我们可以知道双曲函数是一类用指数函数定义的初等函数。
双曲函数在生活中有着广泛的应用，它就存在我么的身边。
双曲函数就是根据悬链线推到出的函数。
在上个世纪六十年代以来西方的桥梁建筑中就出现了悬链线形状的拱桥，坚固程度可谓是坚不可摧。
足以说明双曲函数的重要性。
双曲函数在数学中也有着很重要的地位，从悬链线到繁衍几何和双曲几何，都应用到了双曲函数，同是在数学某些相应的方程中也出现了和双曲函数有关的解，比如说拉普拉斯方程就是用其来定义的。
可见其在数学中的重要性。
本文给出了双曲函数的定义，并例举一些典型的例子说明其在物理学中也有着十分广泛应用，使读者对双曲函数予以其足够的重视。
关键词：双曲函数 物理学 悬链线 阻尼落体 电容引 言：双曲函数是雅比•伯努利及其他数学家根据两端固定于两个固定点的均匀绳索，在只受自身重力的作用下形成的曲线推导出来的。
由于指数函数具有自己独特的性质，很多函数都用其表示，双曲函数也是这样一类用指数函数定义的函数。
十七世纪雅比•伯努利提出了两端固定于两个固定点的均匀绳索，在只受自身重力的情况下形成的曲线是什么曲线的问题。
一开始他本人和伽利略都误以为是一条抛物线，但随后雅比•伯努利和一些其他的数学家用微分方程推导出了这条曲线的方程，进而发现这是一个新的函数“双曲函数”。
这条线就是我们所谓的悬链线。
双曲函数(hyperbolic function)的定义 双曲正弦2)(e e zz shz --=双曲余弦2)(chz e ze z-+=双曲正切)()(chz shz thz e e e e zzzz--+-==双区余切)()(e e e e zzzzshz chz cthz ---+==双曲正割chz hz 1sec =双曲余割shz hz 1csc =其中，其中，指数函数由无穷级数定义...!...!4!3!2!11432z+++++++=n z z z z z en双曲函数的反函数反双曲正弦：()2ln1arshz z z =±+反双曲余弦：()2ln1archz z z =±-反双曲正切：11l n 21za r t h zz+=-双曲函数的性质：221c h z s h z -=c o t h1t h z z ⋅=221sech th z z -=22coth 1csch z z-=()s hxys h x c h y c h x s h y±=± ()c h x y c h x s h y s h x c h y±=±()1t h x t h y t hxyt h x t h y±±=±22s h x s h x c h x=222222121ch x ch x sh x ch x sh x =+=-=+2221t h x t h xt h x=+双曲函数与三角函数的关系sin shz i iz=-c o s c h z i z=tan thz i iz=-coth cot z i iz =sech sec z iz =c s c h c s c z i c i z=下面让我们来用几个相应的例子来说明双曲函数在物理中也是有着广泛的应用。
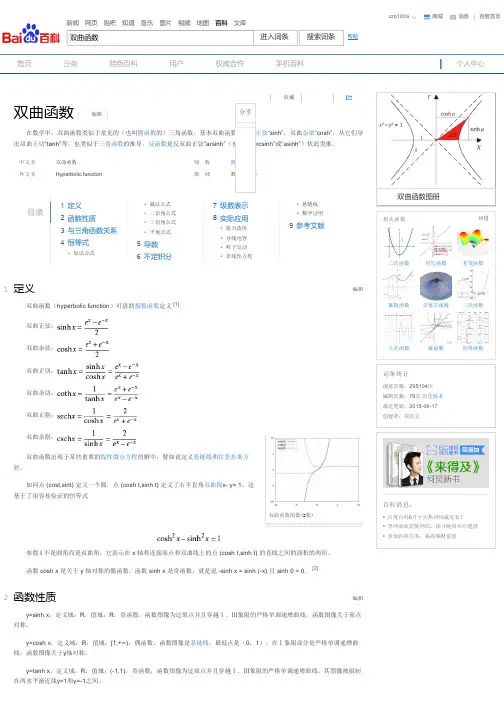
反双曲函数泰勒展开反双曲函数，也称作反双曲正弦函数、反双曲余弦函数和反双曲正切函数，是与双曲函数相对应的函数。
反双曲函数在数学和物理学中具有广泛的应用，特别是在微积分和微分方程的解析中，起到了重要的作用。
在本文中，我们将探讨反双曲函数的泰勒展开，了解其背后的数学原理，并且深入探讨其在实际问题中的应用。
1. 什么是反双曲函数？反双曲函数是与双曲函数相反的映射关系。
在数学中，双曲函数是指双曲正弦函数、双曲余弦函数和双曲正切函数。
反双曲函数则是将双曲函数的值映射回原来的自变量上，从而得到一个方程的解。
常见的反双曲函数有反双曲正弦函数asin(x)，反双曲余弦函数acos(x)和反双曲正切函数atan(x)。
2. 反双曲函数的泰勒展开泰勒展开是一种将给定函数表示为无穷级数的方法，从而使函数在某一点附近以多项式的形式近似。
对于反双曲函数而言，其泰勒展开可以用来近似计算非常小或非常大的值。
以反双曲正弦函数asin(x)的泰勒展开为例，其泰勒展开式为：asin(x) = x + (1/2)x^3/3! + (1*3)/(2*4)x^5/5! +(1*3*5)/(2*4*6)x^7/7! + ...在这个级数中，每一项的系数都与自变量x的次数和阶乘有关。
这意味着将更多的项包括在级数中，可以更准确地近似反双曲正弦函数。
同样地，反双曲余弦函数acos(x)和反双曲正切函数atan(x)也可以用类似的方法进行泰勒展开。
3. 反双曲函数的应用反双曲函数在实际问题中有着广泛的应用。
下面我们将介绍两个应用反双曲函数的例子。
例子一：天体力学在天体力学中，反双曲函数被用来计算天体的轨道。
通过使用反双曲函数，可以解决行星、卫星和彗星等天体运动的问题。
这些问题往往需要求解椭圆轨道或抛物线轨道的方程，反双曲函数提供了一种有效的数学工具来解决这些方程。
例子二：电路分析在电路分析中，反双曲函数也经常被使用。
在变频电路中，反双曲正切函数可以用来表示复杂的电压和电流波形。
Hyperbolic functions(双曲函数）and their geometric meaningIn mathematics, hyperbolic functions are analogs of the ordinary trigonometric, or circular, functions. The basic hyperbolic functions are the hyperbolic sine "sinh" (/ˈsɪnt ʃ/ or /ˈʃaɪn/), and the hyperbolic cosine "cosh" (/ˈkɒʃ/), from which are derived the hyperbolic tangent "tanh" (/ˈtæntʃ/ or /ˈθæn/), hyperbolic cosecant "csch" or "cosech" (/ˈkoʊʃɛk/ or /ˈkoʊsɛtʃ/), hyperbolic secant "sech" (/ˈʃɛk/ or /ˈsɛtʃ/), and hyperbolic cotangent "coth" (/ˈkoʊθ/ or /ˈkɒθ/),[1] corresponding to the derived trigonometric functions. The inverse hyperbolic functions are the area hyperbolic sine "arsinh" (also called "asinh" or sometimes "arcsinh")[2] and so on.Just as the points (cos t, sin t) form a circle with a unit radius, the points (cosh t, sinh t) form the right half of the equilateral hyperbola. The hyperbolic functions take a real argument called a hyperbolic angle. The size of a hyperbolic angle is the area of its hyperbolic sector. The hyperbolic functions may be defined in terms of the legs of a right triangle covering this sector.Hyperbolic functions occur in the solutions of some important linear differential equations, for example the equation defining a catenary, of some cubic equations, and of Laplace's equation in Cartesian coordinates. The latter is important in many areas of physics, including electromagnetic theory, heat transfer, fluid dynamics, and special relativity.In complex analysis, the hyperbolic functions arise as the imaginary parts of sine and cosine. When considered defined by a complex variable, the hyperbolic functions are rational functions of exponentials, and are hence meromorphic.Hyperbolic functions were introduced in the 1760s independently by Vincenzo Riccati and Johann Heinrich Lambert.[3] Riccati used Sc. and Cc. ([co]sinus circulare) to refer to circular functions and Sh. and Ch. ([co]sinus hyperbolico) to refer to hyperbolic functions. Lambert adopted the names but altered the abbreviations to what they are today.[4] The abbreviations sh and ch are still used in some other languages, like European French and Russian.A ray through the origin intercepts the unit hyperbola in the point , where is twice the area between the ray, the hyperbola, and the -axis. For points on the hyperbola below the -axis, the area is considered negative (see animated version with comparison with the trigonometric (circular) functions).。
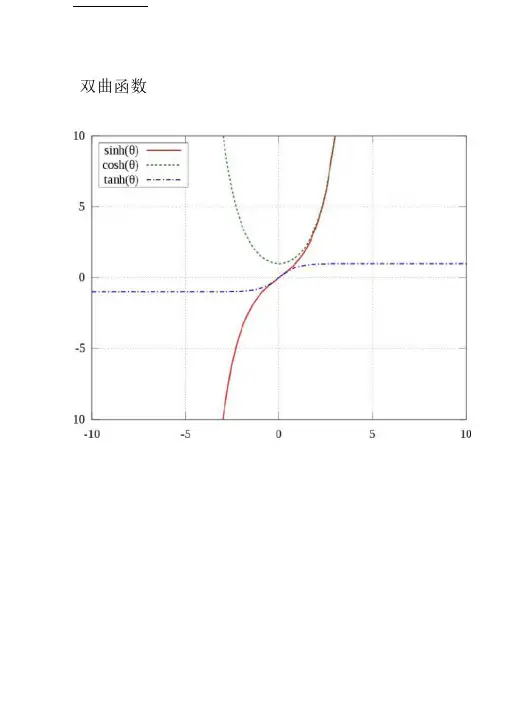
双曲函数双曲函数在数学中，双曲函数类似于常见的（也叫圆函数的）三角函数。
基本双曲函数是双曲 正弦sinh ”双曲余弦“osh ”从它们导出双曲 正切fanh "等。
也类似于三角函数的推导。
反函数 是反双曲正弦 arsinh "（也叫做arcsinh"或asinh ”以次类推双曲函数（hyperbolic function ）可借助 指数函数 定义510定义 双曲正弦（sinh/sh ）shx双曲余弦（cosh/ch ）双曲正切（tanh/th ）双曲余切（coth/cth ）双曲正割（sech ）x xe echx -----------2thxsechxchxx e e xchx1xe e <thxx e e12chx shxshx xxxexexxe e简单介绍在数学中，双曲函数类似于常见的三角函数（也叫圆函数）。
基本双曲函数是双曲正弦sinh ”，双曲余弦cosh”，从它们导出双曲正切f3nh "等。
也类似于三角函数的推导。
反函数是反双曲正弦arsinh ”（也叫做arcsinh "或asinh”）以此类推。
双曲函数出现于某些重要的线性微分方程的解中，譬如说定义悬链线和拉普拉斯方程。
双曲函数接受实数值作为叫做双曲角的自变量。
在复分析中，它们简单的是指数函数的有理函数，并因此是完整的。
射线出原点交双曲线x2 - y2 = 1于点（ch a,sh a），这里的a被称为双曲角，是这条射线、它关于x轴的镜像和双曲线之间的面积。
如图点（cost,si nt）定义一个圆，点（ch t,sh t）定义了右半直角双曲线x2y 1这基于了很容易验证的恒等式ch2x sh2x 1 和性质t > 0对于所有的t。
参数t不是圆角而是双曲角，匕表示在x轴和连接原点和双曲线上的点(ch t,sh t)的直线之间的面积的两倍。
函数cosh x是关于y轴对称的偶函数。
双曲函数介绍在数学中，双曲函数类似于常见的三角函数（也叫圆函数）。
基本双曲函数是双曲正弦“sinh”，双曲余弦“co snh”，从它们导出双曲正切“tanh”等。
也类似于三角函数的推导。
反函数是反双曲正弦“ar c sinh”（也叫做“arcsinh”或“asinh”）以此类推。
双曲函数出现于某些重要的线性微分方程的解中，譬如说定义悬链线和拉普拉斯方程。
双曲函数接受实数值作为叫做双曲角的自变量。
在复分析中，它们简单的是指数函数的有理函数，并因此是完整的。
射线出原点交双曲线 x^2 - y^2 = 1 于点 (cosinh a,sinh a），这里的a被称为双曲角，是这条射线、它关于x轴的镜像和双曲线之间的面积。
定义双曲函数（Hyperbolic Function）包括下列六种函数：sinh / 双曲正弦：sinh(x) = [e^x - e^(-x)] / 2cosh / 双曲余弦：cosh(x) = [e^x + e^(-x)] / 2tanh / 双曲正切：tanh(x) = sinh(x) / cosh(x)=[e^x - e^(-x)] / [e^x + e^(-x)]coth / 双曲余切：coth(x) = cosh(x) / sinh(x) = [e^x + e^(-x)] / [e^(x) - e^(-x)]sech / 双曲正割：sech(x) = 1 / cosh(x) = 2 / [e^x + e^(-x)]csch / 双曲余割：csch(x) = 1 / sinh(x) = 2 / [e^x - e^(-x)]其中，e是自然对数的底e≈2.71828 18284 59045...= 1/0! + 1/1! + 1/2! + 1/3! + 1/4! + 1/5! + 1/n! +...e^x 表示 e的x次幂,展开成无穷幂级数是：e^x=x^0/0! + X^1/1! + X^2/2! + X^3/3! + X^4/4! + X^5/5!...+ x^n/n! +...如同点 (cost,sint) 定义一个圆，点 (cosh t,sinh t) 定义了右半直角双曲线x^2 y^2 = 1。
探究双曲函数PB07210142,梁海波双曲函数是我们在大学时期微积分课程中新接触的东东，但仿佛仅在《高等数学导论》第一章有所提及，貌似与后来知识没有关系。
本人在做题时发现，双曲函数与后来的微积分，特别是积分求解有许多联系。
首先，我们先认识下双曲函数。
双曲正弦:2xx e e shx --=双曲余弦: 2xx e e chx -+= 双曲正切: x x xx ee e e thx --+-= 双曲函数与三角函数有很多相似的性质,在求解积分的过程中,三角函数与双曲函数地位相当,下面对其相似之处进行比较,由于三角函数性质在以前接触较多,这里不在赘述.chxshx thx = chxshy shxchy y x sh ±=±)(shxshy chxchy y x ch ±=±)(122=-x sh x chx ch x sh x ch 222=+shx x sh -=-)(chx x ch =-)(shxchx x sh 22=下面说反双曲函数。
以下记法与书上不同，这样写便于与反三角函数想对比。
)1ln(2-+±=x x arcchx)1ln(2++=x x arcshx)11ln(21xx arcthx -+= 求解积分的问题中，有很多式子含有12-x ，12+x 以及它的倒数与根式形。
书后的简明积分表也给出了相关的公式，但这些公式复杂难记，没能把握住其与双曲函数的内在关系。
我们在解这类问题时往往会采用换元法，令x=sint 或x=sht 等。
其实这样设的目的就是利用了反三角函数，反双曲函数的微分，下面对这些公式作一定的改写。
（１）dx x⎰+211＝c x +arctan c arcthx dx x +=-⎰211（２）||112arcchx dx x =-⎰c x dx x +=-⎰arcsin 112 c x dx x +=--⎰arccos 112 c arcshx dx x +=+⎰112 （３）2212arcsin 211x x x dx x -+=-⎰ 2212211x x arcshx dx x ++=+⎰ 12||21122-+-=-⎰x x arcchx dx x从形式上简化，实质是从思想上的简化，这样去理解公式不仅便于记忆，更加深了我们对双曲函数的理解。
数学双曲线知识点总结一、双曲线的定义1. 定义：双曲线是平面上一个点到两个给定点的距离之差等于一个常数的动点轨迹。
这两个给定点称为焦点，常数称为离心率。
双曲线的离心率小于1。
双曲线有两个分支，每个分支有一组渐近线。
2. 方程：双曲线的标准方程为x^2/a^2 - y^2/b^2 = 1。
其中，a和b分别为双曲线在x轴和y轴上的焦点坐标。
3. 参数方程：双曲线的参数方程为x = a·secθ, y = b·tanθ。
其中，a和b分别为双曲线在x 轴和y轴上的焦点坐标，θ为参数。
4. 极坐标方程：双曲线的极坐标方程为r^2 = a^2·sec^2θ - b^2·tan^2θ。
其中，a和b分别为双曲线在x轴和y轴上的焦点坐标，θ为参数。
二、双曲线的性质1. 对称性：双曲线关于x轴和y轴均对称。
2. 渐近线：双曲线有两条渐近线。
两条渐近线的夹角等于双曲线的离心率e的反正切值。
第一条渐近线的斜率为b/a，第二条渐近线的斜率为-b/a。
3. 凹凸性：双曲线的两个分支分别为凹曲和凸曲。
4. 渐进性质：当x趋于正无穷时，双曲线的y趋于无穷；当x趋于负无穷时，双曲线的y 趋于无穷。
当y趋于正无穷时，双曲线的x趋于无穷；当y趋于负无穷时，双曲线的x趋于无穷。
5. 双曲线的离心率e的物理意义：离心率e表示焦距和直距的比值，即e=c/a。
其中，c 为焦点之间的距离，a为双曲线在x轴上的焦点坐标。
6. 双曲线的离心率与点到焦点的距离的关系：双曲线上任意一点P到两个焦点F1和F2的距离之差等于一个常数2a。
即|PF1 - PF2| = 2a。
三、双曲函数1. 双曲正弦函数：sinh x = (e^x - e^(-x))/2，定义域为x∈R，值域为y>0。
2. 双曲余弦函数：cosh x = (e^x + e^(-x))/2，定义域为x∈R，值域为y≥1。
3. 双曲正切函数：tanh x = sinh x / cosh x = (e^x - e^(-x))/(e^x + e^(-x))，定义域为x∈R，值域为y∈(-1, 1)。
一、函数与极限
7、双曲函数及反双曲函数
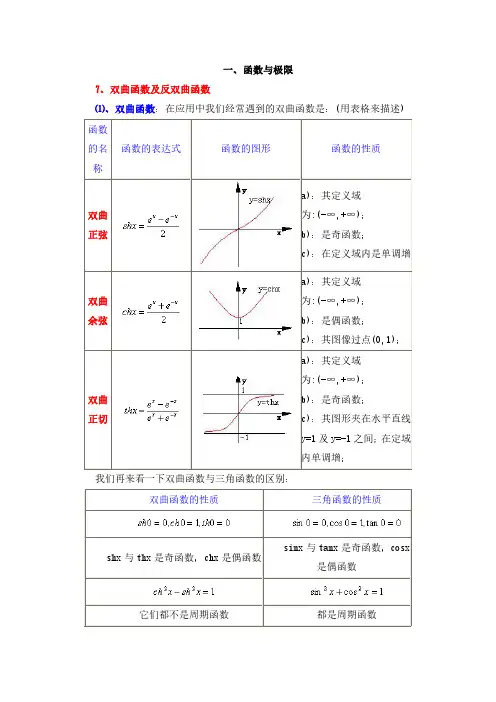
⑴、双曲函数：在应用中我们经常遇到的双曲函数是：(用表格来描述)
函数的名称
函数的表达式
函数的图形
函数的性质
双曲正弦
a)：其定义域
为:(-∞,+∞)；b)：是奇函数；c)：在定义域内是单调增双曲
余弦
a)：其定义域
为:(-∞,+∞)；b)：是偶函数；c)：其图像过点(0,1)；双曲正切
a)：其定义域为:(-∞,+∞)；
b)：是奇函数；c)：其图形夹在水平直线y=1及y=-1之间；在定域内单调增；
我们再来看一下双曲函数与三角函数的区别：
双曲函数的性质
三角函数的性质
shx 与thx 是奇函数，chx 是偶函数
sinx 与tanx 是奇函数，cosx
是偶函数
它们都不是周期函数都是周期函数
双曲函数也有和差公式：
⑵、反双曲函数：双曲函数的反函数称为反双曲函数.
a)：反双曲正弦函数其定义域为：(-∞,+∞)；
b)：反双曲余弦函数其定义域为：[1,+∞)；
c)：反双曲正切函数其定义域为：(-1,+1)；。
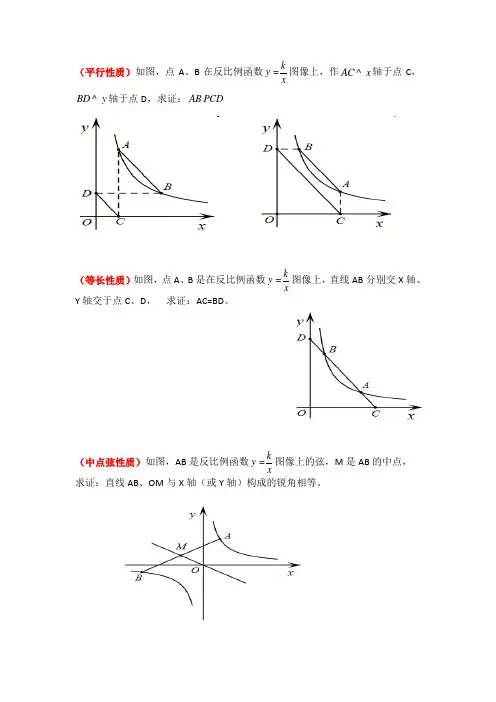
（平行性质）如图，点A、B在反比例函数
k
y
x
=图像上，作AC x
^轴于点C，
BD y
^轴于点D，求证：AB CD
（等长性质）如图，点A、B是在反比例函数
k
y
x
=图像上，直线AB分别交X轴、
Y轴交于点C、D，求证：AC=BD。
（中点弦性质）如图，AB是反比例函数
k
y
x
=图像上的弦，M是AB的中点，
求证：直线AB、OM与X轴（或Y轴）构成的锐角相等。
（直径性质）如图，P 、A 、B 是反比例函数k y x
=图像上的点，且A 、B 关于原点对称，
求证：PA 与PB 与X 轴（或Y 轴）构成的锐角相等。
（平四性质）如图，ABCD 中，A 、B 是反比例函数k y x
=图像上的点，点C 、D 分别x 轴，y 轴上
求证：ABCD 任意两边所在的直线与X 轴（或Y 轴）构成的锐角相等。
