下载文档原格式
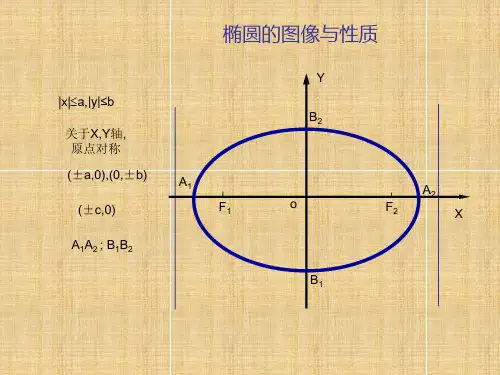
我们所熟知的三角函数也被叫做circular function，因为sin、cos满足 \sin^2x+\cos^2 x=1 可以看出是从一个单位圆的方程 x^2+y^2=1 中演化过来的。
而圆锥曲线我们知道还有双曲线、抛物线、椭圆等，那么其他圆锥曲线是否也可以演化出类似的函数出来？是有的，比如今天介绍的双曲函数，是从单位双曲线方程 x^2-y^2=1 中演化出来的。
先回忆一下三角函数有哪些：sin 正弦，cos 余弦，tan 正切， sec 正割，csc(cosec) 余割，cot 余切详细关系见下图：那么我们的双曲函数也有这些函数，这不过就是在上面六个三角函数后加一个“h”，表示“hyperbolica”，双曲的...一、函数定义sinh 双曲正弦，cosh 双曲余弦，tanh 双曲正切， sech 双曲正割，csch(cosech) 双曲余割，coth 双曲余切接下去是各个双曲函数的表达式：二、函数图像下面是各个双曲函数的图像以及对应定义域、值域等：y=\sinhx=\frac{e^x-e^{-x}}{2}2. y=\cosh x=\frac{\mathrm{e}^{x}+\mathrm{e}^{-x}}{2}3. y=\tanhx=\frac{\mathrm{e}^{x}-\mathrm{e}^{-x}}{\mathrm{e}^{x}+\mathrm{e}^{-x}}4. y=\operatorname{sech}x=\frac{1}{\operatorname{cosh}x}=\frac{2}{\mathrm{e}^{x}+\mathrm{e}^{-x}}5. y=\operatorname{cosech} x=\frac{1}{\sinh x}=\frac{2}{\mathrm{e}^{x}-\mathrm{e}^{-x}}6. y=\operatorname{coth} x=\frac{1}{\tanhx}=\frac{\mathrm{e}^{x}+\mathrm{e}^{-x}}{\mathrm{e}^{x}-\mathrm{e}^{-x}}三、几何意义从上面这张图中能看出来双曲函数自变量的几何意义，是红色所围成面积的两倍，或者看下图也是一样的：那么与三角函数之间的关系呢？四、双曲恒等式我们知道三角函数有非常多的恒等式，这也是三角函数成为高中生噩梦的很大一部分原因，如果不清楚有哪些恒等式可以点击下文：那么类似的，双曲函数也有很多恒等式，并且可以这么说在三角函数中有的恒等式，在双曲函数中都有类似的，下面给出了一些当然这些恒等式我们都是可以证明的，比如高数书上就给了两个例子：所以给出恒等出我们都可以通过sinh、cosh定义带入进行计算，可能计算上会有一点复杂。
