下载文档原格式
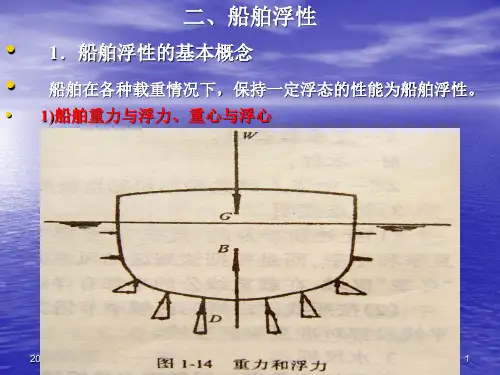
浮体与潜体的稳定性分析在浮岛、渔礁的实际工作状态中，他们的稳定性是很重要的。
浮岛是浮在水面上要稳，渔礁是下沉过程和浮在水中两种状态要稳定，下沉过程过多的翻滚容易造成沉底时的撞击位置不对收到破坏，这边从浮体和潜体的受力情况进行分析并进行总结。
1、浮体的几个力学概念重心：重力的合力作用点浮心：浮力的合力作用点，取为排开水体部分的重心稳心：船舶浮心曲线的曲率中心，船正浮时的浮力作用线与非正浮时的浮力作用线的交点。
首先稳心是个交点——两条浮力作用线的交点——正浮状态下和非正浮状态下两条浮力作用线的交点。
浮心不能太高，太高时，船舶摇摆周期会缩短，让在船舶上的人员乘坐很不舒服,因此船底做成弧形成不是宽扁形状，这样稳心会比较低。
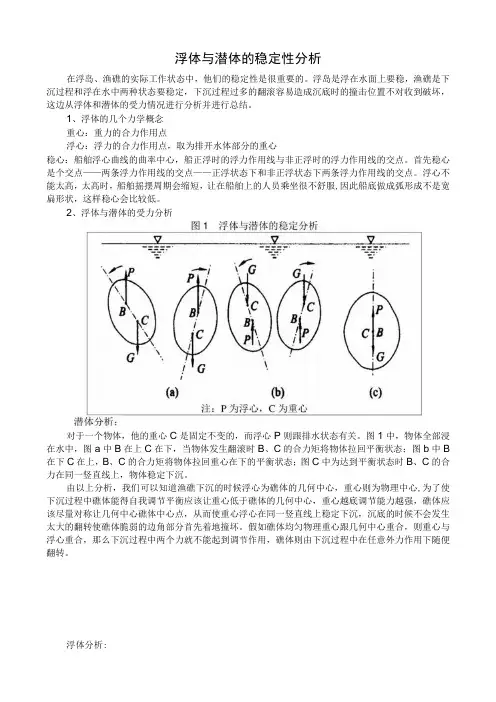
2、浮体与潜体的受力分析对于一个物体，他的重心C是固定不变的，而浮心P则跟排水状态有关。
图1中，物体全部浸在水中，图a中B在上C在下，当物体发生翻滚时B、C的合力矩将物体拉回平衡状态；图b中B 在下C在上，B、C的合力矩将物体拉回重心在下的平衡状态；图C中为达到平衡状态时B、C的合力在同一竖直线上，物体稳定下沉。
由以上分析，我们可以知道渔礁下沉的时候浮心为礁体的几何中心，重心则为物理中心,为了使下沉过程中礁体能得自我调节平衡应该让重心低于礁体的几何中心，重心越底调节能力越强，礁体应该尽量对称让几何中心礁体中心点，从而使重心浮心在同一竖直线上稳定下沉，沉底的时候不会发生太大的翻转使礁体脆弱的边角部分首先着地撞坏。
假如礁体均匀物理重心跟几何中心重合，则重心与浮心重合，那么下沉过程中两个力就不能起到调节作用，礁体则由下沉过程中在任意外力作用下随便翻转。
浮体分析:图2浮体受力图重心位置：重心位置影响平衡的状态，如图，当船受外边影响的时候，船会向一边倾斜（如向边倾斜），那么浮心也会向右倾斜，而重心是不弯的，浮心和重心上两边的合力矩将船身拉回平衡状态使浮力重心在同一竖直线上，因此，船体的重心最好是不变的，不然船体受影响倾斜后，重心改变，回力合矩重新拉回的平衡状态将与新的重心平衡，从而达不到原本理想的平衡状态（如在浮岛铁盒内放水，倾斜后水往一边跑，重心改变了，重新平衡后船体还是斜的）。
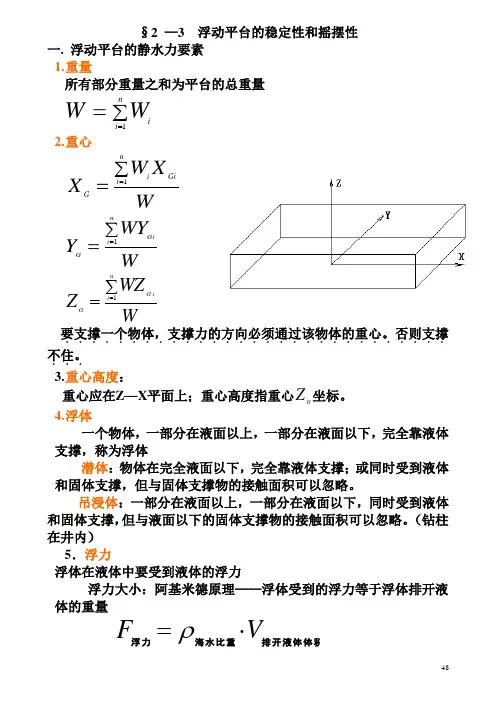
§2 —3 浮动平台的稳定性和摇摆性一. 浮动平台的静水力要素 1. 重量所有部分重量之和为平台的总重量∑==ni iW W 12. 重心WXW X ni GiiG∑==1WWYY ni GiG∑==1WWZZ ni iG G∑==1要支撑一个物体，支撑力的方向必须通过该物体的重心。
否则支撑．．．．．．．．．．．．．．．．．．．．．．．．．．．．．不住。
．．．3. 重心高度：重心应在Z —X 平面上；重心高度指重心G Z 坐标。
4. 浮体一个物体，一部分在液面以上，一部分在液面以下，完全靠液体支撑，称为浮体潜体：物体在完全液面以下，完全靠液体支撑；或同时受到液体和固体支撑，但与固体支撑物的接触面积可以忽略。
吊浸体：一部分在液面以上，一部分在液面以下，同时受到液体和固体支撑，但与液面以下的固体支撑物的接触面积可以忽略。
（钻柱在井内） 5．浮力浮体在液体中要受到液体的浮力浮力大小：阿基米德原理——浮体受到的浮力等于浮体排开液体的重量排开液体体积海水比重浮力VF ⋅=ρ浮力的作用线必然通过浮体的重心 6．浮心浮力的作用点为浮心，位置在排开液体体积的形心 7.浮轴正浮状态下浮心与重心的连线称为浮轴， 浮体的浮心和重心在一条铅垂线上时，称为正浮状态；8.水线，浮面，漂心浮体与水面的交线，称为水线； 水线围成的面积，称为浮面； 浮面的形心，称为漂心。
如浮面由多个小浮面组成 则∑==ni iSS 1漂心坐标：SXS X ni iiS∑==1；SYS Y ni iiS∑==1；计算浮面的用处：吃水深度增加z ∆，吃水量增加wZ S Wγ⋅∆⋅=∆9.排水量排开液体的重量，与浮力相等平台上载重↑→总重量↑→排水量↑→吃水深度↑→浮力↑ 吃水深度不同→浮力不同→浮心位置就会不同 10.储备浮力吃水线至水密甲板的距离，称为干舷高度；干舷高度所处平台体积的排水量，称为储备浮力。
储备浮力起安全系数作用，在实际操作中不能动用 二. 钻井平台有关稳定的概念()()⎩⎨⎧否则无法活不能翻船否则无法干不能倾侧过大稳定 1.两种倾侧：浮轴绕X 轴倾侧，称为横倾 ； 浮轴绕Y 轴倾侧，称为纵倾 ；2.六种运动：三种直线运动：进退，横漂，升沉；三种绕轴运动：横摇，纵摇，平摇；3.三种稳性：(1)静稳性在静力作用下平台的稳性称为静稳性静力：作用力是从零逐渐增大到某个值，或从某个值逐渐减小到零。
漂浮物体规律
一、漂浮物体概述
漂浮物体是指在液体或气体介质中，不受外力作用时能够保持浮状态的物体。
一般来说，漂浮物体受到的浮力大于其自身重力，使得物体能够在液体或气体中保持稳定的浮动。
本文将探讨漂浮物体的规律、影响因素以及实际应用。
二、漂浮物体的规律及其应用
根据阿基米德原理，物体在液体中受到的浮力与物体排开的液体体积成正比，比例常数为液体的密度。
公式表示为：F浮= ρ液体V排开g。
在此规律下，我们可以通过调整物体的体积、密度等因素来实现漂浮。
三、影响漂浮物体的因素
1.液体或气体的密度：密度越大，物体受到的浮力越大，实现漂浮所需的物体体积和重量也相应减小。
2.物体形状：物体形状会影响其排开液体或气体的体积，从而影响浮力的大小。
通常情况下，物体越扁平，受到的浮力越大。
3.物体表面粗糙度：表面粗糙度会影响物体与液体或气体之间的摩擦力，进而影响物体的漂浮性能。
四、实际应用案例分析
1.船舶：船舶采用较宽的船体设计，使得船体在水中受到的浮力增大，从而实现漂浮。
同时，船舶采用双层船壳等结构，降低船体自重，提高漂浮性能。
2.气球和飞艇：气球和飞艇利用气体密度较低的原理，使气体充满内部，从而在空气中实现漂浮。
例如，热气球利用加热空气使密度降低，实现自身漂浮。
五、总结与展望
漂浮物体在生活和科学研究中具有广泛的应用价值。
通过掌握漂浮物体的规律，我们可以更好地设计、优化各类漂浮结构，提高其性能。
Research 研究探讨347浮体的平衡与稳定性研究分析王宏飞 曾昕萌 刘 涛 李株丹(华北水利水电大学， 河南 郑州 450046)中图分类号：G322 文献标识码：B 文章编号1007-6344（2018）04-0347-01摘要：在文章中作者对浮体的稳定性和平衡性作了分析讨论，并对定倾中心概念作了简单介绍，并根据以往的案例，对浮体的稳定性进行了研究，直至最后用能量守恒定律的方法对定倾高度和浮体稳定性作了细致的说明，关键词：平衡性；稳定性；浮体；定倾中心0前言人类对浮体的平衡和稳定问题很感兴趣，在古欧洲文明中阿基米德就在其论著中对浮体在液体中的平衡和稳定性作了系统的研究，斯蒂文也曾判定浮体排开液体的重心和浮体的重心应该在一条直线上，但错误判断为排开液体的重心应该在浮体的重心之上，否则就会翻转180度，惠更斯用数学方法对浮体的平衡性和稳定性进行了研究，认为浮体位置发生变化而转换到另外一个位置时，其重心和浮心的高度差将减小。
欧拉和柏努力也都对浮体的稳定和平衡性作过细致的研究，并重新定义了小扰动和力矩恢复的概念，布格则在世界上首次对定倾中心作了定义，在现代科学领域定倾中心已经成为判定浮体稳定和平衡的一个重要参数，并在水利工程设计中得到了大范围的应用。
1浮体的平衡和稳定性分析在实际应用中，在一些科技文献中对定倾中心的概念定义比较模糊，例如，有的科技工作者认为浮体一旦发生细微变化，浮轴和浮力的作用线在一个固定点上相交，也有的科学家认为只有在实验室中上述两条直线才可能在一个固定点上相交；另外，用力系简化方法研究分析定倾高度的方法也不够科学严谨，有人甚至对稳定性的判定条件分析都出现了错判，带着这些问题作者翻阅了大量的中外科技文献，并结合了具体的案例对定倾中心概念作了明确的定义，对浮体的稳定性和平衡性作了判别，最终提出了用定倾高度判定浮体是否稳定的科学依据。
假设浮体的比重一旦低于水的比重，那么就会发生有的物体部分露出水面同时漂浮在水中，满足这些条件这种物体则称为浮体，浮体在水中平衡则要满足两个条件：第一、浮心和浮体的重心的连线和水平面相垂直。
浮力与物体的浮沉稳定性浮力是指在液体或气体中，由于物体与介质之间的压力差异而引起的向上的力。
这个力的大小取决于物体在介质中排开的体积，即物体的体积。
当物体的体积较大时，浮力也相应增加。
而物体的浮沉稳定性则与其相对密度有关。
相对密度越小，物体越容易浮起来。
想要了解浮力与物体的浮沉稳定性，我们首先需要了解什么是相对密度。
相对密度又称比重，是指物体的密度与介质的密度之比。
若物体的相对密度小于1，说明物体的密度小于介质的密度，物体将浮起来；若物体的相对密度等于1，说明物体的密度等于介质的密度，物体将悬浮在介质中；若物体的相对密度大于1，说明物体的密度大于介质的密度，物体将沉没在介质中。
在液体中，物体受到的浮力可以通过阿基米德定律来计算。
阿基米德定律的表达式为：浮力 = 排开的液体体积 ×液体的密度 ×重力加速度根据阿基米德定律，物体受到的浮力与物体在液体中排开的体积成正比。
也就是说，物体的体积越大，受到的浮力越大。
这也是为什么大型船只可以浮在水面上的原因。
船只的体积较大，因此受到的浮力也较大，使得船只能够在水中浮起来。
另外，物体受力的平衡也会影响物体的浮沉稳定性。
如果物体在介质中处于不平衡状态，就会发生浮力和重力不平衡的情况，导致物体倾斜或翻转。
为了保持物体的稳定性，我们可以通过改变物体的形状或调整物体在介质中的位置来实现。
举个例子来说，当我们在水中放入一个空心的球体，球体会因为浮力的作用而上浮，但是球体有可能因为上浮不稳而发生倾斜。
如果我们在球体底部加重物，球体的重心会下移，使得其更加稳定，不易倾斜。
总之，浮力和相对密度是影响物体浮沉稳定性的重要因素。
物体的体积越大，受到的浮力越大，物体浮起的可能性也就越大。
而相对密度越小，物体越容易浮起来。
此外，物体的形状和位置也对浮沉稳定性有一定的影响。
为了保持物体的稳定，我们可以通过调整物体的重心位置或改变物体的形状来实现。
关于浮体的平衡与稳定性)1谢建华(西南交通大学牵引动力国家重点实验室)摘要：本文讨论了浮体的平衡与稳定问题，介绍了定倾中心的定义，并结合一个具体的例子，给出了定倾高度的三种不同的计算方法，最后，根据能量方法说明了用定倾高度判定浮体稳定性的理论依据。
关键词：浮体；平衡；稳定性浮体的平衡与稳定问题研究是一个非常有实际意义的课题，是船舶与海洋平台设计的理论基础，在其它工程中也有广泛的应用。
在浮体稳定性研究中，定倾中心是一个重要的概念，但是，笔者认为有一些教科书或文献对此概念的定义是不够明确的，例如，有的认为，当船体发生微小摇晃时浮力的作用线交对称轴线（浮轴）于一定点，此点即为定倾中心]2[],1[，也有的认为实验表明前述两直线交于一点]3[。
另外，在用力系简化方法推导定倾高度的过程中也有含糊不清之处]1[，或在稳定性判定上发生错误]4[。
笔者带着这些疑问查阅了若干参考书，特别是[5]、[6]和[7]。
根据这些材料，本文介绍了定倾中心的明确定义，并结合一个具体的例子，给出了定倾高度三种不同的计算方法，最后，根据能量方法说明了用定倾高度判定浮体稳定性的理论依据。
如果物体的比重比水小，物体在水中漂浮平衡时，有一部分将露出水面，这样的物体称为浮体。
浮体要满足以下两个条件才能平衡：(i) 受水的浮力等于浮体的重量；(ii)浮心(浮力的作用点)与浮体重心的连线和水平面垂直，如图1(a)所示。
浮体平衡位置还要满足稳定性条件才能具体实现。
图1(b)表示一个长方形物块平躺和竖立平衡位置发生了微小的扰动，其中，左边的物块上作用的重力和浮力阻碍了物块进一步偏离其平衡位置，因此平衡是稳定，而右边的物块则相反，其上作用的重力和浮力加剧了偏离其平衡位置，平衡是不稳定。
以下来分析浮体平衡和稳定的条件。
图1 浮体的平衡假设浮体有一个对称面，平衡位置发生扰动时，浮体上各点的位移均平行于对称面，浮体作平面运动。
容易说明浮体对铅直和水平扰动是稳定的，仅需考虑浮体对转动方向扰动的稳定性问题。
平衡时，浮体与水平面的交面称浮面，记为S。
先建立一个与浮体固连的坐标)1国家自然科学基金资助项目(10772151)系z y Ox 00：取浮面的形心O 为坐标系原点，浮面与对称面的交线称为浮线，取其为0x 轴， 浮轴0y 铅直向上， z 轴在浮面内并于0x 和0y 轴正交，如图2所示。
浮体绕O 点(Oz 轴)转动微小角度θd 时，与浮体固连的坐标系z y Ox 00变成了Oxyz 。
设平衡时，浮体重心0C 和浮心0D 在与y 轴平行的直线上，此直线交x 轴于N 点，设c ND =0，e NO =，d D C =00。
考虑积分0000000⎰⎰⎰⎰==SS dy dx x d dy dx d x θθ (1) 因为z 轴是通过S 形心的主轴，故(1)成立。
即当绕z 轴作微小转动时，浮体排开水的体积不发生变化，随之其受到的浮力大小不变。
图2 浮心与定倾中心平衡位置发生微小转角之后，浮体浸入水中部分的形状发生了变化，浮力的作用点位置随之改变，浮心相对浮体由0D 点移至D 点，其相对浮体的轨迹是xy 平面过0D 和D 点的平面曲线，称其为浮心曲线(curve of buoyancy)。
杜宾(Dupin)第一定理表明]6[，过D 点的水平线是浮心曲线在该点切线，因此浮力F 作用线是浮心曲线在该点的法线，于是当D 点无限趋近0D 点时，浮力F 作用线与浮轴y 交点M 趋近位于轴y 的一个定点，该点称为定倾中心(metacentre)。
定倾中心即为浮心曲线在0D 点处的曲率中心。
当发生微小转角θd 时，浮力F 作用线与浮轴y 的交点M 在定倾中心的充分小邻域内，有时又称M 为定倾中心。
如图1(b)，若定倾中心M 位于浮体重心0C 之上，重力和浮力形成了一个“恢复”力偶，浮体的平衡是稳定的；反之，若定倾中心M 位于浮体重心0C 之下，重力和浮力形成了一个“排斥”力偶，浮体的平衡是不稳定的。
对某个平衡位置而言(图2)，定倾中心M 与浮体重心0C 的高度差h 称为定倾高度(metacentre hight)。
当0>h 时，浮体的平衡是稳定的；当0<h 时，浮体的平衡是不稳定的。
如图2所示，以0D 为坐标原点，建立直角坐标系110y x D ，其中1x 轴和1y 轴分别与x 轴和y 轴平行且指向分别相同，计算D 点的坐标如下]5[：θθd VI V dxdy xd x e V x Z S D -=+-+⋅=⎰⎰))((01 (2) 21)(2))(2/(0θθθd V I V dxdy xd xd c V y Z SD =--+⋅=⎰⎰ (3) 其中Z I 是平衡时的浮面S 对z 轴的惯性矩，V 是浮体排开水的体积。
由(2)和(3)式，θd VI ds Z = (4) 其中ds 是浮心曲线上由D 到0D 的弧长。
于是VI d ds M D Z ===θρ0 (5) d V I d h Z -=-=ρ (6) 其中ρ是浮心曲线在0D 点处的曲率半径。
例1]5[],1[ 如图3(a)所示，一根横截面为正方形的长木块漂浮于水面上，试确定其平衡位置稳定性。
已知木块和水的比重分别为木μ和水μ，木块的相对密度为水木μμ/=s 。
图3水中漂浮的木块解法一：设木块平衡时吃水深度为b ，由平衡条件木水μμl a l ab 2)2()2(= (7) 由(7)，得：as b 2= (8) 有关量计算如下：)1(22/00s sb b a D C d -=-== (9) 2312)2(12)2(/s b abl l a V I z ===ρ (10) 由(6))166(1222+-=-=s s sb d h ρ (11) 令0=h ，由(11)解出：7886.06/32/1,2113.06/32/121≈+=≈-=s s 。
因此，当2113.0<s 或7886.0>s 时，平衡是稳定的；当7886.02113.0<<s 时，平衡是不稳定的。
容易证明，如将s 换成s s -='1，并将木块的某一个平衡位置沿浮面反射，木块仍保持平衡，而且稳定性不变，因此可设2/1≤s ]6[],5[。
解法二：先求出浮心曲线的表达式，然后确定此曲线在平衡时浮心处的曲率半径。
为此，建立与浮体固连的直角坐标系xy C 0，如图3(b)所示。
可计算出浮心D 的坐标：θtan 6sa x D -= (12) θ2tan 12)1(sa s a y D +--= (13) 浮体平衡条件(ii)为：θtan D D y x = (14) 将(12)、(13)代入(14)中，得：{}02)1(12tan tan 122=+--s s s a θθ (15) 由(15) 知浮体有平凡的平衡位置：)0(tan 0==θθ (16)及可能有非平凡的平衡位置：)166(2tan 22+--=s s θ (17)由(12)和(13)消去θ，得： 23)1(D D x as s a y +--= (18) 可见浮心曲线是顶点在))1(,0(s a --点处、开口向上的抛物线。
在0D 处的曲率半径为sa y y D x D D 6)1(02/32='''+==ρ (19) 于是)166(12)1(2622+-=--=-=s s sb s s b s a d h ρ (20) 显然(20)与(11)相同。
由(17)和(20)可知，当平凡解0=θ不稳定时，有非平凡解0≠θ存在。
解法三：在(12)和(13)中，记θtan =t 及2222D D CD y x d u a +==，则222212)1(36⎭⎬⎫⎩⎨⎧--+=s t s s t u (21) {}2)1(123622+--=s s t s t dt du (22) {}2)1(1233612222+--=s s t s dt u d (23) 令0/=dt du ，得到与(15)等价的方程。
将平凡平衡位置0=t 代入(23)，令0/22>dt u d 可解出2113.0<s ；将非平凡的平衡位置(17)代入(23)，有018//2222>=s t dt u d 。
因此，对平凡平衡位置0=t ，当2113.0<s 时，浮体重心到浮心的距离是极小值，平衡是稳定的；当2113.0>s 时，浮体重心到浮心的距离是极大值，平衡是不稳定的。
图4尖点奇异性浮心曲线(18)是对应正方形有两个顶点浸入水中情况的，由图3(b)，此时要满足条件s a b 2/tan =≤θ (24) 将(24)代入(17)，可得25.04/1=<s ，正方形有两个顶点浸入水中的平衡位置存在范围为25.00<<s 。
当正方形有两个顶点浸入水时，浮心曲线是一抛物线，如图4所示，渐屈线(曲率中心的轨道)Γ有一个尖点0M 。
浮体的重心0C 到浮心曲线任一条法线对应一个平衡位置，如图4(a)中的法线0l 与4 (b)中的 0l 和1l 。
浮体摇晃运动类似于与刚体固连的浮心曲线H 在某一水平线L 上作纯滚动(L 的高度是变化的)。
对某一平衡位置而言，如果浮体的重心在浮心之定倾中心之间，如图4(a)中的平衡位置0l ，那么0C 到0M 的距离是极小值，浮体的势能(含排开水的势能)为极小值，于是平衡是稳定的；如果浮体的重心在浮心和定倾中心之外，如图4(b)中的平衡位置0l ，那么0C 到0M 的距离是极大值，浮体的势能为极大值，于是平衡是不稳定的]5[。
当平衡位置0l 不稳定时，木块就转换到新的稳定平衡位置1l 上，在水中倾斜了。
如果记浮体浮心和重心距水表面深度分别为D h 、C h ， W 是浮体的重量。
浮体将其排开的水挤压到水的自由表面上，故其势能为)(C D C D h h W Wh Vh -=-水μ (25) 如果记CD d 为浮体的重心到浮心的距离，可证明0)(=-C D h h δ与0=CD d δ等价，以及)(2C D h h -δ与CD d 2δ同号，即浮体势能的每个极值点对应浮体的一个平衡位置，浮体势能的极小值对浮体稳定的平衡位置，而极大值对应不稳定的平衡位置]5[。
浮心曲线是一条封闭曲线，例如，长方形木块的浮心曲线是四段抛物线和四段双曲线相间连接而成]7[，浮体重心到浮心曲线的每个法线确定一个平衡位置，此时浮体重心到浮心距离为极值，因此任何浮体总存在一个稳定和一个不稳定的平衡位置，稳定平衡位置与不稳定总是相互隔离的。
可以证明一般n 边形最多可能有n 4个平衡位置，例如，正三角形最多可能有12个平衡位置]6[。
以上讨论的仅是平面浮体的平衡问题，如果是像海洋平台之类的三维浮体的平衡问题的话，那么就更复杂了。
