当前位置：文档之家 › 曲面立体表面点的投影

曲面立体表面点的投影

  • 格式：docx
  • 大小：199.89 KB
  • 文档页数：10

下载文档原格式

  / 10

合集下载

基本体的投影----立体表面上点的投影

基本体的投影----立体表面上点的投影
教学重点难点
重点是图线画法和尺寸标注；平面图形的尺寸分析、线段分析以及圆弧连接的画法；难点是尺寸标注，平面图形的尺寸分析
教学方法
多媒体课件讲授实际演示，提问启发
教学用具
三角板直尺
教学过程设计
教学内容
师生活动
平面立体的投影
一、棱柱
1、棱柱的投影
如下图，是一六棱柱，它是由上下两正六边和六个矩形的侧面所围成。对各投影进行分析。
教案
授课教师
王晓萍
课次
课时
2
授课班级
08机电
职称
周次
课型
授课日期
教材名称和版本
课题
2-3基本体体的投影
教学目标
本讲主要介绍与工程制图有关的国家标准，如图纸的幅面和格式、比例、字体、图线和尺寸标注等，介绍了绘图仪器的使用方法和平面图形的绘制步骤。要求掌握正确的作图方法和正确地使用绘图工具，在绘制的图样中遵守国家标准《机械制图》和《技术制图》中的各项规定。
作投影图时，先画出中心线对称线，再画出六棱柱的水平投影正六边形，最后按投影规律作出其它投影。
教学过程设计
教学内容
师生活动
正六棱柱的投影及表面上取点
2．棱柱表面上取点
1）棱柱表面都处于特殊位置，其表面上的点可利用平面的积聚性求得；
2）求解时，注意水平投影和侧面投影的Y值要相等；
3）点的可见性的判断，面可见，点则可见，反之不可见。
圆球表面上取点
作业内容
参考资料
教材
（1）辅助素线法，如图（b）。
五、球
1．球的形成
球面可看成是以一圆为母线，以其直径为轴线旋转而成。
2．球的投影
圆球的投影是与圆球直径相同的三个圆，这三个圆分别是三个不同方向球的轮廓的素线圆投影，不能认为是球面上同一圆的三个投影。对投影图进行分析。

基本立体的投影及其表面取点

基本立体的投影及其表面取点
因点M所在表面△SAB为一般位置平面，所以可以利用辅助线法来
作图。
(a)
图3.5 正三棱锥表面取点
(b)
方法一：过M点在△SAB上作AB的辅助平行线ⅠM，即1’m’‖a’b’，再作1m‖ab，求出m， 再根据m、m求出m″（如图3.5a）所示；
方法二：过锥顶S和点M作一辅助线SⅡ，然后求出点M的水平投影m（如图3.5b）。 可见性判断：同棱柱。
2.圆锥 (1) 圆锥的形成 如图3.8a可知，圆锥的表面由圆锥曲面和底面圆组成。圆锥面可以看成是一直线OA绕与 其相交的轴线OO1旋转而成。圆锥面上通过锥顶S的任一直线都是圆锥面的素线。
(a) (c)
(b) 图3.8 圆锥的投影
(2)投影分析 由图3.8b可知，底面平行于H面的圆锥，其正面投影和侧面投影
(3)画法 首先画出圆柱在各个投影位置上的轴线和底圆的对称中心线，其 次画出投影为圆的圆的视图——俯视图，最后根据圆柱高及投影的 外形轮廓素线画出其余两个视图。注意：绘制回转体投影时，必须 画出轴线和对称中心线。根据国家标准的规定，轴线和对称中心线 应采用细点画线画出，且要超出轮廓线2～5 mm，如图3.6c所示。 (4)圆柱表面上取点 轴线处于特殊位置的圆柱，其圆柱面在与轴线垂直的投影面上的
1.2曲面立体的投影及其表面上取点 表面均为曲面，或由曲面和平面共同围成的基本立体称为曲面立体。常见的曲面立体多为
回转体。回转体是由一母线（直线或曲线）绕以固定的轴线ห้องสมุดไป่ตู้回转运动所形成。常见的回 转体包括圆柱、圆锥、圆环和球等。
1.圆柱 （1）圆柱的形成 圆柱体表面是由圆柱面和上下两圆形底面所组成。圆柱面可以看成是由直线AA1绕与它平 行的轴线OO1旋转而成的回转面，如图3.6a所示。直线AA1为母线，它在圆柱面上任一位 置称为素线。

曲面立体的投影

曲面立体的投影

线上，如图4-13(b)所示。因圆柱水平投影具有积聚性，
所以这三点的水平投影一定都在圆上，根据其位置判断
可见性即可，再根据三等关系即可求出侧面投影。
Page 22
单击此处编基辑母本版体标的题样投式影
曲面立体的投影
Page 23
作图步骤如下：点a′为可见点，根据点a′的位置分析，其侧面投影 位于前轮廓线素线上，可过点a′作水平线交前轮廓素线于一点(即a″点)， 根据三等关系可求出水平投影a。同理，c′点位于右轮廓素线上，根据 水平投影的积聚性，从c′点向圆柱水平投影作垂线交于一点即为c点， 根据三等关系可求出点c″的位置，其侧面投影为不可见点，需要用小 括号括起来。b′点位于后左平面上，根据水平投影的积聚性，从b′点向 圆柱水平投影作垂线交于一点即为b点，再根据三等关系可求出点b″的 位置。
单击此处编基辑母本版体标的题样投式影
曲面立体的投影
1.素线法 圆锥面由许多素线组成，圆锥面上任一点必在经过该点的素线 上，因此只要求出过该点素线的投影，即可求出该点的投影。 2.纬圆法 由回转面的形成可知，母线上任一点的运动轨迹为圆，且该圆 垂直于旋转轴线，这样的圆称为纬圆。圆锥体上任一点一定在与其 等高的纬圆上，因此可借助该点的纬圆求出该点的投影。
曲面立体的投影
2.投影分析 （1）俯视图。俯视图为一个圆，其投影的轮廓线是球的 最大水平面①的投影。球被分为上、下两部分，上部分可见， 下部分不可见。 （2）主视图。主视图为一个圆，其投影的轮廓线是球的 最大正平面②的投影。球被分为前、后两部分，前部分可见， 后部分不可见。 （3）左视图。左视图为一个圆，其投影的轮廓线是球的 最大侧平面③的投影。球被分为左、右两部分，左部分可见， 右部分不可见。
Page 29

机械制图教案——第3章 立体的投影

机械制图教案——第3章 立体的投影

第3章立体的投影一、本章重点：1.平面立体和曲面立体投影的画法，及立体表面点的投影。

2.立体与平面相交其交线的画法，既求截交线。

3.两回转体轴线垂直相交其交线的画法。

4.立体的尺寸标注。

二、本章难点：1.圆球和圆环的投影及表面上点的投影。

2.圆锥、圆球被平面截切后，截交线的画法。

3.求作相贯线。

三、本章要求：通过本章的学习，要掌握基本体的三面投影画法，基本体表面点的投影，能够分析和绘制常见的截交线和两回转体轴线相交时的相贯线，掌握立体的尺寸标注的方法。

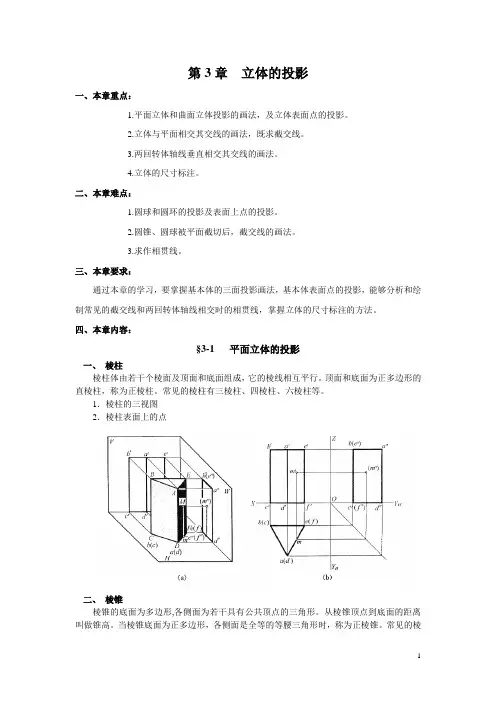
四、本章内容：§3-1 平面立体的投影一、棱柱棱柱体由若干个棱面及顶面和底面组成，它的棱线相互平行。

顶面和底面为正多边形的直棱柱，称为正棱柱。

常见的棱柱有三棱柱、四棱柱、六棱柱等。

1．棱柱的三视图2．棱柱表面上的点二、棱锥棱锥的底面为多边形,各侧面为若干具有公共顶点的三角形。

从棱锥顶点到底面的距离叫做锥高。

当棱锥底面为正多边形，各侧面是全等的等腰三角形时，称为正棱锥。

常见的棱锥有三棱锥、四棱锥、六棱锥。

1. 棱锥的三视图2．棱锥表面上的点§3-2曲面立体的投影曲面立体的表面是由一母线绕定轴旋转而成的，故称曲面立体，也称为回转体。

常见的回转体有圆柱、圆锥、圆球和圆环等。

一、圆柱1．圆柱面的形成圆柱面可看作一条直线AB围绕与它平行的轴线OO回转而成。

OO称为回转轴，直线AB称为母线，母线转至任一位置时称为素线。

这种由一条母线绕轴回转而形成的表面称为回转面，由回转面构成的立体称为回转体。

2．圆柱的三视图3．圆柱表面上的点二、圆锥1．圆锥面的形成圆锥面可看作由一条直母线围绕和它相交的轴线回转而成。

2．圆锥的三视图3．圆锥表面上的点三、圆球1．圆球面的形成圆球面可看作一圆（母线），围绕它的直径回转而成。

2．圆球的三视图3．圆球表面上的点四、圆环1．圆环的形成圆环面可看作由一圆母线，绕一与圆平面共面但不通过圆心的轴线回转而成。

图中的回转轴是铅垂线。

建筑工程制图第4章 曲线与曲面立体的投影

建筑工程制图第4章 曲线与曲面立体的投影

两圆柱位置不同时相贯线的变化趋势
(a)
(b)
(c)
(d)
4.5 旋转楼梯
平螺旋面
螺旋楼梯
4.5 旋转楼梯
1．平螺旋面
4.5 旋转楼梯
平螺旋面的应用— 螺旋楼梯
4.5 旋转楼梯
平螺旋面的应用— 螺旋楼梯
4.5 旋转楼梯
4.5 旋转楼梯
Thanks
5 3
4.3 平面与曲面立体截交
例3:圆锥被正平面截切，补全主视图。Fra bibliotek● ●
e′
●
c d′
′
●
●
a′
b′
截交线 的空间 E 形状？ 截交线 D C 的投影 特性？ A
B
a c
●
●
●
e
●
d
●
b
4.3 平面与曲面立体截交
例4:圆锥被正平面截切，补全主视图。
● ●
e′
●
c d′
′
●
●
a′
b′
截交线 的空间 E 形状？ 截交线 D C 的投影 特性？ A
底圆 母线 素线 顶圆 轴线
4.2 曲面立体及其表面上的点
例1：绘制圆柱的三视图。 O A
O1 A1
4.2 曲面立体及其表面上的点
例2：已知圆柱表面的点的投影1’、2’、3’、4，求其它两面投影。
4
1′


4″
1″


3

(2)

2″

3
利用投影的
积聚性 O A
2 1


4


3
O1 A1
相贯线 相贯线

曲面体投影及其表面上点投影作图

曲面体投影及其表面上点投影作图
求曲面体表面上点的投影:先分析这个空间点在曲面体的前、后、左、右、上、下哪半个部 分上，是可见的还是不可见的， 然后再展开找点的投影，方法有辅助素线法，辅助纬圆法，先作 出辅助素线或辅助纬圆的三个投影，再在辅助素线或纬圆上找点的投影。
工程上常见的零件形体多数具有立体被平面切割所形成 的截交线，或两立体相交而形成的相贯线、为了更好地正确、 快捷绘制好汽车零件、部件图; 有必要学习基本几何体的投 影画法，立体表面上点的投影作图、截交线和相贯线的画法。
学习目标
1 项目描述
1
(１)学习基本几何体的投影及立体表面上点、线的投影；
知识
2
13 知 识 准 备
三 圆球
圆球面可看作为由一条圆母线绕其直径回转而成，如常见的蓝球、足球、排球等。 １. 投影分析
圆球的三面投影都是圆，直径与球直径相等，如图 3-16所示。
13 知 识 准 备
三 圆球
主视图的投影是圆，它是圆球面前半部分与后半部分的分界线，而且在俯视图和左视图投 影都为中心线，前半部分可见，后半部分不可见。
如在图Ａ３４-1图1 幅所上示按：补１画∶三１视的图比，例并绘作制出支立架体零表 面件上平点面Ｍ轮、廓Ｎ图形的，另如两图个投１影￣。７ 所示。
图 3-11 补画三视图
2 任务目标
1 能画出曲面体的三面投影视图。 2 能作出曲面体表面上点的投影。
建议学时：2学时。
13 知 识 准 备
一 圆柱
常见的曲面立体是回转体，就是表面有回转曲面的立体。 曲面体常见的有圆柱、圆锥、圆 环和圆球。 曲面立体的投影，实质上是构成该体的所有表面的投影总和。
《汽车机械制图》
1 平面体投影及其表面上点投影作图 基曲面体投影及其表面上点投影作图 2 3 体立体表面交线绘制

立体表面上点的投影

立体表面上点的投影
图3－6用辅助线法在圆锥面上取点
边画图边讲解作图方法与步骤。
作法二：辅助圆法如图3－7<a）所示，过圆锥面上点M作一垂直于圆锥轴线的辅助圆，点M的各个投影必在此辅助圆的相应投影上。在图3－7<b）中过m′作水平线a′b′，此为辅助圆的正面投影积聚线。辅助圆的水平投影为一直径等于a′b′的圆，圆心为s，由m′向下引垂线与此圆相交，且根据点M的可见性，即可求出m。然后再由m′和m可求出m″。
教案重点
圆锥体和圆球体的三视图画法及表面取点、取线的作图方法
教案难点
在圆球体表面取点、取线的作图方法
教案内容、方法及过程
教案方法：用教案模型辅助讲解。
教案过程：
一、课前提问
1、棱柱、棱锥投影分析和投影特征以及表面求点的方法。
2、圆柱体的投影分析和投影特征以及表面求点的方法。。
二、引入新课题
上次课我们学习了平面立体和圆柱体的投影及表面求点，本次课我们继续学习其他几种曲面立体的投影及表面求点。
<a）<b）<c）<d）
<e）<f）<g）
图3－10平面立体的尺寸注法
2、曲面立体的尺寸标注
圆柱和圆锥应注出底圆直径和高度尺寸，圆锥台还应加注顶圆的直径。直径尺寸应在其数字前加注符号“φ”，一般注在非圆视图上。这种标注形式用一个视图就能确定其形状和大小，其他视图就可省略，如图3－11<a）、<b）、<c）所示。
作法一：辅助线法如图3－6 <a）所示，过锥顶S和M作一直线SA，与底面交于点A。点M的各个投影必在此SA的相应投影上。在图3－6<b）中过m′作s′a′，然后求出其水平投影sa。由于点M属于直线SA，根据点在直线上的从属性质可知m必在sa上，求出水平投影m，再根据m、m′可求出m″。

曲面立体及其表面上点和线的投影

曲面立体及其表面上点和线的投影

水平投影和侧面投影均可见；N点的正面投影不 可见，且在点画线的右侧，由此可判定N点在右、
（a）已知条件
后半圆柱面上，其水平投影可见，侧面投影不可
见。
作图步骤（参见图4-8（b））：
（1）过m′点向下作铅垂线交圆周的前半部分
于一点，则该点为m；由m′点和m点，即可求出m′′
点，m′′点为可见点。
（2）采用同样的方法，先求出N点的水平投
曲面立体及其轴测投影
4．圆环面上点的投影
圆环表面上的点，可使用纬圆法绘制。例如， 已知环面上K点的正面投影k′，求该点的水平投影的 作图方法如图4-13所示。
第 17 页
图4-13 求环面上点的投影
土木工程制图
（b）作图方法 图4-9 利用“辅助线法”求圆柱表面上线的投影
曲面立体及其轴测投影
第 13 页
2．圆锥表面上点的投影
圆锥底面具有积聚性，其上的点可以直接求出。 圆锥面没有积聚性，其上的点需要用辅助线法才能 求出。按辅助线的类型不同，辅助线法可分为素线 法和纬圆法两种。
【例4-3】已知圆锥面上点A的正面 投影a′，如图4-10（a）所示，求其另 外两面投影。
形，同时也是圆锥面的投影。 ➢ V面和W面投影：均为等腰三角形，且三
角形的底边为圆锥底面的积聚投影。V面 投影中，三角形的左、右两边分别是圆锥 面最左素线SA和最右素线SB的投影（素线 也是转向轮廓线）；W面投影中，三角形 的左、右两边分别是圆锥面最前素线SC和 最后素线SD的投影。
（a）立体图
（b）投影图
圆柱体的侧面投影积聚在圆周上。 ➢ V面投影：为一个矩形。其中，上、下两边线
分别是圆柱上、下底面的积聚投影，左、右两 边线分别是圆柱最左、最右处素线的投影。 ➢ W面投影：为一个矩形。其中，上、下两边线 分别是圆柱上、下底面的积聚投影，左、右两 边线分别是圆柱最后、最前处素线的投影。

曲面立体的投影.

曲面立体的投影.
【例4-6】 如下图所示，已知圆锥面上一点A的正面投影a′，求a、a″。
解：（1）分析
（2）作图
方法二：纬圆法。 【例4-7】 如下图所示，已知圆锥表面上一点A的投影a′，求a、a″。
解：（1）分析 （2）作图
2．圆锥表面上线的投影 作圆锥面上线段的投影的方法：是求出线段上的端点、轮廓线上的点、分界点 等特殊位置的点及适当数量的一般点，并依次连接各点的同面投影。 【例4-8】 如下图所示，已知圆锥表面上的线段AB的正面投影，求其另两面投影。
曲线 线、抛物线等）。 空间曲线：曲线上各点不在同一个平面内（如圆柱螺旋线等）。
（二）曲面
曲面可以看成是由直线或曲线在空间按一定规律运动而形成。
曲面
直线曲面：由直线运动而形成的曲面称为。 曲线曲面：由曲线运动而形成的曲面称为。
回转体是由一母线（直线或曲线）绕一固定轴线作回转运动形成的，因 此圆柱体、圆锥体、球体和环体都是回转体。
圆柱曲面是一条直线 围绕一条轴线始终保 持平行和等距旋转而 成。
母线
圆锥面是一条直线与轴线交于一点始终保持一定夹角旋转而成的。
母线
球面是由一个圆或圆弧线以直径为轴旋转而成。
（三）素线与轮廓线
形成曲面的母线，它们在曲面上的任何位置称为素线。 我们把确定曲面范围的外形线称为轮廓线（或转向轮廓线），轮廓 线也是可见与不可见的分界线。 当回转体的旋转轴在投影体系中摆放的位置合理时，轮廓线与素线重 合，这种素线称为轮廓素线。 在三面投影体系中，常用的四条轮廓素线分别为：形体最前边素线、 最后边素线、最左边素线和最右边素线。
第三章 曲面立体的投影
在建筑工程中，我们会接触到各种形状的建筑物（如：房屋、水塔） 及其构配件（如：基础、梁、柱等）的形状虽然复杂多样，但经过仔细 分析，不难看出它们一般都是由一些简单的几何体经过叠加、切割、或 相交等形式组合而成。

第三章曲线曲面和立体的投影

第三章曲线曲面和立体的投影

曲线的投影
曲线是动点运动的轨迹，也可以说是一系列连续点的集合。 因此，绘制曲线的投影时，只要能作出曲线上一系列点的投 影，并把它们的同面投影依次光滑地连接起来，即得曲线的 投影。这是绘制曲线投影的一般方法。 但是，如能根据曲线的投影特性，预先对曲线投影的形状或 特点作出判断，则可以使图形准确作图简化。现将曲线的主 要投影特性分述如下：
在图示位置时，六棱柱的两 点的可见性规定： 底面为水平面，在俯视图中反映 由于棱柱的表面都是平 若点所在的平面的投影 实形。前后两侧棱面是正平面， 面，所以在棱柱的表面上取 可见，点的投影也可见；若 其余四个侧棱面是铅垂面，它们 点与在平面上取点的方法相 平面的投影积聚成直线，点 的水平投影都积聚成直线，与六 同。 的投影也可见。 边形的边重合。
截交线是一个由直线组成的封闭的平 面多边形。 截交线的每条边是截平面与棱面的交线。 ⒈ 求截交线的两种方法： ★ 求各棱线与截平面的交点→棱线法。 ★ 求各棱面与截平面的交线→棱面法。 ⒉ 求截交线的步骤： 确定截交 ★ 空间及投影分析 线的形状 ☆ 截平面与体的相对位置 ☆ 截平面与投影面的相对位置 ★ 画出截交线的投影 确定截交线 分别求出截平面与棱面的交 的投影特性 线，并连接成多边形。
环面投影可见性的判别
由上向下看，此部分可见
由前向后看，此部分可见
（三）非回转直线面 1、柱面
（1）柱面的形成 由直母线AA1沿着一曲导线A1B1C1A1，且平行于另一直导 线MN运动而形成的曲面。 （2）柱面的投影 画出直母线、曲导线以及外形 轮廓素线和其它必要的素线 （3）柱面的种类
柱面投影种类
纬圆、赤道圆与径圆
回转面按旋转运动的 特性，母线上任意一点 的旋转轨迹都是一个垂 直于轴线的圆，称为纬 圆，纬圆的半径等于该 点到轴线的距离。其中 比相邻两侧的纬圆都大 的，称为赤道圆；比相 邻两侧的纬圆都小的， 称为径圆或喉圆。

画法几何曲面体的投影及其表面取点

画法几何曲面体的投影及其表面取点

方法一：素线法 方法二：纬线圆法
位于特殊位置的 点直接确定
c' （a’）
b'
c" a"
（b”）
a
c b
三、圆球
1. 球面的形成—— 半圆绕其直径为轴旋转一周的轨迹
球面的三种形成方式
圆绕铅垂线旋转
圆绕正垂线旋转
圆绕侧垂线旋转
３、球体投影图的画法
注
意
三
O’
O’’
个
投
影
图
之
间
的
对
应
O
关
系
4、球体表面转向素线的投影位置
O’
O’’
O
1）对正投 影面的转 向素线
2）对侧投 影面的转 向素线
3）对水平 投影面的转 向素线
注意球体表 面的转向素线在 三个投影图中的 对应位置
例： 已知球面上的A、B、C 的一个投影，求其余投影。
a'
(b')
c'
a"
(b")
c"
b (c) a
四、圆环体的投影
１、圆环体的形成
圆环体是 由圆作为母线 围绕同平面内 的一根轴线旋 转一周而形成 的回转体。
注意 三个投影 图之间的 对应关系。
3. 圆柱表面取点——利用积聚性作图
a’
a’
a”
a”
A
a
a
二、圆锥
1. 圆锥面的形成—— 动直线绕与其相交的固定轴线旋转的轨迹
素线
母线
M
圆锥面上的素线和纬线圆
素线
纬圆
2. 圆锥的投影图画法
s'
s"

曲面立体投影及表面上求点(ppt 14页)

曲面立体投影及表面上求点(ppt 14页)
例3.4 已知点M属于圆锥表面，并知M点的正面投影m′，分别用辅助素线法和 辅助圆法求M点的其他两投影面的投影m，m″，如图3-12所示。
作图: ①用辅助素线法 根据m′的位置和可见性，可判定M点位于圆锥面，由于圆锥面的投影图没有 积聚性，利用辅助素线法，如图3-12（a）所示过锥顶S和点M作一条辅助素线SⅠ， 在图3.12（b）中连接s′m′，并延长到与底平面的正面投影相交于1′，求得s1 和s″1″;再根据点属于直线的判断依据，按长对正由m′求出m，按高平齐或宽相 等由m′或m求出m″。
图3-10 求属于பைடு நூலகம்柱表面的点的投影
作图: 由给定的m′的位置和可见性，可以判定M点位于左前四分之一圆柱面上，所以 求M点的投影作图过程是:首先利用圆柱面在H面的投影的积聚性，按长对正的投影 对应关系求出积聚于圆周的m，然后分别由m及m′，按高平齐、宽相等的投影对应 关系求出m″。求N点的投影作图过程读者可参考上例自行分析。其投影的可见性如 图3-10所示。
7.曲面立体投影及表面上求点
图3-13 圆球的结构特征及投影作图过程
7.曲面立体投影及表面上求点
例3.5 已知点M属于圆球表面，并知M点的水平投影m，求其他两投影面的投 影，如图3-13（e）所示。
作图: 根据m的位置和可见性，可以判定M点位于前半球左上部的表面，利用辅助圆 法，过M点在球表面做一平行于V面的辅助圆（也可以作平行于H面或W面的辅助 圆），则该辅助圆在水平投影的图形为过m点的平行于X轴的直线ef，其正面投影的 图形为直径等于 e′f′的圆，其侧面投影的图形为平行于Z轴的直线，则M点的其他 两面投影必属于该辅助圆的同面投影。最后根据M点的位置特点，判断M点的三个投 影都是可见的。
7.曲面立体投影及表面上求点

工程图学第5章立体的投影

工程图学第5章立体的投影

电子设备中的立体设计
1 2 3
电子设备的立体结构
电子设备的立体结构通常由电路板、外壳、连接 器等组成，这些组件通过不同的方式组装在一起。
电子设备的立体布局
电子设备的立体布局需要考虑设备的空间利用率、 散热性能、电磁屏蔽等因素，以确保设备能够正 常工作。
电子设备的立体配合
电子设备中的各个组件需要进行配合，以确保它 们能够正确地组装在一起，并实现预定的功能。
04
平面立体的投影
棱柱体的投影
棱柱体的投影
棱柱体由两个平行的多边形底面和若干个矩形侧面组成。在 投影图中，多边形的各顶点分别投影到与底面平行的投影面 上，各边中点连接得到棱柱体的投影。
棱柱体的三视图
棱柱体的三视图包括正视图、侧视图和俯视图。正视图显示 棱柱体的正面形状，侧视图显示侧面形状，俯视图显示顶面 形状。
THANKS
感谢观看
棱锥体的投影
棱锥体的投影
棱锥体由一个多边形底面和若干个三 角形侧面组成。在投影图中，多边形 的各顶点分别投影到与底面平行的投 影面上，各边中点连接得到棱锥体的 投影。
棱锥体的三视图
棱锥体的三视图包括正视图、侧视图 和俯视图。正视图显示棱锥体的正面 形状，侧视图显示侧面形状，俯视图 显示顶面形状。
圆柱体的投影
圆柱体的投影
圆柱体由一个圆底面和一个侧面组成。在投影图中，圆底面的圆心投影到与底面平行的投影面上，圆周上的点连 接得到圆柱体的投影。
圆柱体的三视图
圆柱体的三视图包括正视图、侧视图和俯视图。正视图显示圆柱体的正面形状，侧视图显示侧面形状，俯视图显 示顶面形状。
圆锥体的投影
圆锥体的投影
圆锥体由一个圆底面和一个侧面组成。在投影图中，圆底面的圆心投影到与底面平行的投影面上，圆 周上的点连接得到圆锥体的投影。

工程图学基础第3章 立体的投影

工程图学基础第3章 立体的投影

1.平面与棱锥相交
图3-14 平面与三棱锥相交
2.平面与棱柱相交
例3-10 画出截切五棱柱的三面投影(图3-15)。 解 五棱柱被正垂面P截切，所得截交线为五边形。正面投影积聚在PV上，截平面与 侧表面CC1B1B，BB1A1A，AA1E1E、EE1D1D的交线的水平投影积聚在各自侧表面的 水平投影上。截平面与顶面ABCDE均垂直于V面，则交线为一正垂线，正面投影积聚 为一点。水平投影反映实长。截交线的侧面投影可由正面投影和水平投影求出。作图 步骤如下(图31)画出五棱柱的投影。 2)根据题目给定条件画出截平面的正面迹线PV。 3)求出截交线的水平投影五边形gfjih和侧面投影五边形g″f″j″i″h″。 4)去掉截切部分多余的轮廓线AF、BG、EJ及顶面上五边形BAEIH的投影，并判别投 影图的可见性。
(1)圆柱
图3-4 圆柱的三面投影
(2)圆锥
3-5 圆锥的三面投影
(3)圆球
图3-6 圆球的三面投影
(4)圆环
图3-7 圆环的三面投影
2.曲面立体表面上的点、线
(1)圆柱表面上的点、线 当圆柱轴线垂直于某一投影面时，圆柱面对其投影有积聚 性，利用积聚性确定属于圆柱表面上的点。 (2)圆锥表面上的点、线 为了确定属于圆锥面上的点，根据圆锥面的性质可过圆锥 顶点作辅助直线，或者过给定点作辅助圆，如图3-10a所示。 (3)圆球表面上的点、线 由于圆球面上不存在直线。
(1)棱锥Байду номын сангаас投影
图3-1 三棱锥的投影
(2)棱柱的投影
图3-2 正五棱柱的投影
2.平面立体投影图的可见性判断
平面立体投影图的可见性判断实质上是判别立 体各棱线投影的可见性。通常采用分析立体表 面可见性的方法解决。判断立体表面可见性时， 应遵循的原则是：共一个棱线的两个表面对某 一投影面投影时，只要其中一个表面可见，则 该棱线的投影可见，如果两个投影均不可见， 则该棱线的投影不可见。

曲面立体表面点的投影

曲面立体表面点的投影

《机械制图》课程教案
《第三章立体表面交线的投影作图§3－1 立体表
面上点的投影》教案
授课教师：杨秋颖班级：机加14-1 时间：2014.9.4
课题：曲面立体的投影及表面取点
教学方法：讲授法
教学目的：1、讲解曲面立体的种类及其三视图画法
2、讲解在圆柱和圆锥体表面取点、取线的作图方法
目的要求：1、能够熟练掌握圆柱和圆锥体的三视图画法
2、能够熟练运用利用点所在的面的积聚性法和辅助线法在曲面立体表面取点、取线
教学重点：1、曲面立体的种类及其三视图画法。

2、在曲面立体表面取点、取线的作图方法
教学难点：在圆柱和圆锥体表面取点、取线的作图方法
【教学媒体和资源利用】多媒体课件
【教学过程设计】组织教学—引入—新授—小结—学生练习—作业
（a）立体图（b）投影图
同理可对侧面投影中三角形的两腰进行类似的分析。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

曲面立体表面点的投影 Document number：NOCG-YUNOO-BUYTT-UU986-1986UT
《机械制图》课程教案
《第三章立体表面交线的投影作图§3－1 立体表面上点的投影》教案
授课教师：杨秋颖班级：机加14-1 时间：课
题：曲面立体的投影及表面取点
教学方法：讲授法
教学目的：1、讲解曲面立体的种类及其三视图画法
2、讲解在圆柱和圆锥体表面取点、取线的作图方法
目的要求：1、能够熟练掌握圆柱和圆锥体的三视图画法
2、能够熟练运用利用点所在的面的积聚性法和辅助线法在曲面立体
表面取点、取线
教学重点：1、曲面立体的种类及其三视图画法。

2、在曲面立体表面取点、取线的作图方法
教学难点：在圆柱和圆锥体表面取点、取线的作图方法
【教学媒体和资源利用】多媒体课件
【教学过程设计】组织教学—引入—新授—小结—学生练习—作业
（a）立体图（b）投影图
图3－4 圆柱的投影及表面上的点
边画图边讲解作图方法与步骤。

总结圆柱的投影特征：当圆柱的轴线垂直某一个投影面时，
必有一个投影为圆形，另外两个投影为全等的矩形。

（2）圆柱面上点的投影
课件展示方法：利用点所在的面的积聚性法。

（因为圆柱的圆柱面和
两底面均至少有一个投影具有积聚性。

）
举例：如图3－4（b）所示，已知圆柱面上点M的正面投影
m′，求作点M的其余两个投影。

因为圆柱面的投影具有积聚性，圆柱面上点的侧面投影一定
重影在圆周上。

又因为m′可见，所以点M必在前半圆柱
面的上边，由m′求得m″，再由m′和m″求得m。

第二课时
（二）曲面立体的投影及表面取点
1、圆锥
圆锥表面由圆锥面和底面所围成。

如图3－5（a）所示，圆
锥面可看作是一条直母线SA围绕与它平行的轴线SO回转而
成。

在圆锥面上通过锥顶的任一直线称为圆锥面的素线。

（1）圆锥的投影
画圆锥面的投影时，也常使它的轴线垂直于某一投影面。

举例：如图3－5（b）所示圆锥的轴线是铅垂线，底面是水
平面，图3－5（c）是它的投影图。

圆锥的水平投影为一个
圆，反映底面的实形，同时也表示圆锥面的投影。

圆锥的正
面、侧面投影均为等腰三角形，其底边均为圆锥底面的积聚
投影。

正面投影中三角形的两腰s′a′、s′c′分别表示
圆锥面最左、最右轮廓素线SA、SC的投影，他们是圆锥面
正面投影可见与不可见的分界线。

SA、SC的水平投影sa、
sc和横向中心线重合，侧面投影s″a″（c″）与轴线重
合。

同理可对侧面投影中三角形的两腰进行类似的分析。

（b）立体图（c）投影
图
图3－5 圆锥的投影
边画图边讲解作图方法与步骤。

总结圆锥的投影特征：当圆锥的轴线垂直某一个投影面时，
则圆锥在该投影面上投影为与其底面全等的圆形，另外两个
投影为全等的等腰三角形。

（2）圆锥面上点的投影
方法：1）辅助线法。

2）辅助圆法。

举例：如图3－6、3－7所示，已知圆锥表面上M的正面投
课件展示
影m′，求作点M的其余两个投影。

因为m′可见，所以M
必在前半个圆锥面的左边，故可判定点M的另两面投影均为
可见。

作图方法有两种：
作法一：辅助线法如图3－6 （a）所示，过锥顶S和M
作一直线SA，与底面交于点A。

点M的各个投影必在此SA
的相应投影上。

在图3－6（b）中过m′作s′a′，然后
求出其水平投影sa。

由于点M属于直线SA，根据点在直线
上的从属性质可知m必在sa上，求出水平投影m，再根据
m、m′可求出m″。

（a）立体图（b）投影图
图3－6 用辅助线法在圆锥面上取点
边画图边讲解作图方法与步骤。

作法二：辅助圆法如图3－7（a）所示，过圆锥面上点M
作一垂直于圆锥轴线的辅助圆，点M的各个投影必在此辅助
圆的相应投影上。

在图3－7（b）中过m′作水平线a′
b′，此为辅助圆的正面投影积聚线。

辅助圆的水平投影为
一直径等于a′ b′的圆，圆心为s，由m′向下引垂线
与此圆相交，且根据点M的可见性，即可求出 m 。

然后再
由m′和m可求出m″。

课件展示
（a）立体图（b）投影图
图3－7 用辅助线法在圆锥面上取点
课件展示边画图边讲解作图方法与步骤。

3、圆球
圆球的表面是球面，如图3－8(a)所示，圆球面可看作是
一条圆母线绕通过其圆心的轴线回转而成。

（1）圆球的投影
如图3－8（b）所示为圆球的立体图、如图3－8（c）所示
为圆球的投影。

圆球在三个投影面上的投影都是直径相等的
圆，但这三个圆分别表示三个不同方向的圆球面轮廓素线的
投影。

正面投影的圆是平行于V面的圆素线A（它是前面可
见半球与后面不可见半球的分界线）的投影。

与此类似，侧
面投影的圆是平行于W面的圆素线C的投影；水平投影的圆
是平行于H面的圆素线B的投影。

这三条圆素线的其他两面
投影，都与相应圆的中心线重合，不应画出。

（b）立体图（c）投影图
图3－8 圆球的投影
边画图边讲解作图方法与步骤。

（2）圆球面上点的投影
方法：1）辅助圆法。

圆球面的投影没有积聚性，求作其表面上点的投影需采用辅助圆法，即过该点在球面上作一个平行于任一投影面的辅助圆。

举例：如图3－9(a)所示，已知球面上点M的水平投影，求作其余两个投影。

过点M作一平行于正面的辅助圆，它的水平投影为过m的直线ab，正面投影为直径等于ab长度的圆。

自m向上引垂线，在正面投影上与辅助圆相交于两点。

又由于m可见，故点M必在上半个圆周上，据此可确定位置偏上的点即为m′，再由m、m′可求出m″。

如图3－9（b）所示
（a）（b）图3－9 圆球面上点的投影
边画图边讲解作图方法与步骤。

四、小结
1、圆柱体的投影分析和投影特征。

2、圆锥体上表面求点的方法。

3、圆上表面求点方法
作业：
习题册P29（1）、（2）、(3)、（5）
版书设计
3-1立体表面上点的投影
一、棱柱圆柱表面上点的投影
1、圆柱举例
2、圆柱的投影规律
3、圆柱表面点的投影规律
二、圆锥表面上点的投影
1、圆锥的定义
2、圆锥的投影规律
3、圆锥表面上点的投影。