球的组合体(课前导学)学生

《8.1 基本几何图形》教案第2课时圆柱、圆锥、圆台、球、简单组合体【教材分析】立体几何是研究三维空间中物体的形状、大小、位置关系的一门数学学科，而三维空间是人们生存发展的现实空间，学习立体几何对我们更好地认识客观世界，更好地生存与发展具有重要意义。

在立体几何初步部分,学生将先从对空间几何体观察入手、认识空间图形；再以长方体为载体，直观认识和理解空间点、线、面的位置关系。

本节内容既是义务教育阶段“空间与图形”课程的延续和提高，也是后续研究空间点、线、面位置关系的基础，既巩固了前面所学的内容，又为后面内容的学习做了知识上和方法上的准备，在教材中起着承前启后的作用。

【教学目标与核心素养】课程目标1．认识圆柱、圆锥、圆台、球的结构特征．2．认识柱、锥、台、球及其简单组合体的结构特征，并能运用这些特征描述现实生活中简单物体的结构．数学学科素养1.数学抽象：简单组合体概念的理解；2.逻辑推理：圆柱、圆锥、圆台、球的结构特点；3.直观想象：判断空间几何体；4.数学运算：球的相关计算、最短距离等；5.数学建模：通过平面展开图将空间问题转化为平面问题解决，体现了转化的思想方法.【教学重点和难点】重点：掌握圆柱、圆锥、圆台、球的结构特征；难点：旋转体的相关计算.【教学过程】一、情景导入上节课学了常见的多面体：棱柱、棱锥、棱台，那么常见的旋转体有哪些？又有什么结构特点？要求：让学生自由发言，教师不做判断。

而是引导学生进一步观察.研探.二、预习课本，引入新课阅读课本101-104页，思考并完成以下问题1、旋转体包含哪些图形？2、圆柱、圆锥、圆台、球是怎样定义的？又有什么结构特点？3、什么是简单组合体，特点是什么？要求：学生独立完成，以小组为单位，组内可商量，最终选出代表回答问题。

三、新知探究一、常见的旋转体1、圆柱：定义：以矩形的一边所在的直线为旋转轴，其余三边旋转形成的面所围成的旋转体。

旋转轴叫做圆柱的轴；垂直于轴的边旋转而成的圆面叫做圆柱的底面；平行于轴的边旋转而成曲面叫做圆柱的侧面；无论旋转到什么位置，不垂直于轴的边都叫做圆柱侧面的母线。

A. 2 B. 3 C. 2 D. 3
2
2
【分析】精确拟定截面圆在原图中的位置. 【解析】由题意得知：截面过正四周体的两个顶点，
故 EC= 3 . EF为△BEC边BC上的高，
从而 EF EC2 FC2 2 . 于是 S 1 BC EF = 2，
2 故选 C.
10
例２ 如图，在斜三棱柱ABC-A1B1C1，∠A1AB=∠A1AC， AB=AC，A1A=A1B=a，侧面B1BCC1与底面ABC所成的二面角 为120°，E、F分别是棱B1C1、A1A的中点.
于是 ∠A1AH为A1A与底面ABC所成的角. 由于 ∠A1AB=∠A1AC，因此AG为∠BAC的平分线.
又AB=AC，则AG⊥BC，且G为BC的中点.
由三垂线定理得A1A⊥BC.
由于A1A∥B1B，且EG∥B1B, 因此EG⊥BC.
于是∠AGE为二面角A-BC-E的平面角，
即 ∠AGE=120°.
A1
C1
B1
P
G
13
(3) 连结A1C. 在△A1AC和△A1AB中， 由于 AC=AB,∠A1AC=∠A1AB,A1A=A1A， 则△A1AC≌△A1AB， 故A1C=A1B.
由已知得 A1A=A1B=A1C=a. 又由于A1H⊥平面ABC，因此H为△ABC的外心.
设所求球的球心为O，O∈A1H，
➢(2)经线、纬线是 解决与地理有关的 球的问题的基本概 念，要理解这些知 识，并能合理利用 经度与纬度来解题. 在解决球面距离问 题时，熟练掌握求 经过两点的"大圆上 的劣弧长"的方法；
➢( 3 ) 求 球 的 表 面 积 、 体积，求两点的球 面距离，组合体等 问题时，常常把球 中的问题转化为相 应的轴截面来处理， 有时还利用圆的有 关性质、正弦定理 和余弦定理来解决 球的问题.

高中数学球体组合问题教案
课时安排：1课时
教学目标：
1. 熟练掌握球体组合问题的解题方法；
2. 能够灵活运用组合数学知识解决现实生活中的问题；
3. 培养学生分析和解决问题的能力。

教学内容：
球体组合问题的解题方法
教学步骤：
1. 引入新知识（5分钟）
通过展示一道球体组合问题，引导学生思考如何解决这个问题。

2. 理解概念（15分钟）
解释组合数学中的球体组合问题是指在一组球体中选择出若干个球体的组合方式。

讲解组合数学的基本概念和公式。

3. 练习与讨论（20分钟）
让学生通过练习题目，掌握球体组合问题的解题方法，并引导他们讨论解题思路。

4. 实践运用（15分钟）
给学生提供一些现实生活中的球体组合问题，让他们运用所学知识解决问题。

5. 总结与拓展（5分钟）
总结本节课所学的知识，并拓展到其他类型的组合问题。

教学工具：
投影仪、黑板、练习题目
作业布置：
布置相关练习题目作为课后作业，加深对球体组合问题的理解。

教学反思：
在教学中要注重引导学生思考问题的方法和逻辑，培养他们的解决问题的能力，并且要和现实生活结合起来，让学生感受到数学知识的实际应用。

3
三角剖分
球面可以通过三角剖分法拆分成无数小三角形
球的面积计算公式
表面积定义
球体的表面积S指的是球面区域的大小，以平方单位表示
计算表面积公式
S = 4πr²
球的体积计算公式
体积定义
球体的体积V指的是球内区域的大小，以立方单 位表示
计算体积公式
V = (4/3)πr³
球的常见应用场景
1 宇宙
2 生物学
探索球的奥秘
球体是宇宙中最简单的三维几何体之一。本课件将为您揭开球体的神秘面纱， 探索其结构特征、计算公式以及常见应用场景。
球的定义及基本特征
定义
球体是由一个点向四周所画的一条线，经过 该点且长度相等的所有点组成的图形。
特征
• 球体由无数个面相接构成 • 球面上的所有点到球心的距离相等
球的几何形状
正二十面体Байду номын сангаас
球面被20个正等边三角形面所 覆盖，每个顶点都被恰好3个 三角形围绕
球的等积展开图
球的面展开平面图，每一面都 是同样的大小
实物球体
球的真实形状，可以是任何大 小或材质
球的结构特征
1
组成
球体由诸多的小球(离子，分子或原子)构成，通过电子而组成晶体
2
密度
整个球的密度在各点处相等，且密度相对其他几何体更高
行星、星球、恒星等天体几乎都是球形的
细胞、球菌等微生物前后靠接触，具有几 何均匀性
3 工业设计
4 竞技运动
球形镜头广泛应用于计算机视觉、无人机、 人工智能等领域
足球、篮球、乒乓球等一些球类运动以球 形物体为主要比赛工具
总结和要点
球体是一种几何结构简单、广泛应用的三维几何体，其密度均匀、形状规则、 计算公式简单。不仅是自然界、人类社会中广泛存在的一种几何形状，更是 工程计算、科学研究不可或缺的基础几何体。

高中数学必修2第1页 解密佛山吉红勇老师扣扣：一0七669八11高中数学必修2 1.1.1-1.1.2《柱、锥、台、球、简单组合体的结构特征》【知识要点】1、空间几何体的有关概念：空间几何体、多面体、旋转体2、棱柱的结构特征（重点）：1） 棱柱的有关概念 2）棱柱的分类 3）棱柱的记法 3、棱锥的结构特征（重点） 4、棱台的结构特征5、圆柱的结构特征（重点）6、圆锥的结构特征（难点）7、圆台的结构特征8、球的结构特征9、组合体的结构特征10、简单空间几何体的基本概念：(1)(2)特殊的四棱柱：【范例析考点】考点一．柱、锥、台、球的概念的理解 例1：一个棱柱是正四棱柱的条件是（ ）. A.底面是正方形，有两个侧面是矩形B.底面是正方形，有两个侧面垂直于底面C.底面是菱形，且有一个顶点处的三条棱两两垂直D.每个侧面都是全等矩形的四棱柱 【针对练习】1、下列说法中正确的是（ ）.A. 以直角三角形的一边为轴旋转所得的旋转体是圆锥B. 以直角梯形的一腰为轴旋转所得的旋转体是圆台C. 圆柱、圆锥、圆台的底面都是圆D. 圆锥侧面展开图为扇形，这个扇形所在圆的半径等于圆锥的底面圆的半径2、下列说法错误的是（ ）.A. 若棱柱的底面边长相等，则它的各个侧面的面积相等B. 九棱柱有9条侧棱，9个侧面，侧面为平行四边形C. 六角螺帽、三棱镜都是棱柱D. 三棱柱的侧面为三角形 3、下列说法中不正确的是（ ）.A 棱柱的侧面不可以是三角形B 有六个大小一样的正方形所组成的图形是正方体的展开图C 正方体的各条棱都相等D 棱柱的各条侧棱都相等 4、下列对棱柱说法正确的是（ ）A ．只有两个面互相平行 B.所有的棱都相等 C.所有的面都是平行四边形 D.两底面平行，且各侧棱也平行 5、棱台不具备的特点是（ ）A ．两底面相似 B. 侧面都是梯形C. 侧棱都相等D. 侧棱延长后交于一点6、有两个面互相平行, 其余各面都是梯形的多面体是（ ）A ．棱柱B ． 棱锥C ． 棱台D ．可能是棱台, 也可能不是棱台, 但一定不是棱柱或棱锥 7、构成多面体的面最少是（ ）A ．三个B ． 四个C ． 五个D ． 六个 8、下列说法正确的是（ ）.A. 平行于圆锥某一母线的截面是等腰三角形B. 平行于圆台某一母线的截面是等腰梯形C. 过圆锥顶点的截面是等腰三角形D. 过圆台上底面中心的截面是等腰梯形9、一个棱柱至少有 个面，面数最少的棱柱有 个顶点，有 条棱.10、棱柱的侧面是 形，长方体的侧面是 形，正方体的侧面是 形.考点二．柱、锥、台、球的简单运算 例2：如右图, 四面体P-ABC 中, PA=PB=PC=2,∠APB=∠BPC=∠APC=300. 一只蚂蚁从A点出发沿四面体的表面绕一周, 再回到A 点, 问蚂蚁经过的最短路程是_________． 【针对练习】1．边长为5cm 的正方形EFGH 是圆柱的轴截面, 则从E 点沿圆柱的侧面到相对顶点G 的最短距离是_______________． 2．已知三棱锥的底面是边长为a 的等边三角形，则过各侧棱中点的截面的面积为3．长方体的全面积为11，十二条棱的长度之和为24，则这个长方体的一条对角线长为4．一个圆台的母线长为12，两底面面积分别为4π和25π，求 （1）圆台的高： （2）截得此圆台的圆锥的母线长为 5． 一个圆锥的底面半径为2，高为6，在圆锥的内部有一个高为x 内接圆柱.（1）用x 表示圆柱的轴截面面积S ； （2）当x 为何值时，S 最大.考点三．有关截面问题例3：下列命题正确的是（ ）A ．平行与圆锥的一条母线的截面是等腰三角形B ．平行与圆台的一条母线的截面是等腰梯形C ．过圆锥母线及顶点的截面是等腰三角形D ．过圆台的一个底面中心的截面是等腰梯形【针对练习】1、用一个平面去截一个几何体，得到的截面是四边形，这个几何体可能是（）A．圆锥 B．圆柱 C．球体 D．以上都可能2、下列说法中正确的是（）A．半圆可以分割成若干个扇形B．面是八边形的棱柱共有8个面C．直角梯形绕它的一条腰旋转一周形成的几何体是圆台D．截面是圆的几何体，不是圆柱，就是圆锥3、甲：“用一个平面去截一个长方体, 截面一定是长方形”；乙：“有一个面是多边形,其余各面都是三角形的几何体是棱锥”.这两种说法（）A．甲正确乙不正确 B．甲不正确乙正确C．甲正确乙正确 D．不正确乙不正确4、用一个平面去截棱锥, 得到两个几何体, 下列说法正确的是（）A．一个几何体是棱锥, 另一个几何体是棱台B．一个几何体是棱锥, 另一个几何体不一定是棱台C．一个几何体不一定是棱锥, 另一个几何体是棱台D．一个几何体不一定是棱锥, 另一个几何体不一定是棱5、用一个平面去截正方体，所得的截面不可能是（）.A. 六边形B. 菱形C. 梯形D. 直角三角形6、用一个平面去截正方体，得到的截面可能是、、、、、边形。

使用CAD软件制作正方体与球的组合体的步骤包括建立三维模型、进行仿真分析、优化设计等。建立三维模型可以使用专业 的CAD软件，如SolidWorks、AutoCAD等。仿真分析可以使用有限元分析软件，优化设计可以通过调整参数来实现。
06
组合体的扩展思考
其他几何形状的组合
01
02
03
圆柱与圆锥的组合
形式美
运用对称、平衡、比例等美学原则， 可以赋予组合体和谐、优美的外观。
感谢观看
THANKS
几何形状的特性
对称性
正方体具有高度的对称性，其对称轴有六个，分别是经过相 对两面的中心的三条直线。
稳定性
由于正方体的结构特点，它是一种非常稳定的几何体，不易 发生形变。
空间位置关系
组合关系
正方体可以与其他几何体组合形成复杂的组合体。
运动关系
正方体可以在空间中做平移、旋转等运动。
02
球的基本特性
3D打印正方体与球的组合体的步骤包括设计模型、切片、打印和后处理等。设计软件可以使用专业的 CAD软件，如SolidWorks、AutoCAD等，也可以使用在线的3D模型设计平台。
手工制作
手工制作正方体与球的组合体需要一 定的手工技巧和材料。可以使用木材、 塑料、纸张等材料，通过切割、折叠、 粘合等步骤制作出组合体。
定义与性质
定义
球是三维空间中，所有与固定点等距的点的集合。
性质
球是中心对称和旋转对称的几何体，其表面是连续且光滑的。
几何形状的特性
1 2
体积
球的体积公式为 V = (4/3)πr³，其中 r 是球的半 径。
表面积
球的表面积公式为 A = 4πr², 其中 r 是球的间距离最短的点，即球心。

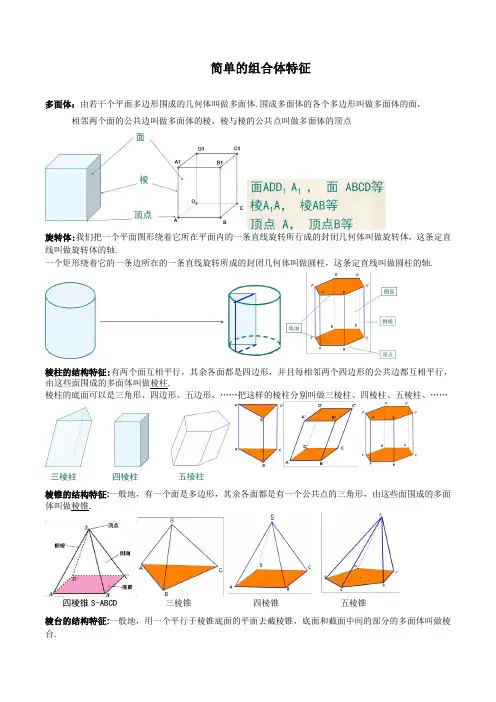
简单的组合体特征多面体：由若干个平面多边形围成的几何体叫做多面体.围成多面体的各个多边形叫做多面体的面，相邻两个面的公共边叫做多面体的棱，棱与棱的公共点叫做多面体的顶点旋转体:我们把一个平面图形绕着它所在平面内的一条直线旋转所行成的封闭几何体叫做旋转体，这条定直线叫做旋转体的轴.一个矩形绕着它的一条边所在的一条直线旋转所成的封闭几何体叫做圆柱，这条定直线叫做圆柱的轴.棱柱的结构特征:有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面围成的多面体叫做棱柱.棱柱的底面可以是三角形、四边形、五边形、……把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱、……棱锥的结构特征:一般地，有一个面是多边形，其余各面都是有一个公共点的三角形，由这些面围成的多面体叫做棱锥.四棱锥S-ABCD 三棱锥四棱锥五棱锥棱台的结构特征:一般地，用一个平行于棱锥底面的平面去截棱锥，底面和截面中间的部分的多面体叫做棱台.棱台的特点：两个底面是相似多边形,侧面都是梯形;侧棱延长后交于一点。

圆柱的结构特征:以矩形的一边所在直线为旋转轴，其余三边旋转形成的面所围成的旋转体叫做圆柱.旋转轴叫做圆柱的轴,无论旋转到什么位置不垂直于轴的边都叫做圆柱侧面的母线,平行于轴的边旋转而成的曲面叫做圆柱的侧面,垂直于轴的边旋转而成的面叫圆柱的底面.圆锥的结构特征:与圆柱一样，以直角三角形的一条直角边所在直线为旋转轴，其余两边旋转形成的面所围成的旋转体叫做圆锥.不垂直于轴的边旋转而成的曲面叫做圆锥的侧面,旋转轴叫做圆锥的轴,无论旋转到什么位置不垂直于轴的边都叫做圆锥侧面的母线,垂直于轴的边旋转而成的面叫圆锥的底面.圆台的结构特征:与棱台类似，用一个平行于圆锥底面的平面去截圆锥，底面和截面中间的部分的旋转体叫做棱台.球的结构特征:以半圆的直径所在直线为旋转轴，半圆面旋转一周形成的旋转体叫做球体，简称球.斜二测法：例１．用斜二测画法画水平放置的六边形的直观图()()()1ABCDEF AD x MN y ,oO O ,x Oy =4512O ,x A D =AD y M N =MN.N ,B C 2x ,BC;M ,E F x ,EF.3A B ,C D ,E F ,F 在六边形中，取 所在的直线为轴，对称轴所在直线为轴两轴交于点。

于轴的边旋转而成的曲面叫做
圆柱的侧面；无论旋转到什么位
置，平行于轴的边都叫做圆柱侧
面的母线
图形及表示
表示
圆柱用表示它 的轴的字母表 示，左图可表示 为__圆__柱__O_O__′ __
以__直__角__三__角__形__的__一__条__直__角__边___ 所在直线为旋转轴，其余两边旋 圆锥 转一周形成的面所围成的旋转 体叫做圆锥
(1)明确组合体的结构特征，主要弄清它是由哪些简单几何体组成的，必要时 也可以指出棱数、面数和顶点数．
(2)会识别较复杂的图形是学好立体几何的第一步，因此我们应注意观察周围 的物体，然后将它们“分拆”成几个简单的几何体，进而培养我们的空间想象能 力和识图能力．
[触类旁通] 2．如图为某竞赛中，获得第一名的代表队被授予的奖杯，试分析这个奖杯 是由哪些简单几何体组成的？
解析 奖杯由一个球，一个四棱柱和一个四棱台组成．
题型三 旋转体中的有关计算(一题多变) [例 3] 如图所示，用一个平行于圆锥 SO 底面的平面截这个圆锥，截得圆台 上、下底面的面积之比为 1∶16，截去的圆锥的母线长是 3 cm，求圆台 O′O 的 母线长．
[解析] 设圆台的母线长为 l，由截得圆台上、下底面面积之比为 1∶16，可 设截得圆台的上、下底面的半径分别为 r,4r.
过轴 SO 作截面，如图所示． 则△SO′A′∽△SOA，SA′＝3 cm. ∴SSAA′＝O′OAA′. ∴3＋3 l＝4rr＝41. 解得 l＝9(cm)， 即圆台的母线长为 9 cm.
[母题变式] 本例中若圆台的上底面半径为 1 cm，其他条件不变，试求圆台的高．
解析 ∵圆台的上底面半径为 1，故下底面半径为 4. 如图所示，在 Rt△A′HA 中 A′H＝ AA′2－AH2 ＝ 92－32＝6 2. 即圆台的高为 6 2 cm.

教学目标：1. 让学生掌握数学组合体的概念和性质。

2. 培养学生运用组合体知识解决实际问题的能力。

3. 培养学生的逻辑思维和空间想象能力。

教学重点：1. 数学组合体的概念和性质。

2. 组合体在生活中的应用。

教学难点：1. 组合体在空间中的形状变化。

2. 组合体在解决实际问题中的应用。

教学过程：一、导入1. 引导学生回顾平面几何中的基本图形，如三角形、四边形等。

2. 提出问题：在平面几何中，我们已经学习了这些基本图形，但在实际生活中，很多物体并不是简单的几何图形，而是由多个基本图形组合而成的。

今天我们就来学习数学中的组合体。

二、新课讲授1. 介绍数学组合体的概念：由多个基本图形组合而成的几何体称为数学组合体。

2. 讲解数学组合体的性质：组合体在空间中的形状变化、组合体的面积、体积计算等。

3. 通过实例讲解组合体在生活中的应用，如建筑、家具设计等。

三、课堂练习1. 让学生观察生活中常见的组合体，如椅子、桌子等，分析其组合方式。

2. 让学生动手拼搭简单的组合体，如正方体、长方体等，并计算其面积、体积。

3. 布置课后作业，让学生运用组合体知识解决实际问题。

四、课堂小结1. 回顾本节课所学内容，强调数学组合体的概念、性质和应用。

2. 引导学生思考组合体在生活中的重要作用。

五、课后作业1. 分析生活中常见的组合体，如汽车、飞机等，了解其组合方式。

2. 设计一个由多个基本图形组合而成的组合体，并计算其面积、体积。

3. 搜集组合体在生活中的应用案例，如建筑、家具设计等，撰写一篇小论文。

教学反思：本节课通过引入生活中的实例，让学生了解数学组合体的概念和性质，并培养了学生的空间想象能力和逻辑思维能力。

在今后的教学中，应进一步引导学生将所学知识应用于实际生活中，提高学生的综合素质。

同时，针对教学难点，可以适当增加课堂练习和课后作业，帮助学生巩固所学知识。

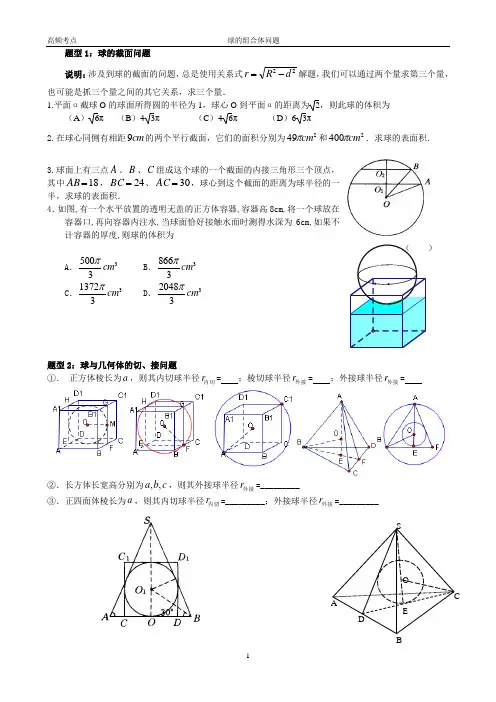
1题型1：球的截面问题说明：涉及到球的截面的问题，总是使用关系式22d R r -=解题，我们可以通过两个量求第三个量，也可能是抓三个量之间的其它关系，求三个量．1.平面α截球O 的球面所得圆的半径为1，球心O 到平面α的距离为2，则此球的体积为 （A ）6π （B ）43π （C ）46π （D ）63π2.在球心同侧有相距cm 9的两个平行截面，它们的面积分别为249cm π和2400cm π．求球的表面积．3.球面上有三点A 、B 、C 组成这个球的一个截面的内接三角形三个顶点，其中18=AB ，24=BC 、30=AC ，球心到这个截面的距离为球半径的一半，求球的表面积． 4．如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为）A ．35003cm π B ．38663cm πC ．313723cm πD ．320483cm π题型2：球与几何体的切、接问题①． 正方体棱长为a ，则其内切球半径r 内切= ；棱切球半径r 外接= ；外接球半径r 外接=②．长方体长宽高分别为c b a ,,，则其外接球半径r 外接=_________③．正四面体棱长为a ，则其内切球半径r 内切=_________；外接球半径r 外接=_________CBADSOE2④. 求球与它的外切圆柱、外切等边圆锥的体积之比．1.设长方体的长、宽、高分别为a a a ,,2,其顶点都在一个球面上，则该球的表面积为（A ）23a π （B ）26a π （C ）212a π （D ） 224a π练1.一个长方体的各顶点均在同一球的球面上，且一个顶点上的三条棱的长分别为1，2，3，则此球的表面积为 ．练2.，则其外接球的表面积是 .:练3．已知三棱柱111ABC A B C -的6个顶点都在球O 的球面上,34AB AC ==，,AB AC ⊥,112AA =,则球O 的半径为（ ）A．2 B．C ．132D．2．已知一个正方体的所有顶点在一个球面上. 若球的体积为92π, 则正方体的棱长为 ______. 3.过球O 表面上一点A 引三条长度相等的弦AB 、AC 、AD ，且两两夹角都为︒60，若球半径为R ，求弦AB 的长度．4. 正三棱锥的高为1，底面边长为62，正三棱锥内有一个球与其四个面相切．求球的表面积与体积．R ，以球心的位置特点来抓球的基本量，这是解决球有关问题常用的方法．5.已知三棱锥S ABC -的所有顶点都在球O 的球面上，ABC ∆是边长为1的正三角形，SC 为球O 的直径，且2SC =；则此棱锥的体积为（ ）()A 6 ()B6 ()C3 ()D 26．已知正四棱锥O-ABCD 的体积为,底面边长为,则以O 为球心,OA 为半径的球的表面积为________.7.已知矩形ABCD 的顶点都在半径为4的球O的球面上，且6,AB BC ==,则棱锥O ABCD-的体积为 。

教学过程
一、知识回顾：
1.多面体是由面和棱及顶点组成的．
2.旋转体可看作是由平面图形绕轴而成的．
3.棱柱、棱锥、棱台都是体；圆柱、圆锥、圆台、球都是体．
4.棱柱的侧棱互相，上下底面互相．圆柱的母线互相，圆台的母线．
5.棱台的上下底面且互相平行．
二、新知形成：
知识探究（一）：球的结构特征
球
图形及表示
定义：以所在直线为旋转轴，旋转一周所形成的旋转体叫做球体，简称球．
例2.试说明下列几何体分别是怎样组成的？
变式：
在正方体中按图中所示截去一个三棱锥，所剩部分有什么特征？
例3如图，四边形ABCD为平行四边形，EF∥AB，且EF<AB，试说明这个简单组合体的结构特征.
四、达标检测：
1．下列说法中不正确的 是
A棱柱的侧面不可以是三角形B有六个大小一样的正方形所组成的图形是正方体的展开图C正方体的各条棱都相等D棱柱的各条侧棱都相等
迁安一中数学组教案
授课时间
1
授课班级
编写人
审核人
教学内容
球和简单组合体的结构特征
教学目标
1.会用柱、锥、台、球的结构特征描述简单组合体的结构特征，理解柱与锥、锥与台的关系．
2．在描述简单组合体的结构特征过程中培养观察能力和空间想象能力．
教学重点
认识简单组合体的结构特征．
教学难点
由空间图形想象组合体的结构特征．
2、指出下图分别包含的几何体
（1）（2）（3）
课题
板书
设计
图中球可表示为
球心：半圆的叫做球的球心；
半径：半圆的叫做球的半径；
直径：半圆的叫做球的直径。
知识探究（二）：简单组合体的结构特征

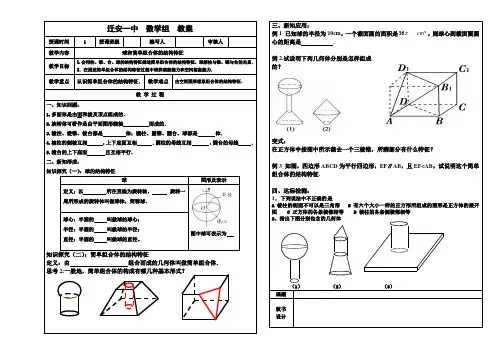
高一数学教学案材料编号:391.1.3.2球，组合体班级: 姓名：学号：设计人：李荣审查人:郭栋使用时间：12.5一．学习目标：1、掌握球的概念的形成过程及它的结构特征。

2、掌握球面距离的应用。

3、熟悉组合体的分解与合成。

二. 学习重点与难点：重点：球的结构特征。

难点：球面距离的概念及应用，组合体的分解与合成。

三．课前自学：（一）复习检测：已知下列三个命题：（1）在圆柱上，下底面圆周上各取一点，则这两点的连线是圆柱的母线；（2）圆锥顶点与底面圆周上任意一点的连线是圆锥的母线；（3）在圆台上，下底面圆周上各取一点，则这两点的连线是圆台的母线。

其中正确的命题个数为（）A．0 B.1 C.2 D.3（二）自学导学：1、思考：球具有哪些性质？哪些性质可以作为球集合的特征性质？2、知识点梳理：学点1、球的定义及性质:(1)定义:以半圆的所在的直线为旋转轴,半圆面旋转一周形成的几何体叫做简称.其中半圆的圆心叫做球的,如图中的.半圆的半径叫做.如图中的.半圆的直径叫做.如图中的.(2)球的记法：用表示球心的字母表示,如球O.(3)球的截面性质：①r=其中r为截面圆半径,,R为球的半径,d为球心O到截面圆的距离,即O到截面圆圆心'O的距离,如图所示.②球的大圆和小圆球面被经过球心的平面截得的圆叫做.被不经过球心的平面截得的圆叫做注：把地球看作一个球时,经线是球面上从北极到南极的半个大圆,赤道是一个大圆,其余的纬线都是小圆.学点2、球面性质：在球面上，两点之间的最短距离，就是经过两点的大圆在这两点间的一段劣弧的长度。

我们把这个弧长叫做两点的球面距离。

例如，飞机，轮船都尽可能地以大圆的圆弧（劣弧）为航线航行。

学点3、组合体:1.若干个简单的几何体经过适当的组合，可以得到一些比较复杂的几何体，这样的几何体叫做组合体。

常见的螺钉和螺母，螺钉可以看做是正六棱柱和圆柱的组合体。

螺母可以看做是正六棱柱中挖掉一个圆柱体。

以直角梯形的直角腰所在直线为旋转轴,其余三边旋转形成的面所围成 的旋转体叫做圆台.
上底面
侧面
母线
下底面
圆柱、圆锥、圆台的性质
1、底面都是圆 并且平行于底面的截面都是 圆
２、圆柱、圆锥、圆台过轴的截面（轴截面） 分别是矩形、等腰三角形、等腰梯形
7．球
如图8.1-13，半圆以它的直径所在直线为旋转轴，旋转一周形成的曲面叫做球 面，球面所围成的旋转体叫做球体（solid sphere），简称球．半圆的圆心叫 做球的球心；连接球心和球面上任意一点的线段叫做球的半径；连接球面上 两点并且经过球心的线段叫做球的直径．球常用表示球心的字母来表示，如 图8.1-13中的球记作球O．
（2）错误，反例如图
A
B
C
D
8.如图,长方体ABCD ABCD中被截去一部分,其中EH //AD.剩下的 几何体是什么? 截去的几何体是什么? 你能说出它们的名称吗?
剩下的几何体是棱柱，截去 的几何体也是棱柱；他们分 别是五棱柱和三棱柱。
D
H
C
A
E
B G
D
FC
A
B
9．如图，以平行四边形ABCD的一边AB所在直线为轴，其他三边旋转一周 形成的面围成一个几何体．画出这个几何体的图形，并说出其中的简单几何 体及有关的结构特征．
O 图8.1-13
半径 直径 球心
棱柱、棱锥、棱台、圆柱、圆锥、圆台和球是常见的简单几何体．其中棱柱 与圆柱统称为柱体，棱锥与圆锥统称为椎体，棱台和圆台统称为台体．
圆柱与棱柱统 称为柱体。
圆台与棱台统 称为台体。
圆锥与棱锥统 称为锥体。
探究 棱柱、棱锥与棱台都是多面体，它们在结构上有哪些相同点和不同点？当底 面发生变化时，它们能否互相转化？圆柱、圆锥与圆台呢？

球的组合体研究（球中的截面问题 及 球与其它几何体的切接问题）王宪良[学习目标]1.学习球与其它几何体切接的直观图的画法。

2.掌握球的截面的性质；3.理解掌握球的切接题目的类型和解法；4.培养空间想象能力，能根据题意正确画出组合体的直观图。

一、基础知识与概念： 1.有关定义（1）球：以半圆的直径所在直线为旋转轴，半圆面旋转一周形成的旋转体叫做球体，简称球.空间中到定点的距离等于定长的点的集合（轨迹）叫球面，（2）外接球：若一个多面体的各个顶点都在一个球的球面上， 则称这个多面体是这个球的内接多面体，这个球是这个多面体的外接球. 如图（3）内切球：若一个多面体的各面都与一个球的球面相切， 则称这个多面体是这个球的外切多面体，这个球是这个多面体的内切球.如图（4）大圆：过球心的平面截球面所得圆是大圆，大圆的半径与球的半径相等（它是截面圆中最大的圆）； （5）小圆：不过球心的截面所截得的圆叫小圆． 2．外接球的有关知识与方法 （1）性质：性质1：球的截面：用一个平面去截球，截面是圆面；用一个平面去截球面，截面是圆． 性质2：经过小圆的直径与且小圆面垂直的平面必过球心，该平面截球所得圆是大圆； 性质3：球心和截面圆心的连线垂直于截面（类比：圆的垂径定理）；性质4：在同一球中，过两不平行截面圆的圆心且垂直于相应的圆面的直线相交，交点是球心（类比：在同圆中，两相交弦的中垂线交点是圆心）；性质5：球心到截面的距离d 与球半径R 及截面圆半径r 的关系：222R d r =+． （2）结论：结论1：长方体的外接球的球心在体对角线的交点处，即长方体的体对角线的中点是球心；结论2：若由长方体截得的多面体的所有顶点是原长方体的顶点，则所得多面体与原长方体的外接球相同；结论3：长方体的外接球直径就是面对角线及与此面垂直的棱构成的直角三角形的外接圆圆心，换言之，就是：底面的一条对角线与一条高（棱）构成的直角三角形的外接圆是大圆；ca b初图2初图1NOO 1PEFOO 1D 1C 1B 1DCA 1O 2ABM结论4：圆柱体的外接球球心在上下两底面圆的圆心连线段中点处；结论5：圆柱体轴截面矩形的外接圆是大圆，该矩形的对角线（外接圆直径）是球的直径； 结论6：直棱柱与该棱柱的外接圆柱体有相同的外接球； 结论7：圆锥体的外接球球心在圆锥的高所在的直线上；结论8：圆锥体轴截面等腰三角形的外接圆是大圆，该三角形的外接圆直径是球的直径； 结论9：侧棱相等的棱锥与该棱锥的外接圆锥有相同的外接球.（3）终极利器：勾股定理、正弦定理及余弦定理（解三角形求线段长度）； 3．内切球的有关知识与方法（1）若球与平面相切，则切点与球心连线与切面垂直.（与直线切圆的结论有一致性）.（2）内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等(类比：与多边形的内切圆、外接圆) （3）正多面体的内切球和外接球的球心重合.（4）正棱锥的内切球和外接球球心都在高线上，但不一定重合. 4．基本方法：（1）构造三角形利用相似比和勾股定理；（2）体积分割是求内切球半径的通用做法（等体积法）. 二、理清位置，学会画图 先画一个大圆与一个或两个小圆。

第7页/共15页
思考3:试说明下列几何体分别是怎样组 成的？
第8页/共15页
思考4:一般地，简单组合体的构成有那
几种基本形式？
拼接，截割
思考5:试说明如图所示的几何体的结构 特征.
第9页/共15页
理论迁移
例1 如图，AB为圆弧BC所在圆的直 径，BAC 45 .将这个平面图形绕直线 AB旋转一周，得到一个组合体，试说明 这个组合体的结构特征.
A
D
C
B
第10页/共15页
例2 如图，四边形ABCD为平行四边形， EF∥AB，且EF<AB，试说明这个简单组合 体的结构特征.
E
F
E
F
D A
CD BA
第11页/共15页
C B
例3 如图，各棱长都相等的三棱锥
内接于一个球，则经过球心的一个截面 图形可能是 (1),(3) .
(1)
(2)
(3)
第12页/共15页
知识探究（一）：球的结构特征 思考1：现实生活中有哪些物体是球状几 何体？
NBA
第2页/共15页
思考2:从旋转的角度分析，球是由什么 图形绕哪条直线旋转而成的？
以半圆的直径所在直线为旋转轴，半圆 面旋转一周形成的旋转体叫做球体，简 称球.
第3页/共15页
思考3:半圆的圆心、半径、直径，在球 体中分别叫做球的球心、球的半径、球 的直径，球的外表面叫做球面.那么球的 半径还可怎样理解？
思考1:棱柱、棱锥、棱台都是多面体，但它 们有本质的区别.如果棱台上底面的大小发生 变化，它与棱柱、棱锥有什么关系？
思考2:现实世界中几何体的形状各种各样， 除了柱体、锥体、台体和球体等简单几何体 外，还有大量的几何体是由这些简单几何体 组合而成的，这些几何体叫做简单组合体.你 能说出周围物体所示的几何体是由哪些简单 几何体组合而成的吗？

常见几何体的外接球
(一)柱体的外接球 1.正方体 2.长方体 3.直棱柱（或圆柱）
1、正方体的内切球、外接球
2r a
2R
3a
2、长方体（或正四、六棱柱） 的外接球
体对角线=球直径
长方体中， a2 b2 c2 2R
3.直棱柱（或圆柱）的外接球
上下底面外接圆圆心连线的中点，即为球心
( A)
2 6
(B)
3 6
(C )
2 3
( D)
2 2
2． 【2012 辽宁理 16】已知正三棱锥 P ABC，点 P，A，B，C 都在半 径为 3 的求面上，若 PA，PB，PC 两两互相垂直，则球心到截 面 ABC 的距离为________。 3.（11 新课标理 15）已知矩形 ABCD 的顶点都在半径为 4 的球 O 的 球 面 上 ， 且 AB=6 ， BC=
点都在一个球面上，则该球的表面积为 (A) a
2
7 2 (B) 3 a
(C)
11 2 a 3
2 (D) 5 a
3. 直 三 棱 柱
A B C A1 B 1 C 1 的 各 个 顶 点 在 同 一 球 面 上 ， 若
AB AC AA1 2, BAC 120 ，则球的表面积为_______.
反思总结：
1.解决球的组合体问题的基本思路：找球心，求半径
正方体、长方体、直棱柱 2.锥体的外接球问题，可把锥体补成： 3.关于球的组合体的常见规律和结论，你能总结几个？
巩固强化：
1． 【2012 新课标 11】 已知三棱锥 S ABC 的所有顶点都在球 O 的求面上， ABC 是边长为1 的正三角形， SC 为球 O 的直径，且 SC 2 ；则此棱锥的 体积为（ ）

高中数学球体组合教案
一、教学目标：
1. 理解球体的基本概念；
2. 掌握球体的组合计算方法；
3. 能够应用球体组合问题解决实际问题。

二、教学内容：
1. 球体的体积和表面积；
2. 球体的排列组合；
3. 球体的应用问题。

三、教学重点：
1. 掌握球体的排列组合方法；
2. 熟练应用球体的相关知识解决实际问题。

四、教学过程：
一、导入：
教师出示几个不同大小的球体，并引导学生讨论球体的特点和性质。

二、讲授：
1. 球体的体积和表面积计算方法；
2. 球体的排列组合公式；
3. 球体组合问题的解决方法。

三、练习：
1. 练习球体的体积和表面积计算；
2. 练习球体的排列组合问题。

四、应用：
教师设计一些实际问题，让学生应用所学知识解决。

五、总结：
回顾本节课所学内容，并总结重点知识点。

六、作业：
布置相关练习作业，巩固所学知识。

五、教学环节设计：
1. 利用实物球体进行展示，激发学生的学习兴趣；
2. 融入实际问题，提高学生的问题解决能力；
3. 多种教学方法相结合，提高教学效果。

六、教学反馈：
及时收集学生学习情况，调整教学策略，提高教学效果。

七、教学评估：
对学生的学习情况进行定期评估，及时调整教学计划，确保教学效果。

以上就是本节课的教学内容，希望同学们能够认真学习，掌握球体的组合计算方法，提高数学能力。

祝大家学习进步！。