简单电阻电路分析-2理想电压源电流源的串并联和等效变换
- 格式:ppt
- 大小:810.00 KB
- 文档页数:2






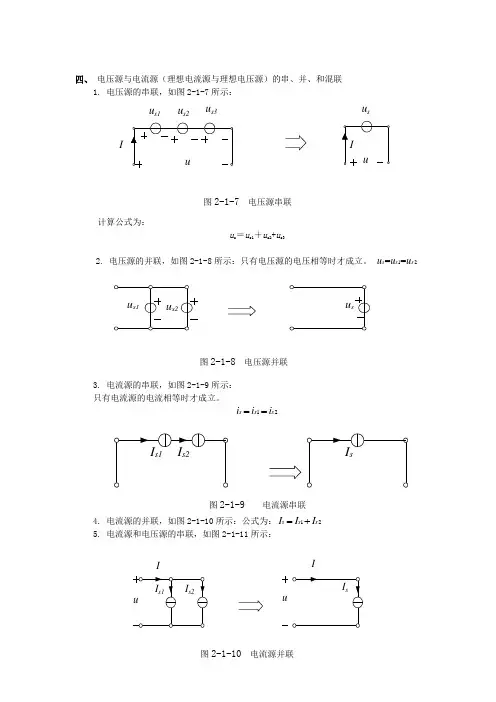
四、 电压源与电流源(理想电流源与理想电压源)的串、并、和混联1. 电压源的串联,如图2-1-7所示:计算公式为:u s =u s1+u s2+u s32. 电压源的并联,如图2-1-8所示:只有电压源的电压相等时才成立。
12==s s s u u u3. 电流源的串联,如图2-1-9所示: 只有电流源的电流相等时才成立。
12s s s i i i ==4. 电流源的并联,如图2-1-10所示:公式为:12s s s I I I =+5. 电流源和电压源的串联,如图2-1-11所示:u s1u s2us3u sI图2-1-7 电压源串联图2-1-8 电压源并联uII图2-1-10 电流源并联图2-1-9 电流源串联6. 电流源和电压源的并联,如图2-1-12所示:五、实际电源模型及相互转换我们曾经讨论过的电压源、电流源是理想的、实际上是不存在的。
那实际电源是什么样的呢?下面我门作具体讨论。
1. 实际电压源模型实际电压源与理想电压源的区别在于有无内阻R s 。
我们可以用一个理想电压源串一个内阻Rs 的形式来表示实际电压源模型。
如图2-1-13所示uu I s3Is3II图2-1-11 电流源和电压源串联uIII 图2-1-12 电流源和电压源的并联a bR s U U SabIU(a)实际电源 (b)实际电压源模型图2-1-13 实际电压源模型依照图中U 和I 的参考方向 得S S U U R I =- (2-1-5)由式(2-1-5)得到图2-1-13(c )实际电压源模型的伏安关系。
该模型用U S 和R s 两个参数来表征。
其中U S 为电源的开路U oc 。
从式(2-1-5)可知,电源的内阻R s 越小,实际电压源就越接近理想电压源,即U 越接近U S 。
2. 实际电流源模型实际电流源与理想电流源的差别也在于有无内阻R s ,我们也可以用一个理想电流源并一个内阻R s 的形式来表示实际的电流源,即实际电流源模型。

