计算电磁学-第八章-矩量法概述
- 格式:ppt
- 大小:897.50 KB
- 文档页数:36

计算电磁场的矩量法
计算电磁场的矩量法是一种通过求取电场和磁场的矩来计算电磁场行为的方法。
在矩量法中,电磁场被描述为一个有限数量的电荷和电流分布的集合。
这些分布被称为电荷和电流矩。
电荷矩是电荷分布的一种表示方式,它描述了电荷随其位置的变化而变化的程度。
电荷矩可以通过对电荷密度函数乘以相应的位置幂次项进行积分得到。
例如,一阶电荷矩可以通过对电荷密度函数乘以位置的一阶幂次项进行积分得到。
磁场矩是磁场分布的一种表示方式,它描述了磁场随其位置的变化而变化的程度。
磁场矩可以通过对磁场密度函数乘以相应的位置幂次项进行积分得到。
通过计算电荷和电流矩,可以得到电场和磁场的矩。
这些矩可以进一步用于计算电磁场的行为,例如电磁场的势能和辐射模式等。
矩量法在计算电磁场行为时具有一定的优点,例如可以处理复杂的几何形状和电磁场分布。
然而,在实际应用中,由于计算电荷和电流矩需要对电荷和电流分布进行积分,因此计算量较大。
此外,对于高阶电荷和电流矩,其计算误差可能会增加。
因此,在实际应用中需要综合考虑计算精度和计算效率等因素。

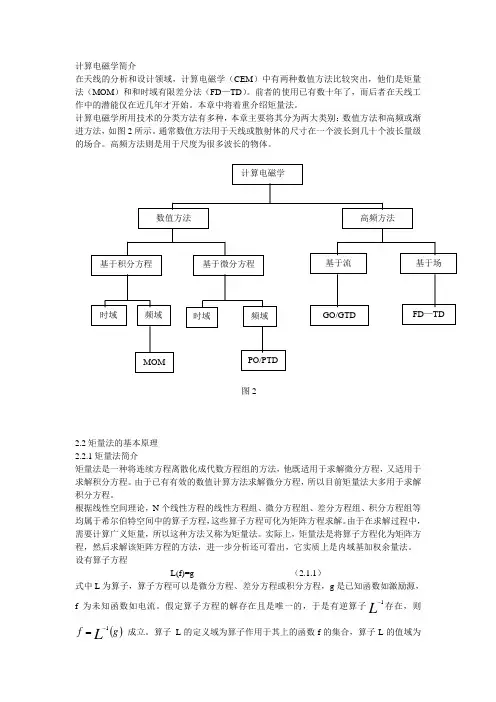
计算电磁学简介在天线的分析和设计领域,计算电磁学(CEM )中有两种数值方法比较突出,他们是矩量法(MOM )和和时域有限差分法(FD —TD )。
前者的使用已有数十年了,而后者在天线工作中的潜能仅在近几年才开始。
本章中将着重介绍矩量法。
计算电磁学所用技术的分类方法有多种,本章主要将其分为两大类别:数值方法和高频或渐进方法,如图2所示。
通常数值方法用于天线或散射体的尺寸在一个波长到几十个波长量级的场合。
高频方法则是用于尺度为很多波长的物体。
图22.2矩量法的基本原理 2.2.1矩量法简介矩量法是一种将连续方程离散化成代数方程组的方法,他既适用于求解微分方程,又适用于求解积分方程。
由于已有有效的数值计算方法求解微分方程,所以目前矩量法大多用于求解积分方程。
根据线性空间理论,N 个线性方程的线性方程组、微分方程组、差分方程组、积分方程组等均属于希尔伯特空间中的算子方程,这些算子方程可化为矩阵方程求解。
由于在求解过程中,需要计算广义矩量,所以这种方法又称为矩量法。
实际上,矩量法是将算子方程化为矩阵方程,然后求解该矩阵方程的方法,进一步分析还可看出,它实质上是内域基加权余量法。
设有算子方程L(f)=g (2.1.1)式中L 为算子,算子方程可以是微分方程、差分方程或积分方程,g 是已知函数如激励源,f 为未知函数如电流。
假定算子方程的解存在且是唯一的,于是有逆算子L1-存在,则()g f L 1-= 成立。
算子 L 的定义域为算子作用于其上的函数f 的集合,算子L 的值域为计算电磁学 数值方法 高频方法 基于积分方程 基于微分方程 时域 频域 时域 MOM FD —TD 基于场 基于流 GO/GTD PO/PTD 频域算子在其定义域上运算而得的函数g 的集合。
假定两个函数f1和f2以及两个任意常数a 1和a2有如下关系:()()()f a f a fa f a L L L 22112211+=+则称L 为线性算子。

矩量法在电磁散射中的应用一矩量法在电磁散射问题中的应用电磁散射问题是电磁学中的一个重要研究领域,研究电磁波的散射机理以及计算其散射场强的大小与分布,具有十分重要的实际意义。
矩量法作为一种有效的数值计算方法在其中有着广泛的应用。
但作为一种计算方法它也有着自己的缺陷,为了解决这些问题,人们提出了各种方案,矩量法在这个过程中也获得了很大的发展。
MoM(Method of Moments)原本是一种近似求解线性算子方程的方法,通过它可以将算子方程转化为一矩阵方程,进而通过求解此矩阵方程得到最终的近似解。
MoM最早是由两位数学家L. V. Kantorovich和V. I.Krylov提出的,后来由K.K.Mei引入计算电磁学,最终被R.F. Harryington在其著作《计算电磁场中的矩量法》中加以系统描述。
利用矩量法求解电磁问题的主要优点是:它严格地计算了各个子系统间的互耦,而算法本身又从根本上保证了误差系统总体最小而不产生数值色散。
如今MoM被广泛应用于计算电磁学中,虽然它不能处理电大尺寸目标的电磁问题,但基于MoM的各种加速方法仍受到极大重视,如多层快速多极子方法MLMFA等。
电磁散射问题是电磁学中的一个重要研究领域,研究电磁波的散射机理以及计算其散射场强的大小与分布,具有十分重要的实际意义。
在实际生活中,遇到的散射目标往往不仅具有复杂的几何形状,而且构成的材料也各不相同。
因此对复杂目标的电磁散射特性进行快速、高效的分析,具有重要的理论意义和实用价值。
电磁散射问题只有在相对简单的情况下才可以用严格的解析法来求解,比如对极少数形状规则的物体。
对于电大物体,可以用高频近似方法,例如几何光学法(GO)、物理光学法(PO)、几何绕射理论(GTD)、物理绕射理论(PTD)、一致性几何绕射理论(UTD)、复射线法(CT)等来求解散射场。
反之,对于电小物体,可以用准静态场来进行分析。
介乎这两者之间的物体,一般采用数值方法。

矩量法在电磁散射中的应用一矩量法在电磁散射问题中的应用电磁散射问题是电磁学中的一个重要研究领域,研究电磁波的散射机理以及计算其散射场强的大小与散布,拥有十分重要的本质意义。
矩量法作为一种有效的数值计算方法在此中有着宽泛的应用。
但作为一种计算方法它也有着自己的缺点,为认识决这些问题,人们提出了各样方案,矩量法在这个过程中也获取了很大的发展。
MoM(Method of Moments) 本来是一种近似求解线性算子方程的方法,经过它能够将算子方程转变为一矩阵方程,从而经过求解此矩阵方程获取最后的近似解。
MoM 最早是由两位数学家L. V. Kantorovich和 V. I.Krylov 提出的,后出处K.K.Mei 引入计算电磁学,最后被R.F. Harryington 在其著作《计算电磁场中的矩量法》中加以系统描绘。
利用矩量法求解电磁问题的主要长处是:它严格地计算了各个子系统间的互耦,而算法自己又从根本上保证了偏差系统整体最小而不产生数值色散。
现在 MoM 被宽泛应用于计算电磁学中,固然它不可以办理电大尺寸目标的电磁问题,但鉴于 MoM 的各样加快方法仍遇到极大重视,如多层快速多极子方法 MLMFA 等。
电磁散射问题是电磁学中的一个重要研究领域,研究电磁波的散射机理以及计算其散射场强的大小与散布,拥有十分重要的本质意义。
在本质生活中,碰到的散射目标常常不单拥有复杂的几何形状,并且组成的资料也各不同样。
所以对复杂目标的电磁散射特征进行快速、高效的剖析,拥有重要的理论意义和适用价值。
电磁散射问题只有在相对简单的状况下才能够用严格的分析法来求解,比方对很少量形状规则的物体。
关于电大物体,能够用高频近似方法,比如几何光学法 (GO)、物理光学法 (PO)、几何绕射理论 (GTD)、物理绕射理论 (PTD)、一致性几何绕射理论 (UTD)、复射线法 (CT)等来求解散射场。
反之,关于电小物体,能够用准静态场来进行剖析。

矩量法(Method of Moment)MoM, MM§1矩量法的基本原理1、内积两元素f和g的内积<f, g>是一个标量,性质:<f, g>=<g, f><(a1f+ a2g), h>= a1<f, h>+ a2<g, h> , a1,a2为标量<f, f*> >0 (0f); <f, f*> >0 (f=0) . f*为f的共轭2、算子方程L(f)=g, L~微分、差分、积分算子线性算子L :L(a 1 f 1+a 2f 2 )=a 1L(f 1)+a 2L(f 2), (a 1,a 2为常数) 若 <Lf, g>=<f, L a g>, 则称L a 为L 的伴随算子 若L a =L ,则L a 为自伴算子互易定理:若 源a :a m a J J ,→场a :a a H E ,;源b :b m b J J ,→场b :b b H E,; 则 <La, b>=dV J d H J d E bm a b V a )(1∙-∙⎰⎰⎰<a, L b>=dV J d H J d E amb a V b )(2∙-∙⎰⎰⎰ 若V1和V2重合,则<La, b>=<a, Lb> →互易定理(反应守恒)3、矩量法)()'((z g z f L = (1)g(z)为已知函数,为待求的未知函数(注意f, g 完全可能是矢量)∑==≈Nn n n n z f a z f 1)'()'( (2)n a 为待定系数(可以是复数),)'(z f n 为基函数(线性独立) 将(2)带入(1),交换L 与求和的次序(线性算子的性质))()]'([1z g z fL a N n n nn≈∑== (3)残数(残差):)()]'([)(1z g z f L a z N n n n n -=∑==ε 将上式两端与检验函数(权函数)求内积:><-><>=<∑==)(,)]'([,)(,1z g W z f L W a z W m Nn n n m n m ε (4)若令残数矢量对检验函数空间的投影为零,即:><)(,z W m ε=0 (5)即:0)(−−→−∞=N z ε由于误差正交于投影,所以它是二阶无穷小。



2 矩量法矩量法(method of moment )在电磁场分析中有着广泛的应用。
其概念相当简单,基本上是用未知场的积分方程去计算给定媒质中场的分布。
在静电学中,在由点()'','z y x 的电荷分布在点()z y x ,,产生的电位分布可以表示为()()⎰=''',','41,,v v Rdv z y x z y x V ρπε (2-1)这里()'','z y x v ρ实质上是电位分布的源,R 是点()z y x ,,和点()'','z y x 间的距离。
然而一般情况下()',','z y x v ρ是未知的,而源区电位的分布是给定的。
因此,为了求出空间每个地方的电位分布,我们必须估计源区的电荷分布()'','z y x v ρ。
设()'','z y x v ρ的一个解是()()()()()∑==+⋅⋅⋅++=ni i i n n v z y x z y x z y x z y x z y x 12211'',''',''',''',''','ραραραραρ(2-2)这里()'','z y x i ρ是源区一些离散位置上预先选定的电荷分布,i α是待定未知系数,以式(2-2)代入式(2-1)得()()⎰∑==='1''','41,,v ni iij j j j Rdv z y x z y x V V ραπε (2-3)()∑⎰==ni v jiii ij iR dv z y x V 1''','41ρπεα (2-4)这里n j ,,2,1⋅⋅⋅=。


一.细天线在天线的分析与设计中,矩量法应用非常广泛。
这里我们利用矩量法来分析细天线的辐射。
分析的思路是将矩量法应用于一个适当的叠加积分,就可以求解。
在R.F.Harrington 的1968年的著作《计算电磁场的矩量法》中,展示了一种利用滞后位积分来建立积分方程的方法,现在我们看看这种矩量法的模型是如何建立的。
1.1 积分方程的建立在外加场E ,的作用下,在导体上S 的电荷密度σ和电流密度J 的方程可用下述方法求得。
0E j A ωμ→→=−−∇Φ (1-1)4jkRSA Jds Reμπ−=∫∫(1-2)14jkRsds Re σεπ−Φ=∫∫ (1-3) J j σω−∇⋅= (1-4)根据边界条件,我们还可以得到:'n n E E ×=−× (1-5) R图1-1图1-1表示一根任意的细导线,我们作如下近似:(1)假定电流只是沿导线轴方向流动;(2)电流和电荷密度可以近似地认为是线电流I 及在导线轴上的σ。
(3)只对导线表面上E 的轴向分量使用边界条件式(1-5)。
近似后的公式为:'l l j E A lω∂Φ−=−−∂ (1-6) I(l)4jkRA dl Re μπ−=∫轴上 (1-7)1()4jkRldl R e σεπ−Φ=∫轴上(1-8) 1Ij lσω−∂=⋅∂ (1-9) 上式中l 是沿导线轴的长度变量,R 是从轴上源点指向导线表面的场点之间的距离。
图1-2上述方程的积分可以近似为沿N 个小段积分的总和,此时,在每个小段上将I 和q 视为常数。
图1-2表明将导线轴划分为N 个小段,第n 小段由始点n ,中点n 和终点n 组成,增量△ln 表明是在−+n −与n +之间,nl−Δ和nl+Δ分别表示增量沿l 上移动负的和正的二分之一增量。
所以(1-6)至(1-9)的积分变为:'()()()l l m m m j m E A l ω+−Φ−Φ−≈−−Δ (1-10) ()()4n jkRl n eA m I m dl R μπ−Δ≈∑∫ (1-11)1()()4n jkRnem n l dl R σεπ+−++ΔΦ≈∑∫ (1-12) 1(1)()()nI n I n j l σω++−+−≈⋅Δn (1-13) 由式(1-13)可以看出,各个σ可以用各个I 来表示。