Runge现象的研究

实验 七 塞曼效应实验英国物理学家法拉第(M ．Faraday)在1862年做了他最后的一个实验，即研究磁场对光源的影响的实验。

当时由于磁场不强，分光仪器的分辨率也不大，所以没有观测到在磁场作用下光源所发出的光的变化。

34年后，1896年荷兰物理学家塞曼(P ．Zeeman)在莱顿大学重做这个实验，他在电磁铁的磁极间将食盐(NaCl)放入火焰中燃烧发出的钠光，用3米凹面光栅(473条／毫米)摄谱仪去观察钠的两条黄线。

他发现在磁场的作用下，谱线变宽(如果磁场再强些或摄谱仪的分辨率再高些，就能看到谱线分裂)，这一现象称为塞曼效应。

当时原子结构的量子理论尚未产生，洛仑兹用经典的电子理论对这一现象进行了理论计算，得出所谓正常塞曼效应的结果，即当光源在外磁场的作用下，一条谱线将分裂成三条(垂直于磁场方向观察)和二条(平行于磁场方向观察)偏振化的分谱线。

当实验条件进一步改善以后，发现多数光谱线并不遵从正常塞曼效应的规律，而具有更为复杂的塞曼分裂。

这现象在以后的30年间一直困扰着物理学界，从而被称为反常塞曼效应。

1925年乌仑贝克和古兹米特为了解释反常塞曼效应和光谱线的双线结构，提出了电子自旋的假设。

应用这一假设能很好地解释反常塞曼效应。

也可以说：反常塞曼效应是电子自旋假设的有力根据之一。

普列斯顿(Preston)对塞曼效应实验的结果进行了深入研究，1898年发表了普列斯顿定则。

即同一类型的线系，具有相同的塞曼分裂。

龙格(Runge)和帕邢(Paschen)也进行了大量的实验研究，1907年发表了龙格定则。

即将所有塞曼分裂的图象，都可用正常塞曼效应所分裂的大小(做为一个洛仑兹单位)的有理分数来表示(见附注一)从他归纳钩结果中可以一目了然地看到所有塞曼分裂的图象和规律。

综上所述。

反常塞曼效应的研究推动了量子理论的发展和实验手段的进步，近年来在原子吸收光谱分析中用它来扣除背景，以提高分析的精度。

该实验证实了原子具有磁矩、自旋磁矩和空间量子化，迄今仍是研究原子能级结构的重要手段之一。

数值分析实验报告（02）一、实验目的通过上机绘制Runge 函数图像，理解高次插值的病态性质。

二、实验内容在区间[-1,1]上分别取n=10,n=20用两组等距节点对龙格(Runge)函数21()125f x x =+作多项式插值，对每个n 值分别画出()f x 和插值函数的图形。

三、编程思路（相关背景知识、算法步骤、流程图、伪代码）四、程序代码（Matlab 或C 语言的程序代码）function yt=Untitled8(x,y,xt)%UNTITLED5 ´Ë´¦ÏÔʾÓйش˺¯ÊýµÄÕªÒª% ´Ë´¦ÏÔʾÏêϸ˵Ã÷n=length(x);ny=length(y);if n~=nyerror('²åÖµ½ÚµãxÓ뺯ÊýÖµy²»Ò»ÖÂ');endm=length(xt);yt=zeros(1,m);for k=1:nlk=ones(1,m);for j=1:nif j~=klk=lk.*(xt-x(j))/(x(k)-x(j));endend ;yt=yt+y(k)*lk;endn=input('n=');x=linspace(-1,1,n);y=1./(1+25.*x.^2);xf=linspace(-1,1,100);yf=1./(1+25.*xf.^2)xl=xf;yl=Untitled8(x,y,xf);plot(xf,yf,'-b',xl,yl,'-r')五、数值结果及分析（数值运行结果及对结果的分析）当n=10时当n=20六、实验体会（计算中出现的问题，解决方法，实验体会）出现符号错误，代码函数变量不明重新输入，查询错误，找到并改正编码需要认真仔细，一定要头脑清晰，避免出现一些低级错误。

1 / 21数值分析实验二：插值法1 多项式插值的震荡现象1.1 问题描述考虑一个固定的区间上用插值逼近一个函数。

显然拉格朗日插值中使用的节点越多，插值多项式的次数就越高。

我们自然关心插值多项式的次数增加时， 是否也更加靠近被逼近的函数。

龙格（Runge ）给出一个例子是极著名并富有启发性的。

设区间[-1,1]上函数21()125f x x=+ (1)考虑区间[-1,1]的一个等距划分，分点为n i nix i ,,2,1,0,21 =+-= 则拉格朗日插值多项式为201()()125nn ii iL x l x x ==+∑(2)其中的(),0,1,2,,i l x i n =是n 次拉格朗日插值基函数。

实验要求：(1) 选择不断增大的分点数目n=2, 3 …. ，画出原函数f(x)及插值多项式函数()n L x 在[-1，1]上的图像，比较并分析实验结果。

(2) 选择其他的函数，例如定义在区间[-5，5]上的函数x x g xxx h arctan )(,1)(4=+=重复上述的实验看其结果如何。

(3) 区间[a,b]上切比雪夫点的定义为 (21)cos ,1,2,,1222(1)k b a b ak x k n n π⎛⎫+--=+=+ ⎪+⎝⎭(3)以121,,n x x x +为插值节点构造上述各函数的拉格朗日插值多项式，比较其结果,试分析2 / 21原因。

1.2 算法设计使用Matlab 函数进行实验, 在理解了插值法的基础上，根据拉格朗日插值多项式编写Matlab 脚本，其中把拉格朗日插值部分单独编写为f_lagrange.m 函数，方便调用。

1.3 实验结果1.3.1 f(x)在[-1,1]上的拉格朗日插值函数依次取n=2、3、4、5、6、7、10、15、20，画出原函数和拉格朗日插值函数的图像，如图1所示。

Matlab 脚本文件为Experiment2_1_1fx.m 。

可以看出，当n 较小时，拉格朗日多项式插值的函数图像随着次数n 的增加而更加接近于f(x)，即插值效果越来越好。

数值分析实验报告（四）题目：Runge现象的产生和克服学院：机电工程学院（二专业）专业：机械设计制造及其自动化班级：1008108班姓名：***学号：**********号Runge现象的产生和克服摘要：对于多项式插值运算，随着插值阶数的逐渐增多，如果带入离散点过于密集，使得定义域中的“边缘区域”，没有有效的点，将导致插值函数的边缘区域大幅度的偏离函数的真值，该现象称之为“Runge现象”。

0 前言（目的与意义）：了解Runge现象，体会插值运算的不准确性，以及其差值带来的误差甚至是错误。

1 数学背景：插值运算的误差公式：|w n (x)||R n (x)|<M n+1(n+1)!M n+1=max{f(n+1)(x i)}于是，如果函数的n+1阶导数一旦很大，则会出现函数的误差很大的情况。

2 程序及代码：（1）lagrange多项式插值函数syms f x p dp lx L;f=1/(1+25*x^2);N=input('请输入插值节点数N=');xx=-1:2/N:1;p=1; L=0;ff=zeros(1,length(xx));for i=1:(N+1)x=xx(i);ff(i)=eval(f);syms x;p=p*(x-xx(i));enddp=diff(p);for j=1:(N+1)x=xx(j);k=eval(dp);syms x;lx=p/((x-xx(j))*k);L=L+lx*ff(j);endaa=[-0.96:0.1:-0.06,0,0.06:0.1:0.96];for i=1:length(aa)x=aa(i);S(i)=eval(L);fff(i)=eval(f);ende=0;for i=1:length(aa)e=e+(S(i)-fff(i))^2;ende=sqrt(e/(20*21));fprintf('插值偏差为e=%.6f\n',e)ezplot(f,[-1,1])hold onezplot(L,[-1,1])hold onplot(xx,ff,'*')hold onplot(aa,S,'o')hold off（2）分段线性插值函数syms f x p lx;f=1/(1+25*x^2);N=input('请输入插值节点数N=');xx=-1:2/N:1;p=1; L=0;ff=zeros(1,length(xx));for i=1:(N+1)x=xx(i);ff(i)=eval(f);endsyms xfor i=1:Nfor j=1:(N+1)if j==ilx(i,j)=(x-xx(i+1))/(xx(i)-xx(i+1)); else if j==i+1lx(i,j)=(x-xx(i))/(xx(i+1)-xx(i)); elselx(i,j)=0;endendendendp=lx*ff';aa=[-0.96:0.1:-0.06,0,0.06:0.1:0.96];for i=1:length(aa)x=aa(i);for j=1:N+1if x<xx(j)breakendendS(i)=eval(p(j-1));fff(i)=eval(f);ende=0;for i=1:length(aa)e=e+(S(i)-fff(i))^2;ende=sqrt(e/(20*21));fprintf('插值偏差为e=%.6f\n',e)ezplot(f,[-1,1])hold onxxx=(-1:0.01:1);for i=1:length(xxx)x=xxx(i);for j=1:N+1if x<xx(j)breakendendSS(i)=eval(p(j-1));endplot(xxx,SS,'r')hold onplot(xx,ff,'*')hold onplot(aa,S,'o')hold off（3）：三转角插值法函数syms f x df s s1 s2 s3 s4;f=1/(1+25*x^2);df=diff(f);N=input('请输入插值节点数N=');h=2/N;xx=-1:2/N:1;p=1; L=0;ff=zeros(1,length(xx));for i=1:(N+1)x=xx(i);ff(i)=eval(f);dff(i)=eval(df);endsyms xfor i=1:Ns1=(x-xx(i+1))^2*(h+2*(x-xx(i)))*ff(i)/h^3; s2=(x-xx(i))^2*(h+2*(xx(i+1)-x))*ff(i+1)/h^3; s3=(x-xx(i+1))^2*(x-xx(i))*dff(i)/h^2;s4=(x-xx(i))^2*(x-xx(i+1))*dff(i+1)/h^2;s(i)=s1+s2+s3+s4;endaa=[-0.96:0.1:-0.06,0,0.06:0.1:0.96]; for i=1:length(aa)x=aa(i);for j=1:N+1if x<xx(j)breakendendS(i)=eval(s(j-1));fff(i)=eval(f);ende=0;for i=1:length(aa)e=e+(S(i)-fff(i))^2;ende=sqrt(e/(20*21));fprintf('插值偏差为e=%.6f\n',e) ezplot(f,[-1,1])hold onxxx=(-1:0.01:1);for i=1:length(xxx)x=xxx(i);for j=1:N+1if x<xx(j)breakendendSS(i)=eval(s(j-1));endplot(xxx,SS,'r')hold onplot(xx,ff,'*')hold onplot(aa,S,'o')hold off（4）.三弯矩插值法函数：syms f x ddf s;f=1/(1+25*x^2);ddf=diff(diff(f));N=input('请输入插值节点数N=');h=2/N;xx=-1:2/N:1;p=1; L=0;ff=zeros(1,length(xx));for i=1:(N+1)x=xx(i);ff(i)=eval(f);ddff(i)=eval(ddf);endsyms xfor i=1:NA=(ff(i+1)-ff(i))/h-h*(ddff(i+1)-ddff(i))/6;B=ff(i)-h^2*ddff(i)/6;s(i)=(xx(i+1)-x)^3*ddff(i)/(6*h)+(x-xx(i))^3*ddff(i+1)/(6*h)+A*(x-xx(i))+B; endaa=[-0.96:0.1:-0.06,0,0.06:0.1:0.96];for i=1:length(aa)x=aa(i);for j=1:N+1if x<xx(j)breakendendS(i)=eval(s(j-1));fff(i)=eval(f);ende=0;for i=1:length(aa)e=e+(S(i)-fff(i))^2;ende=sqrt(e/(20*21));fprintf('插值偏差为e=%.6f\n',e)ezplot(f,[-1,1])hold onxxx=(-1:0.01:1);for i=1:length(xxx)x=xxx(i);for j=1:N+1if x<xx(j)breakendendSS(i)=eval(s(j-1));endplot(xxx,SS,'r')hold onplot(xx,ff,'*')hold onplot(aa,S,'o')hold off3 总结与评价：函数的Runge现象可以通过三转角插值和三弯矩插值来解决，而且对于三转角和三弯矩插值来说，带入的数据越多，其插值效果越好4 实验结果：图1：观察Runge现象图2：分段线性插值图3：三转角插值：图4：三弯矩插值：。

《数值分析》实验报告实验序号：实验五 实验名称: 分段线性插值法1、 实验目的：随着插值节点的增加，插值多项式的插值多项式的次数也增加，而对于高次的插值容易带来剧烈的震荡，带来数值的不稳定（Runge 现象）。

为了既要增加插值的节点，减小插值的区间，以便更好的逼近插值函数，又要不增加插值多项式的次数以减少误差，可采用分段线性插值。

2、 实验内容：求一个函数ϕ(x )用来近似函数f (x )，用分段线性插值的方法来求解近似函数ϕ(x )并画出近似函数图像及原函数图像。

设在区间[a,b]上，给定n+1个插值节点b x x x x a n =<<<<=...210和相应的函数值n y y y ,...,,10，求一个插值函数)(x ϕ，满足以下条件：（1）),...,2,1,0()(n j y x j j ==ϕ; （2） )(x ϕ在每一个小区间[1,+j j x x ]上是线性函数。

对于给定函数11-,2511)(2≤≤+=x x x f 。

在区间[]11-，上画出f (x )和分段线性插值函数)(x ϕ的函数图像。

1. 分段线性插值的算法思想：分段线性插值需要在每个插值节点上构造分段线性插值基函数)(x l j ，然后再作它们的线性组合。

分段线性插值基函数的特点是在对应的插值节点上函数值取 1，其它节点上函数值取0。

插值基函数如下：⎪⎩⎪⎨⎧≤≤--=其它 ,0,)(101010x x x x x x x x l ⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≤<--≤≤--=+++---其它 ,0,,)(111111j j j j j j j j j j j x x x x x x x x x x x x x x x l⎪⎩⎪⎨⎧≤≤--=---其它 ,0,)(111n n n n n n x x x x x x x x l 设在节点a ≤x0<x1<…≤b=f(xi),(i=0,1,2,…,n)求折线函数L （x ）满足：（1） L(x)∈C[a,b]（2） L(x[i]=y[i])（3） L(x)在每个小区间（x[i],x[i+1]）上是线性插值函数￠（x ）叫做区间[a,b]上对数据（x[j],y[j]）(j=0,1,2,…,n)的分段区间函数。

实验报告一题目：非线性方程求解摘要：非线性方程的解析解通常很难给出，因此线性方程的数值解法就尤为重要。

本实验采用两种常见的求解方法二分法和Newton法及改进的Newton法。

前言：（目的和意义）掌握二分法与Newton法的基本原理和应用。

数学原理：对于一个非线性方程的数值解法很多。

在此介绍两种最常见的方法：二分法和Newton 法。

对于二分法，其数学实质就是说对于给定的待求解的方程f(x)，其在[a,b]上连续，f(a)f(b)<0，且f(x)在[a,b]内仅有一个实根x*，取区间中点c，若，则c恰为其根，否则根据f(a)f(c)<0是否成立判断根在区间[a,c]和[c,b]中的哪一个，从而得出新区间，仍称为[a,b]。

重复运行计算，直至满足精度为止。

这就是二分法的计算思想。

Newton法通常预先要给出一个猜测初值x0，然后根据其迭代公式产生逼近解x*的迭代数列{x k}，这就是Newton法的思想。

当x0接近x*时收敛很快，但是当x0选择不好时，可能会发散，因此初值的选取很重要。

另外，若将该迭代公式改进为其中r为要求的方程的根的重数，这就是改进的Newton法，当求解已知重数的方程的根时，在同种条件下其收敛速度要比Newton法快的多。

程序设计：本实验采用Matlab的M文件编写。

其中待求解的方程写成function的方式，如下function y=f(x);y=-x*x-sin(x);写成如上形式即可，下面给出主程序。

二分法源程序：clear%%%给定求解区间b=1.5;a=0;%%%误差R=1;k=0;%迭代次数初值while (R>5e-6) ;c=(a+b)/2;if f12(a)*f12(c)>0;a=c;elseb=c;endR=b-a;%求出误差k=k+1;endx=c%给出解Newton法及改进的Newton法源程序：clear%%%% 输入函数f=input('请输入需要求解函数>>','s')%%%求解f(x)的导数df=diff(f);%%%改进常数或重根数miu=2;%%%初始值x0x0=input('input initial value x0>>');k=0;%迭代次数max=100;%最大迭代次数R=eval(subs(f,'x0','x'));%求解f(x0)，以确定初值x0时否就是解while (abs(R)>1e-8)x1=x0-miu*eval(subs(f,'x0','x'))/eval(subs(df,'x0','x'));R=x1-x0;x0=x1;k=k+1;if (eval(subs(f,'x0','x'))<1e-10);breakendif k>max;%如果迭代次数大于给定值，认为迭代不收敛，重新输入初值ss=input('maybe result is error,choose a new x0,y/n?>>','s');if strcmp(ss,'y')x0=input('input initial value x0>>');k=0;elsebreakendendendk;%给出迭代次数x=x0；%给出解结果分析和讨论：1.用二分法计算方程在[1，2]内的根。

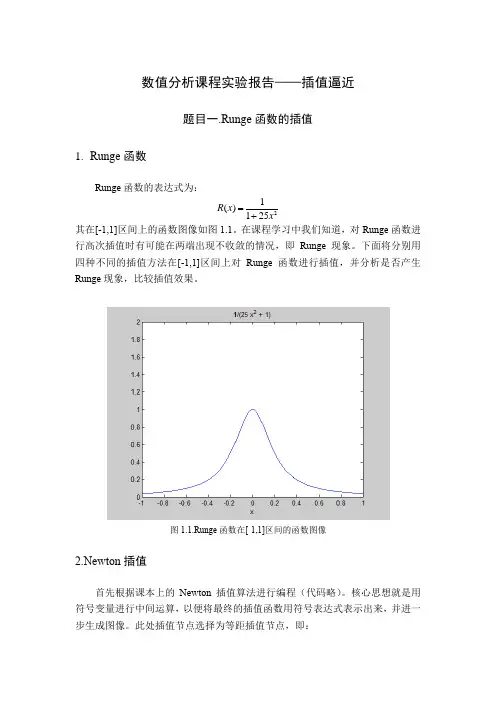
数值分析课程实验报告——插值逼近题目一.Runge 函数的插值1. Runge 函数Runge 函数的表达式为：21()125R x x =+ 其在[-1,1]区间上的函数图像如图1.1。

在课程学习中我们知道，对Runge 函数进行高次插值时有可能在两端出现不收敛的情况，即Runge 现象。

下面将分别用四种不同的插值方法在[-1,1]区间上对Runge 函数进行插值，并分析是否产生Runge 现象，比较插值效果。

图1.1.Runge 函数在[-1,1]区间的函数图像2.Newton 插值首先根据课本上的Newton 插值算法进行编程（代码略）。

核心思想就是用符号变量进行中间运算，以便将最终的插值函数用符号表达式表示出来，并进一步生成图像。

此处插值节点选择为等距插值节点，即：0.1(0,1,2,,)i x ih i =-+= (20)其中h=0.1。

插值曲线与原曲线的对比如图1.2（蓝色为原曲线，红色为插值曲线）。

从图中看出，在区间中部，二者吻合较好；但在区间两端二者则产生了明显偏差，甚至可以达到一个非常大的数值（e20量级）。

因此，在等距节点的20次Newton 插值下，产生了明显的Runge 现象。

图1.2.Newton 插值曲线与原曲线对比3. Lagrange 插值此处同样是根据Lagrange 插值的具体算法进行编程。

但插值节点不再是等距分布，而是如下形式：21cos()(0,1,2,,)42i i x i π+==…20 插值曲线与原曲线的对比如图1.3（蓝色为原曲线，红色为插值曲线）。

从图中看出，插值曲线与原曲线吻合的很好，没有产生明显的Runge 现象。

对比产生了明显Runge 现象的20次Newton 插值，Lagrange 插值的最高次数虽然也是20，但由于此处的插值节点不是等距分布的（事实上，此处采用的插值节点正是Chebyshev 多项式的零点），而是中间疏两边密，因此两侧较密的节点很好地抑制了Runge 现象。

山东师范大学数学科学学院实验报告x 0.1 0.5 1 1.5 2 2.5 3y 0.95 0.84 0.86 1.06 1.5 0.72 1.9y' 1 1.5 2 2.5 3 3.5 4求质点在时刻1.8时的速度，并画出插值多项式的图像。

1)运用Hermite插值法画出图像，如图4-1，并求质点在时刻1.8时的速度。

>>clear>>clc>>X=[0.1 0.5 1 1.5 2 2.5 3;0.95 0.84 0.86 1.06 1.5 0.72 1.9;1 1.5 2 2.5 3 3.5 4];>> x=0.1:0.01:3;>> H=Hermite1(X,x);>> plot(x,H)>> hold on>> plot(X(1,:),X(2,:),'r*')>> H1_8=Hermite(X,1.8);>> plot(1.8,H1_8,'go')>> legend('插值图像','原始点','目标点');图4-1二、验证高次插值的Runge现象问题分析和算法设计（一）Language插值代码function [Ln] =Lagrange(X,x)%请输入2*n+1矩阵X，X中第一行每个元素都是插值节点，X中第二行每个元素都是插值节点对应的函数值；%第二章P24例一拉格朗日插值n=size(X,2);d=0;for m=1:1:nif x==X(1,m);d=m;breakendend运行结果和总结 运行结果 例：给定函数55,11)(2≤≤-+=x xx f ； （1） 验证表2-10的误差结果（高次插值的Runge 现象）；（2） 以0.1为步长分别进行Language 插值、分段线性插值、分段三次Hermite插值，画出三种插值函数以及f(x)的图像，比较三种插值结果。

数值分析课程设计多项式插值的振荡现象远露冬201030770134指导教师李娇娇讲师学院名称理学院专业名称数学与应用数学提交日期2012年6月一、 问题的提出考虑在一个固定区间上用插值逼近一个函数。

显然，Lagrange 插值中使用的节点越多，插值多项式的次数就越高。

我们自然关心插值多项式增加时，Ln(x)是否也更加靠近被逼近的函数。

龙格(Runge)给出的一个例子是极著名并富有启发性的。

设区间[-1,1]上的函数：二、 实验内容考虑区间[-1,1]的一个等距划分，节点为则拉格朗日插值多项式为其中的a i(x),i=0,1,2,…,n 是n 次Lagrange 插值基函数。

1）选择不断增大的分点数n=2,3,4,5,6,7,8,9,101.画出原函数f(x)及插值多项式函数Ln(x)在[-1,1]上的图像；2.给出每一次逼近的最大误差；2）选择定义在区间[-5,5]上的函数重复上述实验看其结果如何。

3）区间[a,b]上切比雪夫(Chebychev)点的定义为以x1,x2,…,xn+1为插值节点构造上述各函数的Lagrange 插值多项式，比较其结果。

以下均用Matlab 软件绘制图象 (实线：f(x) 虚线：Ln(x))。

在这里为方便作比较，对于每个函数的不同的n 的取值都有上下两个函数图像比较，一组采用平均插值点，一组采用切比雪夫插值点， 并分别给出了两函数的误差最大值。

21()125f x x=+21,0,1,2,,i ix i nn=-+= 201()()125nn ii iL x a x x ==+∑(21)cos ,1,2,,1222(1)k b a b ak x k n n π⎛⎫+--=+=+ ⎪+⎝⎭对于函数： x ∈[-1,1]当n=2时平均插值点图像如下，此时max|f(x)- L2(x)|=0.6462-1-0.8-0.6-0.4-0.200.20.40.60.8100.20.40.60.81切比雪夫插值点图像如下，此时max|f(x)- L2(x)|=0.6006.-1-0.8-0.6-0.4-0.200.20.40.60.81-0.50.5121()125f x x =+当n=3时平均插值点图像如下，此时max|f(x)- L3(x)|=0.7070.-1-0.8-0.6-0.4-0.200.20.40.60.81切比雪夫插值点图像如下，此时max|f(x)- L3(x)|=0.7503.-1-0.8-0.6-0.4-0.20.20.40.60.8100.10.20.30.40.50.60.70.80.91当n=4时平均插值点图像如下：此时max|f(x)- L4(x)|= 0.4384-1-0.8-0.6-0.4-0.200.20.40.60.81-0.200.20.40.60.811.2切比雪夫插值点图像如下，此时max|f(x)- L4(x)|=0.4020.-1-0.8-0.6-0.4-0.200.20.40.60.81-0.200.20.40.60.811.2当n=5时平均插值点图像如下：此时max|f(x)- L5(x)|= 0.4327-1-0.8-0.6-0.4-0.200.20.40.60.81切比雪夫插值点图像如下，此时max|f(x)- L5(x)|=0.5559-1-0.8-0.6-0.4-0.20.20.40.60.8100.10.20.30.40.50.60.70.80.91n=6时平均插值点图像如下：此时max|f(x)-L6(x)|=0.6169-1-0.8-0.6-0.4-0.200.20.40.60.81-0.200.20.40.60.811.2切比雪夫插值点图像如下，此时max|f(x)- L6(x)|=0.2642-1-0.8-0.6-0.4-0.200.20.40.60.81-0.200.20.40.60.811.2-1-0.8-0.6-0.4-0.200.20.40.60.8100.20.40.60.81切比雪夫插值点图像如下，此时max|f(x)- L7(x)|=0.3917-1-0.8-0.6-0.4-0.20.20.40.60.8100.10.20.30.40.50.60.70.80.91-1-0.8-0.6-0.4-0.200.20.40.60.81切比雪夫插值点图像如下，此时max|f(x)- L8(x)|=0.1708-1-0.8-0.6-0.4-0.200.20.40.60.81-0.200.20.40.60.811.2-1-0.8-0.6-0.4-0.200.20.40.60.81-0.4-0.20.20.40.60.81切比雪夫插值点图像如下，此时max|f(x)- L9(x)|=0.2692-1-0.8-0.6-0.4-0.20.20.40.60.8100.10.20.30.40.50.60.70.80.91当n=10时平均插值点图像如下：此时max|f(x)- L10(x)|= 1.9157-1-0.8-0.6-0.4-0.200.20.40.60.81-0.500.511.52切比雪夫插值点图像如下，此时max|f(x)- L10(x)|=0.1092-1-0.8-0.6-0.4-0.200.20.40.60.81-0.200.20.40.60.811.2对于函数：()41h x xx +=x ∈[-5,5]当n=2时平均插值点图像如下, 此时max|f(x)- L2(x)|= 0.5687-5-4-3-2-1012345-0.8-0.6-0.4-0.200.20.40.6切比雪夫插值点图像如下，此时max|f(x)- L2(x)|= 0.5677.-5-4-3-2-1012345-0.8-0.6-0.4-0.20.20.40.6-5-4-3-2-1012345-0.8-0.6-0.4-0.20.20.40.6切比雪夫插值点图像如下，此时max|f(x)- L3(x)|= 0.5092.-5-4-3-2-1012345-0.8-0.6-0.4-0.20.20.40.6-5-4-3-2-1012345-0.8-0.6-0.4-0.20.20.40.6切比雪夫插值点图像如下，此时max|f(x)- L4(x)|= 0.5549.-5-4-3-2-1012345-0.8-0.6-0.4-0.20.20.40.6平均插值点图像如下, 此时max|f(x)- L5(x)|=0.6584.-5-4-3-2-1012345-0.8-0.6-0.4-0.200.20.40.60.8切比雪夫插值点图像如下，此时max|f(x)- L5(x)|= 0.3514.-5-4-3-2-1012345-0.8-0.6-0.4-0.20.20.40.6平均插值点图像如下, 此时max|f(x)- L6(x)|=0.4545.-5-4-3-2-1012345-0.8-0.6-0.4-0.20.20.40.6切比雪夫插值点图像如下，此时max|f(x)- L6(x)|= 0.5179.-5-4-3-2-1012345-0.8-0.6-0.4-0.20.20.40.6平均插值点图像如下, 此时max|f(x)- L7(x)|=1.4420.-5-4-3-2-1012345-1.5-1-0.50.511.5切比雪夫插值点图像如下，此时max|f(x)- L7(x)|= 0.3476.-5-4-3-2-1012345-0.8-0.6-0.4-0.20.20.40.6当n=8时平均插值点图像如下, 此时max|f(x)- L8(x)|=0.3247.-5-4-3-2-1012345-0.8-0.6-0.4-0.20.20.40.6切比雪夫插值点图像如下，此时max|f(x)- L8(x)|= 0.4463.-5-4-3-2-1012345-0.8-0.6-0.4-0.20.20.40.6平均插值点图像如下, 此时max|f(x)- L9(x)|=2.7365.-5-4-3-2-1012345-3-2-1123切比雪夫插值点图像如下，此时max|f(x)- L9(x)|= 0.3013.-5-4-3-2-1012345-0.8-0.6-0.4-0.200.20.40.60.8平均插值点图像如下, 此时max|f(x)- 10(x)|=0.8547.-5-4-3-2-112345-1-0.8-0.6-0.4-0.200.20.40.60.81切比雪夫插值点图像如下，此时max|f(x)- L10(x)|= 0.3431.-5-4-3-2-1012345-0.8-0.6-0.4-0.20.20.40.6对于函数：g(x)=arctanx , x ∈[-5,5]当n=2时平均插值点图像如下, 此时max|f(x)- L2(x)|= 0.5728-5-4-3-2-1012345-1.5-1-0.50.511.5切比雪夫插值点图像如下，此时max|f(x)- L2(x)|= 0.5173.-5-4-3-2-1012345-2-1.5-1-0.500.511.52当n=3，平均插值点图像如下, 此时max|f(x)- L3(x)|= 0.3593.-5-4-3-2-1012345-2-1.5-1-0.500.511.52切比雪夫插值点图像如下，此时max|f(x)- L3(x)|= 0.2325.-5-4-3-2-1012345-2-1.5-1-0.500.511.52-5-4-3-2-1012345-1.5-1-0.50.511.5切比雪夫插值点图像如下，此时max|f(x)- L4(x)|= 0.2887.-5-4-3-2-1012345-1.5-1-0.50.511.5-5-4-3-2-1012345-1.5-1-0.50.511.5切比雪夫插值点图像如下，此时max|f(x)- L5(x)|= 0.1378.-5-4-3-2-1012345-1.5-1-0.50.511.5-5-4-3-2-1012345-1.5-1-0.50.511.5切比雪夫插值点图像如下，此时max|f(x)- L6(x)|= 0.1700.-5-4-3-2-1012345-1.5-1-0.50.511.5-5-4-3-2-1012345-2-1.5-1-0.500.511.52切比雪夫插值点图像如下，此时max|f(x)- L7(x)|= 0.0822.-5-4-3-2-1012345-1.5-1-0.50.511.5当n=8时平均插值点图像如下, 此时max|f(x)- L8(x)|=0.1492.-5-4-3-2-1012345-2-1.5-1-0.500.511.52切比雪夫插值点图像如下，此时max|f(x)- L8(x)|=0.1022-5-4-3-2-1012345-1.5-1-0.50.511.5.当n=9时平均插值点图像如下, 此时max|f(x)- L9(x)|=0.5599.-5-4-3-2-1012345-1.5-1-0.50.511.5切比雪夫插值点图像如下，此时max|f(x)- L9(x)|= 0.0488.-5-4-3-2-1012345-1.5-1-0.50.511.5当n=10时平均插值点图像如下, 此时max|f(x)- 10(x)|=0.2026.-5-4-3-2-1012345-1.5-1-0.50.511.5切比雪夫插值点图像如下，此时max|f(x)- L10(x)|= 0.0622.-5-4-3-2-1012345-1.5-1-0.50.511.5三、 实验结果及分析为清晰明朗的观察随着n 的增加，每一次逼近的最大误差的变化，即max|f(x)- Ln(x)|的变化，这里以n 为代表横轴，max|f(x)- Ln(x)|代表纵轴，将其值在坐标上并用折线连接，实线表示平均插值点最大误差，虚线表示切比雪夫插值点最大误差，表示如下： 对于函数 x ∈[-1,1]234567891000.20.40.60.811.21.41.61.82对于函数()41h x xx +=x ∈[-5,5]0.511.522.5321()125f x x =+对于函数： g(x)=arctanx x ∈[-5,5]234567891000.10.20.30.40.50.60.7由以上实验内容，和所得的图像和数据可以得出以下结论：1.随着插值点n 的增大，采用平均插值点所得的拉格朗日逼近函数，在x 的中点位置附近（该三个例子中即x=0），与原函数越来越接近；在x 的两个端点位置，误差呈波动性逐渐增大；而采用切比雪夫插值点所得的拉格朗日逼近函数随着n 的增大，与原函数在x 的任何位置都越来越接近。

数值计算方法上机题目11、实验1. 病态问题实验目的：算法有“优”与“劣”之分，问题也有“好”和“坏”之别。

所谓坏问题就是问题本身的解对数据变化的比较敏感，反之属于好问题。

希望读者通过本实验对此有一个初步的体会。

数值分析的大部分研究课题中，如线性代数方程组、矩阵特征值问题、非线性方程及方程组等都存在病态的问题。

病态问题要通过研究和构造特殊的算法来解决，当然一般要付出一些代价（如耗用更多的机器时间、占用更多的存储空间等）。

问题提出：考虑一个高次的代数多项式∏=-=---=201)()20)...(2)(1()(k k x x x x x p （E1-1）显然该多项式的全部根为l ，2，…，20，共计20个，且每个根都是单重的（也称为简单的）。

现考虑该多项式方程的一个扰动0)(19=+xx p ε (E1-2)其中ε是一个非常小的数。

这相当于是对（E1-1）中19x 的系数作一个小的扰动。

我们希望比较（E1-1）和（E1-2）根的差别，从而分析方程（E1-1）的解对扰动的敏感性。

实验内容：为了实现方便，我们先介绍两个 Matlab 函数：“roots ”和“poly ”，输入函数u ＝roots （a ）其中若变量a 存储1+n 维的向量，则该函数的输出u 为一个n 维的向量。

设a 的元素依次为121,...,,+n a a a ，则输出u 的各分量是多项式方程0...1121=++++-n n n n a x a x a x a的全部根，而函数b=poly(v)的输出b 是一个n ＋1维变量，它是以n 维变量v 的各分量为根的多项式的系数。

可见“roots ”和“Poly ”是两个互逆的运算函数.ve=zeros(1,21); ve(2)=ess;roots(poly(1:20))+ve)上述简单的Matlab 程序便得到（E1-2）的全部根，程序中的“ess ”即是（E1-2）中的ε。

实验要求：（1）选择充分小的ess ，反复进行上述实验，记录结果的变化并分析它们。

题目1：对Runge 函数R(x ) =1在区间[-1,1]作下列插值逼近，并和1 + 25x 2R(x)的图像进行比较，并对结果进行分析。

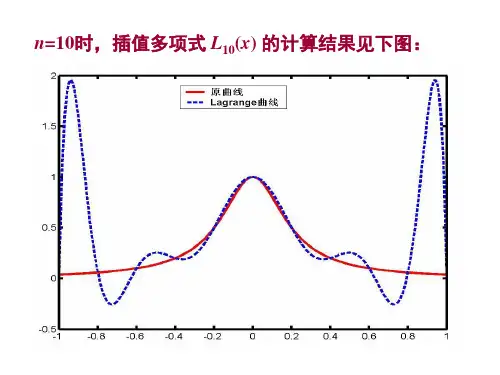
= -1 + ih,h= 0.1,0 ≤ i≤ 20 绘出它的20 次Newton 插值(1)用等距节点xi多项式的图像。

分别画出在[-1，1]区间，[-0.7，0.7]区间和[-0.5，0.5]区间上的 Newton 插值多项式和Runge 函数的图像从图中可以看出： 1）在[-0.5，0.5]区间 Newton 插值多项式和 Runge 函数的图像偏差较小，这说 明 Newton 插值多项式在此区间上可以较好的逼近 Runge 函数； 2）在边界（自变量 x=-1 和 x=1）附近，Newton 插值多项式和 Runge 函数的图像 偏差很大，Newton 插值多项式出现了剧烈的震荡。

（Runge 现象） (2)用节点 x = cos(2i + 1π）（, i = 0，1,2，⋅ ⋅ ⋅ ，20），绘出它的 20 次 Lagrangei 42 插值多项式的图像。

画出在[-1，1]区间上的 Lagrange 插值多项式和 Runge 函数的图像从图中可以看出：使用 Chebyshev 多项式零点构造的 Lagrange 插值多项式和 Runge 函数的图 像偏差较小，没有出现 Runge 现象。

(3)用等距节点 x i 的图像。

= -1 + ih ,h = 0.1,0 ≤ i ≤ 20 绘出它的分段线性插值函数画出在[-1，1]区间上分段线性插值函数和 Runge 函数的图像从图中可以看出：使用分段线性插值函数和 Runge 函数的图像偏差较小，也没有出现 Runge 现象，只在自变量 x=0 处有稍许偏差。

(4)用等距节点 x i 函数的图像。

= -1 + ih ,h = 0.1,0 ≤ i ≤ 20 绘出它的三次自然样条插值画出在[-1，1]区间上三次自然样条插值函数和 Runge 函数的图像从图中可以看出：使用三次自然样条插值函数和 Runge 函数的图像偏差较小，也没有出现 Runge 现象。