趣味数学078：至少两个人生日相同的概率有多大

两个人诞辰同样概率两个人诞辰同样的概率好多同学都有这样的体验，一个60 人左右的班级，问起大家诞辰的时候，常常会有那么几对同学的诞辰是同一天。

那么，这样“有缘”的事件发生的概率是多大呢？依据一般的思虑方式，一年有365 天，假如有多于365 人，那么依据我们熟习的抽屉原理，这些人中间必定会有起码两人诞辰同样。

假如只有 300 人，那么就不敢保证必定有诞辰同样的状况。

50 人的时候，这个概率会更小，依据我在四周人中间的检查，大多数人都以为这个概率小于百分之十。

可是实质情况是， 50 人的时候就极有可能有两人诞辰同样。

下边有一个小故事，又一次，美国数学家伯格米尼去观看世界杯足球赛，在看台上任意精选了22 名观众，让他们报出自己的诞辰，令现场球迷惊讶的是，居然有两个人的诞辰是同样的。

为了研究这个问题，能够采纳模拟实验的方式。

准备 365 张写有 1 至 365 的卡片，每次随机抽取一张，记下卡片上的数字，而后把卡片放回，而后重复上述步骤，直至抽取 50 张为止，而后比较所记下的数字。

经过大批的模拟实验，能够发现这个问题的概率是很大的。

计算此概率的公式以下：n:人数， P：起码两人诞辰同样的概率其实质计算结果是这样的，下边是一张概率表。

依据上表，结果是令人吃惊的， 50 人的时候，诞辰同样的概率高达 97.04%；假如人数许多于 23 人，这类可能性就会达到 50%。

这个问题的出乎意外之处在于其结果违犯了人们的直觉，其实，近似于这个问题的概率悖论还有好多，计算的结果常常和人们的预期相差甚远。

有的时候，我们一定依赖科学的计算方法来研究问题，而不是单凭推断。

1 / 1。

生日悖论：你的生日和其他人的生日有多大的概率相同？生日悖论是一个有趣的概率问题，它的答案可能会让你感到惊讶。

假设在一个房间里有23个人，那么这些人中有两个人生日相同的概率是多少呢？你可能会认为这个概率很小，但实际上它是非常高的。

为什么会这样呢？让我们来看看这个问题的背后。

生日悖论的原理在一个房间里有23个人，每个人的生日都是随机选择的。

那么第一个人的生日可以是任何一天，第二个人的生日可以是除了第一个人生日那一天的任何一天，第三个人的生日可以是除了前两个人生日那两天的任何一天，以此类推。

因此，第23个人的生日可以是除了前22个人生日那22天的任何一天。

我们可以用排列组合的方法来计算这个问题的答案。

假设我们要从365天中选择23个不同的生日，那么我们可以有C(365,23)种不同的选择方式。

其中C(n,m)表示从n个不同的物品中选择m个物品的组合数。

这个数值可以通过数学公式计算得出，也可以使用计算器或者网络上的计算工具来计算。

现在我们来计算一下，如果要保证在一个房间里至少有两个人的生日相同，需要多少人才能满足这个条件。

这个问题可以转化为求解至少有两个人的生日不同的概率，即：P = 1 - C(365,23) / 365^23这个概率的计算结果是0.5073，也就是说，在一个房间里有23个人的时候，至少有两个人的生日相同的概率是50.73%。

这个结果可能会让你感到惊讶，因为我们通常认为需要更多的人才能满足这个条件。

生日悖论的实际应用生日悖论不仅仅是一个有趣的概率问题，它还有着广泛的实际应用。

例如，在计算机科学和密码学中，生日悖论被用来评估哈希函数的强度。

哈希函数是一种将任意长度的消息映射到固定长度的消息摘要的算法，它在计算机安全中扮演着重要的角色。

生日悖论告诉我们，如果哈希函数的输出长度为n位，那么攻击者找到两个具有相同哈希值的消息的概率大约是2^(n/2)。

因此，为了保证哈希函数的安全性，输出长度应该足够长，以确保攻击者无法轻易地找到相同的哈希值。

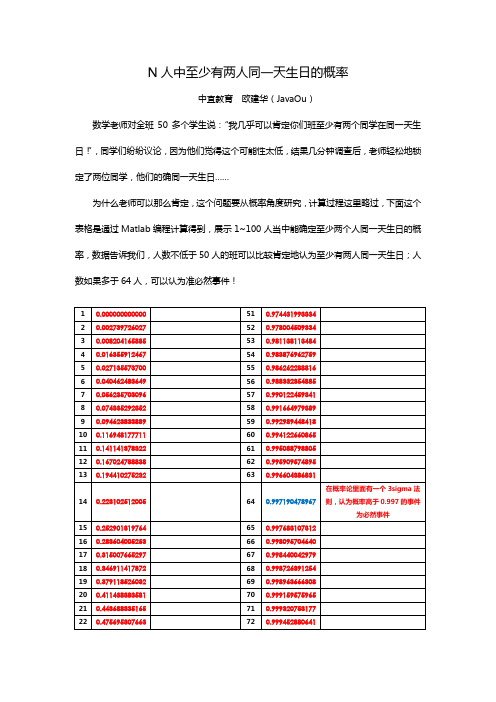
N人中至少有两人同一天生日的概率
中宜教育欧建华（JavaOu）
数学老师对全班50多个学生说：“我几乎可以肯定你们班至少有两个同学在同一天生日！”，同学们纷纷议论，因为他们觉得这个可能性太低，结果几分钟调查后，老师轻松地锁定了两位同学，他们的确同一天生日……
为什么老师可以那么肯定，这个问题要从概率角度研究，计算过程这里略过，下面这个表格是通过Matlab编程计算得到，展示1~100人当中能确定至少两个人同一天生日的概率，数据告诉我们，人数不低于50人的班可以比较肯定地认为至少有两人同一天生日；人数如果多于64人，可以认为准必然事件！。

生日概率的准确计算在我们的日常生活中，生日是一个非常重要的日子。

无论是家庭聚会、朋友聚会还是公司庆祝，生日都是一个值得庆祝的特殊时刻。

然而，你有没有想过在一群人中，生日相同的概率有多大呢？本文将介绍如何准确计算生日概率，以及一些有趣的生日统计数据。

我们来看一下生日概率的计算方法。

假设有n个人，我们想知道至少有两人生日相同的概率。

为了简化计算，我们可以先计算没有两人生日相同的概率，然后用1减去这个概率就是我们所要求的。

假设第一个人的生日是任意一天，那么第二个人的生日就不能和第一个人相同，有365种选择。

同理，第三个人的生日不能和前两个人相同，有364种选择。

以此类推，第n个人的生日不能和前n-1个人相同，有(365-(n-1))种选择。

所以，没有两人生日相同的概率为：P(n) = (365/365) * (364/365) * (363/365) * ... * (365-(n-1))/365接下来，我们可以使用这个公式计算不同人数下的生日概率。

下面是一些有趣的数据：1. 当有23个人时，至少有两人生日相同的概率超过一半，为50.73%。

这个结果可能有些出人意料，因为23个人实际上并不多。

2. 当有70个人时，至少有两人生日相同的概率超过99%，为99.41%。

这个结果也很有趣，因为70个人看起来也不算很多。

3. 当有365个人时，即每天都有一个人生日，必定会有至少两人生日相同。

这是因为365个人中的每个人都只有365种选择，所以生日相同的概率为100%。

通过这些数据，我们可以看出生日概率与人数之间的关系。

随着人数的增加，生日相同的概率也会增加。

这是因为随着人数的增加，生日的选择范围减小，导致生日相同的可能性增加。

除了计算生日概率，我们还可以通过生日统计数据来了解更多有趣的信息。

例如，美国的生日分布显示，9月份是全年中最多人出生的月份，而2月份是最少人出生的月份。

这可能与9个月前的圣诞节和新年的庆祝活动有关。

趣味统计学经典案例1. 生日悖论生日悖论是指在一个房间里，只需要23个人，就有50%以上的概率至少有两个人生日相同。

这个案例经典的体现了概率论中的鸽巢原理和生日悖论的概率计算。

2. 蒙提霍尔问题蒙提霍尔问题是指一个选手会面对三扇门，其中一扇门后面有奖品，另外两扇门后面是空的。

选手先选择一扇门，然后主持人会打开剩下两扇门中的一扇门，露出一扇空门。

选手是否应该换门以增加获奖的概率，这个问题引发了很多争议和讨论。

3. 红绿灯问题红绿灯问题是指在一个红绿灯路口，红灯亮的时间为60秒，绿灯亮的时间为90秒。

假设一个人随机到达这个路口，他等待的时间有多长？这个问题可以用概率统计的方法来解答，并且可以拓展到更复杂的情况。

4. 奇偶校验奇偶校验是一种常用的错误检测方法，常用于计算机数据传输中。

它利用二进制数中1的个数的奇偶性来检测错误。

比如，一个字节中有奇数个1，则奇偶校验位为1，否则为0。

这个案例可以帮助我们理解错误检测的原理和应用。

5. 投掷硬币投掷硬币是统计学中最基础的实验之一。

通过投掷硬币的结果，我们可以计算出正面和反面出现的概率，进而进行概率分布的推断和假设检验。

6. 高尔夫球洞问题高尔夫球洞问题是指在一个高尔夫球场上，有一个球洞和一个标杆。

如果球员将球随机击打，求平均击打到球洞的距离。

这个问题可以通过统计模拟和概率分布计算来解答。

7. 疾病筛查疾病筛查是统计学在医学领域的重要应用之一。

通过对人群进行检测和筛查，可以计算出疾病的发病率、敏感性、特异性等指标，对疾病的预防和控制起到重要作用。

8. 艾滋病传播模型艾滋病传播模型是指通过数学模型和统计方法，研究艾滋病在人群中的传播规律和预测。

通过对不同人群的感染率、传播速度等指标的估计，可以制定有效的防控措施。

9. 电影评分电影评分是一种常见的统计学应用，通过对观众的评分和评论进行统计分析，可以计算出电影的平均评分、评分分布、观众对电影的满意度等指标，对电影的推广和市场研究具有重要意义。

生日相同问题结构体
《生日相同问题》
在人群中，不太可能会有两个人的生日相同，但当人数增加到一定程度时，可能性就会变得更高。

这个现象被称为“生日相同问题”。

生日相同问题是指在一群人中，至少有两个人的生日相同的概率。

虽然这听起来不太可能发生，但根据概率论的计算，只需要23个人就有50%的概率至少有两个人生日相同。

这个概率远远
超出了大多数人的想象，甚至被称为“生日悖论”。

这个问题的背后有一个简单的解释：不同的人之间生日相同的可能性并不是独立的，而是相互关联的。

在一个有限的365天中，随着不断增加的人数，生日相同的可能性也随之增加。

生日相同问题的思考不仅仅是一种数学上的猜想，更是对概率论的实际应用。

在实际生活中，我们可能会在朋友圈或工作场所中遇到这样的情况，甚至自己身边的人中也会有出现生日相同的情况。

因此，了解生日相同问题不仅可以帮助我们更好地理解概率论，还能让我们更加理性地面对生活中的各种奇遇和巧合。

这样的思考和认识也能让我们更加珍惜和享受每一个特殊的生日，因为它的独特性可能远远超出了我们的想象。

经典概率问题
以下是经典概率问题的相关参考内容：
1. 生日悖论问题：
生日悖论问题指的是在一个房间里，至少有两个人生日相同的概率有多大？
答案：在23人的房间里，至少有两个人生日相同的概率为50%。

在70人的房间里，概率上升至99.9%。

2. 抛硬币问题：
在抛一枚硬币时，出现正面和反面的概率各是多少？
答案：出现正面和反面的概率都是50%。

3. 掷骰子问题：
在掷一颗标准骰子时，出现每个数字的概率各是多少？
答案：出现每个数字的概率都是1/6。

4. 红球与白球问题：
在一个袋子里有10个红球和10个白球，从中抽出一个球后再放回，重复抽球直到抽出两个同色的球为止。

问至少需要抽多少次？
答案：需要抽至少4次，才能保证抽出两个同色的球。

5. 斯特林公式问题：
斯特林公式的表达式是什么？
答案：n!可以近似表示为√(2πn)(n/e)^n，其中n为正整数。

6. 二项分布问题：
二项分布指的是什么？
答案：二项分布指的是在进行重复实验时，每次实验只有两种结果，并且每种结果出现的概率相等的情况下，成功次数的概率分布。

同一天生日的概率问题姓名：xx班级：06级电子商务一班学号：0125上课时间：星期一据国外媒体报道，数学经常会让聪明人感觉自己笨得不行，有时甚至会让他们很生气。

事实上，数学本身非常有趣，它是我们日常生活的一部分，每个人都能从中获得享受。

只不过在课堂上，数学被一些死板的老师教死板了。

以下就是英国《每日邮报》最近公布的日常生活中一道趣味数学：同一天过生日的概率假设你在参加一个由50人组成的婚礼，有人或许会问：“我想知道这里两个人的生日一样的概率是多少？此处的一样指的是同一天生日，如5月5日，并非指出生时间完全相同。

”也许大部分人都认为这个概率非常小，他们可能会设法进行计算，猜想这个概率可能是七分之一。

然而正确答案是，大约有两名生日是同一天的客人参加这个婚礼。

如果这群人的生日均匀地分布在日历的任何时候，两个人拥有相同生日的概率是97%。

你没有看错，的确是97%。

这似乎超出了很多人的想象。

认为这不可能有这么高的概率。

开始我也这么认为我问过很多人，都觉得不好算。

简化点问是否有50%？答没有，再问有没有20%，也还是觉得没那么高。

当我告诉答案是96.5%时，都表示不相信。

而事实上，当有50个学生时，答案确实是96.5%；有59个学生更是高达99.1%，有47个是94.8%，有35个是80.5%，而当有23个时，概率就刚好超过50%，可以进行赔率为1:1的赌博了。

另一方面，要是以普通约为50人的班做对象，按1:10的赔率赌博也是个赚字。

看到这些答案吃惊吗?不信的话可以做验证，下面有两个方法：第一个是实验验证，找多个班的学生生日资料，查查是不是有同一天过生日的，计算有同一天过生日的数量占总数的百分比。

当然也不必限定一定是学生，只要是能找到生日资料的任何人群都可以，如亲人朋友、战友、网友、同村的、同楼的等等，有生日记载的历史人物也可以，只要按一定的数量组成要考查的群体就行。

第二个是实验数学方法验证。

毕竟要找那么多人的生日资料不是很容易办到的。

生日悖论外传：任取两个人生日相同的概率是50%对原题的误读，有时竟会产生一些更有意思的问题。

果壳问答上，网友 qxx 提问说：一个房间里面有很多人，我想让房间里面任意两个人的生日相同的概率是 50% 的话那房间里面应该最少有多少人？当然，几乎可以肯定，提问人原本是想说“至少两个人”的，而问题的答案就是 23 ——生日悖论带来的惊人的答案。

不过，如果把“至少两个人”误说成“任意两个人”，题目意思就完全变了，并且变得明显更有意思了。

大家很快便会想到，如果任取两个人，他们的生日相同的概率恰好是 50% ，那么房间里最少有四个人，其中三个人的生日是同一天，另外一个人的生日跟他们都不同。

从四个人里选出两个人有 6 种方案，选出生日相同的两人则有 3 种方案，恰好是 6 的一半。

继续看下去之前，大家不妨来猜猜看，这个问题还有其它的解吗？下一个解有多大？问题的本质就是，把 n 拆分成 n1+ n2+ … + nk，使得 C(n1, 2) + C(n2,2) + … + C(nk, 2) 正好等于 C(n, 2) 的一半。

下一个解发生在 n = 9 的时候，其中有 6 个人拥有共同的生日，另外 3 个人拥有另一个共同的生日。

我们不妨把这个解简记作 9 ＝ 6 + 3 。

我用 Mathematica 进行了一些简单的搜索，得到了 n < 40 时全部的解：4 = 3 + 19 = 6 + 313 = 9 + 3 + 116 = 10 + 617 = 12 + 2 + 2 + 120 = 14 + 3 + 2 + 121 = 15 + 1 + 1 + 1 + 1 + 1 + 124 = 17 + 2 + 2 + 1 + 1 + 125 = 15 + 1028 = 19 + 6 + 3 = 18 + 9 + 129 = 20 + 5 + 3 + 132 = 22 + 6 + 2 + 233 = 23 + 5 + 2 + 1 + 1 + 136 = 25 + 6 + 1 + 1 + 1 + 1 + 1 = 25 + 4 + 4 + 3 = 24 + 9 + 3 = 21 + 1537 = 26 + 4 + 2 + 2 + 1 + 1 + 1 = 26 + 3 + 3 + 2 + 2 + 1当 n ＝ 40, 41, 44, 45, 48, 49 时也是有解的，解的个数分别为 5, 3, 6, 3, 5, 8 。