当前位置：文档之家 › 第6章单相流体对流换热汇总

第6章单相流体对流换热汇总

  • 格式：doc
  • 大小：823.00 KB
  • 文档页数：49

下载文档原格式

  / 49

合集下载

传热学6-单相流体对流换热

传热学6-单相流体对流换热



三. 管内层流强迫对流换热关联式
实际工程换热设备中，层流时的换热常常处于 入口段的范围。可采用西得和塔特公式。
Nu f 1.86 Re
1/ 3 f
d 1 / 3 f 0.14 Pr ( ) ( ) l w
1/ 3 f
定 性 温 度 为 流 体 平 均 温 度 tf （ μ w 按 壁 温 tw 确定），管内径为特征长度，管子处于均匀壁 温。 实验验证范围为：
ud 2 0.02 4 4 Re 4 . 97 10 10 6 v 0.805 10
因为是加热流体n=0.4
6 2
（3）计算准则，选定公式。
Nu 0.023Re0.8 Prn
（4）代入公式计算，不考虑修正
Nu 0.023 4.9710
Nu 258.5 0.618 h 7987W /( m2 oC ) d 0.02
其中：温度修正系数（液体被加热） f ct w
0.11
可以不修正
786 .7 10 764 .4 10 6
6 0.11
1.003
h
Nu f d
315.766 0.62 9322W 2 m K 0.021
流动方向上的坐标无关。
在入口段，局部对流换热系数随流动方向而变化 层流：随着流动方向而增加 , h 紊流：开始同层流，进入紊流后 h
入口段长度
层流 紊流
l l
d d
0.05 Re P r 60
常壁温
满足上述条件时入口效应可以忽略不计
紊流时，若L/d<60则须考虑入口段的影响
t t' w f ln t t '' w f ln t ' t ''

第六章 单相流体对流换热

第六章 单相流体对流换热

2
2.流动充分发展段层流和湍流的判断 • 层流： Re 2300 • • 过渡区：
2300 Re 10000
旺盛湍流： 10000 Re
3
3. 热入口段和充分发展段的判断（表面传热系数的变化）
（定壁温）充分发展段为层流或湍流的热入口段长度:
l / d 0.05 Re Pr
l / d 60
6 2
Pr f 3.54, , f 64.8 102 W /( m C ); 以t w 90C 查 w 314.9 106 kg /( m s )
Re f uf d 2 0.12 4 43.1655 10 6 0.556 10
M=0.0417kg/s,管长2.6m,空气进口温度
tf ’=30,管壁温度保持tw=250，试计算该换 热器的表面传热系数。（讨论）
32
第二节 流体横向绕流管束的换热
一、流体横向绕流单管（或柱）时的对 流换热计算
二、流体横向绕流管束的对流换热计算
33
一、流体横向绕流单管（或柱）流动时 的对流换热计算
24
Nu f
由管内流体的能量平衡可得
hA(tw t f ) qmc pf (t f tf )
1 2 h dL( t w t f ) d f u f c pf (t f tf ) 4
8596 20 10 3 (40
23
水被加热，取 m 0.4
Nu f 0.023 Re Pr
0.8 f
0.4 f 4 0.8 0.4
0.023 (4.97 10 ) (0.702)
h
287
f

1 第6章-单相流体对流换热及准则关联

1 第6章-单相流体对流换热及准则关联
排列方式及管间距：影响流速 管排数：当流过主流方向的管排数达到一定数目后，流动
与换热会进入周期性充分发展阶段。在该局部区域，每排
管子的平均表面传热系数保持为常数。
先给出不考虑排数影响的关联式，再采用管束排数的因素 作为修正系数。
物性修正：流体进入管束的温度变化较大时，需考虑。可 0.25 采用物性修正因子 Pr f Prw
衡式：
hm AΔt m = q m c p (t f - t f )
式中， q 为质量流量；
m
tf、tf
分别为出口、进口截面上的平均温度
20
Δt m 按对数平均温差计算：
t m
tf tf tw tf ln tw tf
当流体进口截面与出口截面的温差比在0.5～2之间时， 可用算术平均温差代替对数平均温差。
15
换热特征：入口段的热边界层薄，表面传热系数高。 层流入口段长度:
l / d 0.05 Re Pr 湍流入口段长度 l / d 60
层流
湍流
16
换热特征
热边界层同样存在入口段与充分发展段， 在进口处，边界层最薄， h
x
具有最高值，随后降低。
在层流情况下，h x趋于不变值的距离较长。 在紊流情况下，当边界层转变为紊流后， h x 将有一些回
44
曲面的加速降压段：流体有足够动能继续前进。 曲面的降速升压段：动能要转化为势能，又要克服粘滞力的 影响，动能损耗大。其结果是从壁面的某一位置0开始速度梯 度达到0，壁面流体停止向前流动，并随即向相反的方向流动。 以致从0点开始壁面流体停止向前流动，并随即向相反的方向 流动，该点称为绕流脱体的起点 ( 或称分离点 ) 。
tw tf tw tf tw tf 0.5 2,tm tw tf 2

第6章-单相流体对流换热

第6章-单相流体对流换热
过渡区： 旺盛紊流：
Re 2300
2300 Re 10
4
Re 10
4
与外掠平板（板流）相比，
管内流动（管流）出现4个新的特征：
1. 进（入）口段、充分发展段； 2. 管内流体平均速度、平均温度； 3. 物性场的不均匀性 4. 几何特征
外掠平板边界层
1. 进（入）口段、充分发展段
Pr = 1
实验验证范围： Re 3.6 103 ～ 9.05 105 , f 均匀tw 边界 实验验证范围：
Nuf 5.0 0.025Pef
Pef 100
0.8
定性温度——流体平均温度，特征长度——din
Ref Prf f 管子很 ，且 l / d w 3. 层流 层流充分发展段对流换热的分析解结果很多。
第六章 单相流体换热分析
Convection of Single Phase Fluid
主要内容
单相流体对流换热（自由运动、强制对流）
§6-1 §6-2 §6-3
管内受迫对流换热 外掠圆管对流换热 自然对流换热
§6-1 管内受迫对流换热（管流）
一、一般分析
有层流、紊流之分


层流：
0.45
Tf 0.6 Prf 1.5,0.5 1.5,2300 Ref 104 Tw
液体
Nu f 0.012 (Ref
0.87
280) Prf
0.4
d 2 / 3 Prf 1 ( ) l Pr w
0.11
Prf 1.5 Prf 500,0.05 20, 2300 Ref 104 Prw

06第六章 单相流体对流传热特征数关联式

06第六章 单相流体对流传热特征数关联式
⎛ ηf 对于液体： ct = ⎜ ⎜η ⎝ w ⎞ ⎟ ⎟ ⎠
n
⎧加热：n = 0.11 ⎨ ⎩冷却：n = 0.25 ⎞ ⎟ ⎟ ⎠
0.55
⎛ Tf 气体被加热： c t = ⎜ ⎜T ⎝ w
特例——烟气冷却时。
1－等温， 2－液体被冷却或气体被加热， 3－液体被加热或气体被冷却
气体被冷却：ct=1
d R
3
⎛d ⎞ 液体： cR = 1 + 10.3⎜ ⎟ ⎝R⎠
第 1 页
共 7 页
第六章 单相流体对流传热特征数关联式 ③温差的影响 温度修正系数 cf 式（6-5b） 温度场影响速度场（通过影响粘度） 液体 t↑,η↓ 曲线 3 气体 t↓,η↓ 液体被加热,气体被冷却 气体 t↑,η↑ 曲线 2 液体 t↓,η↑ 液体被冷却，气体被加热
作业： 6-4
§6-2 外掠物体时的强迫对流传热
工程上，常见的另一种对流换热形式就是外掠物体时的强迫对流换热，如电 厂中锅炉烟气横掠过热器和省煤器管束，空气纵掠机翼等等。这一节，我们将介 绍这种强迫对流换热的计算式。 δ
一、纵掠平壁
流体沿平板流动时，一般情况下是在平 板前缘开始形成层流边界层，然后过渡
h=B
λ0.6 (ρc )0.4 ν 0.4
A,B 由物性决定，流体一定它们仅是流体平均温度和压力的函数。有计算式 （6-7,6-8） 。 例：水流过长l=5m，壁温均匀的直管时，从tf΄=25.3℃被加热到tf˝=34.6℃，管子 的内径d=20mm，水在管内的流速为 2m/s，求表面传热系数h。 l 5 解：① = = 250 > 50 是长直管。 d 0.02 1 1 ②水的平均温度 t f = (t 'f + t "f ) = (25.3 + 24.6 ) = 30 ℃，以此为定性温度，查附 2 2 录 7(P322)得 λf=0.618 W/(m·K)， vf=0.805×10-6 m2/s， Prf=5.42， ρ=995.7 kg/m3， cp=4.174 kJ/(kg·K) ud 2 × 0.02 ③ Re = = = 4.97 × 10 4 > 10 4 紊流 ν 0.805 × 10 −6 用式（6-5）求 h

传热学课件第六章--单相流体对流换热

传热学课件第六章--单相流体对流换热



1 3
紊流： Nu 4.69 Re
0.27
Pr
0.21
Gr
0.07

d L
0.36
其中Gz=Re· Pr· d/L 为格雷茨（Graetz）准则数，定性温度 依然是平均温度tm。
第一节 管内受迫对流换热
一、定性分析（基本概念）
2>.对于换热状态
Re>104紊流
入口段 h h hx
充分发段
h∞
x/d
x↑→（层流）↑→hx↓，x↑↑→边界层转入紊流→ c↓→ hx↑， x↑↑↑→ c不变而↑→ hx↓，x↑↑↑↑→ c不变且=R→ hx不变。 此时hx不变的距离（即进口段长度）：L/d=10～45
第三节
自 然 对 流 换 热
三、自然对流与受迫对流换热并存的混合对流换热
当Gr/Re2≥10时：作纯自由流动 当Gr/Re2≤0.1时：作纯受迫流动 当0.1<Gr/Re2<10时：作混合流动 横管内混合对流换热可按下式估算：
f 层流： Nu 1.75 w
0.14
1 Gz 0.012 Gz Gr 3 4 3
q
he
e t w1 t w 2 t w1 t w 2
e/=Nu 故e/即为有限空间自由对流换热的努谢尔特数。 另外一般地说： 对于：水平夹层：Gre<1700时 均作纯导热处理 垂直夹层：Gre<2000时 此时可认为夹层内无环流产生。
第三节
自 然 对 流 换 热
一、无限空间自由流动换热（大空间自然对流）
指热（冷）表面的四周没有其它阻得自由对流的物体存在。 一般准则方程式可整理成： Nu=f（Gr· Pr） 一般Gr· Pr>109时为紊流，否则为层流。 对于常壁温的自由流动换热，其准则方程式常可整理成： Num=C（Gr· Pr）mn C、n可参见表6=5，注意使用范围、定型尺寸、定性温度。 令：Ra=Gr· Pr Ra为瑞利准则数。 既适用常壁温也适用常热流边界的实验准则方程式，常见的 为邱吉尔（Churchill）和朱（Chu）总结的式6-19，20。

第6-单相流体对流换热.

第6-单相流体对流换热.
特征长度：管内径。
适用的参数范围：Ref 104 P r0.7~1670l0/d60
格尼林斯基公式：
对于气体
Pr T 0 . 6 f 1 . 5 , 0 . 5 f 1 . 5 , 2 3 0 0 R e f 1 0 4
Tw
0 . 4 5
Nu d T f0 . 0 2 1 4 ( R e f 0 . 8 1 0 0 ) P r f0 . 4 1 () 2 / 3 f
dx cpumR
d(twtf)x 2hx dx
(twtf)x cpumR
常壁温时，断面流体平均温度按对数规律变化。
常壁温时，断面流体平均温度按对数规律变化。 常壁温时流体与壁面间的温度差——对数平均温差
tm (tw lntftt)ww (tttwff tf)tln ttt
常壁温时全管长流体平均温度
当r =R时：
tw(x)t(x,r)
rtw(x)tf
(x)
rR
t rrR
twtf
qw
h const qw
h
结合 x ttw w ((x x)) tt(fx(,x r)) x ttw w ttf 0
对照图示，管入口段（无论是层流或紊流），局部换热系 数h x沿管长降低，这部分长度内，局部换热系数h x与全长上 的平均换热系数h不同。充分发展段，h x和h都趋于定值。 在后面提供的经验公式均是指全管长上的平均换热系数h。
C. 点的无量纲温度与x无关
管内流动时热入口段长度范围
层流 紊流
2、管内流体平均速度和平均温度
A 管内流体平均速度:
管内流体平均速度
um
V f
f
R
udf u2rdr
umV f 0R2 0 R2

第6章单相流体对流换热

第6章单相流体对流换热

2）管内流体平均温度

管断面流体平均温度 全管长流体平均温度
定性温度
①管断面流体平均温度（按焓值计算） ② 全管长流体平均温度（由热平衡关系计算）
传热学 Heat Transfer
不同边界条件下全管长流体平均温度 （常热流边界和常壁温边界）

q=const时，dtf/dx=const

从入口开始，tf呈线性变化，全管长平均温度为进出口
一、 外掠单管
横掠单管：流体沿着 垂直于管子轴线的方 向流过管子表面。流 动具有边界层特征， 还会发生绕流脱体。
传热学 Heat Transfer
1 、 流动边界层的形成与发展
①流体的压强大约在管的前半部递降，即dp/dx<0,而
后又回升，即dp/dx>0
②边界层内流体的动能变化与压强的变化相对应； ③脱体绕流产生 衡量脱体绕流的程度：速度 衡量脱体绕流的准则数：Re
传热学 Heat Transfer
第六章
单相流体对流换热
传热学 Heat Transfer
本章教学内容
6-1 管内受迫对流换热 6-2 外掠圆管对流换热 6-3 自然对流换热
传热学 Heat Transfer
§6-1 管内流体受迫对流换热
一、一般分析
受迫在管内对流换热时，应考虑管内流动及换热的 4 个特
是先用定性温度确定物性，再可确定计算式中的准则数。
f 3.15 104 N s m 2 ; Pr 1.95
t w =115℃： w 2.48 10 4 N s m 2
传热学 Heat Transfer
则 Ref um d
f
0.017 0.85 4 4.43 10 6 0.326 10

第6章 单相流体对流换热

第6章 单相流体对流换热
冷却流体
Nu f 0.023Re Pr
0.8 f
0.4 f
Nu f 0.023Re0f.8 Prf0.3
l / d 10
适用条件：中等以下温度差
Ref>104 Prf=0.7~160
2014-7-8
定性温度取全管长平均温度tf，定型尺寸为管内径
17
传热学

（2）西得－塔特公式
Nu f 0.027Re Pr ( f / w )
传热学
传热学（第五版）
Heat Transfer


主讲教师： 李志生
广东工业大学 土木与交通工程学院
2014-7-8
1
第6章
单相流体对流换热
传热学
本章主要内容
1、管内受迫对流换热 2、外掠圆管对流换热 3、自然对流换热



2014-7-8
3
传热学
第一节 管内受迫对流换热


f f
11
c tudf
p
R
传热学
流体沿管长焓值的变化等于它与管壁的换热量
d hx tw t f x 2Rdx c pumR 2 dt f
d q 2Rdx
dt f 2q dx c pum R
或
12
dt f dx

2hx t w t f x
2014-7-8
图6-15 有限空间自然对流换热
传热学
复习


流体的流动状态可分为哪几种？哪种换热效果好？ 对流按起因可分为哪两类？哪种换热效果好？
间导热热阻小 ) h (流体内部和流体与壁面 、c p h (单位体积流体能携带更多能量)

传热学讲义对流换热——第六章

传热学讲义对流换热——第六章

第六章 单相流体对流换热及准则关联式第一节 管内受迫对流换热本章重点：准确掌握准则方程式的适用条件和定性温度、定型尺寸的确定。

1-1 一般分析),,,,,,,,(l c t t u f h p f w μαρλ=流体受迫在管内对流换热时，还应考虑以下因素的影响：① 进口段与充分发展段，② 平均流速与平均温度，③ 物性场的不均匀性，④ 管子的几何特征。

一、进口段与充分发展段1．流体在管内流动的主要特征是，流动存在着两个明显的流动区段，即流动进口（或发展）段和流动充分发展段，如图所示。

（1）从管子进口到边界层汇合处的这段管长内的流动称为管内流动进口段。

（2）进入定型流动的区域称为流动充分发展段。

在流动充分发展段，流体的径向速度分量v 为零，且轴向速度u 不再沿轴向变化，即：0=∂∂xu， 0=v 2．管内的流态（1）如果边界层在管中心处汇合时流体流动仍然保持层流，那么进入充分发展区后也就继续保持层流流动状态，从而构成流体管内层流流动过程。

2300Re <用νdu m =Re 判断流态, 式中 m u 为管内流体的截面平均流速， d 为管子的内直径，ν为流体的运动黏度。

（2）如果边界层在管中心处汇合时流体已经从层流流动完全转变为紊流流动，那么进入充分发展区后就会维持紊流流动状态，从而构成流体管内紊流流动过程。

410Re >（3）如果边界层汇合时正处于流动从层流向紊流过渡的区域，那么其后的流动就会是过渡性的不稳定的流动，称为流体管内过渡流动过程。

410Re 2300<<3．热进口段和热充分发展段当流体温度和管壁温度不同时，在管子的进口区域同时也有热边界层在发展，随着流体向管内深入，热边界层最后也会在管中心汇合，从而进入热充分发展的流动换热区域，在热边界层汇合之前也就必然存在热进口区段。

随着流动从层流变为紊流， 热边界层亦有层流和紊流热边界层之分。

热充分发展段的特征对常物性流体，在常热流和常壁温边界条件下，热充分发展段的特征是：)(1x f t f =及)(2x f t w =与管内任意点的温度),(r x f t =组成的无量纲温度⎪⎪⎭⎫⎝⎛--x f x w w t t t t ,,x ,随管长保持不变，即： 0,,x ,=⎪⎪⎭⎫ ⎝⎛--∂∂x f x w w t t t t x 式中，t —管内任意点的温度，),(r x f t = ⇒xf x w w t t tt ,,x ,--仅是r 的函数。

第6章 单相流体对流换热及准则关联式

第6章 单相流体对流换热及准则关联式

d
CCE BEFE
(b)
紊流
入口段
充分发展段
Re u m d /
流态判断
(充分发展段)
Hale Waihona Puke Re 2300 4 过渡区： 2300 Re 10 4 旺盛湍流： Re 10
层流： 层流充分发展段
u 0 0 x
截面平均速度
二次曲线
速度分布
Velocity profile
(充分发展段)
沿管长积分
t 2h exp( x) t c p u m R
流体与壁面间 的温度差沿管 长按对数曲线 CCE BEFE 规律变化
t 2 当 t
(t w t f ) (t w t f ) t t t m (t w t f ) t ln ln t (t w t f )
Nothing is impossible to a willing heart.
第六章 单相流体对流换热及准则关联式
Chapter Six Empirical and Practical Relations for Forced-Convection Heat Transfer of single phase
一、换热进口段长度
◆常物性流体层流热进口段长度 Lh 0.05 Re Pr tw=const d qw=const Lh 0.07 Re Pr d
Pr数非常大的油类介质， 它们的热入口段将会 很长，可达管径的数 百倍，以至于对实用的 换热设备来说，可 能直到出口也没达 到热充分发展状态（但 速度分布早已 达到充分发展状态了）。
管内对流属于有界流动，它与无 界流动的最大区别在于，它的边界层 的形成和发展受到壁面的限制和重要 影响。它的流动和换热情况都呈现出 外部流动所不具有的一些特征。

《传热学》第六章 单相流体对流换热

《传热学》第六章 单相流体对流换热
影响h的因素分析：
2. 层流换热
西得和塔特常壁温公式：
对于长管，h近似为常数：
3.过渡流换热——格尼林斯基关联式 4.粗糙管壁的换热 ——采用类比原理进行分析
根据类比率得出的准则方程：
其中：
摩擦系数Cf的计算：
ks——粗糙点的平均高度
粗糙度增加对h的影响
紊流 层流
凹处形成涡流， h增大
换热面积增大， h增大
自然对流引起 的雷暴天气
一、无限空间自然对流换热
边界层速度 变化规律：
边界层温度 变化规律： 局部对流表面传热系数hx沿竖壁变化规律—— 在层流段逐渐降低，紊流段后增大，达到旺盛紊流时保持不变
X方向动量方程：
稳态流动： 体积力仅为重力： 根据量纲分析：
X方向动量方程简化为：
将：
代入上式，得：
X方向动量方程变为：
凹处流动不良， h减小
h增大
h不变
不锈钢椭圆管
椭圆管与同周 长圆管相比较
优点：换热强 缺点：阻力大
椭圆管换热器
第二节 外掠圆管对流换热
一、外掠单管
脱体分离点—— 流体产生与原流动方向 相反的回流时的转折点
分离点与流 速的关系：
——不产生脱体 ——层流，脱体点80°~85 ° ——紊流，脱体点140 °左右
二、管内受迫对流换热计算 管内对流换热能量守恒关系式：
1. 紊流换热
迪图斯－贝尔特公式：
定性温度：全管长流体平均温度tf
定型尺寸：管内径
迪图斯－贝尔特公式适用范围：流体和壁面温度差不很大，
西得和塔特公式：
——适用于流体与管壁间温差较大情况
非圆形管修正：采用当量直径
弯管修正：圆管结果乘以修正系数 （R为螺旋管曲率半径）

1 第6章-单相流体对流换热及准则关联

1 第6章-单相流体对流换热及准则关联
1
2
3
4
5
6
7
8
9
10
11Leabharlann 121314
第六章 单相流体对流换热及准则关联式
6.3 管内受迫强制对流流动与换热的一些特点 1 、两种流态 层流区： Re<Rec =2300 ；
Re u m d
一般多取截面平均流速
过 渡 区 ： Re=2300-104 ；
紊流区： Re>10
Nu f 0.021Re
0.8 f
Pr
0.43 f
Pr f Prw
0.25
定性温度为流体平均温度 tf ，管内径为特 征长度。 实验验证范围为： l / d 50，
Pr f 0.6～700,
Re f 10 ~ 1.75 10 。
4 6
30
格尼林斯基（Gnielinski）公式是迄今为止计算准确度最 高的关联式。考虑了温差、长径比，也适用于非圆形截面 通道，有较高的计算精度。 说明：
t m
tf tf tw tf ln tw tf
当流体进口截面与出口截面的温差比在0.5～2之间时， 可用算术平均温差代替对数平均温差。
tw tf tw tf tw tf 0.5 2,tm tw tf 2
0.5
对液体 ct f w


m
受热时 被冷却
m 0.11
m = 0.25
25
（2）入口段的影响
当管子的长径比l/d<60时，属于短管内流动换热，
入口段的影响不能忽视。此时亦应在按照长管计算
出结果的基础上乘以相应的修正系数 ，入口段的

第六章单相流体对流换热及准则关联式_传热学汇总

第六章单相流体对流换热及准则关联式_传热学汇总
当雷诺数处于Re<2300<104的范围内时，管内流动属于 层流到紊流的过渡流动状态，流动十分不稳定。工程上常常 避免采用管内过渡流动区段。
例题 5-1 在一冷凝器中，冷却水以 1m/s 的流速流过内径为 10mm 、长 度为 3m 的铜管，冷却水的进 、出口温度分别为 15℃和65℃，试计算管内的表面传热系数。 解： 由于管子细长，l/d较大，可以忽略进口段的影响。冷 却水的平均温度为
定性温度为流体平均温度tf ，管内径为特征长度。
c.米海耶夫公式：
Nuf 0.021 Ref
0.8
Prf
0.43
定性温度为流体平均温度tf ，管内径为特征长度。 实验验证范围：
Prf Prw
0.25
l / d 50, Re f 104 ~ 1.75106 , Prf 0.6 ~ 700
流动充分发展区段的特征:
u 0, v 0 (u为轴向速度,v为径向速度) x
(2) 换热也存在着两个明显的区段，即热进口（或发展）区 段和热充分发展区段, 且常物性流体在热充分发展段的表面 传热系数保持不变,而入口段的热边界层薄，表面传热系数高。 热充分发展区段的特征:
t w t h ( t w t f ) 0, const x
' "
t m (t ' t " ) /(ln t ' t " )
(
' " , t 出口端流体与管壁温度 ) t 进口端流体与管壁温度
3、物性场不均匀
当流体与管壁之间的温差较大时，因管截面上流体温度变 化比较大，流体的物性受温度的影响会发生改变，尤其是流 体黏性随温度的变化导致管截面上流体速度的分布也发生改 变，进而影响流体与管壁之间的热量传递和交换。

第六章单相流体对流换热

第六章单相流体对流换热

1Chapter 6 Single-Phase Fluid Convection (单相流体对流换热)The discussion and analysis of Chapter 5 have shown how convection heat transfer flow over a flat plate (外掠平板) may be calculated. However it is not always possible to obtain analytical solutions (分析解)to convection problems.不能用理论方法求解时，靠实验方法获得换热关联式。

单相流体换热包括：受迫对流、自然对流、混合对流。

26-1 Forced-Convection Heat Transferin a Tube(管内受迫对流换热)1-1 Analysis for flow in a tube(管内流动分析)1.1 entry region and fully developed region in a tube (进口段与充分发展段)1.Flow boundary layer(流动边界层)进口段：流体进入管口，经历一段距离，管断面流速分布和流动状态才达到定型。

充分发展段：流态定型，流动达到充分发展。

In a tube,the Reynolds number (Re ) is again used as acriterion (标准)for Laminar and turbulent flow.entry regiondeveloped region Figure 6-1Thefluid and surface is approximately注意事项：间的温度差及其平均温度。

Isothermal flow等温流Liquid cooling,gas heatingLiquid heating ,gas cooling221-2 heat transfer for forced-convection of tube flow(管内受迫对流换热)2.1 Heat transfer in fully developed turbulent flow(紊流换热)The empirical relations for forced-convection heat transfer(受迫紊流换热准则关联式)1. A traditional expressions for calculation of heattransfer in fully developed turbulent flow in smooth tubes is that recommended by Dittus and Beolter (迪图斯—贝尔特)n fff Nu PrRe023.08.0=nm C Nu PrRe =Where C , n and m are constants to be determined from the experimental data.23For heating of the fluid )(f w t t >For cooling of the fluid)(f w t t <With moderate temperature differences between wall andfluid conditions, ExampleApplicable ranges ：长径比160~7.0Pr;10Re ;10/4=>>>ffd l Film temperature ：the mean bulk temperature of fluid (定性温度：全管长流体平均温度)Characteristic length ：inner diameter of tube Ct air °=Δ50Ct liquids °≈Δ20=0.4n=0.3n(定型尺寸：管内径d )0.81/30.140.023Re Pr(/)f f ff w Nu μμ=()()20.80.40.2530.0214Re 100Pr1/(/)f fff w Nu d l T T ⎡⎤=−+⎢⎥⎣⎦()()20.870.40.1130.012Re280Pr1/(Pr /Pr )f fff w Nu d l ⎡⎤=−+⎢⎥⎣⎦It strengthens the heat transfer,so4.04.02.08.0023.0−−−=adu h λν),,,,,(2.04.08.04.06.08.0−−=dc u f h pμρλLaminar flowThe heat transfer is not influenced by surface roughness35The heat transfer is increased by the surface roughness in turbulent flow region.讨论：粗糙点能增强换热，缩小换热设备面积，节约设备投资，并带来其他经济效益，但流动阻力也随之增加，致使泵的功率消耗增加，运行费用增加。

06第六章 单相流体对流传热特征数关联式

06第六章 单相流体对流传热特征数关联式

第六章单相流体对流传热特征数关联式三、横掠管束时的强迫对流传热1．流动情况①排列方式叉排好，后受前尾流扰动大。

②管排数
h21=h20>h19>h18>…>h1 ∴给出的是z≥20 时的式子，如z<20 乘cz<1 2．换热计算 Nu f = c Re m f , max 管束的排列方式⎛ Pr f Pr ⎜⎜ Pr ⎝ w n f ⎞⎟⎟⎠ k ⎛ s1 ⎜⎜s ⎝ 2 ⎞⎟⎟ cϕ c z ⎠ p (6-23 按式子要求查系数，定性温度，特征尺寸，特征速度等。

作业： 6-18 §6-3 自然对流传热一、概述前面介绍的都是在外力作用下使流体流动的强迫对流传热，工程应用中还有另一种靠流体浮升力使流体运动的自然对流传热，如太阳能集热器的空气夹层，热力管道散热等（绪论例 1-2：1721W 自然对流，例 1-3：3051 W 辐射）。

1．定义：浮升力⎧大空间自然对流传热2．分类：⎨⎩有限空间自然对流传热二、大空间自然对流传热（与有限相对）1．定义：传热面上边界层的形成和发展不受周围物体的干扰。

2．边界层的发展第 6 页共 7 页
第六章单相流体对流传热特征数关联式 3．换热计算会查书或其他资料套。

三、有限空间的自然对流传热（概念）定义：传热面上边界层的形成和发展受周
围物体的干扰。

（不局限于几何条件，主要看边界层）H δ δ H < 0.3 第 7 页共 7 页。

传热学第六章单相流体对流传热特征数关联式

传热学第六章单相流体对流传热特征数关联式
当温差超过推荐的幅度值后，流体热物性将发 生变化，从而对换热产生影响。
对于液体：主要是粘性随温度而变化。 对于气体：除了粘性，还有密度和导热系数等。
修正方法：
ct
f w
n，或ct
Tf Tw
n
，或ct
Prf Prw
n
传热学 Heat Transfer （2）非圆形截面通道
对于方形、椭圆形、环形等形状的截面情况，可
定是否需要考虑修正项 f
0.14 w
。可以首先根据
冷却水的温升确定换热量 qmct t ，再用上
面计算的表面传热系数h和牛顿冷却公式求解壁温。
传热学 Heat Transfer
6-2 外掠物体时的强迫对流传热
按照概述中的分类外部 流动的强制对流换热主要 有横掠平板、外掠单管和 外掠管束等情况。
Ref
104 ;
0.7 Prf
160 ;
l d
60
气体：t 50 ℃

油：t 10 ℃
水：t 30 ℃
式中取流体平均温度作为定性温度；取管子内径d
为特征尺度；取截面的平均流速作特征速度。
传热学 Heat Transfer 2. 迪图斯-贝尔特关联式应用范围的扩展 （1）温差超过推荐的幅度值
传热学 Heat Transfer
三、横掠管束换热实验关联式
1. 流动和换热的特征
管束的排列方式有顺排和叉排两种形式。叉排中的 流动扰动比顺排时要剧烈，因此换热也较强。此外， 管束的间距s1和s2及管排数也影响换热强度。
顺排
叉排
传热学 Heat Transfer
2. 平均表面传热系数 h 计算的关联式
Nu f
c
Re

单相流体对流换热及其准则关联式

单相流体对流换热及其准则关联式

的流速。
实验验证范围： Ref 2000 ~ 40000。
C和m的值见下表。
对于排数少于10排的管束，平均表面传热系数可在上
式的基础上乘以管排修正系数 n 。
h nh n 的值引列在下表。
4. 特征速度及定性温度的确定
特征速度一般多取截面平均流速。 定性温度多为截面上流体的平均温度（或进出口截面 平均温度）。
5. 牛顿冷却公式中的平均温差
对恒热流条件，可取 (tw tf ) 作为 tm 。
对于恒壁温条件，截面上的局部温差是个变值，应利 用热平衡式：
hm Atm qmcp(tf tf )
外部流动：换热壁面上的流动边界层与热边界层能自由发 展，不会受到邻近壁面存在的限制。
一. 横掠单管换热
横掠单管：流体沿着 垂直于管子轴线的方 向流过管子表面。流 动具有边界层特征， 还会发生绕流脱体。
边界层的成长和脱体决了 外掠圆管换热的特征。
可采用以下分段幂次关联式：
Nu f C Re f n Prf 0.37
w )0.14
定性温度为流体平均温度tf （ w 按壁t温w
确定），管内径为特征长度，管子处于均匀壁
温。
实验验证范围为：Prf 0.48 ~ 16700,
0.0044(
f
)9.75
w
2.过渡流换热
推荐格尼林斯基提供的准则关联式
对于气体，0.6Prf 1.5;0.5Tf Tw 1.5;2300Re f 104
冷却流体时 n 0.3 。
式中: 定性温度采用流体平均温度 tf ，特征长度为
管内径。
实验验证范围： Ref 104 ~ 1.2 105, Prf 0.7 ~ 120, l / d 60。

第6章 单相流体对流换热及准则关联式

第6章 单相流体对流换热及准则关联式

根据质量守恒，掠过前半部时，
由于流动截面积逐渐缩小，流速
将逐渐增大，而到管子后半部，
由于流动截面逐渐增大，流速将 逐渐降低，大约以 = 90为界。
2013-7-9 15
3、横掠管束：
换热设备中管束的排列方式很多，比较普遍的 是顺排与叉排二种。
2013-7-9
16
流体掠过管束时，流动受到各排管子的连续干扰。来流 稳定，流经第一排后就产生扰动，以后又流过第二排、第三 排、扰动不断加强。叉排排列时更甚。在经过一定排数之后， 不管来流情况如何，流动都是很强烈的涡流 —— 达到管束 特有的稳定状态。
流动 起因 几何
形状 平壁： 自 由 流 动 换 热 竖壁 水平壁
流动 状态
层流 紊流 层流 紊流
准则方程式
Num C (Gr Pr)m
― P.165
式(6－16)
n
园管 (水平放 置)
式中：C、n值， 查P.166表6-5 (Gr.Pr)
29
2013-7-9
对 流 换 热 类 型 的 分 类 及 其 准 则 方 程 2013-7-9 式
4r 2 4f 2r d de 2r U
9
r1 r2
(5) 圆形管道：
d
2013-7-9
《注意》
把当量直径de作为定型尺寸，用同一公式进 行计算，并不是说明这二个现象相似。因为非 圆管与圆管，首先几何条件就不相似，而物理 现象的相似首先要满足几何相似的条件。
由于不是理论分析解而是实验解(经验公式)， 所以有误差。有误差存在，就有可能使二组不 相似现象的实验点落在同一个误差带范围内， 用同一个方程式来描写。 对于不同几何形状的物体能整理成一个经验 公式的话，说明几何形状的影响不大。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

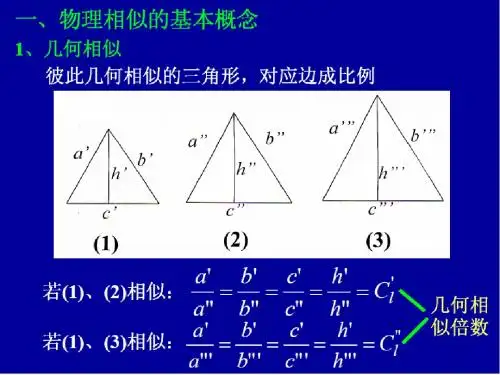
第6章复习题1、什么叫做两个现象相似，它们有什么共性？答：指那些用相同形式并具有相同内容的微分方程式所描述的现象，如果在相应的时刻与相应的地点上与现象有关的物理量一一对于成比例，则称为两个现象相似。

凡相似的现象，都有一个十分重要的特性，即描述该现象的同名特征数（准则）对应相等。

（1） 初始条件。

指非稳态问题中初始时刻的物理量分布。

（2） 边界条件。

所研究系统边界上的温度（或热六密度）、速度分布等条件。

（3） 几何条件。

换热表面的几何形状、位置、以及表面的粗糙度等。

（4） 物理条件。

物体的种类与物性。

2．试举出工程技术中应用相似原理的两个例子．3．当一个由若干个物理量所组成的试验数据转换成数目较少的无量纲以后，这个试验数据的性质起了什么变化？4．外掠单管与管内流动这两个流动现象在本质上有什么不同？5、对于外接管束的换热，整个管束的平均表面传热系数只有在流动方向管排数大于一定值后才与排数无关，试分析原因。

答：因后排管受到前排管尾流的影响（扰动）作用对平均表面传热系数的影响直到10排管子以上的管子才能消失。

6、试简述充分发展的管内流动与换热这一概念的含义。

答：由于流体由大空间进入管内时，管内形成的边界层由零开始发展直到管子的中心线位置，这种影响才不发生变法，同样在此时对流换热系数才不受局部对流换热系数的影响。

7、什么叫大空间自然对流换热？什么叫有限自然对流换热？这与强制对流中的外部流动和内部流动有什么异同？答：大空间作自然对流时，流体的冷却过程与加热过程互不影响，当其流动时形成的边界层相互干扰时，称为有限空间自然对流。

这与外部流动和内部流动的划分有类似的地方，但流动的动因不同，一个由外在因素引起的流动，一个是由流体的温度不同而引起的流动。

8．简述射流冲击传热时被冲击表面上局部表面传热系数的分布规律．9．简述数数，数，Gr Nu Pr 的物理意义．Bi Nu 数与数有什么区别？ 10．对于新遇到的一种对流传热现象，在从参考资料中寻找换热的特征数方程时要注意什么？相似原理与量纲分析6－1 、在一台缩小成为实物1/8的模型中，用200C 的空气来模拟实物中平均温度为2000C 空气的加热过程。

实物中空气的平均流速为6.03m/s ，问模型中的流速应为若干？若模型中的平均表面传热系数为195W/(m 2K)，求相应实物中的值。

在这一实物中，模型与实物中流体的Pr 数并不严格相等，你认为这样的模化试验有无实用价值？用价值的。

这样的模化试验是有实分相近数并不严格相等，但十型与流体的上述模化试验，虽然模得：又由：：时的物性参数为：和空气在应相等实物中的根据相似理论，模型与解：Pr )/(99.3659.293.381195))((/85.2003.6885.3406.15))((680.0Pr ,/1093.3,/1085.34200703.0Pr ,/1059.2,/1006.15C 2020020Re 212212212221122211222262121261K m W l l h h Nu Nu sm u l l u l u l u K m W s m C K m W s m C C l l l⋅=⨯⨯====⨯⨯==⇒==⋅⨯=⨯=︒=⋅⨯=⨯=︒︒︒----λλννννλνλν6－2、对于恒壁温边界条件的自然对流，试用量纲分析方法导出：Pr),(Gr f Nu =。

提示：在自然对流换热中t ga ∆起相当于强制对流中流速的作用。

[][][][][][][]11010111)()()(0)(347)(111112113311111121111131113113333322222111113211121233231===-==∆∆∆⇒=-=-∆+-+------++----------------a d c b L T M T L T L M T M L T M t g cL t g L t g hL r n L T ML T L ML LT M LT T M Lct g hd c b a d c b b c b d d c c c b b b a d c b a d c b a d c b a ，，，解得：＝展开：＝＝＝则各准内涵表达式如下＝，，解：θθθπαηλπαηλρπαηλππππφθθθηρλαPr)(Pr/)(03031313/)(22/322/121202/)(011033333333231333323233333333332123330102032222232222232212222222322223200111，即原则性准则方程：，，，得：各系数乘以，，，Gr f Nu c t g cL a d c b M T L T L T L M T L M L T L Gr tL g t g L a d c b T L M T L T L M T L M L ML NuhL t g hL c b d c b b d c b a d d c c c b b b b a d c b b d c b a c b d d c c c b b b b a ===∆====-=⇒===∆=∆===-==⇒====∆=-+------+-++-----------+-++-++-------ληαηλπθθθπνααηλρπθθπλαηλπ6－3、试用量纲分析法证明，恒壁温情况下导出的Pr),(Gr f Nu =的关系式对于恒热流边界条件也是合适的，只是此时Gr 数应定义为λνα24/ql g Gr =*。

证明：在习题18的分析中以q 代替t ∆（因为此时热流密度已知，而t ∆中的壁温为未知），则有),,,,,(1ρμλαp c l q g f h =，仍以l ,,,μρλ为基本变量，则有：λμρλαhlh l d c h =∏→=∏111111；()()()()()()()()()22222222222222222215513115113152L ααααααθθθαμρλ-----++++--+-------===∏c c h d c h d c h d c h T M LMT L T ML ML LMT q g l12-=∴α ，22-=c ，22=b ，42=d得*--===∏Gr ql g l q g 2442212λναμρλα； ()Pr ,33333、*=∴=∏→=∏Gr f Nu c c l pp dc h j λμμρλα。

6－4、已知：对于常物性流体横向掠过管束时的对流换热，当流动方向上的排数大于10时，试验发现，管束的平均表面传热系数h 取决于下列因素：流体速度u ；流体物性p c 、、、ληρ；几何参数21s s d 、、。

求：试用量纲分析法证明，此时的对流换热关系式可以整理为：()d s d s f Nu //Pr Re 21、、、= 解：基本物理量有 h 、u 、ρ、η、λ、p C 、d 、1s 、2s 、共九个，基本量纲有4个（时间T 、长度L 、质量M 、温度Q ），n=9，γ=7。

方程有五组，选取h d u ,,,λ为基本物理量，得：11111d c b a d hu ηλπ⨯⨯⨯=22222dc b ad u ηλρπ⨯⨯⨯=33333d c b a p d u c ηλπ⨯⨯⨯=444414d c b a d u s ηλπ⨯⨯⨯=555525dc b ad u s ηλπ⨯⨯⨯=31min --=T MQ h d L d d =min 11m i n --=T ML d η31min --=T MLQ d λ 1m i n -=LT u d111111111133111dc b ad c a c d c L T Q M -++------++=π22222222223312dc b ad c a c d c L T Q M -+++-----++=π 333333333323213d c b a d c a c d c L T Q M -+++------+=π 4444444444134d c b a d c a c d c L T Q M -+++----+=π 5555555555135d c b a d c a c d c L T Q M -+++----+=π上式等号左边为无量纲量，因此等号右边各量纲的指数必为零（量纲和谐原理），故得：⇒⎪⎪⎩⎪⎪⎨⎧=-++=----=--=++003301011111111111d c b a d c a c d c ⎪⎪⎩⎪⎪⎨⎧===-=10011111b a d c ⇒⎪⎪⎩⎪⎪⎨⎧=-+++-=---==++03030012222222222d c b a d c a c d c ⎪⎪⎩⎪⎪⎨⎧==-==11102222b a d c ⇒⎪⎪⎩⎪⎪⎨⎧=-+++=----=--=+020320103333333333d c b a d c a c d c ⎪⎪⎩⎪⎪⎨⎧===-=00113333b a d c ⇒⎪⎪⎩⎪⎪⎨⎧=-+++=---=-=+0103004444444444d c b a d c a c d c ⎪⎪⎩⎪⎪⎨⎧====00104444b a d c ⇒⎪⎪⎩⎪⎪⎨⎧=-+++=---=-=+0103005555555555d c b a d c a c d c ⎪⎪⎩⎪⎪⎨⎧-====10005555b a d c因而得：Nundd u h ==⋅⋅⋅⋅=-ληλπ01101Re/10112==⋅⋅⋅⋅=-ρηηλρπudd u Pr11003==⋅⋅⋅⋅=-ληηλπp p c d u c d sd u s 1001014=⋅⋅⋅⋅=-ηλπd s d u s 2001025=⋅⋅⋅⋅=-ηλπ因此 ).......(21s s c d u f h p ρηλ=的关系式可转化为：)..Pr .(Re 21d s d s f Nu =6－5、已知：有人曾经给出下列流体外掠正方形柱体（其一面与来流方向垂直）的换热数据：Nu Re Pr41 5000 2.2 125 20000 3.9 117 41000 0.7 202900000.7求：采用mnC Nu Pr Re =的关系式来整理数据并取m=1/3，试确定其中的常数C 与指数n 在上述Re 及Pr 的范围内，当方形柱体的截面对角线与来流方向平行时，可否用此式进行计算，为什么？解： 由mn C Nu Pr Re =有Pr lg Re lg lg lg m n C Nu ++=根据实验数据有： Re lg Pr lg 1lg 与m Nu -成线性关系Nu lg Re lg Pr lg 1m Prlg 31lg -Nu Re lg1.62 3.699 0.1141 1.5059 3.6992.0969 4.3010 0.1970 1.8999 4.301 2.0681 4.6128 -0.052 2.1201 4.6128 2.3054 4.9542 -0.052 2.3574 4.9542678.0699.39542.45059.13574.2=--=n C lg 为直线在纵坐标上的截距。