六年级数学下册-《比例问题》练习及答案

第四单元：比例第7课时：用比例解决问题班级：姓名: 等级:【基础训练】一、选择题1．甲有图书120本，乙有图书60本，甲给乙（）本后，乙的图书与甲的图书比是4∶5。

A．20 B．40 C．602．一块长方形的耕地（如图），已知其中三小块长方形的面积分别是15km2、16km2和20km2，则阴影部分的面积是（）km2A．19 B．12 C．11 D．213．一个玻璃瓶内原有一些盐水，盐与盐水的质量比为1∶12，加入15克盐后，盐与盐水的质量比为1∶9。

瓶内原有盐水（）克。

A．480 B．440 C．360 D．3004．如下图：一辆汽车早上8：00从A地出发，以平均每小时60千米的速度行驶，11：30到达目的地．目的地应该是（）．A．甲城B．乙城C．丙城5．下面的问题，还需要确定一个信息才能解决，是（）B．玫瑰、三种花总数的比是1：3C．三种花的数量是百合的6倍D．玫瑰的数量是百合的二、填空题6．一个三角形中三个内角的度数的比是2∶3∶7，它最大内角的度数是( )，这是一个( )三角形。

7．某小学五、六年级参加数学竞赛的人数比是8∶7，六年级获奖人数是五年级获奖人数的37，两个年级各有50名同学未获奖，六年级有( )名同学获奖。

8．甲、乙两人从武汉长江大桥的两端出发，相向而行，乙先走556.8米，然后甲从桥的另外一端开始出发。

已知甲、乙两人的速度是3∶2，甲、乙相遇时所走的路程是2∶3，问武汉长江大桥全长( )米。

9．已知平行四边形ABCD周长为80厘米，以BC为底时，高为21厘米．以CD为底时高为27厘米，那么平行四边形的面积为（）平方厘米．10．甲、乙、丙三人进行200米赛跑，当甲到达终点时，乙离终点还有20米，丙离终点还有25米，如果甲、乙、丙赛跑时的速度都不变，那么，当乙到达终点时，丙离终点还有( )米。

三、判断题11．时间和速度成反比例．( )12．变速自行车蹬同样的圈数时，前后轮齿数比的比值越大，自行车走得越远。

人教版六年级数学下册第四单元《比例》课后练习（共十练附答案）4.1 比例的意义1．判断两个比能否组成比例，并把组成的比例写出来，不能的说出理由。

（1）0.9︰1.2和8︰6（2） 0.22.5 和 450（3）6︰45和0.8︰6 （4）12︰1.2和1︰1102．写出比值是14的两个比： 和 ，组成的比例是 。

3．连一连。

（将两个能组成比例的比连起来）2︰3 0.5︰0.20.6︰0.8 13︰1103︰1.2 4︰623︰15 35︰454．在（ ）里填上适当的数。

（1）3︰（ ）= （ ）︰12（2）24︰9 = 8︰（ ）（3）（ ）︰3 = 8︰（ ）填完之后，将各组比例中的第一项与第四项相乘，第二项与第三项相乘，算一算，你有什么发现？4.2 比例的基本性质1．填一填。

（1）如果a ︰b ＝c ︰d ，那么，（ ）×（ ）＝（ ）×（ ）。

（b 、d 都不为0）（2）一个比例的两个内项分别是5和a ，则两个外项的积是（ ）。

2．应用比例的基本性质，判断下面哪组中的两个比可以组成比例。

（1）23 ︰ 14 和 45 ︰310（2）34 ︰1.2和 54︰1.63．根据等式，改写成比例式。

（1）14×12=21×8 （2）A ×B=C ×D4、用8，40，32再找上一个数组成比例，可以找哪些数？请写出组成的比例。

1．解比例。

（1）34 ︰56 ＝X ︰23 （2）1.5X ＝6122．根据下列条件列出比例，并解比例。

（1）8与X 的比等于13 与 56的比。

（2）什么数与314 的比值等于 79与1.2的比值？3．轮船模型是按照与实物大小1︰400的比例做成的，它的长是20.5cm ，这艘轮船的实际长多少米？4．下图是一个山坡的示意图，如果A 点的高度是40米，B 点的高度应是多少米？1.上表中，路程是随着 的变化而变化的， 和 是两种相关联的量，路程和时间的比值 ，也就是 和 成正比例关系，和 是成 的量。

比例的应用【运用比例解决问题】(2019﹒天河区模拟）晴晴全家“五一”到中山公园游玩，拍了许多照片，她买了一本相册，如果每页放6张照片，刚好放16页，现在晴晴打算每页只放4张，25页够放下这些照片吗？（用比例解）【考点】比例的应用．用比例解决问题【分析】根据照片的数量是一定的，每页放相片的张数×放照片的页数＝照片的数量（一定），由此判断每页放相片的张数与放照片的页数成反比例，设出未知数，列出比例解答即可．【解答】解：设每页只放4张，可以放x 页，4x ＝6×16,x ＝6×164, x ＝24，因为25＞24,所以25页够放下这些照片，答：25页够放下这些照片．【点评】解答此题的关键是，根据题意，先判断哪两种相关联的量成何比例，即两个量的乘积一定则成反比例，两个量的比值一定则成正比例；再列出比例解答即可．例2 (2019春﹒法库县期末）淘气和笑笑收集的邮票张数的比是3：5．淘气收集了36张邮票，笑笑收集了多少张邮票？【用比例解】【考点】比例的应用．比例的应用【专题】比和比例应用题．【分析】已知淘气和笑笑收集的邮票张数的比是3：5．淘气收集了36张邮票，设笑笑收集了x 张邮票，据此列比例解答．【解答】解：设笑笑收集了x 张邮票，3：5＝36：x3x ＝5×36x ＝5×363x ＝60．答：笑笑收集了60张邮票．【点评】此题考查的目的是理解掌握比例的意义、比例的基本性质及应用．例3 一辆汽车从甲地开往乙地，每小时行70千米，5小时到达。

如果要4小时到达，每小时要行多少千米？（1）这道题里的路程是一定的，________和________成_______比例。

所以两次行驶的________和________的________________是相等的。

（2）如果设每小时需要行驶X 千米答：每小时需要行驶 千米。

(3)如果把例2中的第三个已知条件和问题互换一下：一辆汽车从甲地开往乙地，每小时行70千米，5小时到达。

六年级数学下册《用比例解决问题》练习题及答案解析学校:___________姓名：___________班级：_____________一、选择题1．一条2厘米的线段，选用下面比例尺（）画出的平面图最大。

A．1∶200B．1∶5000C．1∶1D．2∶12．老师买了同样数目的田格本、横线本和练习本。

他发给每个同学1个田格本、3个横线本和5个练习本。

这时横线本还剩24个，那么田格本和练习本共剩了（）个。

A．48B．50C．54D．563．把一个圆柱削成一个最大的圆锥，削去的体积是48立方分米，圆柱的体积是（）立方分米。

A．144B．24C．724．一幅地图的比例尺是1∶1000000，下列说法不正确的是（）。

A．这是一个数值比例尺B．说明要把实际距离缩小为11000000后，再画在图纸上C．图上距离相当于实际距离的1 1000000D．图上1厘米相当于实际1000000米5．下列各数中，（）不能与2、8、10组成比例。

A．58B．85C．52D．406．甲乙两个容积相同的瓶子分别装满盐水，已知甲瓶中盐、水的比是2∶3，乙瓶中盐、水的比是3∶5，现在把甲、乙两瓶水混合在一起，则混合盐水中，盐与盐水的比是（）。

A．519B．521C．524D．31807．一个水池有甲乙两个水管。

单独开甲管，2小时可以把空池注满；单独开乙管，3小时可以把空池注满。

如果同时打开甲乙两管，（）小时可以把空池注满。

A．1B．15C．115D．58．希望小学合唱队共有队员108人，则（）一定不是男队员和女队员人数的比。

A．5∶4B．7∶5C．8∶7D．19∶17 9．表示x和y成正比例关系的式子是()．A．x＋y＝9B．y＝1.5x C．＝0D．xy＋1＝510．学校把560棵树的种植任务，按照六年级三个班的人数分配给各班。

一班有47人，二班有45人，三班有48人。

二班应种树（）。

A．192棵B．188棵C．180棵11．在一幅地图上，用20厘米的线段表示50千米的实际距离，那么这幅地图的比例尺是（）。

每日一练 六下第4单元4-4课时《解比例》班级 姓名一、 基础练习1.解比例。

2、 0.3：34 错误!未定义书签。

=2÷（ ）=（ ）：（ ）=（ ）10 =（ ）%3、学校合唱组男生与女生人数的比是3:4，合唱组男生有24人，女生有多少人？（你会用不同的方法解答吗？）二、 拓展练习1、解比例X ：34 =56 3:5=（X+6）：20 1.6:2.4=Y 4.52、选择（1）一杯牛奶，牛奶与水的比是1:6，喝掉一半后，牛奶与水的比是（ ）A.1:6B.1:3C.1:12D.6:1（2）不能与3、6、9组成比例的数是（ ）。

A.2B.12C.18D. 92（3）如果54:a 和152:b 能组成比例，那么，（ ）。

A.b a 32=B.b a 6=C.a b 32= D.b=6a （4）甲年龄的34 等于乙年龄的23，那么甲、乙的年龄比是（ ） A. 34 :23 B.9:8 C.8:9 D. 23 :343、填空1.两个圆的直径比是5:3，大圆的周长是15.7厘米，小圆的周长是（ ）厘米。

2.一个比例中，两个外项都是15，两个比的比值都是20，这个比例是（ ）3. 5、3、0.6和a 可以组成一个比例，a 可以是（ ），可以是（ ），还可以是（ ）三、 强化巩固★一个长5厘米、宽3厘米的长方形按4:1的比放大，得到的图形的周长是（ ）厘米，面积是（ ）平方厘米。

★比例5:3＝15:9的内项3增加6，要使比例成立，外项9应该增加（ ）。

★3X-4Y=0，那么X:Y=（ ）；如果a 3=b 15 ,那么a:b=（ ） ★★如果n m 5243=（m 、n 都不等于0），那么m ：n=（ ）：（ ），=mn （ ）。

四、 解决实际问题（运用比例的基本性质解答）1、 两杯水，第一杯加了20克糖，糖水共重170克。

第二杯水重210克，按照第一杯糖水中糖和水的质量比计算，第二杯水中要加入多少克糖？2、果园里种植苹果树棵树的23 和桃树棵树的34 相等，已知苹果树和桃树一共有340棵。

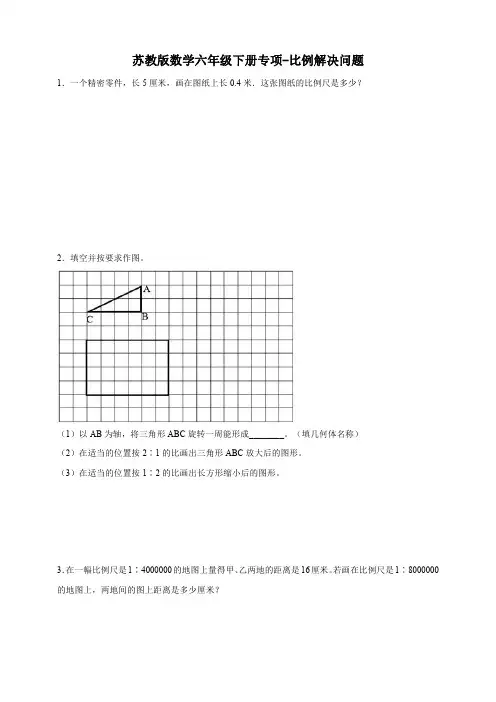
苏教版数学六年级下册专项-比例解决问题1．一个精密零件，长5厘米，画在图纸上长0.4米．这张图纸的比例尺是多少？2．填空并按要求作图。

（1）以AB为轴，将三角形ABC旋转一周能形成________。

（填几何体名称）（2）在适当的位置按2∶1的比画出三角形ABC放大后的图形。

（3）在适当的位置按1∶2的比画出长方形缩小后的图形。

3．在一幅比例尺是1∶4000000的地图上量得甲、乙两地的距离是16厘米。

若画在比例尺是1∶8000000的地图上，两地间的图上距离是多少厘米？4．画一画，填一填。

（1）按3∶1的比画出图形A放大后得到的图形B。

（2）按1∶2的比画出图形B缩小后得到的图形C。

我发现：放大或缩小前后的图形（）变了，但（）没有变，而且图形各部分长度是按一定的比变化的。

5．在一张比例尺是1∶150的建筑图纸上，量得一座大楼的长是6分米，这座大楼的实际长与宽的比是3∶1，这座大楼的实际宽是多少米？6．下图中小平行四边形按比放大后得到大平行四边形，求大平行四边形的高。

（单位：分米）12．根据图中提供的信息，完成下列问题。

（1）自来水厂要从水库取水，取水管道怎样铺最短，请在图中画出来。

（2）自来水厂到城区的送水管道经测算最短是2000米，请你测算：自来水厂到水库的取水管道最短需多少米？13．在一幅地图上，用5厘米长的线段表示实际距离100千米，这幅地图的比例尺是多少？如果甲市至乙市的铁路线路长150千米，那么这段铁路线路在这幅地图上的长度是多少厘米？14．江苏省云龙湖景区杏花坞广场是人们夏天避暑纳凉的佳处。

广场绿地面积与铺装面积的比是6∶5，其中铺装面积共5000平方米，绿地面积有多少平方米？15．甲乙两城相距150千米，在一幅地图上量得甲乙两城之间的距离是5厘米，同时在这幅地图上量得乙丙两城之间的距离是8厘米。

乙丙两城之间的实际距离是多少千米？20．下图中A点是游乐场所在的位置，B点是电影院所在的位置，两地实际距离相距2千米。

人教版六年级下册数学用正比例解决问题一.解比例。

51＝25x x 2＝5.311.2 32＝15x x 5.2＝4.01二、填空1.车轮直径一定，所行的路程和车轮的转数成（ ）比例。

2.因为每度电的价格一定，所以电费和用电的度数成（ ）比例。

3. 把下面的数量关系式补充完整路程÷（ ）＝时间 路程÷（ ）＝速度总价÷（ ）＝数量 总价÷ （ ）＝单价 三、判断1.两种相关联的量，不成正比例，就成反比例。

（ ）2.图上距离和实际距离成正比例。

（ ）3.X 和Y 表示两种变化的相关联的量，同时5X －7Y ＝0，X 和Y 不成比例。

（ ）4.分数的大小一定，它的分子和分母成正比例。

（ ）5.在一定的距离内，车轮周长和它转动的圈数成反比例。

（ ） 四、解决问题 1.2.小明买9本练习本花了4.5元，如果买同样的练习本20本需要付多少元？3.小明买9本练习本花了4.5元，如果用20元钱买同样的练习本，可以买多少本？4.运一批煤，18次运了90吨，照这样计算，14次可以运多少吨？5.运一批煤，18次运了90吨，照这样计算，多少次才能运完140吨煤？6.用8辆卡车每天可运货128吨，照这样计算，用同样的卡车11辆，每天可运货多少吨？7.一种水管，40米重60千克。

现称得一捆水管重270千克，这捆水管共长多少米？8.华南服装厂3天加工西装180套，照这样计算，要生产540套西装，需要多少天？9.王师傅生产25个零件需要1.5小时，照这样计算，生产125个零件需要多少小时？10.把一根3m长的标杆直立在地上，测得影长2.7m，同时测得旁边一棵树的影长比标杆影长多3.6m，这棵树高多少米？11.一辆汽车2小时行驶140千米，照这样的速度，从甲地到乙地的距离是400千米，需要行驶多少小时？12.一个修路队，原计划每天修400m,15天可以修完。

结果12天就完成任务，实际每天修多少米？参考答案：人教版六年级下册数学用正比例解决问题一.解比例。

六年级比例练习题带答案1. 题目：小明拥有5本英语书和3本数学书，求其英语书与数学书的比例。

解答：英语书与数学书的数量比为5:3，即英语书数 ÷数学书数 = 5 ÷ 3。

约分后得到英语书与数学书的比值为5:3。

2. 题目：某班级有60名男生和40名女生，请问男生和女生的比例是多少？解答：男生与女生的数量比为60:40，即男生数 ÷女生数 = 60 ÷ 40。

约分后得到男生和女生的比值为3:2。

3. 题目：一辆汽车经过一段路程用时6小时，如果速度提高一倍，则经过同样路程需要多少时间？解答：原速度为1单位路程/1小时，提高一倍后速度为2单位路程/1小时。

根据比例关系，原用时 ÷提高后用时 = 原速度 ÷提高后速度。

代入数值计算得到 6 ÷ x = 1 ÷ 2，求得 x = 12。

因此，提高后的速度下经过同样路程需要12小时。

4. 题目：在一家商店中，某商品售价为100元，若商家打八折出售，求打折后的售价。

解答：打八折意味着商品售价的80%，即打折后售价 = 商品售价 ×打折比例 = 100 × 80% = 80元。

5. 题目：某商品原价为120元，经过折扣出售后，售价为96元，求折扣比例。

解答：折扣比例 = 折扣金额 ÷商品原价 = (商品原价 - 折后售价) ÷商品原价 = (120 - 96) ÷ 120 = 24 ÷ 120 = 0.2。

因此，折扣比例为20%。

6. 题目：甲、乙两人分别走了12公里和15公里的路程，求他们的路程比。

解答：甲、乙两人的路程比为12:15，即甲走的路程 ÷乙走的路程= 12 ÷ 15。

约分后得到甲、乙两人的路程比为4:5。

7. 题目：一桶油漆可以涂刷80平方米的墙面，求涂刷100平方米墙面需要多少桶油漆？解答：1桶油漆可以涂刷80平方米的墙面，因此涂刷100平方米墙面需要的油漆桶数为 100 ÷ 80 = 1.25（桶）。

六年级下册数学《比例》易错题含答案一、填空1.4：5=24÷（ 30 ）； 3.5：（ 4.9 ）=5:7。

2.图上距离3厘米表示实际距离180千米，这幅图的比例尺是（ 1:6000000）。

3.如果x÷y=320×2，那么x和y成（正）比例；如果x:3=6:y，那么x和y成（反）比例。

4.一本书的总页数一定，看的天数与平均每天看的页数成（反）比例，总路程一定，已行的路程与未行的路程（不成）比例，长方体的体积一定，底面积和高成（反）比例。

5.小正方形和大正方形边长的比是4:5，小正方形和大正方形面积的比是( 16:25 )。

6.在一个比例中，两个内项的积是5.6，如果一个外项是2.8，另一个外项是（2 ）。

7.A×B=C，当C一定时，A和B成（反）比例；当B一定时，A与C成（正）比例。

8. 甲数/乙数=3/5，乙数比甲数多（40%）。

（填百分数）二、判断。

(对的画“√”，错的画“×”)1．数值比例尺都是写成前项是1的比。

( × )2．被除数一定，商和除数成正比例。

( × )3．六年级男生和女生的比是5:3，则女生比男生少52。

( √ )5．在比例中，两个外项是互质数，那么两个内项也一定是互质数。

( × )6.26只小鸟飞进5个笼子里，有一个笼子里至少飞进5只小鸟。

( × )三、解比例96：x=16：5解答：16x=96×5 ；16x÷16=96×5÷16；x=300.6：4.8=12：x解答：0.6x=4.8×12；0.6x÷0.6=57.6÷0.6；x=961.25：0.25=x：1.6解答：0.25x=1.25×1.6；0.25x÷0.25=2÷0.25；x=8四、解决问题1.修一条路，如果每天修120米，8天可以修完；如果每天修150米，几天可以修完？（用比例方法解）解：设x天可以修完；120×8=150x；150x=960；x=6.4答：6.4天可以修完。

第1课时比例的意义1.算一算下面哪两幅图片的长和宽的比值是相同的。

2.下面各组的两个比能组成比例吗?如果能,在括号里画“ ”。

6∶8和9∶12( ) 1.2∶0.6和38∶34( ) 56∶57和7∶6( ) 3.用右图中的4个数据可以组成多少个比例?答案:1.2.4∶1.8=2∶1.5 第一幅图和第二幅图是相同的。

2.( )( )( )3.解答:一共可以组成8个比例,分别是6∶3=8∶4 3∶6=4∶8 6∶8=3∶4 8∶6=4∶3 8∶4=6∶3 4∶8=3∶63∶4=6∶84∶3=8∶6第2课时比例的基本性质1.在比例9∶6=12∶8中,两个内项分别是( )和( ),两个外项分别是( )和( )。

把这个比例写成乘法等式为( )。

2.根据比例的基本性质,在括号里填上合适的数。

1.2∶67=2.4∶( ) 58=( )243∶9=( )∶1514( )=73 ( )∶3=4∶( )0.5∶( )=( )∶123.判断:12∶13=64是比,而不是比例。

答案:1.6 12 9 8 6×12=9×82.127 15 5 6 后两题答案不唯一,如:2 6 2 33.错解分析:错误解答错在只把64看作了比值,没有理解比例的含义。

64既可以看作比值,也可以看作6与4的比。

如果64看作6与4的比,那么12∶13与6∶4能组成比例,因此,12∶13=64可以看作是比,也可以看作是比例。

正确解答:✕第3课时解比例1.在下面的括号里填上合适的数。

8∶2=24∶( )( )15=451.5∶3=( )∶34 48∶( )=3.6∶92.解比例。

0.7∶x =48∶4858∶5=24∶x67∶56=65∶x 56∶14=x ∶23 3.按照下面的条件列出比例,然后解比例。

(1)6与5的比等于30与x 的比。

(2)等号左边的比是2∶1.5,等号右边的比的前项和后项分别是6和x 。

答案:1.6 12 17 1202.x=750 x=15 x=76 x=2093.(1)6∶5=30∶x x=25(2)2∶1.5=6∶x x=4.5第4课时练习课1.照这样计算,小雪15分钟行多少米?2.某美术组男生与女生的人数比是6∶7,男生有12人,女生有多少人?3.一幅画,长与宽的比是3∶2,已知这幅画的宽是80厘米,这幅画的长是多少厘米?答案:1.解:设小雪15分钟行x米。