当前位置：文档之家 › 二次根式第一课时-史春雷(1)

二次根式第一课时-史春雷(1)

  • 格式：ppt
  • 大小：520.50 KB
  • 文档页数：23

下载文档原格式

  / 23

合集下载

16.1二次根式第1课时课件

16.1二次根式第1课时课件

呢?
5
形如 a (a≥0)的式子叫做二次根式
(1)表示a的算术平方根; (2)a可以是数,也可以是代数式; (3)从形式上看,含有二次根号; (4)a≥0, a ≥0.
例：下列各式中,哪些是二次根式?并指出二 次根式中的被开方数.
7, 22 , 4 10, x 3(x 3), y 1 y 1, x 12 , x2 3, y xy 0
解:由a+1≥0,得a≥-1. ∴字母a的取值范围是大于或等于-1的实数.
2 1
1 2a
解:由
1 1 2a
>0,得1-2a>0,即a
<
1 2
∴字母a的取值
范围是小于
1 2
的实数.
3 a - 32
解:因为无论a取何值,都有(a-3)2≥0,所以字母a 的取值范围是全体实数.
4 a 1
解:因为无论a取何值,都有|a|+1>0,所以字母a的 取值范围是全体实数.
在分母上,因此 2x 1 解得x > 1 .故选C.
≠0.则22xx
1 1
0， 0.
2
3.当x= -3 时,二次根式 x + 3 有最小
值,其最小值是 0 .
解析: ∵二次根式有意义,∴x+3≥0,即x+3 的最小值是0,∴x+3=0,解得x=-3.
4.求下列各式中字母a的取值范围: 1 a +1
x
解: 7，x-3 x 3， x 12， y (xy＞0)
x y
是二次根式.其中被开方数依次是7,x-3,(x+1)2，x .
[解题策略] ①当被开方数形式是含有字母的代数式时, 可以把这个代数式看成一个整体.如 x2 2015 的被开方数是 x2 2015.

八年级下册数学课件(鲁教版)二次根式的性质 第一课时

八年级下册数学课件(鲁教版)二次根式的性质 第一课时
利用上面的性质可以计 算、化简一些二次根式.
例题引领
例1（1Βιβλιοθήκη 36（2） 9 43
0.5
4
a
x2
2
6 20
=
6 20
ab a b（a≥0，b≥0） 利用它可以对二次根式进行化简.
（2） 27
（3） 4a2
65 10 7
12 15x4y3
小试牛刀
化简:
(1) 12 (2) 27 15
明确目标
1.理解掌握a2的算术平方根公式 ( a )2 a （a≥0），并会利用它进行计算和化简. 2.理解积的算术平方根 ab= ·a （ba≥0，b≥0） 并利用它进行计算和化简.
知识铺垫
1. 形如 （aa≥0）的式子叫做二次根式．
其中a为整式或分式，a叫做被开方式．
特点：①都是形如 a 的式子，
②a都是非负数.
2.因为 a (a ≥ 0)表示a的算术平方根，所以 a ≥ 0(a ≥ 0)；
( a )2 a(a≥ 0); a ( a )2 (a≥ 0).
(1)计算 22 , 32 , 1 2 , 02的值,你发现了什么? 2
(2)当a ≥ 0时, a2的算术平方根是多少?由此你能得到 一个怎样的等式? 当a ≥ 0时, a2 a.
(3) 4a3
化简二次根式，就要把被开方数 中的平方数（或平方式）从根号里 开出来.
1. 当a ≥ 0时, a2 a.
2. 当a ≥ 0时, ( a )2 a2 .
3.

苏教版二次根式教案第一课时

苏教版二次根式教案第一课时

苏教版二次根式教案第一课时教案标题：苏教版二次根式教案第一课时教学目标：1. 理解二次根式的概念和性质。

2. 掌握二次根式的化简和运算方法。

3. 能够应用二次根式解决实际问题。

教学准备：1. 教材：苏教版二次根式教材。

2. 教具：黑板、粉笔、教学PPT等。

3. 学具：练习册、作业本等。

教学步骤：Step 1：导入新知1. 引导学生回顾一元二次方程的知识，通过问题引入二次根式的概念。

2. 提问：“什么是二次根式？二次根式有哪些特点？”引导学生思考并回答。

Step 2：概念解释与讲解1. 通过教学PPT或板书，对二次根式的定义进行解释，并给出示例。

2. 讲解二次根式的基本性质，如二次根式的分子中不含有平方根、二次根式的和差化简等。

Step 3：化简与运算1. 引导学生通过例题掌握化简二次根式的方法，如合并同类项、有理化分母等。

2. 通过练习题让学生巩固化简二次根式的基本技巧。

3. 引导学生通过例题和练习题掌握二次根式的加减乘除运算方法。

Step 4：应用解决实际问题1. 设计一些与实际生活相关的问题，引导学生运用二次根式解决问题。

2. 分组讨论和展示解题过程，加深学生对二次根式应用的理解。

Step 5：小结与作业布置1. 对本节课所学内容进行小结，强调二次根式的概念、性质和运算方法。

2. 布置相应的课后作业，巩固所学知识。

教学延伸：1. 对于学习较快的学生，可以提供更多的挑战性练习，如复杂的二次根式运算或解决实际问题。

2. 对于学习较慢的学生，可以提供更多的练习机会，加强基本技能的训练。

教学反思：本节课通过引入问题、概念解释、化简与运算、应用解决实际问题等环节，全面培养学生对二次根式的理解和应用能力。

在教学过程中，教师要注重激发学生的学习兴趣，提高课堂互动，使学生能够主动思考和解决问题。

同时，教师还要根据学生的实际情况进行差异化教学，确保每个学生都能够达到预期的学习目标。

16.1二次根式(一)

16.1二次根式(一)
系，体会研究二次根式的必要性.
培养学生合作交流的意识.
为概括二次根式的概念作铺垫。
体验数学在生活中应用的广泛性.
检测学生对知识的掌握情况及应用能力，初步体验成功的喜悦。
进一步加深学生对二次根式被开方数必须是非负数的理解．培养学生科学严谨的学习态度。
学情分析
八年级的学生大约在13岁左右，有一定的学习经验和生活经验，知道并会求一个数的平方，这些是学习本节课的知识基础。基于学生的学习基础，在研究的方法和合情推理方面还存在欠缺．他们经历一些探究的过程：动手实践、观察猜想、归纳总结、巩固应用等．因此，本节课的学习，可以引导学生通过探究研究方法．八年级的学生观察、操作、猜想能力较强，但归纳、运用数学意识的思想比较薄弱，需要在课堂教学中进一步加强引导。根据学生的认知特点和接受水平，本节课把学生掌握知识作为教学的主线，同时也为学习下节课的内容打好坚实的基础。
（2）一个长方形围栏，长是宽的2倍，面积为130m?，则它的宽为______m．
（3）一个物体从高处自由落下，落到地面所用的时间t（单位：s）与开始落下的高度h（单位：m）满足关系h=5t?，如果用含有h的式子表示t，则t=_____．
问题2：上面得到的式子 ， ， 分别表示什么意义？它们有什么共同特征？
A. B. C. D.
2.当 时，二次根式 无意义．
3.当 时，二次根式 有最小值，其最小值是．
4.对于 ，小红根据被开方数是非负数，得 出的取值范围是 ≥ ．小慧认为还应考虑分母不为0的情况．你认为小慧的想法正确吗？试求出 的取值范围．
（2）4的算术平方根为2，用式子表示为 =__________；正数a的算术平方根为_______， 0的算术平方根为_______；式子 的意义是。

八年级数学下册教学课件《二次根式》(第1课时)

八年级数学下册教学课件《二次根式》(第1课时)
(3)多个二次根式相加如
A B ... N
A≥0；
B≥0；


...
N≥0；
(4)二次根式与分式的和如
A≥0且B≠0.
B
有意义的条件：A＞0；
A
A
有意义的条件：
1
有意义的条件：
B
巩固练习
16.1 二次根式
x取何值时,下列二次根式有意义?
（1）
x 1
（2）
x≥1
（4）
3.若 x 2 在实数范围内有意义，则x的取值范围在数轴上
表示正确的是（ D ）
A．
B．
C．
D．
课堂检测
16.1 二次根式
基 础 巩 固 题
1.下面的式子是二次根式的是( A )
A. a 1
2
B. 3
33
C. -1
1
D. a
2
2.二次根式 2 x 4 中的x的取值范围是（ D ）
A．x＜﹣2
(7)
1
x
3x
x≤0
（5）
x3
x>0
x≥0
（3） 4x 2
x为全体实数
（6） 1
x 2 x≠0
x 1
( x 2)0 (8)
x3
x2
（9）
x
x≥-1且x≠2
x>0
x 1
2
x为全体实数
探究新知
16.1 二次根式
知识点 2
【回顾思考】二次根式
二次根式的双重非负性
a 的被开方数a的取值范围是什么？它
人教版 数学 八年级 下册
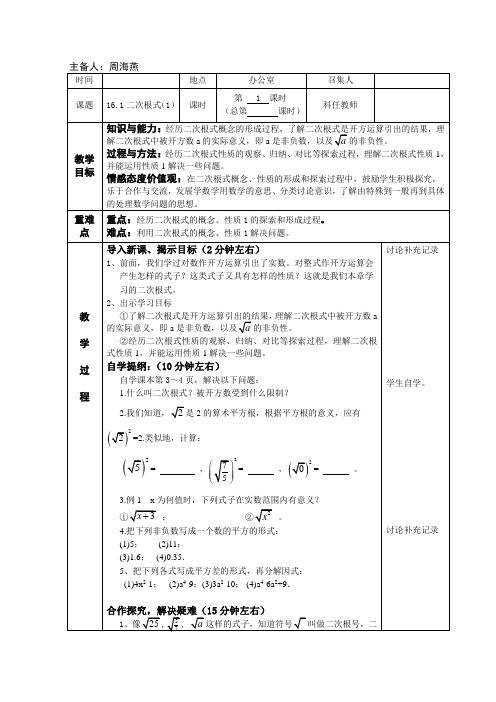
16.1 二次根式
16.1 二次根式（第1课时）

二次根式(1)

二次根式(1)
(3)1.6；(4)0.35．
5、把下列各式写成平方差的形式，再分解因式：
(1)4x2-1；(2)a4-9；(3)3a2-10；(4)a4-6a2+9．
合作探究，解决疑难（15分钟左右）
1、像 , , 这样的式子，知道符号 叫做二次根号，二次根号下的数叫做被开方数。因为在实数范围内，负数没有平方根，所以被开方数只能是正数或零。也就是说当a≥0时， 是有意义的，它表示a的算术平方根。
情感态度价值观：在二次根式概念、性质的形成和探索过程中，鼓励学生积极探究，乐于合作与交流，发展学数学用数学的意思、分类讨论意识，了解由特殊到一般再到具体的处理数学问题的思想。
重难点
重点：经历二次根式的概念、性质1的探索和形成过程。
难点：利用二次根式的概念、性质1解决问题。
教
学
过
程
教
学
过
程
导入新课、揭示目标（2分钟左右）
3、二次根式的性质1；
布置作业，拓展延伸（8分钟）
课堂作业：
必做题:习题16.1第2,4题。
选做题:习题16.1第7题。
课外作业:习题16.1第1、3题。
讨论补充记录
学生自学。
讨论补充记录
板书
设计
一、复习引入四、课堂小结：
二、自主学习五、当堂训练
三、合作探究六、布置作业
教学反思
定义：形式如 （a≥0）式子叫做二次根式。
2、性质1 =a (a≥0)。
反之，也成立。即a= (a≥0)。
3、例1。
4、例2。
5、例3。
巩固新知，当堂训练（8分钟）
课堂小结（2分钟）
一路下来，我们结识了很多新知识，你能谈谈自己的收获吗？说一说，让大家一起来分享。

二次根式第一课时课堂实录

2.7二次根式 第一课时一. 教学目标1.认识二次根式和最简二次根式的概念，并能用二次根式的性质进行化简。

2.用类比的方法，引入二次根式的性质、公式。

3.通过二次根式的化简，培养学生抓住问题的关键来解决问题的基本思路。

二．教学重难点正确运用公式b a b a ∙=⋅（a ≥0，b ≥0），b ab a=（a ≥0， b ＞0）并能进行熟练地运算，理解法则中b a b a ∙=⋅（a ≥0，b ≥0），b aba=（a ≥0， b ＞0）a 、b各满足什么条件。

三．新旧只是连接运用二次根式是在平方根，立方根，实数的基础上，进一步研究二次根式的概念和性质。

与已学内容实数，整式和勾股定理联系紧密，同时也是以后将要学习的锐角三角函数，一元二次方程和二次函数等内容的重要基础。

本课时研究的内容是下一课时二次根式的运算的基础和依据。

做一做：填空：（1）94⨯94⨯2516⨯2516⨯＝，94＝；9425162516＝，＝；＝，＝；＝，＝．66202023234545有何发现：49⨯＝1625⨯＝49＝1625＝49⨯，1625⨯，49，1625．＝，6.48067⨯76⨯＝；76（2）用计算器计算：＝，＝．6.4800.92550.9255有何发现：6776⨯7649⨯＝，49⨯1625⨯＝，1625⨯49＝，491625＝．1625观察上面的结果你可得出什么规律？＝67⨯，＝67．知识巩固•例1 化简•（1）；•（2）；•（3）。

教师首先讲解第一个例题。

师：【根号下是81乘以64，我们应用第一个公式，就等于728964816481=⨯=⨯=⨯】教师要注意格式。

师：【就是这样简单的应用我们的公式，下面两个题同学们在课堂本上写，我找两个同学来做。

】 学生能很快地写出正确答案。

学生得出答案.35.....65.....72. 师：【我们为什么要学习二次根式的性质呢？是想去化简二化简下面的二次根式.化简：4527319816125。

内蒙古乌兰浩特市第十二中学八年级数学人教版下册教案16.1 二次根式(第一课时)

教学重难点
重点： 有意义的条件. 2. ≥0时 ≥0的应用. 3. 和 的运算、化简。
难点： <0时 的化简.
教学方法与手段
方法：引导启发手段：多媒体
教
学
过
程
教学内容
教师活动
学生活动
一、复习引入
用带有根号的式子填空，看看写出的结果有什么特点：
（1）要做一个两条直角边的长分别是7cm和4cm的三角尺，斜边的长应为_________________cm
16.1二次根式
问题1例1例3
问题2例2例4
问题3
教学反思
参考资料
（学生活动）议一议：
1．-1有算术平方根吗？
2．0的算术平方根是多少？
3．当a<0， 有意义吗？
例2解：由3x-1≥0，得：x≥
当x≥ 时， 在实数范围内有意义．
本节课要掌握：
1．形如 （a≥0）的式子叫做二次根式，“ ”称为二次根号．
2Hale Waihona Puke 要使二次根式在实数范围内有意义，必须满足被开方数是非负数．
板书设计
分析例题1：二次根式应满足两个条件：第一，有二次根号“ ”；第二，被开方数是正数或0．
分析例题2：由二次根式的定义可知，被开方数一定要大于或等于0，所以3x-1≥0， 才能有意义．
分析：要使 + 在实数范围内有意义，必须同时满足 中的≥0和 中的x+1≠0．
（学生活动）请同学们独立完成下列三个问题。
教案号
1
主备教师
斯琴花
授课时间
2月24日
课题
16．1二次根式(1)
课标要求
教学目标
1知识与技能：通过探究知道二次根式定义，掌握二次根式中字母的取值范围。

21.1二次根式(第1课时)

两个非负数的和为0，则这两
必做题
1.教材P5习题21.1
2.复习巩固1题2题(1)、(2)
4题(1)、(2)
选做题
配套练习P2. 9题
配套练习P1. 8题、
配套练习P3. 12题
教师布置作业，动员分层要求。
学生按要求课外完成
教
后
反
思
【当堂达标自测题】
一、填空题
1.16的平方根是.
（5）当x-y≥0时是二次根式,当x-y<0时不是二次根式；即当x≥y是二次根式,当x<y时不是二次根式.
2.教材第3页
练习1、2、3.
3.计算：
（1）
（1）、（2）小题学生口答。
（3）小题请学生认真思考后回答；
（4）（5）两小题需要分情况讨论，学生思考、交流.
教师可提示、点拨.
教材第3页练习
学生分小组交流合作完成，师巡视辅导有困难的学生.
2．已知一个正数的平方根是 和 ，则这个数是．
3．函数 自变量 的取值范围是．
4．当x=________时，二次根式 有意义．
二、选择题
5．下列各式中是二次根式的是（）
A B C D
6．若使已知 为实数，那么 等于（）
A. B. C.－1 D. 0
7．二次根式 在实数范围内有意义，则x的取值范围是
A． B． C． D．
教师提出问题（2），检查学生对所学知识的掌握情况，并引导学生将所学知识与新知识相联系。
教师提出问题（3）学生总结二次根式的概念，思考 中a≥0的作用和原因
教师出示例题，提问：二次根式有意义的条件是什么？
学生口答，独立完成例1.
师强调解体格式
师提问：x的取值范围与x的指数有什么关系？

吉林省伊通县实验中学九年级数学上册《21.1 二次根式

《21.1 二次根式》教案（第1课时）
教学目标：
知识技能：使学生理解并掌握二次根式的概念，掌握二次根式中被开方数的取值范围和二次根式的取值范围.
教学方法：启发式教学
教学手段：多媒体教学
教学准备：多媒体课件
课时：1课时
教学过程：
问题与情境
活动一回顾与思考
1．４的平方根是_____；0的平方根是______；－16的平方根是____.
2．5的平方根是_______；5的算术平方根是____.
3．直角三角形的两条直角边分别为7和4，斜边为__.
4．正方形的面积为s,则它的边长为_____.
活动二接触新知
上面3、4题的结果是，
他们表示一些正数的算术平方根.
1.二次根式的定义:一般的,我们把形如(≥0)的式子叫做二次根式，“” 称为二次根号.
2.例题与练习
例1.下列各式是否为二次根式?
（1）;（2）（3）;（4）;（5）.
（5）当x-y≥0时是二次根式,当x-y<0时不是二次根式；即当x≥y是二次根式,当x<y时不是二次根式.
当x≤时，在实数范围内有意义；
（3）由-5x≥0,得x≤0;
当x≤0时，在实数范围内有意义；
（4）∵≥0，
∴+1>0，
∴x为任意实数都有意义.
练习:
1. 一个矩形的面积是18cm2,它的边长之比为2:3,它的边长应为多少？
2.当是怎样的实数时，下列各式在实数范围内有意义？
教学后记：。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

( a)
a
2
2
读作： 的算术平方根的平方 的算术平方根的平方. 读作：a的算术平方根的平方 读作： 的平方的算术平方根 的平方的算术平方根. 读作：a的平方的算术平方根
（3）取值范围不同 ）
( a)
2
= a（a ≥ 0）中，必必必必a ≥ 0，即a是一个非负数.
a 2 = a 中， a可取一可实数
（4）意义不同，运算顺序也不同 ）意义不同，运算顺序也不同.
2 2
( )
2
（3） 0.3 (5) −
; .
(−π)
=
-π ; (6) 10 =
−2
1 10
2.要画一个面积为 要画一个面积为18cm²的矩形，使它的 的矩形， 要画一个面积为 的矩形 长宽之比为3:2，它的长宽应取多少？ 长宽之比为 ，它的长宽应取多少？ 解：设矩形的长宽分别为3x和2x. 设矩形的长宽分别为 和 由题意得， 由题意得，3x·2x=18， ， 所以
(−3)2 = 3 02 =
0
； .
a =a =
2
a (a > 0) 0 (a = 0) . − a ( a < 0)
Hale Waihona Puke 例3化简1 （）
16；
（2）
2
（ - 5） .
2
解： 1 （）
16 = 4 = 4；
2
（2） - 5） = （
5 =5
2
( a) 与
2
a 的的别与联系
2
的别： ） 的别： 1）写法不同 （ （2）读法不同 ）
a -1 0 b 1 2
解：由数轴可知，a<0,b>0,a-b<0, 由数轴可知， 所以原式=-a-b+|a-b| 所以原式 =-a-b+(b-a)=-2a
6.请你比较2 3与3 2的大小.
Q 解： 2 3
( ) = 2 ×（ 3） = 4 × 3 = 12 (3 2 ) = 3 ×（ 2） = 9 × 2 = 18 ∴ (2 3 ) < (3 2 )
在上面的问题中， 在上面的问题中，结果分别是 13 ， S ， 它们都表示一些正数的算术平方根. 2 ， h ，它们都表示一些正数的算术平方根
5
我们知道， 个平方根； 我们知道，一个正数有 两 个平方根； 0的平方根为 0 ；在实数范围内， 在实数范围内， 的平方根为 平方根.因此 开平方时， 因此， 负数 没有 平方根 因此，开平方时， 被开方数只能是 正数 和 0 . 一般地， （ 一般地，我们把形如 a a ≥ 0) 的式 子叫做二次根式 “ 二次根式， 子叫做二次根式，” ”称为二次根号. 称为二次根号
表示a的算术平方 当a>0时， a 表示 的算术平方 时 表示0 根，因此 a > 0 ；当a=0时， a 表示 时 的算术平方根， 这就是说， 的算术平方根，因此 a = 0 .这就是说， 这就是说
（a ≥ 0）是一个 非负数 . a
a≥0是非负数， a ≥ 0 是非负数， 是非负数 也是一个 非负数，所以， 非负数，所以，算术平方根具有双重 非负性. 非负性
1 （ ） x + 2；
（2） 3 + x；
（3） 5x；
答案：（ ） 答案：（1）x≥-2 ：（ （3）x≥0 ）
（4） − x；
（2）x≥-3 ） （4）x≤0 ）
填空： 填空：
( 4)
2
=
2
4
1 3
； ；
1 = 3
( 2) = ( 0) =
2 2
2 0
；
.
性质1： 性质 ：
若羌县中学
史春雷
一般地，如果一个正数 的平方等 一般地，如果一个正数x的平方等 于a，即x²=a，那那这个正数 叫 ， ，那那这个正数x叫 的算术平方根. 做a的算术平方根 a的算术平方根 的算术平方根 的算术平方根 .0的算术平方根是 的算术平方根是0. 记为 a（a > 0） 的算术平方根是 一般地，如果一个数的平方等于 ， 一般地，如果一个数的平方等于a， 那那这个数叫做a的平方根或二次方 那那这个数叫做 的平方根或二次方 这就是说， 那那x 根.这就是说，如果 x 2 = a ， 那那 这就是说 叫做a的平方根 的平方根. （ 叫做 的平方根 记为x = ± a a ≥ 0） .
( a)
2
= a （ a ≥ 0） 表示a的算术平方根的 表示 的算术平方根的
平方，先计算 的算术平方根 再求平方. 的算术平方根， 平方，先计算a的算术平方根，再求平方
表示的是 的平方的算术平方 a = a 表示的是a的平方的算术平方
2
的平方， 根，先计算a的平方，再求算术平方根 先计算 的平方 再求算术平方根.
2 2 2 2 2 2 2 2
∴2 3 < 3 2
是整数， 7. （1） 18 - n 是整数， 求自然数n的值； 求自然数n的值； 是整数， （2） 24n 是整数， 求正整数n的最小值. 求正整数n的最小值.
是完全平方数， 解：（1）由题意知，18-n是完全平方数， ：（ ）由题意知， 是完全平方数 所以18-n=1或4或9或16. 所以 或 或 或 所以n的值为 的值为17或 或 或 所以 的值为 或14或9或2. 是完全平方数， （2）由题意知，24n是完全平方数， ）由题意知， 是完全平方数 24的倍数中最小的完全平方数是 的倍数中最小的完全平方数是144， 的倍数中最小的完全平方数是 ， 所以24n=144，所以 的最小值为 的最小值为6. 所以 ，所以n的最小值为
3 a≥ 2
3 a≥ - . 2
时， 2a + 3在实
数范围内有意义. 数范围内有意义
练习 1.判断下列哪些式子是二次根式 判断下列哪些式子是二次根式. 判断下列哪些式子是二次根式
3 1） a 2 ；（2） m；（3） a；（4） x + 1； 2 （
（5） 5；（6） a - b a ≥ b）；（ 7） - x - 1. （
2
）（4）（ ）（6）是二次根式. 解：（1）（ ）（ ）（ ）是二次根式 ：（ ）（ ）（5）（ 注意：判断一个式子是否是二次根式， 注意：判断一个式子是否是二次根式，不 仅要看形式，还要看是否具备a≥0的条件. a≥0的条件 仅要看形式，还要看是否具备a≥0的条件.
3.当x是怎样的实数时，下列各式在实数 当 是怎样的实数时 是怎样的实数时， 范围内有意义？ 范围内有意义？
学习目标
1.理解二次根式的概念. 2.学习并掌握二次根式的性质.
1.一个三角形两直角边的长分别 一个三角形两直角边的长分别 是2cm和3cm，斜边长应为 13 cm. 和 ， 2.面积为 的正方形的边长为 面积为s的正方形的边长为 面积为
S
.
3.要修建一个面积为 要修建一个面积为6.28m²的圆形喷 要修建一个面积为 的圆形喷 水池， 水池，它的半径为 2 m（π取3.14） （ 取 ） 4.一个物体从高处自由落下，落到地面 一个物体从高处自由落下， 一个物体从高处自由落下 所用的时间t（单位： ） 所用的时间 （单位：s）与开始落下时 的高度h（单位： ）必必关系h=5t².如 的高度 （单位：m）必必关系 如 h . 果用含有h的式子表示 的式子表示t， 果用含有 的式子表示 ，则t= 5
2 1
B(5,3)
o
1
2
3
4
5
6
7
x
AB 2 + AC 2
2 2
= 3 +2 = 13
2009 4.已知 a + 2 + b - 1 = 0，那那（ a + b） 的值为 -1 .
解：由题意知，a+2=0且b-1=0，所以 由题意知， 且 ， 2009 2009 a=-2，b=1， ， ， 所以（ a + b） = - 1） = -1 （ 5.实数 、b在数轴上的位置如图所示， 实数a、 在数轴上的位置如图所示 在数轴上的位置如图所示， 实数 2 化简： 化简： a 2 - b 2 + （ a - b） .
感谢大家的参与！再见！
x= 3
所以它的长宽分别为 3 3和2 3.
y
3.如右图，在平面直角 坐标系中，A（2,3）， B（5,3），C（2,5）是 三角形的三个顶点， 求BC的长. 由题意知， 解：由题意知， AB=5-2=3， AB=5-2=3， AC=5-3=2， ，
所以 BC =
7 6
C(2,5)
5 4 3
A(2,3)
联系： 联系： 1.它们都是二次根式 它们都是二次根式 2.它们都是非负数 它们都是非负数 3.当a≥0时， 当 时
( a)
2
= a = a.
2
练习 1.说出下列各式的值： 说出下列各式的值： 说出下列各式的值
（1 ）
( 3)
2
=
2
3 ； （2） 3 2 = 18 ；
1 1 = 0.3 ； （4） − = 7 7
( a)
2
= a (a ≥ 0) .
例2
计算
1 （）
解：1) (
( 1. 5 ) ；
2
（2） 2 5 .
( 1 .5 )
2
( )
2
2
= 1.5;
2
（2） 2 5
( )
=2 ×
( 5)
2
= 4 × 5 = 20.
填空： 填空：
22 = 2 = 3
性质2： 性质 ：
2
2
2 3
； ；
是怎样的实数时， 例1 当a是怎样的实数时，下列各 是怎样的实数时 式在实数范围内有意义？ 式在实数范围内有意义？