北京市东城区2011届高三第二次模拟考试理科数学2011.5

北京市东城区2011届高三二模理综化学试题可能用到的相对原子质量：H 1 C 12 N 14 O 166．下列说法不正确．．．的是A．淀粉可以制得葡萄糖和酒精B．铝合金的熔点和硬度均高于纯铝C．玻璃、塑料、金属、纸类均是可回收的物品D．硬化油不易被空气氧化而便于储存和运输7．下列做法正确的是A．用无色试剂瓶盛放新制的氯水B．用10 mL量筒量取3.24 mL稀硫酸C．用蒸馏水鉴别溴蒸气和二氧化氮气体D．用氨水清洗做过银镜反应的试管内壁8．下列叙述正确的是Ａ．NH4Cl只含共价键，所以它是共价化合物Ｂ．Al(OH)3是两性氢氧化物，所以它能溶解于盐酸或氨水中Ｃ．硅胶多孔，吸附水份能力强，所以常用作袋装食品的干燥剂Ｄ．元素周期表中氢原子半径最小，所以氢是最活泼的非金属元素9．下列各组物质不能．．按“”所示关系实现转化的是（“”表示反应一步完成）A．B．C．D．10．加热聚丙烯废塑料可以得到碳、氢气、甲烷、乙烯、丙烯、苯和甲苯。

用图所示装置探究废旧塑料的再利用。

下列叙述不正确．．．的是A．聚丙烯的链节是—CH2—CH2—CH2—B．装置乙的试管中可收集到芳香烃C．装置丙中的试剂可吸收烯烃以制取卤代烃D．最后收集的气体可做燃料11．有X、Y、Z三种物质。

常温下分别用Y或Z与X混合时，反应速率几乎相同的是12．下列溶液中各微粒的浓度关系正确的是A．0.1 mol·L-1 Na2S溶液中：2c(Na+)=c(S2－)+c(HS－)+c(H2S)B．0.1 mol·L-1 pH=9的NaNO2溶液中：c(Na+)>c(NO2－)>c(OH－) >c(H+)C．等pH的氨水、NaOH溶液、Ba(OH)2溶液中：c(NH4+)=c(Na+)=c(Ba2+)D．向NH4HCO3溶液中滴加NaOH溶液至pH=7：c(NH4+)+c(Na+)= c(HCO3－)+c(CO32－)25. 苯酚是一种重要的化工原料。

北京市东城区2010—2011学年第二学期高三综合练习（二）理科综合能力测试本试卷分选择题和非选择题两部分，共300分。

考试时长150分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将答题卡交回。

以下数据可供解题时参考：可能用到的相对原子质量：H 1 C 12 N 14 O 16选择题共120分选择题共20小题，每小题6分，共120分。

在每小题列出的四个选项中，选出符合题目要求的一项。

1．下列关于细胞内化合物的叙述不正确．．．的是（）A．由葡萄糖合成的糖原作为储能物质存在于动物细胞中B．由氨基酸缩合形成的蛋白质是细胞和生物体功能的重要体现者C．含有三个高能磷酸键的ATP分子可直接为细胞的生命活动一共能D．多种无机盐离子对维持细胞和生物体的生命活动有重要作用2．下列关于高等动物体内细胞的生命历程的叙述不正确．．．的是（）A．细胞增殖包括物质准备和细胞分裂整个连续的过程B．细胞的分化有利于提高生物体各种生理功能的效率C．细胞在癌变的过程中发生了基因突变和基因重组D，细胞的衰老与凋亡并不能说明动物个体已经衰老3．图—1为人体内基因对性状的控制过程，分析可知（）A．基因l和基因2一般不会出现在人体内的同一个细胞中B．图中①过程需RNA聚合酶的催化，②过程需tRNA的协助C．④⑤过程的结果存在差异的根本原因是血红蛋白结构的不同D．过程①②③表明基因通过控制酶的合成来控制生物体的所有性状4．某种昆虫对经常使用的一种杀虫剂产生了抗药性，下列叙述正确的是（）A．杀虫剂诱发种群中特定个体产生了可遗传的抗药性变异B．在使用杀虫剂之前昆虫种群基因库中就存在抗药性基因C．种群抗药性基因频率在使用此杀虫剂过程中保持不变D．已经具有了抗药性的昆虫种群属于一个新的物种5．血糖平衡对机体生命活动具有重要作用。

图—2为人体部分血糖调控模式图，相关叙述正确的是（）A．通过图中②和⑤过程可同时促进肝糖原的合成和脂肪转化成葡萄糖B．低血糖状态时，除图中途径外还可通过肌糖原的分解使血糖恢复正常C．高血糖状态时，④过程可使胰岛A细胞分泌的胰岛素增多进而使血糖恢复正常D．在血糖调控过程中，胰岛素的作用结果可以通过反馈影响胰岛素的分泌6．下列说法不正确．．．的是（）A．淀粉可以制得葡萄糖和酒精B．铝合金的熔点和硬度均高于纯铝C．玻璃、塑料、金属、纸类均是可回收的物品D．硬化油不易被空气氧化而便于储存和运输7．下列做法正确的是（）A．用无色试剂瓶盛放新制氯水B．用10 mL量筒量取3.24 mL稀硫酸C．用蒸馏水鉴别溴蒸气和二氧化氮气体D．用氨水清洗做过银镜反应的试管内壁8．下叙述正确的是（）A．NH4C1只含共价键，所以它是共价化合物B．Al（OH）3是两性氢氧化物，所以它能溶解于盐酸或氨水中C．硅胶多孔，吸附水份能力强，所以常用作袋装食品的干燥剂D．元素周期表中氢原子半径最小，所以氢是最活泼的非金属元素9．下列各组物质不能．．按“→”所示关系实现转化的是（“→”表示反应一步完成）（）10．加热聚丙烯废塑料可以得到碳、氢气、甲烷、乙烯、丙烯、苯和甲苯。

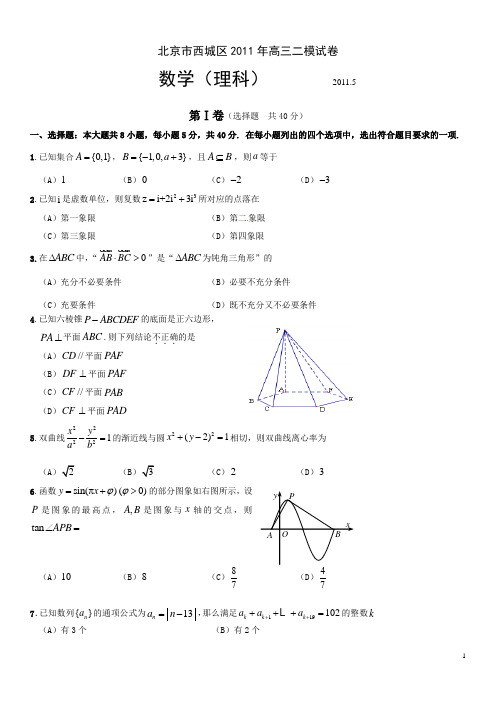
北京市西城区2011年高三二模试卷数学（理科） 2011.5第Ⅰ卷（选择题 共40分）一、选择题：本大题共8小题，每小题5分，共40分. 在每小题列出的四个选项中，选出符合题目要求的一项. 1.已知集合{0,1}A =，{1,0,3}B a =-+，且A B ⊆，则a 等于 （A ）1（B ）0（C ）2- （D ）3-2.已知i 是虚数单位，则复数23z i+2i 3i =+所对应的点落在 （A ）第一象限 （B ）第二象限 （C ）第三象限（D ）第四象限3.在ABC ∆中，“0AB BC ⋅>”是“ABC ∆为钝角三角形”的（A ）充分不必要条件 （B ）必要不充分条件 （C ）充要条件（D ）既不充分又不必要条件4.已知六棱锥P ABCDEF -的底面是正六边形，PA ⊥平面ABC .则下列结论不正确．．．的是 （A ）//CD 平面PAF （B ）DF ⊥平面PAF （C ）//CF 平面PAB （D ）CF ⊥平面PAD5.双曲线22221x y a b-=的渐近线与圆22(2)1x y +-=相切，则双曲线离心率为（A（B（C ）2（D ）3 6.函数sin()(0)y x ϕϕ=π+>的部分图象如右图所示，设P 是图象的最高点，,A B 是图象与x 轴的交点，则tan APB ∠=（A ）10 （B ）8 （C ）87（D ）77．已知数列{}n a 的通项公式为13n a n =-，那么满足119102k k k a a a +++++= 的整数k （A ）有3个（B ）有2个（C ）有1个 （D ）不存在8．设点(1,0)A ，(2,1)B ，如果直线1ax by +=与线段AB 有一个公共点，那么22a b +（A ）最小值为15 （B）最小值为5 （C ）最大值为15（D第Ⅱ卷（非选择题 共110分）二、填空题：本大题共6小题，每小题5分，共30分. 9．在ABC ∆中，若2B A =，:a b =A =_____. 10.在521()x x+的展开式中，2x 的系数是_____. 11．如图，AB 是圆O 的直径，P 在AB 的延长线上，PD切圆O 于点C .已知圆O2OP =，则PC =______；ACD ∠的大小为______.12.在极坐标系中，点(2,)2A π关于直线:cos 1l ρθ=的对称点的一个极坐标为_____.13．定义某种运算⊗，a b ⊗的运算原理如右图所示.设()(0)(2)f x x x x =⊗-⊗. 则(2)f =______；()f x 在区间[2,2]-上的最小值为______.14.数列{}n a 满足11a =，11n n n a a n λ+-=+，其中λ∈R ， 12n = ，，．①当0λ=时，20a =_____；②若存在正整数m ，当n m >时总有0n a <，则λ的取值范围是_____.三、解答题：本大题共6小题，共80分. 解答应写出必要的文字说明、证明过程或演算步骤. 15.（本小题满分13分）已知函数cos 2()sin()4x f x x π=+.（Ⅰ）求函数()f x 的定义域； （Ⅱ）若4()3f x =，求s i n 2x 的值.16.（本小题满分13分）如图，已知菱形ABCD 的边长为6，60BAD ∠=,AC BD O = .将菱形ABCD 沿对角线AC折起，使BD =B ACD -.（Ⅰ）若点M 是棱BC 的中点，求证://OM 平面ABD ； （Ⅱ）求二面角A B D O --的余弦值；（Ⅲ）设点N 是线段BD 上一个动点，试确定N点的位置，使得CN =.17.（本小题满分13分）甲班有2名男乒乓球选手和3名女乒乓球选手，乙班有3名男乒乓球选手和1名女乒乓球选手，学校计划从甲乙两班各选2名选手参加体育交流活动.（Ⅰ）求选出的4名选手均为男选手的概率.（Ⅱ）记X 为选出的4名选手中女选手的人数，求X 的分布列和期望.18.（本小题满分14分）已知函数()(1)e (0)xa f x x x=->，其中e 为自然对数的底数.（Ⅰ）当2a =时，求曲线()y f x =在(1,(1))f 处的切线与坐标轴围成的面积；（Ⅱ）若函数()f x 存在一个极大值点和一个极小值点，且极大值与极小值的积为5e ，求a 的值.19.（本小题满分14分）已知椭圆2222:1x y M a b +=(0)a b >>的离心率为3，且椭圆上一点与椭圆的两个焦点构成的三角形周长为246+．（Ⅰ）求椭圆M 的方程；M（Ⅱ）设直线l 与椭圆M 交于,A B 两点，且以AB 为直径的圆过椭圆的右顶点C ， 求ABC ∆面积的最大值．20.（本小题满分13分）若m A A A ,,,21 为集合2}(,,2,1{≥=n n A 且)n ∈*N 的子集，且满足两个条件： ①12m A A A A = ；②对任意的A y x ⊆},{，至少存在一个},,3,2,1{m i ∈，使}{},{x y x A i = 或}{y . 则称集合组m A A A ,,,21 具有性质P .如图，作n 行m 列数表，定义数表中的第k 行第l 列的数为⎩⎨⎧∉∈=)(0)(1l l kl A k A k a .（Ⅰ）当4n =时，判断下列两个集合组是否具有性质P ，如果是请画出所对应的表格，如果不是请说明理由；集合组1：123{1,3},{2,3},{4}A A A ===； 集合组2：123{2,3,4},{2,3},{1,4}A A A ===. （Ⅱ）当7n =时，若集合组123,,A A A 具有性质P ，请先画出所对应的7行3列的一个数表，再依此表格分别写出集合123,,A A A ；（Ⅲ）当100n =时，集合组12,,,t A A A 是具有性质P 且所含集合个数最小的集合组，求t 的值及12||||||t A A A ++ 的最小值.（其中||i A 表示集合i A 所含元素的个数）北京市西城区2011年高三二模试卷参考答案及评分标准数学（理科） 2011.5一、选择题：本大题共8小题，每小题5分，共40分.二、填空题：本大题共6小题，每小题5分，共30分.9. 30 10. 5 11.1；7512.)4π（或其它等价写法） 13.2-；6- 14.120；(21,2),k k k -∈*N . 注：11、13、14题第一问2分，第二问3分.三、解答题：本大题共6小题，共80分.若考生的解法与本解答不同，正确者可参照评分标准给分. 15.（本小题满分13分） 解：（Ⅰ）由题意，sin()04x π+≠， ………………2分 所以()4x k k π+≠π∈Z ， ………………3分 所以()4x k k π≠π-∈Z ， ………………4分函数()f x 的定义域为{x x ≠,4k k ππ-∈Z }.………………5分（Ⅱ）c o s 2co s 2()sin()sin cos cos sin444x x f x x x x ==πππ++ ………………7分 2sincos xx x=+ ………………8分22sin )sin )sin cos x x x x x x-==-+. ………………10分因为4()3f x =，所以cos sin x x -=. ………………11分 所以，2sin 21(cos sin )x x x =-- ………………12分81199=-= . ………………13分16.（本小题满分13分）（Ⅰ）证明：因为点O 是菱形ABCD 的对角线的交点，所以O 是AC 的中点.又点M 是棱BC 的中点，所以OM 是ABC ∆的中位线，//OM AB . ………………1分 因为OM ⊄平面ABD ,AB ⊂平面ABD ,所以//OM 平面ABD . ………………3分（Ⅱ）解：由题意，3OB OD ==，因为BD =所以90BOD ∠=，OB OD ⊥. ………………4分 又因为菱形ABCD ，所以OB AC ⊥，OD AC ⊥. 建立空间直角坐标系O xyz -，如图所示.(0,3,0),A D (0,0,3)B .所以((AB AD =-=-………………6分设平面ABD 的法向量为n =(,,)x y z ，则有0,0AB AD ⎧⋅=⎪⎨⋅=⎪⎩n n即：30,30z y ⎧-+=⎪⎨-+=⎪⎩令1x =，则y z ==n=(1. ………………7分 因为,AC OB AC OD ⊥⊥,所以AC ⊥平面BOD . 平面BOD 的法向量与AC 平行，所以平面BOD 的法向量为0(1,0,0)=n . ………………8分000cos ,7⋅〈〉===n n n n n n ， 因为二面角A B D O --是锐角，所以二面角A B D O --的余弦值为. ……………9分 （Ⅲ）解：因为N 是线段BD 上一个动点，设111(,,)N x y z ，BN BD λ=，则111(,,3)(0,3,3)x y z λ-=-，所以1110,3,33x y z λλ===-， ……………10分则(0,3,33)N λλ-，,33)CN λλ=-，由CN ==，即29920λλ-+=，…………11分解得13λ=或3λ=， ……………12分 所以N 点的坐标为(0,2,1)或(0,1,2). ……………13分（也可以答是线段BD 的三等分点，2BN ND = 或2BN ND =）17.（本小题满分13分）解：（Ⅰ）事件A 表示“选出的4名选手均为男选手”.由题意知232254()C P A C C = ………………3分11110220=⨯=. ………………5分（Ⅱ）X 的可能取值为0,1,2,3. ………………6分23225431(0)10620C P X C C ====⨯， ………………7分11212333225423337(1)10620C C C C P X C C +⨯⨯+====⨯， ………………9分 21332254333(3)10620C C P X C C ⨯====⨯， ………………10分 (2)1(0)(1)(3)P X P X P X P X ==-=-=-=920=. ………………11分 X………………12分179317()01232020202010E X =⨯+⨯+⨯+⨯=. ………………13分18、（本小题满分14分）解：（Ⅰ）22()e xx ax a f x x-+'=， ………………3分 当2a =时，2222()e xx x f x x -+'=， 12122(1)e e 1f -+'=⨯=，(1)e f =-， 所以曲线()y f x =在(1,(1))f 处的切线方程为e 2e y x =-， ………………5分 切线与x 轴、y 轴的交点坐标分别为(2,0)，(0,2e)-， ………………6分 所以，所求面积为122e 2e 2⨯⨯-=. ………………7分 （Ⅱ）因为函数()f x 存在一个极大值点和一个极小值点，所以，方程20x ax a -+=在(0,)+∞内存在两个不等实根， ………………8分则240,0.a a a ⎧∆=->⎨>⎩ ………………9分 所以4a >. ………………10分 设12,x x 为函数()f x 的极大值点和极小值点，则12x x a +=，12x x a =， ………………11分 因为，512()()e f x f x =，所以，1251212e e e x x x a x a x x --⨯=， ………………12分 即1225121212()e e x x x x a x x a x x +-++=，225e e a a a a a -+=，5e e a =， 解得，5a =，此时()f x 有两个极值点，所以5a =. ………………14分19.（本小题满分14分）解：（Ⅰ）因为椭圆M 上一点和它的两个焦点构成的三角形周长为246+，所以24622+=+c a ， ……………1分又椭圆的离心率为3，即3c a =，所以3c a =， ………………2分所以3a =，c =………………4分所以1b =，椭圆M 的方程为1922=+y x . ………………5分 （Ⅱ）方法一：不妨设BC 的方程(3),(0)y n x n =->，则AC 的方程为)3(1--=x ny . 由22(3),19y n x x y =-⎧⎪⎨+=⎪⎩得0196)91(2222=-+-+n x n x n ， ………………6分 设),(11y x A ，),(22y x B ，因为222819391n x n -=+，所以19327222+-=n n x ， ………………7分 同理可得2219327nn x +-=， ………………8分 所以1961||22++=n n BC ，222961||nn n n AC ++=， ………………10分 964)1()1(2||||212+++==∆n n n n AC BC S ABC ， ………………12分 设21≥+=n n t ，则22236464899t S t t t==≤++， ………………13分当且仅当38=t 时取等号， 所以ABC ∆面积的最大值为83. ………………14分 方法二：不妨设直线AB 的方程x ky m =+.由22,1,9x ky m x y =+⎧⎪⎨+=⎪⎩ 消去x 得222(9)290k y kmy m +++-=， ………………6分 设),(11y x A ，),(22y x B ，则有12229km y y k +=-+，212299m y y k -=+. ① ………………7分因为以AB 为直径的圆过点C ，所以 0CA CB ⋅=.由 1122(3,),(3,)CA x y CB x y =-=-，得 1212(3)(3)0x x y y --+=. ………………8分 将1122,x ky m x ky m =+=+代入上式，得 221212(1)(3)()(3)0k y y k m y y m ++-++-=.将 ① 代入上式，解得 125m =或3m =（舍）. ………………10分 所以125m =（此时直线AB 经过定点12(,0)5D ，与椭圆有两个交点），所以121||||2ABC S DC y y ∆=-12==……………12分 设211,099t t k =<≤+，则ABC S ∆=所以当251(0,]2889t =∈时，ABC S ∆取得最大值83. ……………14分20.（本小题满分13分）（Ⅰ）解：集合组1具有性质P . ………………1分所对应的数表为：………………3分集合组2不具有性质P . ………………4分1 1 0 0 00 1 1 0 0 1因为存在{{2,3}1,2,3,4}⊆，有123{2,3}{2,3},{2,3}{2,3},{2,3}A A A ===∅ ， 与对任意的A y x ⊆},{，都至少存在一个{1,2,3}i ∈，有}{},{x y x A i = 或}{y 矛盾，所以集合组123{2,3,4},{2,3},{1,4}A A A ===不具有性质P . ………………5分（Ⅱ）……………7分123{3,4,5,7},{2,4,6,7},{1,5,6,7}A A A ===. ………………8分 （注：表格中的7行可以交换得到不同的表格，它们所对应的集合组也不同） （Ⅲ）设12,,,t A A A 所对应的数表为数表M ，因为集合组12,,,t A A A 为具有性质P 的集合组， 所以集合组12,,,t A A A 满足条件①和②， 由条件①：12t A A A A = ，可得对任意x A ∈，都存在{1,2,3,,}i t ∈ 有i A x ∈， 所以1=xi a ，即第x 行不全为0，所以由条件①可知数表M 中任意一行不全为0. ………………9分由条件②知，对任意的A y x ⊆},{，都至少存在一个{1,2,3,,}i t ∈ ，使}{},{x y x A i = 或}{y ，所以yi xi a a ,一定是一个1一个0，即第x 行与第y 行的第i 列的两个数一定不同.所以由条件②可得数表M 中任意两行不完全相同. ………………10分因为由0,1所构成的t 元有序数组共有2t个，去掉全是0的t 元有序数组，共有21t-个，又因数表M 中任意两行都不完全相同，所以10021t≤-，所以7t ≥.又7t =时，由0,1所构成的7元有序数组共有128个，去掉全是0的数组，共127个，选择其中的100个数组构造100行7列数表，则数表对应的集合组满足条件①②，即具有性质P .所以7t =. ………………12分 因为12||||||t A A A +++ 等于表格中数字1的个数，所以，要使12||||||t A A A +++ 取得最小值，只需使表中1的个数尽可能少， 而7t =时，在数表M 中，1的个数为1的行最多7行；1的个数为2的行最多2721C =行；1的个数为3的行最多3735C =行； 1的个数为4的行最多4735C =行；1 1 1 1 1 11 1 1 1 1 1 0 0 0 0 0 0 0 0 011 因为上述共有98行，所以还有2行各有5个1，所以此时表格中最少有722133543552304+⨯+⨯+⨯+⨯=个1.所以12||||||t A A A +++ 的最小值为304. ………………14分。

xyO π2π1-1丰台区2011年高三年级第二学期统一练习（二）数学（理科）2011.5一、本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项． 1．在复平面内，复数121iz i-=+对应的点位于 (A) 第一象限 (B)第二象限 (C) 第三象限(D)第四象限2．下列四个命题中，假命题为(A) x ∀∈R ，20x > (B) x ∀∈R ，2310x x ++> (C) x ∃∈R ，lg 0x >(D) x ∃∈R ，122x =3．已知a >0且a ≠1，函数log a y x =，x y a =，y x a =+在同一坐标系中的图象可能是(A)(B) (C) (D)4．参数方程2cos (3sin x y θθθ=⎧⎨=⎩，，为参数)和极坐标方程4sin ρθ=所表示的图形分别是(A) 圆和直线 (B) 直线和直线 (C) 椭圆和直线 (D)椭圆和圆 5．由1,2,3,4,5组成没有重复数字且2与5不相邻的四位数的个数是(A) 120 (B) 84 (C) 60 (D) 486．已知函数sin()y A x ωϕ=+的图象如图所示，则该函数的解析式可能是(A) 441sin()555y x =+(B) 31sin(2)25y x =+(C) 441sin()555y x =-(D) 41sin(2)55y x =+7．已知直线l ：0Ax By C ++=(A ，B 不全为0)，两点111(,)P x y ，222(,)P x y ，若1122()()0Ax By C Ax By C ++++>，且1122Ax By C Ax By C ++>++，则(A) 直线l 与直线P 1P 2不相交(B) 直线l 与线段P 2P 1的延长线相交 (C) 直线l 与线段P 1P 2的延长线相交(D) 直线l 与线段P 1P 2相交OO O O x xxxyyyy1 11 1111 18．已知函数2()2f x x x =-，()2g x ax =+(a >0)，若1[1,2]x ∀∈-，2[1,2]x ∃∈-，使得f (x 1)= g (x 2)，则实数a 的取值范围是 (A) 1(0,]2(B) 1[,3]2(C) (0,3] (D)[3,)+∞二、填空题：本大题共6小题，每小题5分，共30分．9．圆C ：222220x y x y ++--=的圆心到直线3x +4y +14=0的距离是． 10．如图所示，DB ，DC 是⊙O 的两条切线，A 是圆上一点，已知 ∠D =46°，则∠A =．11．函数2cos sin y x x x =-的最小正周期为，最大值 为．12．一个几何体的三视图如图所示，则该几何体的体积是．13．如果执行右面的程序框图，那么输出的a =___．14．如图所示，∠AOB =1rad ，点A l ，A 2，…在OA 上，点B 1，B 2，…在OB 上，其中的每一个实线段和虚线段的长均为1个长度单位，一个动点M 从O 点出发，沿着实线段和以O 为圆心的圆弧匀速运动，速度为l 长度单位／秒，则质点M 到达A 3点处所需要的时间为__秒，质点M 到达A n 点处所需要的时间为__秒．OA 1A 2 A 3 A 4B 1 B 2 B 3 B 4 AB正视图侧视图俯视图A三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15.（本小题共13分）已知等差数列{}n a 的前n 项和为n S ，a 2=4，S 5=35． （Ⅰ）求数列{}n a 的前n 项和n S ；（Ⅱ）若数列{}n b 满足n a n b e =，求数列{}n b 的前n 项和n T ．16.（本小题共14分）张先生家住H 小区，他在C 科技园区工作，从家开车到公司上班有L 1，L 2两条路线（如图），L 1路线上有A 1，A 2，A 3三个路口，各路口遇到红灯的概率均为12；L 2路线上有B 1，B 2两个路口，各路口遇到红灯的概率依次为34，35．（Ⅰ）若走L 1路线，求最多．．遇到1次红灯的概率； （Ⅱ）若走L 2路线，求遇到红灯次数X 的数学期望；（Ⅲ）按照“平均遇到红灯次数最少”的要求，请你帮助张先生从上述两条路线中选择一条最好的上班路线，并说明理由．17.（本小题共13分）已知平行四边形ABCD 中，AB =6，AD =10，BD =8，E 是线段AD 的中点．沿BD 将△BCD 翻折到△BC D '，使得平面BC D '⊥平面ABD ． （Ⅰ）求证：C D '⊥平面ABD ； （Ⅱ）求直线BD 与平面BEC '所成角的正弦值； （Ⅲ）求二面角D BE C '--的余弦值．12A B D E C ' C18.（本小题共13分）已知函数2()ln (2)f x x ax a x =-+-． （Ⅰ）若()f x 在1x =处取得极值，求a 的值； （Ⅱ）求函数()y f x =在2[,]a a 上的最大值．19.（本小题共14分）已知抛物线P ：x 2=2py (p >0)．（Ⅰ）若抛物线上点(,2)M m 到焦点F 的距离为3．（ⅰ）求抛物线P 的方程；（ⅱ）设抛物线P 的准线与y 轴的交点为E ，过E 作抛物线P 的切线，求此切线方程； （Ⅱ）设过焦点F 的动直线l 交抛物线于A ，B 两点，连接AO ，BO 并延长分别交抛物线的准线于C ，D 两点，求证：以CD 为直径的圆过焦点F ．20.（本小题共13分） 用[]a 表示不大于a 的最大整数．令集合{1,2,3,4,5}P =，对任意k P ∈和N*m ∈，定义51(,)[]i f m k ==∑，集合{N*,}A m k P =∈∈，并将集合A 中的元素按照从小到大的顺序排列，记为数列{}n a ． （Ⅰ）求(1,2)f 的值； （Ⅱ）求9a 的值；（Ⅲ）求证：在数列{}n a中，不大于m 00(,)f m k 项．（考生务必将答案答在答题卡上，在试卷上作答无效）海淀区高三年级第二学期期末练习数学（理科） 2011.5选择题 （共40分）一、选择题：本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.复数11i+在复平面上对应的点的坐标是A ．(1,1) B. (1,1)- C. (1,1)-- D. (1,1)-2. 已知全集R,U =集合{}1,2,3,4,5A =,{|2}B x x =∈≥R ，下图中阴影部分所表示的集合为 A {1}B.{0,1} C. {1,2}D. {0,1,2} 3．函数21()log f x x x=-的零点所在区间 A ．1(0,)2 B.1(,1)2C.(1,2)D.(2,3) 4.若直线l 的参数方程为13()24x tt y t =+⎧⎨=-⎩为参数，则直线l 倾斜角的余弦值为A ．45-B ．35-C ．35D ．455. 某赛季甲、乙两名篮球运动员各13场比赛得分情况用茎叶图表示如下：甲 乙 9 8 8 1 7 7 9 9 6 1 0 2 2 5 6 7 9 9 5 3 2 0 3 0 2 3 7 1 0 4根据上图，对这两名运动员的成绩进行比较，下列四个结论中，不正确．．．的是 A ．甲运动员得分的极差大于乙运动员得分的极差B ．甲运动员得分的的中位数大于乙运动员得分的的中位数C ．甲运动员的得分平均值大于乙运动员的得分平均值D ．甲运动员的成绩比乙运动员的成绩稳定6．一个锥体的主视图和左视图如图所示，下面选项中，不．可能是．．．该锥体的俯视图的是7．若椭圆1C ：1212212=+b ya x（011>>b a ）和椭圆2C ：1222222=+b ya x（022>>b a ）的焦点相同且12a a >.给出如下四个结论：① 椭圆1C 和椭圆2C 一定没有公共点； ②1122a b a b >； ③22212221b b a a -=-； ④1212a a b b -<-.其中，所有正确结论的序号是A ．②③④B. ①③④C ．①②④D.①②③8. 在一个正方体1111A B C D A B C D -中，P 为正方形1111A B C D 四边上的动点，O 为底面正方形ABCD 的中心，,M N 分别为,AB BC 中点，点Q 为平面ABCD 内一点，线段1D Q 与OP 互相平分，则满足M Q λ=的实数λ的值有A. 0个B. 1个C. 2个D. 3个非选择题（共110分）二、填空题:本大题共6小题,每小题5分,共30分.9．点(,)P x y 在不等式组2,,2y x y x x ≤⎧⎪≥-⎨⎪≤⎩表示的平面区域内，则z x y =+的最大值为_______.主视图左视图B ACDA1D 1A 1C 1B DCBOPNQ10．运行如图所示的程序框图，若输入4n =，则输出S 的值为 . 11．若4234512345(1)x mx a x a x a x a x a x -=++++， 其中26a =-，则实数m 的值为；12345a a a a a ++++的值为.12．如图，已知O 的弦AB 交半径OC 于点D ，若3AD =，2BD =，且D 为OC 的中点，则CD 的长为 .13．已知数列{}n a 满足1,a t =，120n n a a +-+=(,)t n ∈∈**N N ，记数列{}n a 的前n 项和的最大值为()f t ，则()f t = .14. 已知函数sin ()xf x x=（1）判断下列三个命题的真假： ①()f x 是偶函数；②()1f x <；③当32x π=时，()f x 取得极小值. 其中真命题有____________________；（写出所有真命题的序号） （2）满足()()666n n f f πππ<+的正整数n 的最小值为___________. 三、解答题: 本大题共6小题,共80分.解答应写出文字说明, 演算步骤或证明过程.15.（本小题共13分）已知函数2()coscos f x x x x ωωω=(0)ω>的最小正周期为π.（Ⅰ）求2()3f π的值；（Ⅱ）求函数()f x 的单调区间及其图象的对称轴方程.16.（本小题共13分）某商场一号电梯从1层出发后可以在2、3、4层停靠.已知该电梯在1层载有4位乘客，假设每位乘客在2、3、4层下电梯是等可能的.(Ⅰ)求这4位乘客中至少有一名乘客在第2层下电梯的概率；(Ⅱ)用X 表示4名乘客在第4层下电梯的人数，求X 的分布列和数学期望. 17.(本小题共14分)如图，四棱锥P ABCD -的底面是直角梯形，//AB CD ，AB AD ⊥，PAB ∆和PAD ∆是两个边长为2的正三角形，4DC =，O 为BD 的中点，E 为PA 的中点． (Ⅰ)求证：PO ⊥平面ABCD ；(Ⅱ)求证：//OE 平面PDC ；(Ⅲ)求直线CB 与平面PDC 所成角的正弦值．18. (本小题共14分）已知函数221()()ln 2f x ax x x ax x =--+.()a ∈R . （I ）当0a =时，求曲线()y f x =在(e,(e))f 处的切线方程（e 2.718...=）； （II ）求函数()f x 的单调区间.19．(本小题共13分）在平面直角坐标系xOy 中，设点(,),(,4)P x y M x -，以线段PM 为直径的圆经过原点O .（Ⅰ）求动点P 的轨迹W 的方程；（Ⅱ）过点(0,4)E -的直线l 与轨迹W 交于两点,A B ，点A 关于y 轴的对称点为'A ，试判断直线'A B 是否恒过一定点，并证明你的结论.20. (本小题共13分）对于数列12n A a a a ：，，，，若满足{}0,1(1,2,3,,)i a i n ∈=⋅⋅⋅，则称数列A 为“0-1数列”.定义变换T ，T 将“0-1数列”A 中原有的每个1都变成0，1，原有的每个0都变成1，0. 例如A :1,0,1，则():0,1,1,0,0,1.T A 设0A 是“0-1数列”，令1(),k k A T A -= 12k = ，，3,.(Ⅰ)若数列2A ：1,0,0,1,0,1,1,0,1,0,0,1.求数列10,A A ；(Ⅱ) 若数列0A 共有10项，则数列2A 中连续两项相等的数对至少有多少对？请说明理由；A D OC PBE(Ⅲ)若0A 为0，1，记数列k A 中连续两项都是0的数对个数为k l ，1,2,3,k =⋅⋅⋅.求k l 关于k 的表达式.北京市朝阳区高三年级第二次综合练习数学测试题（理工类）2011.5（考试时间120分钟满分150分）本试卷分为选择题（共40分）和非选择题（共110分）两部分第一部分（选择题共40分）注意事项：1．答第一部分前，考生务必将自己的姓名、考试科目涂写在答题卡上.考试结束时，将试题卷和答题卡一并交回.2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，不能答在试题卷上.一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项. （1）已知全集U =R ，集合{|021}xA x =<<，3{|log 0}B x x =>，则U ()A B I ð=（A ）{|1}x x >（B ）{|0}x x >（C ）{|01}x x <<（D ）{|0}x x <（2）设,x y ∈R ，那么“0>>y x ”是“1>yx”的 （A ）必要不充分条件（B ）充分不必要条件 （C ）充分必要条件 （D ）既不充分又不必要条件（3）三棱柱的侧棱与底面垂直，且底面是边长为2的等边三角形，其正视图(如图所示)的面积为8，则侧视图的面积为（A ） 8 （B ） 4（C）D（4）已知随机变量X 服从正态分布(, 4)N a ，且(1)0.5P X >=，则实数a 的值为（A ）1 （BC ）2（D ）4（5）若一个三位数的十位数字比个位数字和百位数字都大，则称这个数为“伞数”．现从正视图1,2,3,4,5,6这六个数字中任取3个数，组成无重复数字的三位数，其中“伞数”有 （A ）120个（B ）80个（C ）40个（D ）20个（6）点P 是抛物线x y 42=上一动点，则点P 到点(0,1)A -的距离与到直线1-=x 的距离和的最小值是 （ABC ）2 （D ）2（7）已知棱长为1的正方体1111ABCD A BC D -中，点E ，F 分别是棱1BB ，1DD 上的动 点，且1BE D F λ==1(0)2λ<≤．设EF 与AB 所成的角为α，与BC 所成的角为β，则αβ+的最小值（A ）不存在（B ）等于60︒（C ）等于90︒（D ）等于120︒（8）已知点P 是ABC ∆的中位线EF 上任意一点，且//EF BC ，实数x ，y 满足PA xPB yPC ++=0 ．设ABC ∆，PBC ∆，PCA ∆，PAB ∆的面积分别为S ，1S ，2S ，3S ，记11SSλ=，22S S λ=，33S Sλ=．则23λλ⋅取最大值时，2x y +的值为（A ）32（B ）12（C ） 1 （D ）2 第二部分（非选择题共110分）二、填空题：本大题共6小题，每小题5分，共30分.把答案填在题中横线上.（9）已知复数z 满足1iz i =-，则z =. （10）曲线C ：cos 1,sin 1x y θθ=-⎧⎨=+⎩（θ为参数）的普通方程为.（11）曲线233y x =-与x 轴所围成的图形面积为________.(12)已知数列{}n a 满足12a =，且*1120,n n n n a a a a n +++-=∈N ，则2a =；并归纳出数列{}n a 的通项公式n a =.(13)如图，PA 与圆O 相切点A ，PCB 为圆O 的割线，并且不过圆心O ，已知30BPA ∠=，PA =1PC =，则PB =；圆O 的 半径等于．(14)已知函数2()(1)1f x ax b x b =+++-，且(0, 3)a ∈，则对于任意 的b ∈R ，函数()()F x f x x =-总有两个不同的零点的概率是.三、解答题：本大题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程. （15）（本小题满分13分）已知函数2()2sin sin()2sin 12f x x x x π=⋅+-+()x ∈R . （Ⅰ）求函数()f x 的最小正周期及函数()f x 的单调递增区间；（Ⅱ）若0()23x f =，ππ(, )44x ∈-，求0cos 2x 的值.（16）（本小题满分13分）为了防止受到核污染的产品影响我国民众的身体健康，要求产品在进入市场前必须进行两轮核辐射检测，只有两轮都合格才能进行销售，否则不能销售.已知某产品第一轮检测不合格的概率为16，第二轮检测不合格的概率为110，两轮检测是否合格相互没有影响. （Ⅰ）求该产品不能销售的概率；（Ⅱ）如果产品可以销售，则每件产品可获利40元；如果产品不能销售，则每件产品亏损80元（即获利-80元）.已知一箱中有产品4件，记一箱产品获利X 元，求X 的分布列，并求出均值E (X ).（17）（本小题满分13分）在长方形11AA B B 中，124AB AA ==，C ，1C 分别是AB ，11A B 的中点（如图1）. 将此长方形沿1CC 对折，使二面角11A CC B --为直二面角，D ，E 分别是11A B ，1CC 的中点（如图2）.（Ⅰ）求证：1C D ∥平面1A BE ； （Ⅱ）求证：平面1A BE ⊥平面11AA B B ； （Ⅲ）求直线1BC 与平面1A BE 所成角的正弦值.(18)（本小题满分13分）设函数2()ln ()f x x x a =+-，a ∈R . （Ⅰ）若0a =，求函数()f x 在[1,]e 上的最小值；（Ⅱ）若函数()f x 在1[, 2]2上存在单调递增区间，试求实数a 的取值范围； （Ⅲ）求函数)(x f 的极值点.(19)（本小题满分14分）已知椭圆2222:1(0)x y C a b a b +=>>经过点(2, 1)A ，离心率为2．过点(3, 0)B 的直线l 与椭圆C交于不同的两点,M N ． （Ⅰ）求椭圆C 的方程； （Ⅱ）求BM BN ⋅的取值范围；（Ⅲ）设直线AM 和直线AN 的斜率分别为AM k 和AN k ，求证:AM AN k k +为定值．(20)（本小题满分14分）对于正整数, a b ，存在唯一一对整数q 和r ，使得a bq r =+，0r b <≤.特别地，当0r =时，称b 能整除a ，记作|b a ，已知{1, 2, 3,,23}A =⋅⋅⋅.（Ⅰ）存在q A ∈，使得201191 (091)q r r =+<≤，试求,q r 的值；图（1）（Ⅱ）求证：不存在这样的函数:{1,2,3}f A →，使得对任意的整数12,x x A ∈，若12||{1,2,3}x x -∈，则12()()f x f x ≠；（Ⅲ）若B A ⊆，12)(=B card （()card B 指集合B 中的元素的个数），且存在,a b B ∈，b a <，|b a ，则称B 为“和谐集”.求最大的m A ∈，使含m 的集合A 的有12个元素的任意子集为“和谐集”，并说明理由.北京市西城区2011年高三二模试卷数学（理科）2011.5第Ⅰ卷（选择题 共40分）一、选择题：本大题共8小题，每小题5分，共40分. 在每小题列出的四个选项中，选出符合题目要求的一项. 1.已知集合{0,1}A =，{1,0,3}B a =-+，且A B ⊆，则a 等于 （A ）1（B ）0（C ）2-（D ）3-2.已知i 是虚数单位，则复数23z i+2i 3i =+所对应的点落在（A ）第一象限 （B ）第二象限 （C ）第三象限（D ）第四象限3.在ABC ∆中，“0AB BC ⋅>”是“ABC ∆为钝角三角形”的（A ）充分不必要条件 （B ）必要不充分条件 （C ）充要条件（D ）既不充分又不必要条件4.已知六棱锥P ABCDEF -的底面是正六边形，PA ⊥平面ABC .则下列结论不正确．．．的是 （A ）//CD 平面PAF （B ）DF ⊥平面PAF （C ）//CF 平面PAB （D ）CF ⊥平面PAD5.双曲线22221x y a b-=的渐近线与圆22(2)1x y +-=相切，则双曲线离心率为（A（B（C ）2（D ）3 6.函数sin()(0)y x ϕϕ=π+>的部分图象如右图所示，设P 是图象的最高点，,A B 是图象与x 轴的交点，则tan APB ∠=（A ）10 （B ）8 （C ）87（D ）77．已知数列{}n a 的通项公式为13n a n =-，那么满足119102k k k a a a +++++= 的整数k（A ）有3个 （B ）有2个 （C ）有1个（D ）不存在8．设点(1,0)A ，(2,1)B ，如果直线1ax by +=与线段AB 有一个公共点，那么22a b +（A ）最小值为15 （B ）最小值为5 （C ）最大值为15（D第Ⅱ卷（非选择题 共110分）二、填空题：本大题共6小题，每小题5分，共30分. 9．在中，若2B A =，:a b =A =_____. 10.在521()x x+的展开式中，2x 的系数是_____. 11．如图，AB 是圆O 的直径，P 在AB 的延长线上，PD切圆O 于点C .已知圆O 2OP =，则PC =______；ACD ∠的大小为______.12.在极坐标系中，点(2,)2A π关于直线:cos 1l ρθ=的对称点的一个极坐标为_____.13．定义某种运算⊗，a b ⊗的运算原理如右图所示.ABC ∆设()(0)(2)f x x x x =⊗-⊗. 则(2)f =______；()f x 在区间[2,2]-上的最小值为______.14.数列{}n a 满足11a =，11n n n a a n λ+-=+，其中λ∈R ， 12n = ，，．①当0λ=时，20a =_____；② 若存在正整数m ，当n m >时总有0n a <，则λ的取值范围是_____.三、解答题：本大题共6小题，共80分. 解答应写出必要的文字说明、证明过程或演算步骤. 15.（本小题满分13分）已知函数cos 2()sin()4x f x x π=+.（Ⅰ）求函数()f x 的定义域； （Ⅱ）若4()3f x =，求s i n 2x 的值.16.（本小题满分13分）如图，已知菱形ABCD 的边长为6，60BAD ∠=,AC BD O = .将菱形ABCD 沿对角线AC 折起，使BD =B ACD -.（Ⅰ）若点M 是棱BC 的中点，求证://OM 平面ABD ； （Ⅱ）求二面角A B D O --的余弦值；（Ⅲ）设点N 是线段BD 上一个动点，试确定N点的位置，使得CN =.17.（本小题满分13分）甲班有2名男乒乓球选手和3名女乒乓球选手，乙班有3名男乒乓球选手和1名女乒乓球选手，学校计划从甲乙两班各选2名选手参加体育交流活动.M（Ⅰ）求选出的4名选手均为男选手的概率.（Ⅱ）记X 为选出的4名选手中女选手的人数，求X 的分布列和期望.18.（本小题满分14分）已知函数()(1)e (0)xa f x x x=->，其中e 为自然对数的底数.（Ⅰ）当2a =时，求曲线()y f x =在(1,(1))f 处的切线与坐标轴围成的面积；（Ⅱ）若函数()f x 存在一个极大值点和一个极小值点，且极大值与极小值的积为5e ，求a 的值.19.（本小题满分14分）已知椭圆2222:1x y M a b +=(0)a b >>且椭圆上一点与椭圆的两个焦点构成的三角形周长为246+．（Ⅰ）求椭圆M 的方程；（Ⅱ）设直线l 与椭圆M 交于,A B 两点，且以AB 为直径的圆过椭圆的右顶点C ， 求ABC ∆面积的最大值．20.（本小题满分13分）若m A A A ,,,21 为集合2}(,,2,1{≥=n n A 且)n ∈*N 的子集，且满足两个条件： ①12m A A A A = ；②对任意的A y x ⊆},{，至少存在一个},,3,2,1{m i ∈，使}{},{x y x A i = 或}{y . 则称集合组m A A A ,,,21 具有性质P .如图，作n 行m 列数表，定义数表中的第k 行第l 列的数为⎩⎨⎧∉∈=)(0)(1l l kl A k A k a .（Ⅰ）当4n =时，判断下列两个集合组是否具有性质P ，如果是请画出所对应的表格，如果不是请说明理由；集合组1：123{1,3},{2,3},{4}A A A ===； 集合组2：123{2,3,4},{2,3},{1,4}A A A ===. （Ⅱ）当7n =时，若集合组123,,A A A 具有性质P ，请先画出所对应的7行3列的一个数表，再依此表格分别写出集合123,,A A A ；（Ⅲ）当100n =时，集合组12,,,t A A A 是具有性质P 且所含集合个数最小的集合组，求t 的值及12||||||t A A A ++ 的最小值.（其中||i A 表示集合i A 所含元素的个数）北京市东城区2010-2011学年第二学期高三综合练习（二）数学 （理科）第Ⅰ卷（选择题 共40分）一、本大题共8小题，每小题5分，共40分。

北京市东城区2010-2011学年第二学期高三综合练习(一)数 学(理科)本试卷分为第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷1至2页，第Ⅱ卷3至5页，共150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷（选择题 共40分）一、本大题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

1．“x ＞2”是“x 2＞4”的 （A ）充分不必要条件 （B ）必要不充分条件 （C ）充要条件 （D ）既不充分也不必要条件2．已知数列{a n }为等差数列，且a 1=2，a 2+a 3=13，则a 4+a 5+a 6等于 （A ）40 （B ）42 （C ）43 （D ）45 3．已知函数f (x )对任意的x ∈R 有f (x )+f (―x )=0，且当x ＞0时，f (x )=ln(x +1)，则函数f (x )的图象大致为4．已知平面上不重合的四点P ，A ，B ，C 满足PA PB PC ++=0，且AB AC m A P +=，那么实数m 的值为（A ）2 （B ）3（C ）4（D ）55．若右边的程序框图输出的S 是126，则条件①可为 （A ）n ≤5 （B ）n ≤6（C ）n ≤7 （D ）n ≤86．已知(,)2παπ∈，1tan()47πα+=，那么sin α+cos α的值为 （A ）15-（B ）75 （C ）75-（D ）347．已知函数131()()2xf x x =-，那么在下列区间中含有函数f (x )零点的是 （A ）1(0,)3（B ）11(,)32（C ）12(,)23（D ）2(,1)38．空间点到平面的距离定义如下：过空间一点作平面的垂线，这点和垂足之间的距离叫做这个点到这个平面的距离。

已知平面α，β，γ两两互相垂直，点A ∈α，点A 到平面β，γ的距离都是3，点P 是α上的动点，且满足P 到β的距离是P 到点A 距离的2倍，则点P 到平面γ的距离的最大值是（A ）3（B（C ）3（D ）6第Ⅱ卷（共110分）二、填空题：本大题共6小题，每小题5分，共30分。

北京东城区示范校2011届高三第二学期第二次联考数学（理）2011年3月学校_____________班级_______________姓名______________考号___________ 本试卷分第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷1至2页，第Ⅱ卷3至5页，共150分．考试时长120分钟．考生务必将答案答在答题卡上，在试卷上作答无效．考试结束后，将本试卷和答题卡一并交回．第Ⅰ卷（选择题 共40分）一、本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．（1）若集合{} 1A x x =>，{} 0B x x =≥，全集U =R ，则()RA B 等于（ ）（A ）{}11x x -≤≤ （B ）{}0x x ≥ （C ）{}01x x ≤≤ （D ）∅（2）“1m =”是“直线0x y -=和直线0x my +=互相垂直”的 （ ）（A ）充分不必要条件 （B ）必要不充分条件（C ）充要条件 （D ）既不充分也不必要条件（3）已知各项不为0的等差数列{}n a 满足22712220a a a -+=，数列{}n b 是等比数列，且77b a =，则311b b 等于 （ ）（A ）16 （B ）8 （C ）4 （D ）2（4）某程序框图如图所示，现输入如下四个函数：2()f x x =，1()f x x=，()e xf x =，()sin f x x =，则可以输出的函数是 （ ） （A ）2()f x x = （B ）1()f x x=（C ）()e xf x = （D ）()sin f x x =（5）如果三位正整数如“abc ”满足,a b b c <>，则这样的三位数称为凸数（如120,352） 那么，所有的三位凸数的个数为 （ ）（A ）240 （B ）204 （C ）729 （D ）920（6）一个几何体的三视图如图所示，则这个几何体的体积为 （ ）(A) 1 (B) 23(C) 56 (D) 13（7）已知向量()2,1x x +a =，()1,x t -b =，若函数()f x =⋅a b 在区间()1,1-上是增函数，则实数t 的取值范围是 （ ） （A ）[)5,+∞ （B ）()5,+∞ （C ）(],5-∞ （C ）(),5-∞（8） 定义函数()y f x =，x D ∈．若存在常数c ，对任意1x D ∈，存在唯一的2x D ∈，使得()()122f x f x c +=，则称函数()f x 在D 上的算术平均数为c ．已知()ln f x x =，[]2,8x ∈，则()ln f x x =在[]2,8上的算术平均数为 （ ）（A ）ln 2 （B ）ln 4 （C ）ln 5 （D ）ln 8第Ⅱ卷（共110分）二、填空题：本大题共6小题，每小题5分，共30分． （9）复数2i1iz -=+= ；其所确定的点Z 位于复平面的第______象限． （10）右图是样本容量为200的频率分布直方图． 根据样本的频率分布直方图估计，样本数据落在[)6,14内的频数为 ；数据落在[)2,14内的概率约为 ．（11）若抛物线()20y ax a =>的焦点与双曲线22172x y -=的一个焦点相同，则该抛物线的方程为______________． （12）已知在极坐标系下，点π2π1,,3,,33A B O ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭是极点，则,A B 两点间的距离 AB = _____________； AOB ∆的面积等于_______．（13）如图，已知AB 是圆O 的直径，4AB =，C 为圆上任意一点，过C 点做圆的切线分别与过,A B 两点的切线交于,P Q 点，则CP CQ ⋅=________________．（14）如图，在正方体1111ABCD A BC D -中，E ，F ，G ，H ，M 分别是棱AD ，1DD ，111,D A A A AB ，的中点，点N 在四边形EFGH 的四边及其内部运动，则当N 只需满足条件________时，就有11MN AC ⊥；当N 只需满足条件________时，就有MN ∥平面11B D C ．三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． （15）（本小题共13分）已知函数()22cos cos f x x x x a =++，且π46f ⎛⎫= ⎪⎝⎭． （Ⅰ）求a 的值； （Ⅱ）当ππ43x -≤≤时，求函数()f x 的值域．（16）（本小题共13分）某单位在2011新年联欢会上举行一个抽奖活动：甲箱中装有3个红球，2个黑球，乙箱中装有2个红球4个黑球，参加活动者从这两个箱子中分别摸出1个球，如果摸到的都是红球则获奖．（Ⅰ）求每个活动参加者获奖的概率；（Ⅱ）某办公室共有5人，每人抽奖1次，求这5人中至少有3人获奖的概率．（17）（本小题共14分）如图，在四棱柱1111ABCD A BC D -中，底面ABCD 是正方形，侧棱与底面垂直，点O是正方形ABCD 对角线的交点，124AA AB ==，点E ，F 分别在1CC 和1A A 上，且1CE A F =．（Ⅰ）求证：1B F ∥平面BDE ； （Ⅱ）若1AO BE ⊥，求CE 的长； （Ⅲ）在（Ⅱ）的条件下，求二面角1A BE O --的余弦值．（18）（本小题共13分）已知函数()ln (mf x x m x=-∈R ）． （Ⅰ）求函数()f x 的定义域，并讨论函数()f x 的单调性；（Ⅱ）问是否存在实数m ，使得函数()f x 在区间[]1,e 上取得最小值3？请说明理由．（19）（本小题共14分）已知椭圆的的右顶点为A ，离心率12e =，过左焦点()1,0F -作直线l 与椭圆交于点P ，Q ，直线AP ，AQ 分别与直线 4x =-交于点,M N ． (Ⅰ)求椭圆的方程；(Ⅱ)证明以线段MN 为直径的圆经过焦点F ．(20)(本小题共13分)对数列{}n a ，规定{}n a ∆为数列{}n a 的一阶差分数列，其中1(n n n a a a n +∆=-∈N *)．对正整数k ，规定 {}kn a ∆为{}n a 的k 阶差分数列，其中()1111k k k k n n n n a a a a ---+∆=∆-∆=∆∆．（Ⅰ）若数列{}n a 的首项11a =，且满足212n n n n a a a +∆-∆+=-，求数列{}n a 的通项公式； （Ⅱ）对（Ⅰ）中的数列{}n a ，若数列{}n b 是等差数列，使得12311231n nn n n n nn n n bC b C b C b C b C a --+++⋅⋅⋅++= 对一切正整数n ∈N *都成立，求n b ；（Ⅲ） 在（Ⅱ）的条件下，令()21,n n c n b =-设312123,n n nc c c c T a a a a =+++⋅⋅⋅+若n T m <成立，求最小正整数m 的值．2010-2011学年度东城区示范校综合练习答案高三数学 （理科）一、选择题1.C2.C3.A4.D5.A6.C7.A8.B二、填空题 9．13i 22-，4 10．136；0.76 11． 212y x = 1213．4CP CQ ⋅= 14．点N 在EG 上；点N 在EH 上 （填空题，第一空3分，第二空2分）三、解答题 15．解：（Ⅰ）由π46f ⎛⎫=⎪⎝⎭，可得21242a ⨯+=⎝⎭,—————————2分 ∴ 1a =． ——————————4分（Ⅱ）()22cos cos 1f x x x x =++cos23sin 22x x =++ π2sin 226x ⎛⎫=++ ⎪⎝⎭．——————————————8分 ∵ ππ43x -≤≤，∴ππ5π2336x -≤+≤， ∴ 3πsin 2126x ⎛⎫-≤+≤ ⎪⎝⎭，—————————————11分 ∴ ()234f x -≤≤，所以，函数()f x 的值域为23,4⎡⎤-⎣⎦．—————————13分16． 解：（Ⅰ）设事件1A 表示从甲箱中摸出红球，事件2A 表示从乙箱中摸出红球．因为从甲箱中摸球的结果不影响从乙箱中摸球的结果，所以1A 和2A 相互独立．()()12321,,563p A p A ===所以 121231()()()0.253P P AA P A P A ===⨯=（获奖）．————7分 （Ⅱ）设X 为5人中获奖的人次，则(5,0.2)XB ， —————————9分(3)(3)(4)(5)P X P X P X P X ≥==+=+=33244555550.2(10.2)0.2(10.2)0.2C C C =⋅⋅-+⋅⋅-+⋅1813125=． 所以，5人中至少有3人获奖的概率为1813125． ————————13分 17．解：（Ⅰ）证明：取1BE CE =，连结1EE 和1AE ,∴1EE BC =，1EE ∥BC ，BC AD =，BC ∥AD ， ∴1EE AD =，1EE ∥AD ． ∴四边形1AE ED 为平行四边形， ∴1AE ∥DE ，在矩形11A ABB 中，11A F BE =， ∴四边形11B FAE 为平行四边形． ∴1B F ∥1AE ，1B F ∥DE ．∵DE ⊂平面BDE ，1B F ⊄平面BDE ，∴1B F ∥平面BDE ． ————————4分 （Ⅱ）连结OE ，在正四棱柱1111ABCD A BC D -中， 1AA ⊥平面ABCD ， ∴1AA BD ⊥，BD AC ⊥， ∴BD ⊥平面1A AO ， ∴1BD AO ⊥．由已知1AO BE ⊥，得1AO ⊥平面BDE ． ∴190AOE ∠=，190AOA EOC ∠+∠=， 在△1A AO 与△OCE 中， 1EOC OA A ∠=∠，1ECO OAA ∠=∠， ∴△1A AO ∽△OCE ∴1A A AO OC CE =，12CE =．—————————9分 （Ⅲ）以A 为原点，AB ，AD ，1AA 所在直线为x ，y ，z轴，建立空间直角坐标系．11(2,0,0),(2,2,),(0,0,4),(1,1,0)2B E A O ．1117(1,1,4),(2,0,4),(2,2,)2OA A B A E =--=-=-，由（Ⅱ）知1OA 为平面OBE 的一个法向量， 设(,,)x y z =n 为平面1A BE 的一个法向量，则 1100A B A E ⎧⋅=⎪⎨⋅=⎪⎩n n ，即 24072202x z x y z -=⎧⎪⎨+-=⎪⎩， 令1z =，所以 1(2,,1)4=-n ．∴12cos ,6OA <>=n ，∵二面角1A BE O --的平面角为锐角，∴二面角1A BE O --的余弦值为26． —————————13分18． 解：（Ⅰ）函数()f x 的定义域为()0,+∞，且 ()'221m x m f x x x x+=+=． 令()'0fx =，得x m =-． ——————————————2分当0m ≥时，0x m +>，()'20x mf x x+=>，函数()f x 在()0,+∞上是增函数；当0m <时，在区间()0,m -上()'0f x <，函数()f x 在()0,m -上是减函数；在区间(),m -+∞上()'0fx >，函数()f x 在(),m -+∞上是增函数．———6分（Ⅱ）由（Ⅰ）知()'2x mfx x +=， （1）若1m ≥-，则在区间[]1,e 上()'0f x ≥，函数()f x 在[]1,e 上是增函数，此时，()f x 取最小值()1f ，由()13f m =-=，得[)31,m =-∉-+∞；————————8分 （2）若e,m ≤-则在区间[]1,e 上()'0f x ≤，函数()f x 在[]1,e 上是减函数，此时，()f x 取最小值()e f ，由()e 13emf =-=，得(]2e ,e m =-∈-∞-；———————10分 （3）若e 1m -<<-，则在区间[)1,m -上()'0f x ≤，函数()f x 在[)1,m -上是减函数，在区间(),m -+∞上()'0fx ≥，函数()f x 在(),m -+∞上是增函数，此时，()f x 取最小值()f m -，由()()ln 13f m m -=-+=，得2e m =∉()e,1--；——————12分综上所述，存在实数2e m =-，使得()f x 在区间[]1,e 上取得最小值3．——————————13分19． (Ⅰ)解： 由已知 11,,2c c a == ∴2,a b ==，∴ 椭圆方程为22143x y +=．——————————————5分 (Ⅱ) 设直线l 方程为 ()1y k x =+，由 ()221,1,43y k x x y ⎧=+⎪⎨+=⎪⎩ 得()22223484120k x k x k +++-=．设()()1122,,,P x y Q x y ，则221212228412,3434k k x x x x k k-+=-=++．—————7分 设()()4,,4,M N M y N y --，则由,,A P M 共线，得1111,42M y y y x x -=--- 有 1162M y y x =--．同理 2262N y y x =--． ∴ ()()()()2121212121212361362224M N k x x x x y y y y x x x x x x +++⎡⎤⎣⎦==---++．——————9分()()()()212121212222222222223,3,9361 92441283613434936 990.412836243434M N M N FM FN y y y y k x x x x x x x x k k k k k k k k k k k ⋅=-⋅-=++++⎡⎤⎣⎦=+-++⎡⎤--+⎢⎥++⨯⎣⎦=+=-=-++++∴FM FN ⊥，即FM FN ⊥，以线段MN 为直径的圆经过点F ；————12分当直线l 的斜率不存在时，不妨设()()4,3,4,3M N ---．则有()()3,33,3990FM FN ⋅=-⋅--=-=,∴ FM FN ⊥，即FM FN ⊥，以线段MN 为直径的圆经过点F ．综上所述，以线段MN 为直径的圆经过定点F ． ———————————14分 20． 解：（Ⅰ）由212n n n n a a a +∆-∆+=-及21n n n a a a +∆=∆-∆，得 2n n n a a ∆-=， ∴122,n n n a a +-= ∴111,222n n n n a a ++-= ———————————————2分 ∴数列2n na ⎧⎫⎨⎬⎩⎭是首项为1,2公差为12的等差数列， ∴()111,222n n a n =+-⨯ 12n n a n -=⋅．————————4分 （Ⅱ）∵ 12311231n nn n n n n n n n bC b C b C b C b C a --+++⋅⋅⋅++=，∴ 1231112312n nn n n n n nn n bC b C b C b C b C n ---+++⋅⋅⋅++=⋅．∵11 k k n n kC nC --=，()()123101211111121111112312.n n n n n n n n n n n n n n n n n n C C C n C nC nC nC nC nC n CCCCn ------------∴+++⋅⋅⋅+-+=+++⋅⋅⋅+=+++⋅⋅⋅+=⋅∴ n b n =．————————————9分（Ⅲ）由（Ⅱ）得 21135211222n n n T --=+++⋅⋅⋅+， ① 有 2311352122222n nn T -=+++⋅⋅⋅+， ②①-② 得 2322111112112111322222222n n n n n n n T ----=+++++⋅⋅⋅+-=--， ∴311216622n n n n T ---=--<， ——————————10分又21135211222n n n T --=+++⋅⋅⋅+，∴10n n T T +->，∴{}n T 是递增数列，且6351116522T =-->， ∴ 满足条件的最小正整数m 的值为6．————————13分。

2011北京高考数学理科试卷分析题号章节内容分值高中所有章节考分汇总1 集合 52 复数 5 章节分值3 极坐标 57大章函数204 算法框图5 三角函数185 平面几何 5 数列186 函数（分段函数） 5 立体几何147 三视图 5 解析几何148 创新题（函数、画图法） 5 导数139 解三角形 5 统计概率1310 平面向量 511 数学通项、求和公式 510小章集合 512 排列组合 5 复数 513 函数-数形结合 5 极坐标 514 创新题（解析几何、对称性） 5 算法与框图 515 三角函数（周期、最值）13 平面几何 516 立体几何（垂直、线线角）14 平面向量 517 统计（茎叶图、方差、概率、期望）13 三视图 518 导数（单调性、最值）13 排列组合 519 解析（椭圆、韦达定理、最值）14 线性规划020 创新题（数列、充分、必要条件）13 不等式0 说明：2011北京理科卷考点全面，，虽然"线性规划"、"不等式"两个小章未考到，但其中包含的图形处理技巧和最值思想，在第13题函数题需要用到数形结合和19题解析几何大题最后的最值问题中有所体现，所以今年的高考题考到了几乎所有章节。

对于学生而言，每个章节都不能遗漏。

考试难度和计算量总体上比平时的期中期末考试、一、二模更简单：1.小题：前14道小题中，只有第8题和第14题需要多思考才能做对，方法很常规，并没有设置障碍。

其他12个小题全是常规题型，非常容易得分，只要保证计算不错，中等基础的学生能拿到12个题满分。

2.大题：在后面的6个大题80分的考点中，前三个大题考的基础题型，大部分考生不算错的情况下能够得满分；从后三个大题才开始设置难度，拉开了学生层次。

第一题：三角函数大题依然考的热点考点，化简和求最值，学生基础中等偏下水平即可做对。

第二题：立体几何也是常见考点，垂直和角的问题，今年没有考二面角，考的线线角更简单，基础弱的学生甚至可以用几何向量法做出这三问，顺利拿到14分。

东城区2010-2011学年度综合练习（一）高三数学 （理科）学校_____________班级_______________姓名______________考号___________ 本试卷分第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷1至2页，第Ⅱ卷3至5页，共150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷（选择题 共40分）一、本大题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

（1）“2x >”是“24x >”的（A ）充分非必要条件 （B ）必要非充分条件 （C ）充要条件（D ）既不充分也不必要条件（2）已知数列{}n a 为等差数列，且12a =，2313a a +=，那么则456a a a ++等于（A ）40 （B ）42 （C ）43 （D ）45（3）已知函数()f x 对任意的x ∈R 有()()0f x f x +-=，且当0x >时，()ln(1)f x x =+，则函数()f x 的大致图像为（A ）（B ）（C ） （D ）（4）已知平面上不重合的四点P ，A ，B ，C 满足0PA PB PC ++= ，且AB AC m AP +=，那么实数m 的值为（A ）2 （B ）3 （C ）4 （D ）5（5）若右边的程序框图输出的S 是126，则条件①可为A ．5n ≤B ．6n ≤C ．7n ≤D ．8n ≤（6）已知(,)2απ∈π,1tan()47απ+=,那么ααcos sin +的值为（A ）51-（B ）57（C ）57- （D ）43（7）已知函数31)21()(x x f x-=，那么在下列区间中含有函数)(x f 零点的是（A ）)31,0( （B ）)21,31(（C ）)32,21( （D ）)1,32(（8）空间点到平面的距离定义如下：过空间一点作平面的垂线，这个点和垂足之间的距离叫做这个点到这个平面的距离．已知平面α，β，γ两两互相垂直，点A ∈α，点A 到β，γ的距离都是3，点P 是α上的动点，满足P 到β的距离是到P 到点A 距离的2倍，则点P 的轨迹上的点到γ的距离的最小值是 （A ） 33- （B ）323- （C ）36-（D ）340 50 60 70 80 90 体重(kg)频率A第Ⅱ卷（共110分）二、填空题：本大题共6小题，每小题5分，共30分。

数学（理科） 参考答案及评分标准 2011.4一、选择题（本大题共8小题，每小题5分，共40分）（1）B （2）B （3）A （4）C（5）C （6）B （7）B （8）C二、填空题（本大题共6小题，每小题5分，共30分）（9） 1- （10）3（11）5.64 32 （12）15 （13）3 （14）65 n -70注：两个空的填空题第一个空填对得2分，第二个空填对得3分．北京市东城区2011年高三一模试卷数学（理科） 参考答案及评分标准 2011.4一 选择题：本大题共8小题，每小题5分，共40分.二 填空题：本大题共6小题，每小题5分，共30分数学（理科） 参考答案及评分标准 2012.4一、选择题（本大题共8小题，每小题5分，共40分）（1）D （2）A （3）A （4）B（5）C （6）C （7）D （8）A二、填空题（本大题共6小题，每小题5分，共30分）（9）(0,),tan sin 2x x x π∀∈≤ （10（11）84 乙（12） 60o （13） 14x =- 2 （14新课标第一网注：两个空的填空题第一个空填对得2分，第二个空填对得3分．北京市东城区2012年高三二模试卷数 学（理科） 参考答案及评分标准 2012. 5一、选择题（本大题共8小题，每小题5分，共40分）（1）A （2）B （3）D （4）A（5）C （6）B （7）D （8）C二、填空题（本大题共6小题，每小题5分，共30分）（9）1- （10）(1,0) 2 （11）)3,1(- （12）125（13）2 （14）③④ 注：两个空的填空题第一个空填对得3分，第二个空填对得2分．数 学（理科） 参考答案及评分标准 2013. 4一、选择题（本大题共8小题，每小题5分，共40分）（1）C （2）B （3）C （4）A（5）C （6）D （7）D （8）C二、填空题（本大题共6小题，每小题5分，共30分）（9）45- （10）1 （11）(3,0)（12）75+ （13）乙 （14）2 22n -注：两个空的填空题第一个空填对得3分，第二个空填对得2分．北京市东城区2013年高三二模试卷数 学（理科） 参考答案及评分标准 2013. 5一、选择题（本大题共8小题，每小题5分，共40分）（1）B （2）C （3）A （4）D （5）D （6）B （7）D （8）C \二、填空题（本大题共6小题，每小题5分，共30分）（9）32- （10）1 （11）12 152（12）2 （13）150 （14）①③注：两个空的填空题第一个空填对得3分，第二个空填对得2分．数 学（理科）参考答案及评分标准 2014. 4一、选择题（本大题共8小题，每小题5分，共40分） 1．C 2．C 3．D 4．D5．A 6．B 7．C 8．B二、填空题（本大题共6小题，每小题5分，共30分） 9．116 10．30︒11．78 12．2()6=-+f x x ；(20)(2)-+∞U ，，13．24 14北京市东城区2014年高三二模试卷数 学（理科）参考答案及评分标准 2014. 5一、选择题（本大题共8小题，每小题5分，共40分）（1）B （2）A （3）C （4）D（5）D （6）C （7）C （8）D二、填空题（本大题共6小题，每小题5分，共30分）（9）35- （10）4 60o（11）14 （12）（13）3（14）6 注：两个空的填空题第一个空填对得3分，第二个空填对得2分．。

北京东城区2010—2011学年度第二学期高三综合练习（一）数学试题（理科）本试卷分第I 卷和第II 卷两部分，考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷（选择题，共40分）一、本大题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

1．“2x >”是“24x >”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件2．已知数列{}n a 为等差数列，且1234562,13,a a a a a a =+=++则等于（ ） A ．40 B ．42 C ．43 D ．453．已知函数对任意的x R ∈有f(x)+f(-x)=0,且当0,()ln(1)x f x x >=+时，则函数()f x 的图象大致为（ ）4．已知平面上不重合的四点P ，A ，B ，C 满足0,PA PB PC AB AC mAP ++=+=且，那么实数m 的值为（ ） A ．2 B ．3 C ．4D ．55．若右边的程序框图输出的S 是126，则条件①可为（ ）A ．5n ≤B ．6n ≤C ．7n ≤D ．8n ≤6．已知1(,),tan(),sin cos 247ππαπααα∈+=+那么的值 为 （ ）A ．15- B ．75 C ．—75 D ．34 7．已知函数131()()2x f x x =-，那么在下列区间中含有函数 ()f x 零点的是 （ ）A ．1(0,)3 B ．11(,)32 C ．()32,21 D ．⎪⎭⎫ ⎝⎛1,32 8．空间点到平面的距离定义如下：过空间一点作平面的垂线，这点和垂足之间的距离叫做这个点到这个平面的距离，平面,,αβγ两两互相垂直，点A α∈，点A 到平面,βγ的距离都是3，点P 是α上的动点，且满足P 到β的距离是P 到点A 距离的2倍，则点P 到平面γ的距离的最小值为（ ）A ．3BC ．3+D ．6 第Ⅱ卷（共110分）二、填空题：本大题共6小题，每小题5分，共30分。