利用定积分求曲线围成的面积

计算由曲线 y 2 = 2 x 和直线 y = x − 4 所围
成的图形的面积. 成的图形的面积
解 两曲线的交点
y = x−4
y2 = 2x y = x−4
⇒ ( 2,−2), (8,4).
y2 = 2 x
选 y 为积分变量
y ∈ [−2, 4] −
A = ∫ dA = 18.
−2 4
y2 dA = y + 4 − dy 2
0 x
x
x
两边同时对 x 求导
3 f ( x ) = 2 y + 2 xy ′ ⇒ 2 x y ′ = y
积分得 y = cx ,
2
9 因为曲线 y = f ( x ) 过点 ( 2 , 3 ) ⇒ c = 2
9 ∴ y = x, 2
2
因为 f ( x ) 为单调函数
3 所以所求曲线为 y = 2x. 2
a
b
例：曲线 y = x ( x − 1)( 2 − x )与 x轴所围图形的面积可表 为： A) − ∫ x ( x − 1)( 2 − x )dx ;
0 2
B ) ∫ x ( x − 1)( 2 − x )dx − ∫ x ( x − 1)( 2 − x )dx ;
0 1
1
2
C ) − ∫ x ( x − 1)( 2 − x )dx + ∫ x ( x − 1)( 2 − x )dx ;
6 曲线 y = x 2 与它两条相互垂直的切线所围成平面图 形的面积 S ，其中一条切线与曲线相切于点 A( a , a 2 ) ， a > 0 ，则当 a = __时，面积 S 最小 . __时
二、求由下列各曲线所围成的图形的面积： 求由下列各曲线所围成的图形的面积： 1 1、 y = 与直线 y = x 及 x = 2 ； x 2、 y = x 2 与直线 y = x 及 y = 2 x ； 3、 r = 2a ( 2 + cosθ ) ； 4 、 摆线 x = a( t − sin t ) , y = a (1 − cos t ) (0 ≤ t ≤ 2π ) 及 x 轴； 的公共部分； 5、 r = 3 cosθ 及 r = 1 + cosθ 的公共部分； 6、笛卡尔叶形线 x 3 + y 3 + 3axy .

积分学中的面积与弧长在数学领域中，积分学是一个重要的分支，其涉及到计算曲线下面的面积以及曲线的弧长。

在本文中，我们将探讨积分学中的面积与弧长的相关概念和计算方法。

一、面积计算在积分学中，我们可以利用定积分的概念来计算曲线下面的面积。

定积分的符号表示为∫，代表某一区间上函数曲线下的面积。

具体而言，在一维情况下，我们可以通过积分计算直线与坐标轴所夹的曲线下的面积。

以一个简单的例子来说明，假设我们要计算函数f(x)在区间[a, b]上的面积，其中f(x)是一个连续函数。

我们可以将[a, b]分成n个小区间，每个小区间的长度为Δx，然后选择每个小区间上的一个代表点xi。

对于每个小区间，我们可以计算出f(xi)与Δx的乘积，得到该小区间上的面积，然后将所有小区间上的面积相加即可。

当我们将n趋近于无穷大时，这个近似的和将会趋近于实际的曲线下面的面积。

而对于二维情况，我们可以通过对平面上的曲线进行积分来计算曲线所围成的区域的面积。

同样地，我们可以将曲线所围成的区域分成无穷多个小区域，然后通过计算每个小区域的面积，最后将所有小区域的面积相加来得到曲线围成的区域的面积。

二、弧长计算除了计算面积，积分学也可以用来计算曲线的弧长。

在数学中，曲线的弧长指的是曲线的长度。

在实际应用中，计算曲线的弧长在几何学、物理学等领域中都有着广泛的应用。

同样地，我们可以利用定积分的概念来计算曲线的弧长。

在一维情况下，假设我们有一个曲线y = f(x)，其中f(x)是一个连续函数。

我们可以将曲线所在的区间[a, b]分成n个小区间，每个小区间的长度为Δx。

然后，用勾股定理计算出每个小区间的弦长，并将这些弦长相加，即可得到曲线在区间[a, b]上的弧长的近似值。

当我们将n趋近于无穷大时，这个近似值将会趋近于曲线的实际弧长。

值得注意的是，计算弧长时所使用的公式与曲线的参数方程和极坐标方程有关。

对于参数方程，我们需要分别计算x和y的导数，然后再套入弧长的积分公式中进行计算。

利用定积分求曲线围成的面积
定积分是数学中一种重要的积分计算方法，用于求解两变量t和y之间函数关系的积分。

它是一种对曲线积分测量技术，通常用于求曲线所围成的面积。

下面介绍定积分求曲
线围成的面积的原理，以及如何运用定积分求解。

首先，求曲线所围成的面积，要求先将曲线分解为多个小矩形，这就是定积分技术的
基础。

定积分技术可以用原函数曲线在一个区间内离散对应的多个矩形累加得到该区间内
的整个积分值，其具体流程如下：
1. 首先确定积分区间，确定积分上下限，通常记做a和b；
2. 确定在积分区间中拆分的点数，也就是将积分区间拆分成多少子区间，其记号为n；
3. 经过上面的步骤后，就可以确定出定积分的“积分步长”h=（b-a）/ n；
4. 接下来根据所给函数，计算一下积分步长h对应的函数值，我们将这个值记为Fi，i为1,2,...,n，F1为a点处的函数值，F2为a+h点处的函数值，以此类推，Fn为b点处的函数值；
5. 通过上面计算出所有矩形的面积，把它们累加起来，就可以得到整个曲线所围成
的面积；
6. 如果矩形面积很小，也就是说n足够大，则积分值基本已经接近其实际值；
7. 再把整个曲线所围成的面积减去各个子矩形与曲线实际接触处的总面积，也就是
被曲线分割的矩形的形面积，就可以得到最终的积分结果了。

上面叙述的是定积分求曲线围成的面积的原理，要实际操作运用定积分求解，还需要
根据实际情况进行处理。

在实际应用中，需要特别注意函数在曲线上断点处不可能出现悬
挂断层，以及曲线上拐点处的积分计算。

只有在这些要点上仔细处理，定积分求曲线围成
的面积才可行。

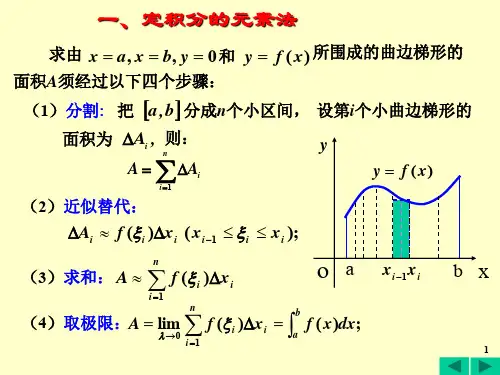
利用定积分求曲线围成的面积12.9 利用定积分求曲线围成的面积武汉外国语学校 汪家硕一．复习回顾：1.定积分的几何意义：当()0f x ≥时，积分()ba f x dx ⎰在几何上表示由()y f x =、x a =、xb =与x 轴所围成的曲边梯形的面积。

当()0f x ≤时，由()y f x =、x a =、x b =与x 轴所围成的曲边梯形位于x 轴的下方。

2.牛顿—莱布尼茨公式定理（微积分基本定理）如果()f x 是区间[,]a b 上的连续函数，并且'()()F x f x =，则()()()ba f x dx Fb F a =-⎰二．曲线围成的面积1.设f 和g 是区间[,]a b 上的连续函数且对任意的[,]x a b ∈有()()f x g x ≥，则直线x a =和直线x b =以及曲线间围成的面积可以表示为：()()()()b b ba a a f x dx g x dx f x g x dx -=-⎰⎰⎰例1.求抛物线2y x =和直线2y x =所围成的区域面积。

⎰b a f (x )dx =⎰c a f (x )dx +⎰b c f (x )dx 。

解：先求出P 点坐标。

解方程组22y x y x⎧=⎨=⎩ ⇒ 02x x =⎧⎨=⎩ ∴ P 点的坐标是(2,4)。

所求的面积= 22322008424333x x x dx x ⎡⎤-=-=-=⎢⎥⎣⎦⎰ 例1例2．计算曲线21y x =+和24y x =-，以及直线1x =和1x =-所围成的区域面积。

解：所求面积=11132221112144(1)32333x x x dx x dx x ---⎡⎤--+=-=-=⎢⎥⎣⎦⎰⎰例22.前面的例题都是一个曲线总在另外一个曲线的上方，如果它们交叉会是什么结果？考虑区间112233[,],[,],[,],[,]a c c c c c c b ，阴影部分面积可以表示为：123123()()()()()()()()c c c ba c c c f x g x dx g x f x dx f x g x dx g x f x dx -+-+-+-⎰⎰⎰⎰例3：求3()f x x =和()g x x =所围成的封闭区域面积。

利用定积分求曲线围成的面积This manuscript was revised on November 28, 2020利用定积分求曲线围成的面积武汉外国语学校 汪家硕一．复习回顾：1.定积分的几何意义：当()0f x ≥时，积分()ba f x dx ⎰在几何上表示由()y f x =、x a =、xb =与x 轴所围成的曲边梯形的面积。

当()0f x ≤时，由()y f x =、x a =、x b =与x 轴所围成的曲边梯形位于x 轴的下方。

2.牛顿—莱布尼茨公式定理（微积分基本定理）如果()f x 是区间[,]a b 上的连续函数，并且'()()F x f x =，则二．曲线围成的面积1.设f 和g 是区间[,]a b 上的连续函数且对任意的[,]x a b ∈有()()f x g x ≥，则直线x a =和直线x b =以及曲线间围成的面积可以表示为：()()()()bb ba a a f x dx g x dx f x g x dx -=-⎰⎰⎰ 例1.求抛物线2y x =和直线2y x =所围成的区域面积。

解：先求出P 点坐标。

解方程组22y x y x⎧=⎨=⎩ ⇒ 02x x =⎧⎨=⎩ ∴ P 点的坐标是(2,4)。

所求的面积= 22322008424333x x x dx x ⎡⎤-=-=-=⎢⎥⎣⎦⎰ 例1 例2．计算曲线21y x =+和24y x =-，以及直线1x =和1x =-所围成的区域面积。

解：所求面积=例22.前面的例题都是一个曲线总在另外一个曲线的上方，如果它们交叉会是什么结果考虑区间112233[,],[,],[,],[,]a c c c c c c b ，阴影部分面积可以表示为：例3：求3()f x x =和()g x x =所围成的封闭区域面积。

解：当()()=时图像的交点，f xg x即332=⇒-=⇒-=x x x x x x0(1)0例3 例4：求阴影部分的面积。

一、 填空题： 1、由曲线 y e x , y e 及 y 轴所围成平面区域的面积 是______________ . 2、由曲线 y 3 x 2 及直线 y 2 x 所围成平面区域的 面积是_____ . 3、由 曲 线 y x 1 x 2 , y 1 , x 1 , x 1 所 围 成平面区域的面积是_______ . 4 、计算 y 2 2 x 与 y x 4 所围的区域面积时，选用 ____作变量较为简捷 . 5 、由曲线 y e x , y e x 与直线x 1 所围成平面区 域的面积是_________ .

r ( )
d
o 1 面积元素 dA [ ( )]2 d 2 1 曲边扇形的面积 A [ ( )]2 d .

x
2
例 4
求双纽线 a cos 2 所围平面图形
2 2
的面积.
解 由对称性知总面积=4倍第 一象限部分面积
y x
A 4 A1
在(0,1) 内的一条切线, 使它与
两坐标轴和抛物线所围图形的面积最小.
B M
它与 x , y 轴的交点分别为
A
所指面积
得[ 0 , 1] 上的唯一驻点
B M
A
且为最小点 . 故所求切线为
x (t ) 如果曲边梯形的曲边为参数方程 y (t )
曲边梯形的面积
A ( t ) ( t )dt .
练习题答案
32 一、1、1； 2、 ； 3、2； 3 1 1 y e 2 4、 ； 5、 ； 6、 . e 2 3 7 2 a 二、1、 ln 2 ； 2、 ； 3、 ； 2 6 5 3 2 2 3 a 4、 ； 5、 ； 6、 a . 2 4 9 e 8 2 三、 . 四、 . 五、 a . 4 2 3

y2 2
4


y3
4

4y 2

6
2
18
8
注：如果取x为积分变量
X型 在 0,8 上任取小区间x, x dx,
则 dA 2 x1xdx

A

8
0
2 x
y穿出


1 x
y穿入
dx
y
dA
o (2,2)
(8,4)
以 f ( x)dx作为 A的近似值。
即： A f ( x)dx
f ( x)dx 叫做面积元素, 记为
dA f ( x)dx
Oa
y f (x)
A
dx
x x dx
b
x
b
（3）写出A的积分表达式，即：A f ( x)dx a
3
一般地，如果某一实际问题中的所求量 U符合下列条件：
以极点O为圆心，以 a为半径的的圆的极坐标方程: r a.
P(r, )
P(r, )
r

O
(a,0) x O (a,0)
x
P(r, )

3
3
O
x
以点(a,0) 为圆心，以 a 为半径的的圆的极坐标方程 r 2a cos
过极点O，且与极轴的夹角为 的直线方程 .
（1）U是与一个变量x的变化区间[a，b]有关的量； （2）U对于区间[a，b]具有可加性；
（3）部分量
U
的近似值可表为
i
f i xi
那么这个量就
可以用积分来表示。
具体步骤是：
（1）确定积分变量，和它的变化区间[a,b]； （2）写出积分元素

12.9利用定积分求曲线围成的面积
武汉外国语学校
汪家硕
•复习回顾:
b 1.定积分的几何意义：当f(x)_O 时，积分 f(x)dx 在几何上表示由y = f(x)、x = a 、x =b _a 与x 轴所围成的曲边梯形的面积。

当f(x)空0时，由y 二f(x)、x 二a 、x 二b 与x 轴所围成的曲边梯形位于x 轴的下方。

2.牛顿一莱布尼茨公式
定理(微积分基本定理)如果f (x)是区间［a, b ］上的连续函数，并且F (x)= f (x)，则 二•曲线围成的面积
1.设f 和g 是区间［a,b ］上的连续函数且对任意的［a,b ］有f(x) —g(x)，则直线x = a 和直
线x =b 以及曲线间围成的面积可以表示为：
b b b
J f(x)dx —a g(x)dx=J f(x)—g(x)dx a a a 例1求抛物线y =x 2和直线y =2x 所围成的区域面积。

例2.计算曲线y =X 2 • 1和y =4 -X 2，以及直线x =1和x - -
1所围成的区域面积
解：所求面积=
例2
解：先求出P 点坐标 解方程组 P 点的坐标是(2,4) 所求的面积=
2x -x 2dx 二 x 2 0 - A
0 a b
2.前面的例题都是一个曲线总在另外一个曲线的上方,
它们交叉会是什么结果？
考虑区间［a’CiHcitLGqHob］，阴影部分面积可以表示为: 例3:求f(x) =x3和g(x)二x所围成的圭寸闭区域面积
解：当f(x)=g(x)时图像的交点，
即x3 = x 二f - x 0 : (x 2x 1) £
例4:求阴影部分的面积
练习：
1.求阴影部分面积例3例4。

用定积分求面积的两个常用公式浙江 曾经求平面图形围成的面积是定积分重要应用之一，下面介绍求面积的两个常用公式及其应用．一、两个常用公式公式一：由连续曲线y ＝f (x ),直线x ＝a ，x ＝b 与y ＝0所围成的曲边梯形的面积A 为A ＝|()|b af x dx ⎰．特别地,⑴当f (x )≥0时(如图1)，A ＝()baf x dx ⎰;⑵当f (x ）≤0时（如图2),A ＝－()b af x dx ⎰；⑶当f (x )有正有负时(如图3），A ＝()c af x dx ⎰－()b cf x dx ⎰．公式二：由连续曲线y ＝f （x )，y ＝g (x ），f (x )≥g (x ）及直线x ＝a ,x ＝b 所围成的图形（如图4)的面积A 为A ＝[()()]b af xg x dx -⎰．二、应用举例例1 由y ＝x 3，x ＝0,x ＝2，y ＝0围成的图形面积．分析:先画出图象，利用公式1转化为定积分问题即可解决．1图2图解：⑴如图1，由公式1，得S ＝230x dx⎰＝42440111|204444x =⨯-⨯=． 评注：注意定积分与利用定积分计算曲线围成图形的面积区别．定积分是一种积分和的极限,可为正,也可为负或零,而平面图形的面积在一般意义上总为正．一般情况下，借助定积分分别求出每一部分曲边梯形的面积,然后将它们加在一起．例2 ⑴由曲线y ＝x 2，y 2＝x 所围成图形的面积．⑵由y ＝14x 2－1，y ＝12x ，y ＝34x 在第一象限所围成图形的面积．分析：先画图象找出范围，利用公式2，用积分表示，再求积分．解：⑴ 如图2，所求面积为阴影部分．解方程组22y xy x ⎧=⎪⎨=⎪⎩，得交点(0，0)，(1，1）,由公式2，得S＝120)x dx ⎰＝331202211()|33333x x -=-=． ⑵如图3，解方程组211412y x y x⎧=-⎪⎪⎨⎪=⎪⎩和211434y x y x ⎧=-⎪⎪⎨⎪=⎪⎩，得x ＝0，x ＝1负的舍去),x ＝4．由公式2，得图形面积S＝1031()42x dx -⎰＋42111[(1)]42x x dx --⎰3图216-=．。

(3) 生产多少单位产品才能获得最大利润；
(4) 最大利润是多少?
解：(1)
C( x) C(0)
x
C(t)dt 200
x
(16 0.002t)dt
0
0
16x 0.001x2 200
(2) L( x) R( x) C( x) px C( x) (20 0.001x)x (16x 0.001x2 200) 0.002x2 4x 200
S
2

y

4

2
dy
18.
选x为积分变量
2
8
S 0 2x ( 2x ) dx 2 ( 2x ( x 4))dx 18.
例：求由曲线 y 1 与y x, x 2 所围面积。
x
解： 画草图，
y y 1
x
2
1
S

1
(x

)dx x
c
d
b
S S1 S2 S3
f ( x)dx
a
c
f ( x)dx
d
f ( x)dx
b
a | f ( x) | dx
由y f ( x), x a, x b及x轴所围图形的面积为
b
S a | f ( x) | dx
一条曲线（积分变量为y）
y
d
x (y)
y
d
y
d
x (y) e
c
c
c
O
x
O
x
O
x
(1) ( y) 0 (2) ( y) 0

习题5.61. 求下列曲线所围成的图形的面积：(1) 1y x=与直线y x =及2x =； (2) 22x y y =-与直线2y x =+；(3) 1=与两坐标轴；(4) 2236x y y +=与直线y x =(两部分都要计算)；(5) ln y x =与直线ln y a =，ln y b =(0b a >>)及y 轴；(6) |ln |y x =与直线1e x =，e x =及x 轴. 2. 求下列图形的面积：(1) 抛物线22y px =(0p >)及其在点,2p p ⎛⎫⎪⎝⎭处的法线所围成的图形； (2) 曲线e x y =与通过坐标原点的切线及y 轴所围成的图形.3. 求抛物线21y x =-+在(0,1)内的一条切线，使得它与两坐标轴及该抛物线所围成的图形的面积最小.4. 求下列曲线所围成的图形的面积： (1) 星形线33cos ,sin ;x a t y a t ⎧=⎨=⎩ (2) 心脏线(2cos cos 2),(2sin sin 2).x a t t y a t t =-⎧⎨=-⎩5. 设P 为曲线2cos ,2sin x t y t =⎧⎨=⎩ π02t ⎛⎫≤≤ ⎪⎝⎭上的一点，O 为坐标原点，记曲线与直线OP 及x 轴所围成的图形的面积为S .(1) 把y 表示成x 的函数，并求面积()S S x =的表达式；(2) 把S 表示成t 的函数()S t ，并求d d S t取得最大值时点P 的坐标. 6. 求下列曲线所围成的图形的面积：(1) 心脏线2(1cos )r a θ=- (0a >)；(2) 双纽线22cos 2r a θ=.7. 求下列曲线所围成的图形的公共部分的面积：(1) 3cos r θ=及1cos r θ=+；(2) r θ=及2cos 2r θ=；(3) 22cos 2r θ=，2cos r θ=及1r =.8. 在双纽线24cos 2r θ=位于第一象限部分上求一点M ，使得坐标原点O 与点M 的连线OM 将双纽线所围成的位于第一象限部分的图形分为面积相等的两部分.9. 求下列各立体的体积：(1) 以椭圆域22221x y a b+≤ (0a b >>)为底面，且垂直于长轴的截面都是等边三角形的立体；(2) 由曲面222e x y z -+=与平面0x =，1x =所围成的立体.10. 求下列各旋转体的体积：(1) 抛物线2y x =与28y x =所围成的图形分别绕x 轴、y 轴旋转所得的旋转体；(2) 曲线sin y x =，cos y x = π02t ⎛⎫≤≤⎪⎝⎭与直线π2x =，0x =所围成的图形绕x 轴旋转所得的旋转体； (3) 摆线(sin )(0)(1cos )x a t t a y a t =-⎧>⎨=-⎩的第一拱(02π)t ≤≤与x 轴所围成的图形绕直线2y a =旋转所得的旋转体.11. 用“薄壳法”求下列各旋转体的体积：(1) 由曲线2(1)y x x =-与x 轴所围成的图形绕y 轴旋转所得的旋转体；(2) 由抛物线22y x x =-与直线y x =及x 轴所围成的图形绕y 轴旋转所得的旋转体.12. 求下列各旋转体的体积：(1) 抛物线y =(1,0)的切线及x 轴所围成的图形绕x 轴旋转所得的旋转体；(2) 抛物线y =(2,4)处的法线及x 轴所围成的图形绕x 轴旋转所得的旋转体.13. 设抛物线2y ax = (0,0a x >≥)与21y x =-的交点为A ，过坐标原点O 与点A 的直线与抛物线2y ax =围成一平面图形. 问a 为何值时，该图形绕x 轴旋转所得的旋转体体积最大？并求此最大体积.14. 求下列各旋转面的面积：(1) 立方抛物线3y x =介于0x =与1x =之间的一段弧绕x 轴旋转所得的旋转面；(2) 星形线222333x y a +=绕x 轴旋转所得的旋转面.15. 求抛物线y =x 轴所围成的图形绕x 轴旋转所得的旋转体的表面积.16. 计算下列各弧长：(1) 曲线2ln 42x x y =-相应于1e x ≤≤的一段弧； (2) 曲线ln(cos )y x =上从0x =到π4x =的一段弧；(3) 曲线y t =⎰的全长；(4) 曲线arctan x t =，2ln(1)2t y +=相应于01t ≤≤的一段弧； (5) 对数螺线2e r θ=上从0θ=到2πθ=的一段弧；(6) 曲线112r r θ⎛⎫=+ ⎪⎝⎭相应于13θ≤≤的一段弧. 17. 在摆线(sin )(0)(1cos )x a t t a y a t =-⎧>⎨=-⎩上求分其第一拱成1:3的点的坐标.18. 若1kg 的力能使弹簧伸长1cm ，现在要使这弹簧伸长10cm ，问需要做多少功？19. 用铁锤将一铁钉击入木板，设木板对铁钉的阻力与铁钉击入木板的深度成正比. 在击第一次时，将铁钉击入木板1cm. 如果铁锤每次打击铁钉所做的功相等，问铁锤击第二次时，铁钉又被击入多少？20. 一蒸汽锅是旋转抛物面形状，开口朝上，口半径为R ，高为H ，其中盛满了密度为ρ的液体，问从锅中将液体全部抽出需做多少功？21. 有一水槽，其横截面为等腰梯形，两底的长分别为0.8m 和0.4m ，高为0.2m ，较长的底在上. 当盛满水时，求横截面上一侧所受的压力.22. 边长为a 和b 的矩形薄板(a b >)，与液面成α角斜沉于密度为ρ的液体内，长边平行于液面而位于深h 处. 试求薄板每面所受的压力.23. 一根长为l ，质量为M 的均匀细直棒，在棒的延长线上距棒右端点a 单位处有一质量为m 的质点，若将该质点沿棒的延长线从a 处移至b 处(b a >)，试求克服引力所做的功.24. 求一质量为M ，半径为R 的均匀半圆弧对位于其中心的质量为m 的质点的引力.。

利用积分求面积问题在数学中，积分是一种重要的数学工具，可以用来求解各种问题，包括求面积问题。

利用积分求面积问题是一种常见的应用，它可以帮助我们计算曲线与坐标轴之间的面积。

本文将介绍如何利用积分来解决这类问题。

首先，我们来看一个简单的例子。

假设有一条曲线y=f(x)，我们想要求解该曲线与x轴之间的面积。

为了方便计算，我们将曲线分成无数个小矩形，每个小矩形的宽度为Δx，高度为f(x)。

那么每个小矩形的面积可以表示为ΔA=f(x)Δx。

为了求解整个曲线与x轴之间的面积，我们需要将所有小矩形的面积相加。

由于曲线是连续的，我们可以将Δx无限地趋近于0，这样就可以得到一个无穷小的矩形。

我们可以用积分来表示这个过程，即∫f(x)dx。

利用积分的性质，我们可以将上述积分转化为一个定积分，即∫a^b f(x)dx，其中a和b分别表示曲线与x轴的交点。

这样，我们就可以通过求解定积分来得到曲线与x轴之间的面积。

接下来，我们来看一个具体的例子。

假设有一条曲线y=x^2，我们想要求解该曲线与x轴之间的面积。

首先，我们需要找到曲线与x轴的交点。

当y=0时，即x^2=0，解得x=0。

因此，曲线与x轴的交点为(0,0)。

然后，我们可以利用定积分来求解面积。

根据上述公式，我们有∫0^1 x^2dx。

通过求解这个定积分，我们可以得到曲线与x轴之间的面积。

利用积分的性质，我们可以将上述定积分转化为一个不定积分，即∫x^2dx。

通过求解这个不定积分，我们可以得到曲线与x轴之间的面积。

对于这个不定积分，我们可以使用积分的基本公式来求解。

根据积分的基本公式，我们有∫x^2dx=(1/3)x^3+C，其中C为常数。

将上述结果代入定积分的公式，我们有∫0^1 x^2dx=(1/3)(1^3-0^3)=1/3。

因此，曲线y=x^2与x轴之间的面积为1/3。

通过这个例子，我们可以看到利用积分求解面积问题的基本思路。

首先，我们需要找到曲线与x轴的交点。

数学微积分定积分公式整理微积分是数学中的重要分支，它主要研究函数的变化率和积分运算。

在微积分中，定积分是积分的一种形式，它用来求解曲线与坐标轴所围成的面积或曲线的长度。

定积分公式是定积分计算的基础，下面我将对一些常用的定积分公式进行整理和归纳。

一、基本的定积分公式1. 幂函数的定积分公式：∫x^n dx = 1/(n+1) * x^(n+1) + C，其中C为常数。

这个公式适用于任意实数n，其中n不等于-1。

2. 指数函数的定积分公式：∫e^x dx = e^x + C，其中C为常数。

指数函数e^x的定积分就是它自身再加上一个常数C。

3. 三角函数的定积分公式：∫sin x dx = -cos x + C∫cos x dx = sin x + C这两个公式是三角函数的定积分公式，其中C为常数。

4. 常数函数的定积分公式：∫k dx = kx + C，其中k为常数。

这个公式表示常数函数的定积分是它自身再乘以x再加上一个常数C。

二、定积分的性质1. 定积分的线性性质：∫[a*f(x) + b*g(x)] dx = a*∫f(x) dx + b*∫g(x) dx这个公式表示定积分具有线性性质，可以将函数的线性组合的积分转化为各个函数的积分之和。

2. 定积分的区间可加性：∫[a, b] f(x) dx + ∫[b, c] f(x) dx = ∫[a, c] f(x) dx这个公式表示定积分在不同区间上的结果可以进行相加，得到整个区间的定积分。

三、一些常见的定积分公式1. 正弦函数的定积分公式：∫sin^2 x dx = (1/2) * x - (1/4) * sin 2x + C∫sin^3 x dx = -(1/3) * cos^3 x + C这两个公式可用于计算正弦函数的定积分。

2. 余弦函数的定积分公式：∫cos^2 x dx = (1/2) * x + (1/4) * sin 2x + C∫cos^3 x dx = (1/3) * sin^3 x + C这两个公式可用于计算余弦函数的定积分。

定积分求面积平面图形的面积有两点需要注意，一个是选择用极坐标计算面积还是选择用极坐标系计算面积，一个是在计算面积是应该注意正负，定积分是有正负的，但是面积都是正的，在理解了定积分的含义之后，要明白计算面积时要加绝对值，或者在负的定积分前加负号，保证计算出来的面积是正的。

定积分在几何上的意义是曲线围成的面积，那么它只能求面积吗?它的应用可广泛了，可以这样说，我们都有一门课叫大学物理，其实大学物理跟高中物理相比在知识点上并没有增加多少，只是用微积分的方法解决了一些连续性变化的物理问题而已。

很多同学觉得大学物理难学，那一定是你没有领会微积分的真谛，也就是不会使用微积分解决实际问题。

用定积分求平面图形面积的关键是根据题意准确确定平面图形的边界，并根据边界将面积正确的写成积分形式。

用定积分求弧长问题难点在于曲线方程的直角坐标系形式与极坐标系形式之间的转换，以及对这些变换的理解，然后就是对三角函数类定积分的熟练计算，很多时候不能“蛮算”要“巧算”。

很多同学觉得这是很简单的事情，而不以为然，认为这种题目很简单没有必要浪费时间去做，可是到了考试时候真正出现这种题目，又有几个人能用很短的时间把题目做正确？确定边界问题咋一看很简单——不就是初中数学的内容吗？但是解题需要的是熟练，而熟练必然建立在多练习多总结的基础上。

此外用定积分求面积问题积累的经验在后面多重积分的应用问题中也非常有用，求曲线弧长积累的经验在后面曲线曲面积分计算中也很有用。

很多同学之所以觉得曲线曲面积分、多重积分很难是因为定积分学的不够扎实。

如果我们在一维的数学思维训练够了，那么学习更高维的数学就不再是难事。

见到题目都觉得简单，都不想去动手做，最终必然是什么都不会。

所以希望同学们从基础题目做起，千万不要眼高手低——天下难事必作于易。

阿基米德螺旋线0到π的一段弧与极轴所围成的图形面积的定积分式子s阿基米德螺旋线（Archimedes spiral）是以极轴上的点作为原点的螺旋线。

它的定积分式子s，即求出极轴和该段弧围成的图形面积。

首先，来了解什么是阿基米德螺旋线。

阿基米德螺旋线是经典几何中定义的螺旋线。

它由一系列由内向外旋转的曲线构成，此类曲线中形状和大小是连续变化的，而极坐标只在极轴上矢量方向是连续变化的。

这种坐标系由一个极轴和轴上的点（极点）和另一点（半径点）构成。

极轴是由它的极点和与之相连的半径线构成的，而轴上的点代表着曲线的变化，每一次连接极点和半径点形成的弧线都是一个阿基米德螺旋线。

由于阿基米德螺旋线是由极轴和形成它的弧构成，因此求它们之间图形面积的定积分式子s便可以得到。

所谓定积分式子s，即用它来表示求出极轴和与它构成的弧形成的图形的面积的定积分式子。

令r=r0e^(αθ)（r0为极轴弧度），那么极轴和形成它的弧线围成的图形的面积的定积分式子就是：s=∫_0^π{r^2 dθ}=∫_0^π{r_0^2e^（2αθ）dθ}=∫_0^π{r_0^2(2αθ+1)e^（αθ）dθ}=r_0^2（2απ+π）该定积分式子是求出极轴和构成它的旋转弧围成图形的面积。

求出该面积，首先要计算它的定积分式子，即s=r_0^2（2απ+π）因此，有了定积分式子，就可以求出极轴和构成它的旋转弧围成图形的面积。

总之，阿基米德螺旋线是经典几何中定义的螺旋线，当求出极轴和构成它的旋转弧围成图形的面积的定积分式子时，可以将它写成：s=r_0^2（2απ+π）定积分式子以及它的计算过程可以为我们更好的理解阿基米德螺旋线提供帮助，为我们在几何中更好的运用提供了参考。

定积分的概念和性质公式定积分是微积分的重要概念之一，用于计算曲线下面的面积或者曲线围成的面积，以及求解一些几何体的体积。

本文将介绍定积分的概念、性质以及相关的公式。

一、定积分的概念在数学中，定积分可以看作是无穷小量的累加，它的计算结果是一个数值。

定积分的概念可以通过求解函数和坐标轴之间的面积来解释。

设对于连续函数y=f(x)在区间[a,b]上，我们将它与x轴围成的平面区域分割成多个无穷小的矩形，其宽度为Δx。

我们分别计算每个矩形的面积，将这些面积相加，然后取极限得到的结果就是函数f(x)在区间[a,b]上的定积分。

表示为：∫[a,b]f(x) dx = limΔx→0 Σf(x_i)Δx其中，Σ表示求和，f(x_i)表示在每个小矩形的高度，Δx表示每个小矩形的宽度。

二、定积分的性质1.线性性质：设函数f(x)和g(x)在区间[a,b]上可积，k为常数，则有：∫[a,b](f(x)+g(x))dx = ∫[a,b]f(x)dx + ∫[a,b]g(x)dx∫[a,b]k*f(x)dx = k*∫[a,b]f(x)dx2.区间可加性质：设函数f(x)在区间[a,b]和[b,c]上可积，则：∫[a,c]f(x)dx = ∫[a,b]f(x)dx + ∫[b,c]f(x)dx3.估值性质：设f(x)在区间[a,b]上非负可积，c是[a,b]上的任意一点，则有：f(c)*(b-a) ≤ ∫[a,b]f(x)dx ≤ M*(b-a)其中，M为f(x)在[a,b]上的最大值。

4.小于等于零性质：设函数f(x)在区间[a,b]上非负可积并且在[a,b]上恒大于等于0，则有：∫[a,b]f(x)dx ≤ 0 当且仅当f(x)恒为零。

5.平均值定理：设函数f(x)在区间[a,b]上可积，则存在一个点c使得：∫[a,b]f(x)dx = f(c)*(b-a)三、定积分的计算公式1.基本积分法则：∫k dx = kx + C （k为常数）∫x^n dx = (x^(n+1))/(n+1) + C （n≠-1）2.叠加性质：∫[a,b]f(x)dx = ∫[a,c]f(x)dx + ∫[c,b]f(x)dx3.替换法则：设F(x)在区间[a,b]上可导，f(g(x))g'(x)在区间[g(a),g(b)]上连续，则有：∫[a,b]f(g(x))g'(x)dx = ∫[g(a),g(b)]f(u)du ，其中u=g(x)4.分部积分法则：设u(x)和v(x)是具有连续导数的函数，则有：∫u(x)v'(x)dx = u(x)v(x) - ∫u'(x)v(x)dx5.换元法则：设F(x)在区间[a,b]上可导，f(u)u'(x)在区间[u(a),u(b)]上连续，则有：∫[a,b]f(u(x))u'(x)dx = ∫[u(a),u(b)]f(u)du6.常用积分表：∫sin(x)dx = -cos(x) + C∫cos(x)dx = sin(x) + C∫1/(1+x^2)dx = arctan(x) + C∫1/√(1-x^2)dx = arcsin(x) + C∫e^x dx = e^x + C∫ln(x) dx = xln(x)-x + C总结：定积分是微积分的关键概念之一，通过对函数和坐标轴之间的面积进行累加，计算结果为一个数值。