全微分的几何意义
- 格式：ppt
- 大小：178.50 KB
- 文档页数：2
下载文档原格式
合集下载
全微分及其应用
常见方法
求解无约束最优化问题的方法包括梯度下降法、 牛顿法、拟牛顿法等。
牛顿法
牛顿法是一种基于目标函数二阶导数的迭代算法 ，通过构造海森矩阵并求解线性方程组来逼近最 优解。
有约束最优化问题
01
有约束最优化问题
有约束最优化问题是在存在约束条件限制下，寻找满 足所有约束条件的参数的最优解。
02 分类 有约束最优化问题可以分为等式约束问题和不等式约 束问题。
极值点判断
全微分还可以用于判断函数的极值点。如果函数在某一点的导数等于0，则该点 可能是函数的极值点。
函数极值点的判断
极值点判断
全微分可以用于判断函数的极值点。如果函数在某一点的导数等于0，且该点的二阶导数大于0，则该点 是函数的极值点。
极值点类型判断
全微分还可以用于判断函数的极值点类型，如极大值点或极小值点。如果函数在某一点的二阶导数小于0， 则该点是极大值点；如果二阶导数大于0，则该点是极小值点。
全微分的几何意义
总结词
全微分在几何上表示函数图像在 某一点处的切线斜率。
详细描述
全微分可以理解为函数图像在某 一点处的切线的斜率，这个斜率 表示函数在该点处沿任一方向的 变化率。
全微分的性质
总结词
全微分具有线性性质、可加性、可乘性和链式法则等性质。
详细描述
全微分具有线性性质，即两个函数的和或差的微分等于它们各自微分的和或差；全微分具有可加性，即函数在两 点间的微分等于这两点间各自微分的和；全微分还具有可乘性和链式法则等性质，这些性质在求导和积分中有着 广泛的应用。
应用
全微分在几何上表示函数图像在某点处的切线斜率的变化 量。
全微分在优化、近似计算、泰勒级数展开等方面有广泛应 用。
复合函数的偏导数和全微分课件
复合函数的偏导数和全微 分课件
• 引言 • 复合函数的偏导数 • 复合函数的全微分 • 偏导数和全微分的应用 • 习题与解答
01
引言
课程背景
复合函数是高等数学中的重要概念， 它在解决实际问题中有着广泛的应用。
偏导数和全微分是复合函数分析中的 关键概念，对于理解复合函数的性质 和计算方法具有重要意义。
05
习题与解答
习题部分
计算复合函数f(u,v)的偏导数
给定u=u(x,y)和v=v(x,y)，求f对x和y的偏导数。
计算全微分
给定复合函数f(u,v)的全微分表达式，求f对u和v的全微分。
判断偏导数和全微分的关系
根据偏导数和全微分的定义，判断它们之间的关系。
答案与解析
计算复合函数f(u,v)的 偏导数
偏导数的符号表示
用"∂"表示偏导数，例如：f'x(x0, y0)表示函数f在点(x0, y0)处对x的偏导数。
复合函数的偏导数计算
链式法则
对于复合函数，如果外层函数是u(x, y) = f(g(x, y))，则其偏导数为∂u/∂x = ∂f/∂g * ∂g/∂x。
隐式函数求导
对于由方程F(x, y) = 0定义的隐式函数y， 其偏导数为∂y/∂x = -F'x / F'y。
曲线和曲面的切线问题
切线的定义
切线是曲线或曲面在某一点的邻近区域 内的一条直线。在数学上，切线是通过 曲线或曲面在该点的外法线向量定义的 。
VS
切线的求法
通过求曲线或曲面的偏导数，我们可以得 到曲线或曲面在该点的切线方向。在三维 空间中，切线可以用一个向量来表示，该 向量与曲线或曲面的外法线向量平行。
• 引言 • 复合函数的偏导数 • 复合函数的全微分 • 偏导数和全微分的应用 • 习题与解答
01
引言
课程背景
复合函数是高等数学中的重要概念， 它在解决实际问题中有着广泛的应用。
偏导数和全微分是复合函数分析中的 关键概念，对于理解复合函数的性质 和计算方法具有重要意义。
05
习题与解答
习题部分
计算复合函数f(u,v)的偏导数
给定u=u(x,y)和v=v(x,y)，求f对x和y的偏导数。
计算全微分
给定复合函数f(u,v)的全微分表达式，求f对u和v的全微分。
判断偏导数和全微分的关系
根据偏导数和全微分的定义，判断它们之间的关系。
答案与解析
计算复合函数f(u,v)的 偏导数
偏导数的符号表示
用"∂"表示偏导数，例如：f'x(x0, y0)表示函数f在点(x0, y0)处对x的偏导数。
复合函数的偏导数计算
链式法则
对于复合函数，如果外层函数是u(x, y) = f(g(x, y))，则其偏导数为∂u/∂x = ∂f/∂g * ∂g/∂x。
隐式函数求导
对于由方程F(x, y) = 0定义的隐式函数y， 其偏导数为∂y/∂x = -F'x / F'y。
曲线和曲面的切线问题
切线的定义
切线是曲线或曲面在某一点的邻近区域 内的一条直线。在数学上，切线是通过 曲线或曲面在该点的外法线向量定义的 。
VS
切线的求法
通过求曲线或曲面的偏导数，我们可以得 到曲线或曲面在该点的切线方向。在三维 空间中，切线可以用一个向量来表示，该 向量与曲线或曲面的外法线向量平行。
高等数学————微分
五、全微分在近似计算中的应用
( 1 ) z dz f x ( x0 , y0 )x f y ( x0 , y0 )y
例4 设一金属圆柱受压变形后，底面半径由原来的 20cm变到20.1cm，高由原来的40cm减少到39.5cm，求 该金属体体积变化的近似值。 解：设圆柱体的底面半径为r，高为h，体积为V 则有 V r 2 h 所以
2 2
u u u ( 2) du dx dy dz x y z 1 y yz ye yz dz dx ( cos ze )dy 2 2
u u u ( 3) du dx dy dz x y z
yzx
yz1
zx yz ln xdy yx yz ln xdz dx
N ( x0 x, y0 y, z0 z )
z =AN ：曲面立标的增量
z
z
B
过点M的切平面：
dz=AB : 切面立标的增量
z dz ( x y )
=AB+BN
z z0
dz
A
.
当x , y 很小时
0
z dz
x
P
y
y
Q
四、全微分的计算
可导 可微.
A f ( x0 ).
函数 y f ( x )在任意点 x的微分, 称为函数的 微分, 记作 dy或 df ( x ), 即 dy f ( x )x .
3、微分的几何意义
几何意义:(如图)
y
T N
o( x )
当y是曲线的纵 坐标增量时, dy 就是切线纵坐标 对应的增量.
z z dz x y x y
证明： 由函数 z f ( x , y ) 在点（x，y）处可微有
全微分的定义4版
z f ( x, y)
( x0 , y0 , z0 )
五、小结与思考 比 较
小
结
多元函数 ① 多元函数全微分的定义 ; 一元函数
偏导数连续 ② 多元函数全微分的求法 ; 重点 只要会求偏导数，就会求全微分！ 等价关系
③ 多元函数连续、可导、可微的关系 . 难点 可微 可偏导 可微 可导
思
考
( x ay )dx ydy 已知 2 ( x y) 连续 连续 是某函数的全微分，求a.
dy f ( x)dx
二、二元函数的全微分
由一元函数微分学中增量与微分的关系得
f ( x x , y ) f ( x , y ) f x ( x, y )x
f ( x , y y ) f ( x , y ) f y ( x , y ) y
二元函数 对x和对y的偏增量 二元函数 对x和对y的偏微分
x 0 y 0
lim f x ( x 1x, y y )=f x ( x, y )
从而有f x ( x 1x, y y )x =f x ( x, y )x 1x 其中1为x, y的函数,且当x 0, y 0时,1 0.
f ( x x) f ( x) f ( x x)x
上式两端除以x，当x 0并取极限，即得 f ( x +x, y ) f ( x, y ) z lim A，即 A, x 0 x x z 同理可证B= .故定理1得证. y
注意 一元函数在某点的导数存在 微分存在．
二元函数的各偏导数存在
全微分存在．
答案是否定的 !
x2 y 2 0 x2 y 2 0
可偏导
可微
xy 2 2 二元函数 f ( x, y ) x y 0
( x0 , y0 , z0 )
五、小结与思考 比 较
小
结
多元函数 ① 多元函数全微分的定义 ; 一元函数
偏导数连续 ② 多元函数全微分的求法 ; 重点 只要会求偏导数，就会求全微分！ 等价关系
③ 多元函数连续、可导、可微的关系 . 难点 可微 可偏导 可微 可导
思
考
( x ay )dx ydy 已知 2 ( x y) 连续 连续 是某函数的全微分，求a.
dy f ( x)dx
二、二元函数的全微分
由一元函数微分学中增量与微分的关系得
f ( x x , y ) f ( x , y ) f x ( x, y )x
f ( x , y y ) f ( x , y ) f y ( x , y ) y
二元函数 对x和对y的偏增量 二元函数 对x和对y的偏微分
x 0 y 0
lim f x ( x 1x, y y )=f x ( x, y )
从而有f x ( x 1x, y y )x =f x ( x, y )x 1x 其中1为x, y的函数,且当x 0, y 0时,1 0.
f ( x x) f ( x) f ( x x)x
上式两端除以x，当x 0并取极限，即得 f ( x +x, y ) f ( x, y ) z lim A，即 A, x 0 x x z 同理可证B= .故定理1得证. y
注意 一元函数在某点的导数存在 微分存在．
二元函数的各偏导数存在
全微分存在．
答案是否定的 !
x2 y 2 0 x2 y 2 0
可偏导
可微
xy 2 2 二元函数 f ( x, y ) x y 0
导数-微分-偏导数-偏微分-全微分
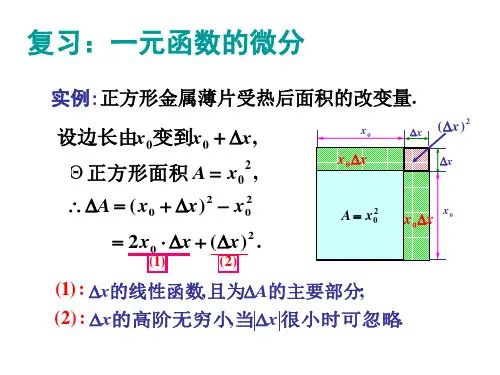
导数-微分-偏导数-偏微分-全微分在⼀些数学公式的推导中，常会遇到d / ∂ / δ \ Δ 等符号。
它们背后分别代表的数学含义？增量设变量u从它的⼀个初值u1变到终值u2，终值与初值的差u2−u1就叫做变量u的增量，记作 Δu，即Δu=u2−u1增量 Δu可以是正的，也可以是负的。
应该注意到：记号 Δu 并不表⽰某个量 Δ 与变量 u 的乘积，⽽是⼀个整体不可分割的记号。
举例：现在假定函数y=f(x) 在点x0的某⼀个邻域内是有定义的。
当⾃变量x在这个邻域内从x0变到x0+Δx时，函数值（或因变量）f(x) 相应地从f(x0) 变到f(x0+Δx)，因此，函数值（或因变量）f(x) 的对应增量为Δy=f(x0+Δx)−f(x0)习惯上也称 Δy为函数的增量。
由此，可以定义函数的连续性，如下：设函数y=f(x) 在点x0) 的某⼀个邻域内有定义，如果limΔx→0Δy=limΔx→0[f(x0+Δx)−f(x0)]=0，那么就称函数y=f(x) 在点x0连续。
导数导数的定义：设函数y=f(x) 在点x0的某个邻域内有定义，当⾃变量x在x0处取得增量 Δx（点x0+Δx仍在该邻域内）时，相应地，因变量取得增量 Δy=f(x0+Δx)−f(x0)；如果 Δy与 Δx之⽐当 Δx→0 时的极限存在，那么称函数y=f(x) 在点x0处可导，并称这个极限为函数y=f(x) 在点x0处的导数，记为f′(x) ，即f′(x)=limΔx→0ΔyΔx=limΔx→0f(x0+Δx)−f(x0)Δx,也可记作y′|x=x0，$$\frac{dy}{dx}|_{x = x_0}$ 或df(x)dx|x=x0。
可以看出，导数等于增量 Δy和增量 Δx⽐值的极限。
函数的微分微分的定义：设函数y=f(x) 在某区间内有定义，x0及x0+Δx在这个区间内，如果函数的增量Δy=f(x0+Δx)−f(x0)可表⽰为Δy=AΔx+o(Δx)其中，A是不依赖于 Δx的常数，那么，称函数y=f(x) 在点x0是可微的，⽽AΔx叫做函数y=f(x) 在点x0相应于⾃变量增量 Δx的微分，即dy=AΔx注：函数f(x) 在点x0可微的充要条件是函数f(x) 在点x0可导。
第六章3 全微分
1 cos y + (2 2
的全微分.
yz ) d y ze
练习： 练习：设
注意: 注意 x , y , z 具有 x 解: Q f (x,0,0) = 轮换对称性 3 + cos x 1 x ′ = ) ∴ f x (0,0,0) = ( 3 + cos x x = 0 4
1 f y (0,0,0) = f z (0,0,0) = 4 ∴d f (0,0,0) = f y (0,0,0) d x + f y (0,0,0) d y + f z (0,0,0) d z 1 = (d x + d y + d z) 4
(∆x)2 + (∆y)2 ∆x ∆y = 0 2 2 (∆x) + (∆y)
≠ o(ρ ) 因此,函数在点 (0,0) 不可微 .
定理2 定理 (充分条件) 若函数
的偏导数
在 (x, y) 连 , 则函数在该点可微分. 点 续 证：∆z = f (x + ∆x, y + ∆y) − f (x, y)
du =
记作
∂u + dz ∂z
dz u
dx u , d y u , dz u称为偏微分 故有下述叠加原理 偏微分. 偏微分 d u = d x u + d y u + dz u
1. 微分定义:
∆z =
+ o(ρ)
ρ = (∆x) + (∆y)
2
2
d z = f x (x, y)dx + f y (x, y)dy
ρ = (∆x) + (∆y)
2
2
d z = f x (x, y)dx + f y (x, y)dy
的全微分.
yz ) d y ze
练习： 练习：设
注意: 注意 x , y , z 具有 x 解: Q f (x,0,0) = 轮换对称性 3 + cos x 1 x ′ = ) ∴ f x (0,0,0) = ( 3 + cos x x = 0 4
1 f y (0,0,0) = f z (0,0,0) = 4 ∴d f (0,0,0) = f y (0,0,0) d x + f y (0,0,0) d y + f z (0,0,0) d z 1 = (d x + d y + d z) 4
(∆x)2 + (∆y)2 ∆x ∆y = 0 2 2 (∆x) + (∆y)
≠ o(ρ ) 因此,函数在点 (0,0) 不可微 .
定理2 定理 (充分条件) 若函数
的偏导数
在 (x, y) 连 , 则函数在该点可微分. 点 续 证：∆z = f (x + ∆x, y + ∆y) − f (x, y)
du =
记作
∂u + dz ∂z
dz u
dx u , d y u , dz u称为偏微分 故有下述叠加原理 偏微分. 偏微分 d u = d x u + d y u + dz u
1. 微分定义:
∆z =
+ o(ρ)
ρ = (∆x) + (∆y)
2
2
d z = f x (x, y)dx + f y (x, y)dy
ρ = (∆x) + (∆y)
2
2
d z = f x (x, y)dx + f y (x, y)dy
8.3全微分
２）函数若在某区域D 内各点处处可微分， 函数若在某区域 内各点处处可微分， 内可微分； 则称这函数在 D 内可微分； ３）如果函数z = f ( x , y )在点( x , y ) 可微分, 则 . 函数在该点连续． 函数在该点连续．
6
４）一元函ห้องสมุดไป่ตู้在某点的导数存在 多元函数的各偏导数存在
微分存在． 微分存在． 全微分存在． 全微分存在．
=3 注意记号 dS ( 3,4 ) = dS x =4 . y
10
例２
的全微分． 求 z = x 2 y + y 2 的全微分． ∂z ∂z = 2 xy , = x 2 + 2 y , ∂x ∂y ∂z ∂z dz = ⋅ dx + ⋅ dy = 2 xydx + ( x 2 + 2 y )dy . ∂x ∂y 的全微分． 求 u = ln( x 2 + y 2 + z 2 ) 的全微分． ∂u 2x 2x ∂u 2y = 2 , = 2 , 2 2 2 2 ∂x x + y + z ∂y x + y + z ∂u 2z , = 2 2 2 ∂z x + y + z ∂u ∂u ∂u 2( xdx + ydy + zdz ) du = ⋅ dx + ⋅ dy + ⋅ dz = . 2 2 2 ∂x ∂y ∂z x + y +z
∂z ∂z , 在点 ( x , y ) ∂x ∂y
∂z ∂z 由此我们看到， 由此我们看到， ∆z ≈ ⋅ ∆x + ⋅ ∆y ∂x ∂y
只是舍弃了高阶无穷小，因此用此近似公式 只是舍弃了高阶无穷小， 计算函数的全增量，具有良好的近似程度． 计算函数的全增量，具有良好的近似程度．
第一轮复习之多元函数微分学
( x0 , y0 )
∂f ( x0 , y0 ) f ( x0 + ∆x, y0 ) − f ( x0 , y0 ) = lim 0 ∆ x → ∂x ∆x
与一元函数连续性的概念相似：
f ( x) = f ( x0 ) xlim →x
0
f ( x) lim f ( x) f ( x0 ) = = xlim →x + x→ x −
(二) 多元函数取得极值的充分条件和必要条件 必要条件：
在点 ( x0 , y0 ) 具有二 阶偏导数
在点 ( x0 , y0 ) 具有偏导数
f x′( x0 , y0 ) = 0 f y′( x0 , y0 ) = 0
f ( x, y ) 在 M 0 ( x0 , y0 ) 取得极值
充分条件：
极限与无穷小的关系
( x , y ) → ( x0 , y0 )
lim
f ( x, y ) = A
f ( x, y )= A + ∂ ( x, y )
其中：
x , y → x0 , y0
lim ∂ ( x, y ) = 0
2、 二元函数与一元函数有相同的极限运算法则与极限性质 求二元函数极限常用的方法：
f ( x, y ) 在 M 0 ( x0 , y0 ) 有极大值，点 M 0 ( x0 , y0 ) 称为 f ( x, y ) 的极值点。
极大值和极小值统称为极值。
驻点：
（x, y） 称为 f ( x, y ) 能够使 f x′( x, y ) = 0 和 f y′( x, y ) = 0 同时成立的点 的驻点。
二. 二元函数的极限 1、 二元函数极限的定义：
设函数 f ( x, y ) 在开区域内或闭区域 D 内有定义， M 0 ( x0 , y0 ) 是 D 的内点， 或者边界点。
全微分的几何意义
全微分的几何意义
全微分的几何意义
全微分在几何学中是一个重要的概念，代表着在某一点处空间函数的值及其一
维梯度，完全体现了函数在改点处的局部变化趋势。
全微分和微积分之间存在一定的联系，可以写出函数的全微分来描述函数的局
部变化，并通过求解全微分的积分来获得函数的总变化。
在几何学中，全微分也表示着一种让一个平面曲面跟一条曲线的投影变换。
比如，投影变换矩阵可以用全微分来表示，把几何图形中的线段映射到另一个空间中，得到线段的映射。
另外，全微分也可以用来表达曲率，将平面曲面表示成一系列点，通过求解曲
面的全微分，就能知道曲面的曲率。
全微分的几何意义是获得一个函数的局部变化趋势，描述曲面的投影变换，求
出曲率，这些均根据函数的微积分而得到。
全微分的定义和计算可以帮助我们更好的理解几何性质的一些重要的现象。
《高数全微分方程》课件
参数方程法
总结词
参数方程法是通过引入参数，将全微分 方程转化为参数微分方程，然后求解参 数的微分，最后得到原全微分方程的解 。
VS
详细描述
参数方程法的步骤包括引入参数、将全微 分方程转化为参数微分方程、求解参数的 微分、将参数的解代回原方程，最后得到 原全微分方程的解。这种方法适用于具有 参数形式的全微分方程，能够简化求解过 程。
变量分离法
总结词
变量分离法是将全微分方程转化为可分离变量的微分方程，然后分别求解每个变量的微分，最后得到 原全微分方程的解。
详细描述
变量分离法的步骤包括将全微分方程转化为可分离变量的微分方程、分别求解每个变量的微分、将各 个变量的解代回原方程，最后得到原全微分方程的解。这种方法适用于具有可分离变量形式的全微分 方程，能够简化求解过程。
总结词
全微分方程描述了曲线的斜率在各个方向上的变化情 况。
详细描述
全微分方程可以表示曲线上任意一点的切线斜率的变 化情况，即该点处曲线在各个方向上的弯曲程度。通 过求解全微分方程，可以了解曲线的弯曲程度，从而 更好地理解曲线的几何特性。
曲线的弯曲程度与全微分方程
总结词
全微分方程描述了曲线的弯曲程度在各个方向上的变 化情况。
二阶全微分方程实例
总结词
二阶全微分方程是描述物理现象和工程问题的重要工具，具有丰富的数学性质和实际应 用价值。
详细描述
二阶全微分方程的一般形式为 d²y/dx² = f(x, y, dy/dx)，其中 f(x, y, z) 是关于 x、y 和 z 的函数。通过求解二阶全微分方程，可以找到满足特定边界条件的解，从而解决实际
高数全微分方程目录来自• 全微分方程简介 • 全微分方程的求解方法 • 全微分方程的实例分析 • 全微分方程的几何意义 • 全微分方程的扩展知识