微分的几何意义

常微分方程几何解释常微分方程（ordinary differential equation）是数学中的一个重要分支，解决了很多实际问题，从而推动了科学和技术的进步。

而常微分方程的几何解释则是其中的一个具有深刻意义的方面，它可以帮助我们更加深刻地理解微分方程的本质，并在几何意义上进行抽象和推广。

一、微分方程的几何意义微分方程是描述自变量和其导数之间的关系的方程，例如：$\frac{dy}{dx} = f(x,y)$其中，$y$ 是变量，$x$ 是自变量，$f(x,y)$ 是一个规定好的函数。

这个式子的意思是，“$y$ 对 $x$ 的导数等于$f(x,y)$”，也就是说，当我们确定了 $f(x,y)$ 这个函数的形式，这个微分方程就规定了 $y$ 在自变量 $x$ 下的变化规律。

那么，这个微分方程到底有什么几何意义呢？我们可以把 $y$ 看作平面上的点，$y$ 对 $x$ 的导数看作该点处的切线斜率，$f(x,y)$ 看作斜率的函数。

这样，微分方程可以被看作描绘了在平面上一点的动态演化轨迹的微分方程。

例如，对于微分方程：$\frac{dy}{dx} = y$我们可以解得 $y = Ce^{x}$ （$C$ 为常数），这个解表明在$x$ 轴正半轴方向上，$y$ 的值不断地成倍增长。

这个动态演化的轨迹可以形象地理解为一条指数曲线。

二、微分方程的向量场由于微分方程描述了一条轨迹，我们可以把它与向量场联系起来，从而更加深入地理解它。

向量场是一个输出为向量的函数，它可以在每个点上给出一个向量，描述了该点的方向和大小。

对于微分方程 $\frac{dy}{dx} =f(x,y)$，我们可以把 $(x,y)$ 看作平面上的一点，$f(x,y)$ 看作向量场在该点的输出。

例如，对于微分方程 $\frac{dy}{dx} = -\frac{x}{\sqrt{x^{2} + y^{2}}}$，我们可以把它看作向量场 $F(x,y) = \left \langle -\frac{x}{\sqrt{x^{2} + y^{2}}},-1 \right \rangle$。

微分和泰勒展开公式是数学分析中两个重要的概念和工具，它们在数学推导和物理问题求解中起着至关重要的作用。

本文将综述微分和泰勒展开公式的关系，旨在深入探讨它们之间的内在通联和应用。

一、微分的基本概念1.微分的定义和性质2.微分在函数求导和近似计算中的应用3.微分的几何意义和物理意义二、泰勒展开公式的基本原理1.泰勒展开公式的定义和表达形式2.泰勒展开公式在函数逼近和级数求和中的应用3.泰勒展开公式的推导和证明方法三、微分和泰勒展开公式的关系1.微分与泰勒展开公式的通联和区别2.微分在泰勒展开公式中的角色和作用3.泰勒展开公式的导出过程中涉及微分的应用四、微分和泰勒展开公式在数学分析中的应用1.微分和泰勒展开公式在函数极值和凹凸性判定中的应用2.微分和泰勒展开公式在函数逼近和近似计算中的应用3.微分和泰勒展开公式在泛函分析和微分方程求解中的应用五、微分和泰勒展开公式在物理问题中的应用1.微分和泰勒展开公式在力学和动力学中的应用2.微分和泰勒展开公式在电磁学和热力学中的应用3.微分和泰勒展开公式在量子力学和相对论中的应用六、结论微分和泰勒展开公式作为数学分析中的重要概念和工具，不仅在理论研究中发挥着重要作用，也在物理问题求解中具有广泛的应用前景。

深入理解微分和泰勒展开公式的关系，对于加深对数学分析和物理学知识的理解和应用具有重要意义。

通过以上关于微分和泰勒展开公式的综述，我们可以更全面深入地了解它们的内在通联和应用，希望本文能对相关领域的研究者和学习者有所启发和帮助。

七、微分的基本概念微分是微积分学中的一个基本概念，它源自导数的概念。

在数学上，微分可以解释为函数的局部线性逼近，可以用来求函数的变化率、切线方程、极值点等等。

微分的定义和性质是我们理解微分和泰勒展开公式的基础。

微分的定义是指当自变量的增量趋于0时，函数增量与自变量增量之比的极限，即：\[ f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x}微分的一些基本性质包括线性性、乘积法则、商法则等，这些性质对于微分求导以及在泰勒展开中的应用都起着重要的作用。

微分和积分的几何意义
微积分是数学中的重要分支，其中微分和积分是微积分的两个主要部分。

它们在解决各种问题中发挥着关键作用。

微分和积分的几何意义是指它们在几何学中的应用。

微分和积分在几何学中有很多应用。

微分被用来描述曲线或曲面的切线或法线方向，它们也被用来计算一条弧线、曲线或曲面的长度、面积、体积以及其他相关的物理量。

积分则被用来计算曲线、曲面或体积的面积或容积。

微分和积分也被用于研究连续性、不连续性和导数在几何上的应用，如单调性、凸性和曲率。

微积分也被广泛用于物理学、工程学和其他领域，如金融学、经济学和计算机科学等。

总之，微分和积分在几何学中有着广泛的应用，是解决各种问题的重要工具。

了解微分和积分的几何意义对深入理解微积分的操作和应用至关重要。

- 1 -。

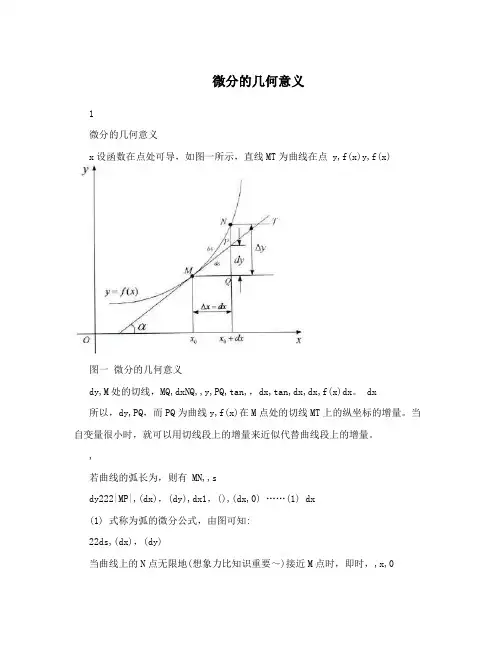
微分的几何意义1微分的几何意义x设函数在点处可导，如图一所示，直线MT为曲线在点 y,f(x)y,f(x)图一微分的几何意义dy,M处的切线，MQ,dxNQ,,y,PQ,tan,，dx,tan,dx,dx,f(x)dx。

dx所以，dy,PQ，而PQ为曲线y,f(x)在M点处的切线MT上的纵坐标的增量。

当自变量很小时，就可以用切线段上的增量来近似代替曲线段上的增量。

,若曲线的弧长为，则有 MN,,sdy222|MP|,(dx)，(dy),dx1，(),(dx,0) ……(1) dx(1) 式称为弧的微分公式，由图可知:22ds,(dx)，(dy)当曲线上的N点无限地(想象力比知识重要～)接近M点时，即时，,x,0,曲线的弧长为转化为直线(切线MP)。

此时，(增量等于微分)。

MN,,s,s,ds 根据导数与微分的关系、导数与积分的关系，由基本初等函数的求导公式和积分公式，可以直接推出其微分和积分公式。

2 函数的导数我们是这样定义的:设函数在点x0处及其近旁有定义，当自变量 y,f(x)x在x0处有增量时，相应地函数y有增量。

,x,y,f(x，,x),f(x),,,y 的极限存在，这个极限称为函数y=f(x)在点x0处的如果lim ,x,0,x导数(或称为变化率)，记为:y, fx，,x,fx()(),,,lim,y, limx,x,x,00x,,x,0 ,x,y如果极限不存在，就说函数y=f(x)在点x0处不可导。

lim ,x,0,x根据导数的定义，求函数 y=f(x) 的导数的三个步骤:,y,f(x，,x),f(x)1.求增量: (1),yf(x，,x),f(x)2.算比值:,……(2) ,x,x,yfx，,x,fx()()3.取极限: ,y,,limlim,x,0,x,0,x,x (3)2y,x例1 求函数的导数。

解: (1)求增量:222,,，,,yfxxfx()(),，,,,,，,()2()xxxxxx,y(2)算比值:,2x，,x,x,y(3)取极限: ,y,lim,lim(2x，,x),2x ,x,0,x,0,x同理可得: nn,1,(x),nx(n为正整数) 。

向量微分的几何意义第一篇嘿，朋友！今天咱们来聊聊向量微分的几何意义，这可有趣啦！想象一下，向量就像是一个有方向的小箭头。

那向量微分呢，就像是在观察这个小箭头怎么一点点变化的。

比如说，在平面上的一个向量，它的微分能告诉我们这个向量的长度和方向是怎么改变的。

这就好像是这个小箭头在跳舞，每一步的舞步变化都被我们看在眼里。

如果这个向量是描述物体的运动，那微分就更厉害啦！它能告诉我们物体运动的速度和加速度的变化。

速度的变化就是速度这个向量的微分呀。

从几何的角度看，向量微分就像是在给我们放一个关于向量变化的小电影，每一帧都能看出细微的差别。

再比如说，曲线的切向量的微分，能让我们知道曲线在那一点弯曲的程度。

就像是在摸一条弯曲的小路，微分能告诉我们路的弯曲是怎么一点点变化的。

是不是觉得向量微分很神奇？它让我们能更清楚地看到数学世界里那些隐藏的变化和规律！好啦，今天就先聊到这儿，下次咱们继续探索向量微分的奇妙世界！第二篇亲，来，咱们一起走进向量微分的几何意义这个神奇的领域！你看哦，向量微分就像是一个神秘的魔法钥匙，能打开几何世界里好多未知的大门。

比如说一个向量代表了空间中的一个位移，那它的微分就是在告诉我们每一瞬间这个位移的变化细节。

这就好像是在仔细观察一只小蜜蜂飞行时的姿态变化。

从图形上看，向量微分能帮助我们描绘出曲线或者曲面的各种特性。

想象一下一条弯弯的曲线，向量微分就能告诉我们在每个点上曲线是怎么“转弯”的，是不是很神奇？还有哦，如果把向量看成是力的表示，那微分就可以告诉我们力的变化情况。

就像是在感受拔河比赛中，双方力量的微妙变化一样。

而且哦，向量微分在物理中也超级重要！比如电磁场中的电场强度和磁场强度，它们的变化用向量微分来描述，就能让我们更好地理解那些看不见摸不着的电磁现象。

呢，向量微分的几何意义就像是给我们戴上了一副特别的眼镜，让我们能看到平常看不到的几何世界里那些细微又奇妙的变化，是不是超级酷？好啦，今天关于这个的分享就到这儿啦，期待下次和你继续畅聊数学的奇妙之处！。