2019年优生堂初一数学寒假衔接班(寒假补课讲义)

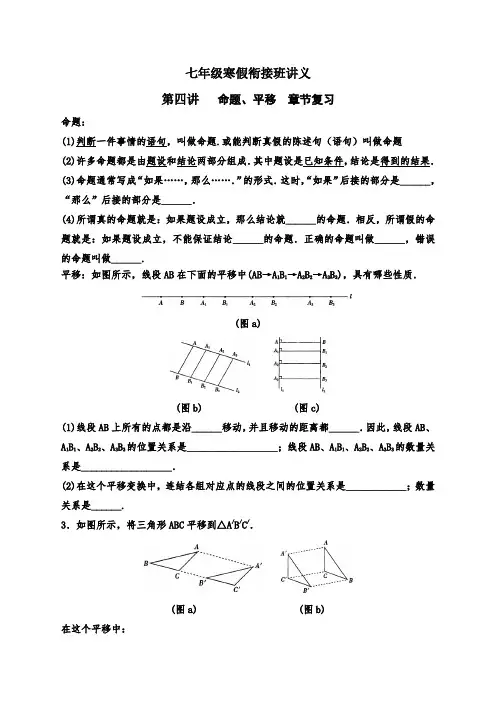
七年级寒假衔接班讲义第四讲命题、平移章节复习命题：(1)判断一件事情的语句，叫做命题.或能判断真假的陈述句（语句）叫做命题(2)许多命题都是由题设和结论两部分组成．其中题设是已知条件，结论是得到的结果．(3)命题通常写成“如果……，那么……．”的形式．这时，“如果”后接的部分是______，“那么”后接的部分是______．(4)所谓真的命题就是：如果题设成立，那么结论就______的命题．相反，所谓假的命题就是：如果题设成立，不能保证结论______的命题．正确的命题叫做______，错误的命题叫做______.平移：如图所示，线段AB在下面的平移中(AB→A1B1→A2B2→A3B3)，具有哪些性质．(图a)(图b) (图c)(1)线段AB上所有的点都是沿______移动，并且移动的距离都______．因此，线段AB、A1B1、A2B2、A3B3的位置关系是__________________；线段AB、A1B1、A2B2、A3B3的数量关系是__________________．(2)在这个平移变换中，连结各组对应点的线段之间的位置关系是____________；数量关系是______.3．如图所示，将三角形ABC平移到△A/B/C/．(图a) (图b)在这个平移中：(1)△ABC的整体沿____移动，得到△A/B/C/．△A/B/C/与△ABC的____和______完全相同．(2)连结各组对应点的线段即AA/、BB/、CC/之间的数量关系是____；位置关系是______. 一个图形沿着某个方向．．移动一定的距离．．,图形的这种移动,叫做平移变换,简称平移.例1.指出下列命题的题设和结论：(1)垂直于同一条直线的两条直线平行．题设是_________________________；结论是_________________________. (2)同位角相等，两直线平行．题设是________________________；结论是_________________.(3)两直线平行，同位角相等．题设是_____________________；结论是________________________.(4)对顶角相等．题设是_____________________；结论是_____________________.例2.将下列命题改写成“如果……那么……”的形式：(1)900的角是直角．__________________________(2)末位数字是零的整数能被5整除．_______________________________(3)等角的余角相等．______________________________(4)同旁内角互补，两直线平行．_____________________________例3.已知：如图，CB⊥AB，CE平分∠BCD，DE平分∠CDA,∠1+∠2=900，求证：DA⊥AB.课堂练习：1.下列语句哪些是命题，哪些不是命题?(1)两条直线相交，只有一个交点．( )．(2)不是有理数．( )．(3)直线a与b能相交吗?( )． (4)连结AB．( )．(5)作AB⊥CD于E点．( )． (6)三条直线相交，有三个交点．( )．2.判断下列各命题中，哪些命题是真命题?哪些是假命题?(对于真命题画“√”，对于假命题画“×”)(1)0是自然数．( )．(2)如果两个角不相等，那么这两个角不是对顶角．( )．(3)相等的角是对顶角．( )．(4)如果AC=BC，那么C点是AB的中点．( )．(5)若a∥b，b∥c，则a∥c．( )．(6)如果C是线段AB的中点，那么AB＝2BC．( )．(7)若x2=4，则x=2．( )． (8)若xy=0，则x=0．( )．(9)同一平面内既不重合也不平行的两条直线一定相交．( )．(10)邻补角的平分线互相垂直．( )．(11)同位角相等．( )． (12)大于直角的角是钝角．( )．3.按要求画出相应图形．(1)已知:如图,AB∥DC,AD∥BC,DE⊥AB于E点,将三角形DAE平移,得到三角形CBF．(2)已知:如图,AB∥DC,将线段DB向右平移，得到线段CE．(3)已知:平行四边形ABCD及A/点,将平行四边形ABCD平移,使A点移到A/点,得平行四边形A/B/C/D/．(4)已知:五边形ABCDE，及点A/点,将五边形ABCDE平移,使A点移到A/点,得到五边形A/B/C/D/E/．11.如图，BD平分∠ABC，DF∥AB，DE∥BC，求∠1与∠2的大小关系．12.如图,已知∠ABC+∠ACB=1100，BO、CO分别是∠ABC和∠ACB的平分线，EF过点O 与BC平行，求∠BOC的度数。

七年级寒假衔接班讲义第五讲平方根1. 乘方：“a n” .乘方的结果叫做幕，a叫做底数，n叫做指数，读作a的n次方或a 的n 次幕.2. 平方：“ a2”，读作a的平方或a的二次方.3. 平方的性质：任何数的平方都是非负数；算术平方根概念：一般地，如果一个正数的平方等于a,那么这个数叫做a的算术平方根，也就是说，如果x2=a，（x>0）那么x叫做a的算术平方根.则x ..a算术平方根性质:a(a 0)(由定义得出)a(a 0)⑴当a 0时・,a 0 （由定义得出）即非负数的算术平方根是非负数（2）个数性质：正数和0的算术平方根据都只有一个（3）还原性质：当a 0时，（.、a）2 a,即非负数算术平方根的平方等于该非负数完全平方数：能够完全开方开的尽的数。

如1,4,9,16 ，...平方根概念：一般地，如果一个数的平方等于a，那么这个数叫做a的平方根或二次方根，也就是说，如果x2=a，那么x叫做a的平方根.则x ,a开平方：求一个数a的平方根的运算叫做开平方.即求,a的运算叫开平方.表示方法：一个正数a的平方根表示为 a ;若x2=a （a >0）则x= a。

平方根的性质：（1）个数性质：正数有两个平方根，它们互为相反数,0只有一个平方根就是0本身.负数没有平方根⑵还原性质：（由定义得出）当a 0时（.a）2=a 即:非负数的平方根的平方等于该数（三）,a, .a,a的含义：> a :当a 0时，表示a的算术平方根-、.a :当a 0时，表示a 的算术平方根的相反数、、a :当a 0时，表示a 的平方根平方根的求法： 逆运算法，查表法，计算器，式子计算查表法的理论根据： 如果正数的小数点向右或向左移动 2位，那么它的算术平方根 的小数点就相应地向右、向左移动一位• 查表外数小数点移动法则：(1) 被开方数的小数点要两位两位地移动，移动到使被查数成为有一位或两位整数的 数 (2) 被开方数的小数点每移动两位，查得的算术平方根的小数点要向相反方向移动一 位。

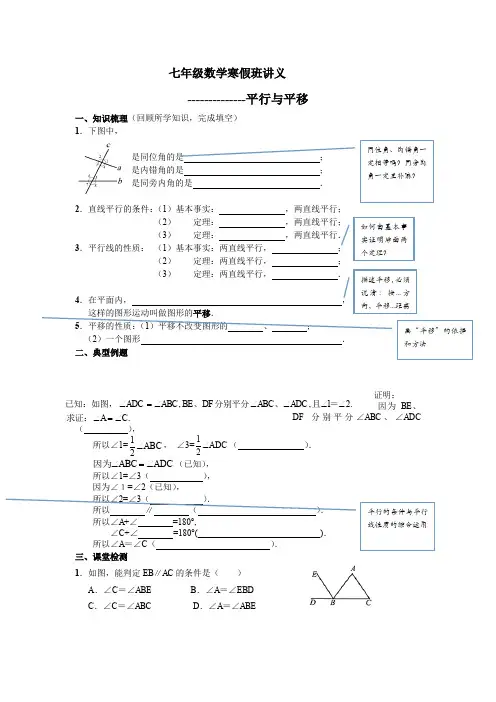
..21,,C A ADC ABC DF BE ABC ADC ∠=∠∠∠∠∠∠=∠求证：＝且、分别平分、已知：如图， 七年级数学寒假班讲义--------------平行与平移一、知识梳理（回顾所学知识，完成填空） 1．下图中，是同位角的是； 是内错角的是 ； 是同旁内角的是 ．2．直线平行的条件：（1）基本事实： ，两直线平行； （2） 定理： ，两直线平行； （3） 定理： ，两直线平行． 3．平行线的性质： （1）基本事实：两直线平行， ； （2） 定理：两直线平行， ； （3） 定理：两直线平行， ．4．在平面内， ， （2）一个图形 ． 二、典型例题证明：因为BE 、DF 分别平分∠ABC 、∠ADC （ ），所以∠1=，∠3=（ ）．（已知）， 所以∠1=∠3（ ），因为∠１=∠2（已知），所以 ∥ （ ）所以∠A +∠ =180°, ∠C +∠ =180°( )． 所以∠A ＝∠C （ ）． 三、课堂检测 1．如图，能判定EB ∥AC 的条件是（ ） A ．∠C ＝∠ABE B ．∠A ＝∠EBD C ．∠C ＝∠ABC D ．∠A ＝∠ABEABC ∠21ADC ∠21ADC ABC ∠=∠因为如何由基本事实证明后面两个定理？ 同位角、内错角一定相等吗？同旁内角一定互补嘛？描述平移，必须说清：按...方向，平移...距离画“平移”的依据和方法平行的条件与平行线性质的综合运用2．如图，直线a ∥b ，∠1＝70°，那么∠2= °．3．如图，将一个长方形纸条折成如图的形状，若已知∠1＝130°，则∠2＝ °．（第2题） （第3题） （第4题） （第5题） 4．如图，把边长为3cm 的正方形ABCD 先向右平移1cm ，再向上平移1cm ，得到正方形 EFGH ，则阴影部分的面积为 cm ²．5．把图中的一个三角形先横向平移x 格，再纵向平移y 格，可以与另一个三角形拼合成一 些不同形状的四边形．那么移动的总格数(x +y )的值最小为 ． 6．如图，点D 在AB 上，直线DG 交AF 于点E ．请从①DG ∥AC ，②AF 平分∠BAC ，③∠ADE ＝∠DEA ． 中任选两个作为条件，余下一个作为 结论，构造一个真命题，并说明理由． 已知： ， 求证： ．（填写序号） 证明：7．如图，在△ABC 中，CD ⊥AB ，垂足为D ，点E 在BC 上，EF ⊥AB ，垂足为F ． （1）CD 与EF 平行吗？为什么？（2）如果∠1=∠2，且∠3=115°，求∠ACB 的度数．四：拓展归类1.如图、直线a 、b 被c 所截，所标出的角中有哪些角是同位角？同位角一定相等吗？8765cab 4321b ac 78126543 a bc 56 4 81 23 7 ab122.三类角的位置特征、基本图形、图形结构特征如下表：3.（1）同位角和同旁内角在位置上有什么相同点和不同点？内错角和同旁内角在位置上有什么相同点和不同点？ （2）这三类角的共同特征是什么？总结：五、范例点睛例1、如图（1），∠1和∠2是直线_______、_______被直线_______所截得的_______角，∠2和∠3是直线_______、_______被直线_______所截得的_______角；如图（2），∠1和∠2是直线_______、_______被直线_______所截得的_______角，∠4和∠3是直线_______、_______被直线_______所截得的_______角。

第1讲 同底数幂的乘法一、新知探索1．同底数幂的乘法法则：同底数幂相乘，底数不变，指数相加。

即nm nmaa a +=⋅ (m ，n 都是正整数)．注意：① 三个或三个以上同底数幂相乘时，也具有这一性质．如：p n m p n m a a a a ++=⋅⋅ (m ，n ，p 都是正整数)． ② 此性质可以逆用：n m nm a a a⋅=+说明：在幂的运算中，经常会用到以下的一些变形：（－a ）n＝⎪⎩⎪⎨⎧-);(),(为奇数为偶数n a n a n n （b －a ）n＝⎪⎩⎪⎨⎧---).()(),()(为奇数为偶数n b a n b a n n二、典例剖析1、顺用公式：例1、计算：（1）35aa a （2）35xx- (3) 231mm bb +⋅（4）m n p a a a ⋅⋅ （5）()()7633-⨯- （6）()()57a a a ---变形练习：（1）234aa a a （2）()()48x x x ---2、常用等式： ()()b a a b -=-- ()()22b a a b -=-()()33b a a b -=--()()44b a a b -=-()()2121n n b a a b ++-=--()()22nnb a a b -=-例2、（1）()()()38b a b a b a --- （2）()()()21221222n n n x y y x x y +----（3）()()()48x y y x y x --- （4）()()()37x y y x y x ---3、逆用公式：例3、已知：64,65mn== ，求：6m n+的值。

变形练习：（1）已知：7,6mn a a == ，求：m n a +的值。

（2）已知：2129,5m m aa ++==，求：33m a+的值。

4、利用指数相等解题：例4、（1） 已知：2111m a a +=，求：m 的值；（2） 已知1239m n x xx +-=，求2m n +的值。

七年级寒假衔接班讲义第三讲平行线的性质平行线的性质：（1)两条平行线被第三条直线所截，同位角相等。

简记:两直线平行，同位角相等。

（2）两条平行线被第三条直线所截，内错角相等。

简记：两直线平行,内错角相等。

（3)两条平行线被第三条直线所截，同旁内角互补。

简记：两直线平行，同旁内角互补。

例1.已知:如图,请分别根据已知条件进行推理，得出结论，并在括号内注明理由．（1）如果AB ∥EF ，那么∠2=______，理由是___________________________.（2)如果AB ∥DC ，那么∠3=______，理由是____________________________________。

(3）如果AF ∥BE ，那么∠1+∠2=______，理由是_______________________________。

(4)如果AF ∥BE ，∠4=120°,那么∠5=______，理由是________________________。

例 2.已知：如图，DE ∥AB ．请根据已知条件进行推理，分别得出结论，并在括号内注明理由．（1）∵DE ∥AB ，( )∴∠2=______。

（ , )（2)∵DE ∥AB ，（ ）∴∠3=______.（ ， )（3）∵DE ∥AB （ ）,∴∠1＋______=180°．( ， )例3.如图，若AB ∥DE ，∠B=1350，∠D=1450,你能求出∠C 的度数吗？在AB ∥DE 的条件下，你能得出∠B 、∠C 、∠D 之间的数量关系吗？并说明理由．例4.如图所示，AB//CD，∠A=1350,∠E=800,求∠CDE的度数。

例5。

如图，已知：∠BAP与∠APD互补,∠1=∠2，说明:∠E=∠F.例6。

如图，已知AB∥CD，P为HD上任意一点,过P点的直线交HF于O点，试问：∠HOP、∠AGF、∠HPO有怎样的关系？用式子表示并证明。