下载文档原格式
一、实验目的
1. 掌握组合逻辑电路的功能测试。
2. 验证半加器和全加器的逻辑功能。
3. 学会二进制数的运算规律。
二、实验原理及其实验元件
实验原理：参照指导书对应内容结合自己理解写
实验箱、芯片（74LS00、74LS10、74LS54、74LS86）、导线。
三、实验内容及其步骤
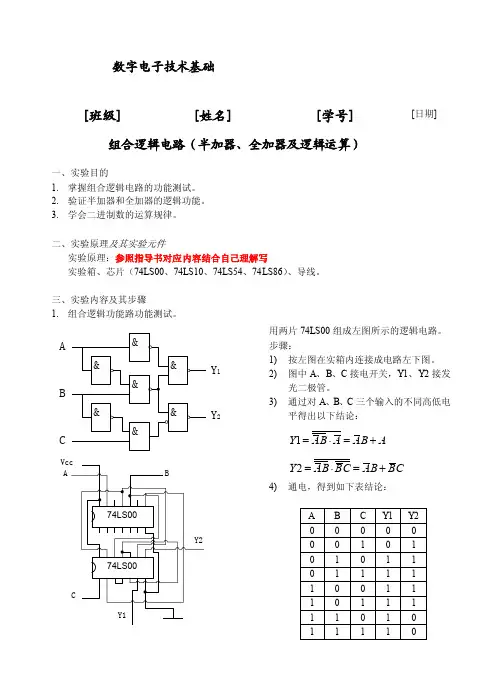
数字电子技术基础
组合逻辑电路（半加器、全加器及逻辑运算）
[班级] [姓名] [学号]
[日期]
2.测试用异或门（74LS86）和与非门组成的半加器的逻辑功能。
用一片（74LS86）和（74LS00）组成半加器。
3.测试用异或门、与或门和非门组成的全加
器的逻辑功能。
S
CO
设计性实验
设计一个“三个一至电路”。
电路有三个输入端，一个输出端。
当三个输入端变量A、B、C状态一致时，输出F为“1”；当三个变量状态不一致时，输出F为“0”。
（要求：用与非门组成电路。
）
步骤：
1)列真值表：
2)写出逻辑表达式:
()()
ABC
C
B
A
F⋅
=
3)画逻辑电路图：
A
B
C
F
4)验证：
所得实验结论与理论值相等，说明实验成功。
5)按下图连接实验电路。
A
B。
与非门和异或门构成的半加器、全加器的工作原理一、半加器的工作原理半加器是数字电路中常见的逻辑电路，用于将两个输入位进行加法运算，得到一个和位和一个进位位。
半加器是由两个逻辑门组成的，分别是异或门和与门。
异或门用于求和位，而与门用于求进位位。
1. 异或门的作用异或门也叫做互斥或门，它的主要作用是将两个输入按位进行异或运算，得到一个输出。
异或门的逻辑符号为^，其真值表如下：| A | B | A^B ||---|---|-----|| 0 | 0 | 0 || 0 | 1 | 1 || 1 | 0 | 1 || 1 | 1 | 0 |由真值表可以看出，异或门的输出为1的条件是两个输入不同，即为异或运算的性质。
2. 与门的作用与门的功能是将两个输入按位进行与运算，得到一个输出。
与门的逻辑符号为&，其真值表如下：| A | B | A&B ||---|---|-----|| 0 | 0 | 0 || 0 | 1 | 0 || 1 | 0 | 0 || 1 | 1 | 1 |从与门的真值表可以看出，只有当两个输入都为1时，与门的输出才为1。
3. 半加器的组成半加器由一个异或门和一个与门组成，其电路图如下：```A-----------\\B-----------[XOR]----S/C-----------/O```A和B分别是两个输入位，[XOR]代表异或门，S是和位的输出，C是进位位的输出。
半加器的工作原理是：将输入A和B分别作为异或门的两个输入，得到和位S的输出；然后将输入A和B分别作为与门的两个输入，得到进位位C的输出。
二、全加器的工作原理全加器是在半加器的基础上进一步发展而来的，用于将三个输入位进行加法运算，得到一个和位和一个进位位。
全加器由两个半加器和一个或门组成，在实际的数字电路中，通常使用两个半加器和一个或门联接在一起构成全加器。
1. 两个半加器的作用两个半加器用于分别处理两个低位和两个高位的加法运算，其工作原理和半加器相似，只是需要考虑进位的传递。
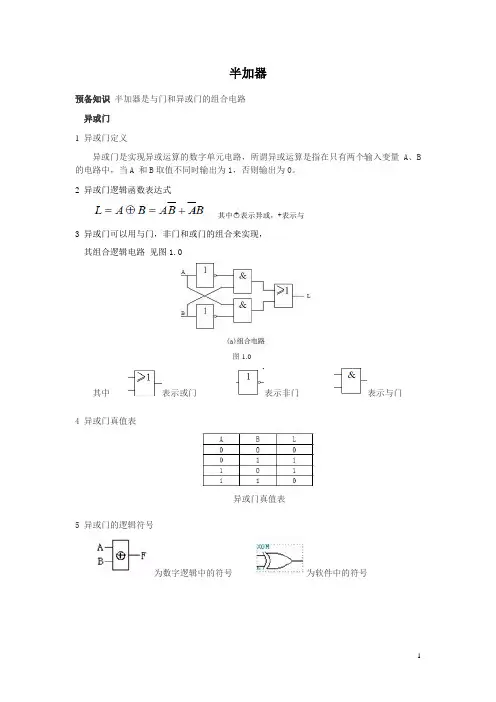
半加器预备知识半加器是与门和异或门的组合电路异或门1 异或门定义异或门是实现异或运算的数字单元电路，所谓异或运算是指在只有两个输入变量A、B 的电路中，当A 和B取值不同时输出为1，否则输出为0。
2 异或门逻辑函数表达式其中○+表示异或，+表示与3 异或门可以用与门，非门和或门的组合来实现，其组合逻辑电路见图1.0图1.0其中表示或门表示非门表示与门4 异或门真值表异或门真值表5 异或门的逻辑符号为数字逻辑中的符号为软件中的符号二半加器知识介绍1．半加器定义半加器能实现两个一位二进制数的算术加法及向高位进位，而不考虑低位进位的逻辑电路。
它有两个输入端，两个输出端。
半加器用异或门及与门来实现。
2. 真值表两个一位二进制半加器的运算类似于十进制运算，区别是二进制半加器是逢2向高位进一，十进制是逢十向高位进一。
两个一位二进制半加器的运算法则为 0+0=0；1+0=1；0+1=1；1+1=0,同时向高位进1.根据两个一位二进制半加器的运算法则，我们得出其真值表，如下：3. 输出逻辑表达式通过观测真值表很容易看出：A,B相异时，输出和数C为1；A,B相同时，输出和数C 为0；A,B都为1时，输出进位数D为1；否则输出进位数D为0.据此我们得出如下:C=A○+B,D=A•B 注：○+表示异或，•表示与4.半加器的逻辑电路图图2.0其中为异或符号为与符号5功能仿真图功能仿真又叫逻辑仿真，是指在不考虑器件延时和布线延时的理想情况下对源代码进行逻辑功能的验证。
图3.0○1加数A为1，被加数B为0时，输出和数C为1，进位数D为0；○2加数A为1，被加数B为1时，输出和数C为0，进位数D为1；○3加数A为0，被加数1为0时，输出和数C为1，进位数D为0；○4加数A为0，被加数B为0时，输出和数C为0，进位数D为0；6 时序仿真图时序仿真是在将设计适配到芯片后的仿真验证方式。
时序仿真在严格的仿真时间模型下，模拟芯片的实际运作。
组合逻辑电路实验（半加器全加器及逻辑运算）一、实验目的1、掌握组合逻辑电路的功能测试。
2、验证半加器和全加器的逻辑功能。
3、学会二进制数的运算规律。
二、实验原理数字电路分为组合逻辑电路和时序逻辑电路两类。
任意时刻电路的输出信号仅取决于该时刻的输入信号，而与信号输入前电路所处的状态无关，这种电路叫做组合逻辑电路。
分析一个组合电路，一般从输出开始，逐级写出逻辑表达式，然后利用公式或卡诺图等方法进行化简，得到仅含有输入信号的最简输出逻辑函数表达式，由此得到该电路的逻辑功能。
两个一位二进制数相加，叫做半加，实现半加操作的电路称为半加器。
两个一位二进制数相加的真值表见表5-1，表中Si表示半加和，Ci表示向高位的进位，Ai、Bi表示两个加数。
表5-1 半加器真值表从二进制数加法的角度看，表中只考虑了两个加数本身，没有考虑低位来的进位，这也就是半加一词的由来。
由表5-1可直接写出半加器的逻辑表达式： 、Ci=AiBi由逻辑表达式可知，半加器的半加和Si是Ai、Bi的异或，而进Si=AiBi AiBi位Ci 是Ai 、Bi 相与，故半加器可用一个集成异或门和一个与门组成。
两个同位的加数和来自低位的进位三者相加，这种加法运算就是全加，实现全加运算的电路叫做全加器。
如果用Ai 、Bi 分别表示A 、B 两个多位二进制数的第i 位，1i C -表示低位（第i-1位）来的进位，则根据全加运算的规则可列出真值表如表5-2。
表5-2 全加器的真值表利用卡诺图可求出Si 、Ci 的简化函数表达式：i i i i-1i i i i i i S =A B C C =(A B )C +A B ⊕⊕⊕可见，全加器可用两个异或门和一个与或门组成。
如果将数据表达式进行一些变换，半加器还可以用异或门、与非门等元器件组成多种形式的电路（见图5-2，图5-3）。
三、实验仪器及材料 器件：74LS00 二输入端四与非门 3片 74LA86 二输入端四异或门 1片 74LS54 四组输入与或非门 1片四、预习要求1、预习组合逻辑电路的分析方法。
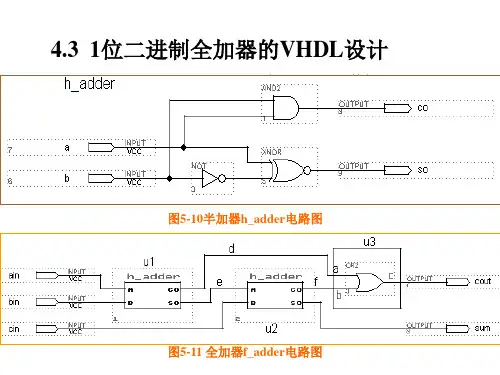
组合逻辑电路设计之全加器半加器全加器和半加器是组合逻辑电路中常用的两种基本电路。
全加器和半加器可以用于实现二进制数的加法运算。
在本文中，将详细介绍全加器和半加器的设计原理和电路结构。
一、半加器半加器是一个用于实现两个一位二进制数相加求和的电路。
半加器的输入包括两个二进制数A和B，输出包括二进制求和信号S和进位信号C。
```A----，--?--SB----，，--CGND```半加器的输出S等于输入A和B的异或（XOR）结果，输出C等于输入A和B的与（AND）结果。
半加器的真值表如下所示：A，B，S，C---，---，---，---0，0，0，00，1，1，01，0，1，01，1，0，1二、全加器全加器是一个用于实现三个一位二进制数相加求和的电路。
全加器的输入包括两个二进制数A和B，以及一个进位信号Cin（来自上一位的进位或者是初始进位信号），输出包括二进制求和信号S和进位信号Cout （输出给下一位的进位信号）。
```A----，--?---SB ----，，--CoutCin --，--?-------CGND```全加器的输出S等于输入A、B和Cin的异或（XOR）结果，输出Cout等于输入A、B和Cin的任意两个的与（AND）结果和输入A、B和Cin的三个的或（OR）结果的与（AND）结果。
全加器的真值表如下所示：A ，B ， Cin ， S ， Cout---，---，-----，---，------0，0，0，0，00，0，1，1，00，1，0，1，00，1，1，0，11，0，0，1，01，0，1，0，11，1，0，0，11，1，1，1，1三、全加器的电路设计可以通过组合半加器的方式来设计一个全加器。
在全加器中，首先使用两个半加器实现输入A和B的求和结果（S1）和对应的进位（C1）；然后再使用一个半加器将输入A和B之间的进位信号（Cin）与求和结果（S1）相加，得到最终的求和结果（S）和进位信号（Cout）。
半加器预备知识半加器是与门和异或门的组合电路异或门1 异或门定义异或门是实现异或运算的数字单元电路，所谓异或运算是指在只有两个输入变量A、B 的电路中，当A 和B取值不同时输出为1，否则输出为0。
2 异或门逻辑函数表达式其中○+表示异或，+表示与3 异或门可以用与门，非门和或门的组合来实现，其组合逻辑电路见图1.0图1.0其中表示或门表示非门表示与门4 异或门真值表异或门真值表5 异或门的逻辑符号为数字逻辑中的符号为软件中的符号二半加器知识介绍1．半加器定义半加器能实现两个一位二进制数的算术加法及向高位进位，而不考虑低位进位的逻辑电路。
它有两个输入端，两个输出端。
半加器用异或门及与门来实现。
2. 真值表两个一位二进制半加器的运算类似于十进制运算，区别是二进制半加器是逢2向高位进一，十进制是逢十向高位进一。
两个一位二进制半加器的运算法则为 0+0=0；1+0=1；0+1=1；1+1=0,同时向高位进1.根据两个一位二进制半加器的运算法则，我们得出其真值表，如下：3. 输出逻辑表达式通过观测真值表很容易看出：A,B相异时，输出和数C为1；A,B相同时，输出和数C 为0；A,B都为1时，输出进位数D为1；否则输出进位数D为0.据此我们得出如下:C=A○+B,D=A•B 注：○+表示异或，•表示与4.半加器的逻辑电路图图2.0其中为异或符号为与符号5功能仿真图功能仿真又叫逻辑仿真，是指在不考虑器件延时和布线延时的理想情况下对源代码进行逻辑功能的验证。
图3.0○1加数A为1，被加数B为0时，输出和数C为1，进位数D为0；○2加数A为1，被加数B为1时，输出和数C为0，进位数D为1；○3加数A为0，被加数1为0时，输出和数C为1，进位数D为0；○4加数A为0，被加数B为0时，输出和数C为0，进位数D为0；6 时序仿真图时序仿真是在将设计适配到芯片后的仿真验证方式。
时序仿真在严格的仿真时间模型下，模拟芯片的实际运作。
