3.4 简单的旋转作图

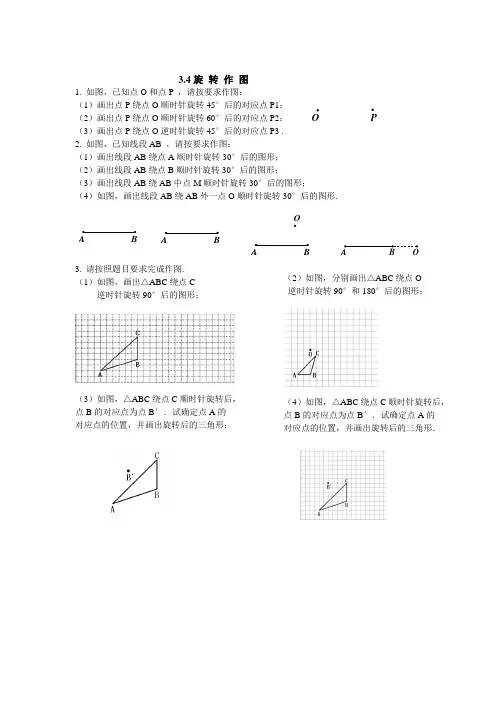
3.4旋 转 作 图1. 如图，已知点O 和点P ，请按要求作图：（1）画出点P 绕点O 顺时针旋转45°后的对应点P1；（2）画出点P 绕点O 顺时针旋转60°后的对应点P2；（3）画出点P 绕点O 逆时针旋转45°后的对应点P3 . 2. 如图，已知线段AB ，请按要求作图：（1）画出线段AB 绕点A 顺时针旋转30°后的图形； （2）画出线段AB 绕点B 顺时针旋转30°后的图形；（3）画出线段AB 绕AB 中点M 顺时针旋转30°后的图形；（4）如图，画出线段AB 绕AB 外一点O 顺时针旋转30°后的图形.3. 请按照题目要求完成作图.（1）如图，画出△ABC 绕点C 逆时针旋转90°后的图形；（3）如图，△ABC 绕点C 顺时针旋转后， 点B 的对应点为点B ′．试确定点A 的 对应点的位置，并画出旋转后的三角形；O A B O B A O（4）如图，△ABC 绕点C 顺时针旋转后， 点B 的对应点为点B ′．试确定点A 的 对应点的位置，并画出旋转后的三角形．（2）如图，分别画出△ABC 绕点O 逆时针旋转90°和180°后的图形；4. （1）如图，已知点P 经过旋转后得到 点 P ′，请找出这个旋转的中心；（3）如图，已知△ABC 经过旋转后得到 △ A ′B ′C ′，点A 、B 、C 的对应点 分别为A ′、B ′、C ′，请找出这个旋 转的中心.6. 将等边△ABC 绕着点A 按某个方向 旋转40°后得到△ADE(点B 与点D 是 对应点)，则∠BAE 为_____________度.P （2）如图，已知线段AB 经过旋转后 得到线段 A ′B ′，点B 的对应点为 点B ′ ，请找出这个旋转的中心；B'AC'A 5. 如图，E 是正方形ABCD 中CD 边上 任意一点，以点A 为中心，把△ADE 顺时针旋转90°，画出旋转后的图形.7. 将下图中大写字母N 绕它右下侧的顶点 按顺时针方向旋转90˚，作出旋转后的图案.。

3.4 简单的旋转作图一、名师解惑1.作简单平面图形旋转后的图形时要考虑的问题.释疑:简单的旋转作图，可先在方格纸上画图，体会旋转的关键是确定旋转中心和旋转角，在自己动手画图的的过程中，自己归纳总结出旋转的关键.作简单平面图形旋转后的图形，要明确旋转中心在哪里，旋转的角度是多少，是顺时针旋转还是逆时针旋转等.另外，尺规作法的要求，仅限于作三角形等基本图形.2.注重旋转作图的常见的考查形式，把握作图的基本原则.释疑:旋转作图的考查形式有三种：一是已知原图、旋转中心和一对对应点，求作旋转后的图形；二是已知原图、旋转中心和一对对应线段，求作旋转后的图形；三是已知原图、旋转中心和旋转角，求作旋转后的图形，这三种考查形式，都是根据定义和性质进行作图.特别地，对于给出原图和一对对应边的作图问题，除可按一般的方法作图外，如果求作的是三角形，还可以用三角形全等的方法作出旋转图形旋转作图的方法是：（1）先找出图形中的关键点；（2）分别作出这几个关键点绕旋转中心旋转后的位置；（3）按原来位置依次连接各点即得要求下旋转后的图形.二、讲练互动【例1】如图，在△ABC中，∠C=90°，以B为中心，按顺时针方向把△ABC旋转90°，请作出旋转后的三角形.AB C A'C''()B【解析】显然，旋转后点B的对应点B′就是点B，另外只需分别作出点A、C绕B旋转90°后的对应点即可.【答案】(1)过点B作AB的垂线并在这条垂线上截取BA′=BA，即得点A的对应点A′.(2)过点B 作BC 的垂线，并在这条垂线上截取BC ′=BC ，即得点C 的对应点C ′.(3)连结A ′C ′.△A ′B ′C ′就是所求作的三角形.【绿色通道】明确旋转中心是点B 和旋转角度是90°是作图的关键，还要明确是顺时针旋转还是逆时针旋转，能够按要求先作出点的旋转，问题就可以解决.【变式训练】1.如图，△ABC 绕C 点旋转后，顶点A 的对应点为点D.试确定顶点B 对应点的位置，以及旋转后的三角形.A B C D【解析】要重视对课本中例题的“分析”的处理，它是对本题解法的点睛之笔.注意“作图”与“画图”的区别：“作图”的工具仅限于直尺、圆规，而“画图”的的工具还可以用刻度尺及量角器.答案:因为△ABC 绕C 点旋转后，顶点A 的对应点为点D ，可见旋转中心为点C ，旋转方向为顺时针，旋转角为∠ACD,所以点B 的对应点为将点B 绕点C 沿顺时针方向转等于∠ACD 的角度即可，则旋转后的图形易得.2.下图中的两个正方形的边长相等，请你指出可以通过绕点O 旋转而相互得到的全等三角形，并说明旋转的角度．【解析】旋转不改变图形的形状和大小，对应角相等可以判别图形的全等.答案:△OAE和△OBF，△OEB和△OFC，△OAB和△OBC，旋转的角度为90°.【例2】如图，四边形ABCD绕点O旋转后，顶点A的对应点为E，试确定B、C、D对应的点的位置，以及旋转后的四边形.BCADEO【解析】A点与E点是对应点，连结AO、EO，则∠AOE为旋转角，O为旋转中心，旋转方向为顺时针.【答案】(1)如图，连结OA、OB、OC、OD、OE.(2)分别以OB、OC、OD为一边作∠BOF、∠COG、∠DOH，使∠BOF=∠COG=∠DOH=∠AOE.(3)分别在射线OF、OG、OH上，截取OF=OB，OG=OC,OH=OD.(4)连结EF、FG、GH、HE.四边形EFGH就是四边形ABCD绕O点旋转后的图形.【绿色通道】通过亲自动手作简单的旋转作图，进一步体验旋转的基本性质.掌握有关画图的操作技能，明确旋转中心、方向和角度是作图的关键，能够按要求作出简单平面图形旋转后的图形并会探索图形之间的旋转关系.【变式训练】1.如图，正方形ABCD绕O点旋转后，顶点A的对应点为A1，试确定B、C、D对应点的位置，以及旋转后的正方形.AA B C D 1O【解析】假设顶点B 、C 、D 的对应点分别为点B 1、C 1、D 1,则∠BOB 1、∠COC 1、∠DOD 1都是旋转角且OB=OB 1,OC=OC 1, OD=OD 1,则B 、C 、D 三点的对应点就找到了，旋转后的正方形就得到了.答案:（1）连接OA 、OA 1、OB 、OC 、OD ；（2）如图，分别以OB 、OC 、OD 为一边作∠BOB 1、∠COC 1、∠DOD 1，使得∠BOB 1=∠COC 1=∠DOD 1=∠AOA 1；1(3)分别在射线OB 1、OC 1、OD 1上截取OB 1=OB 、OC 1=OC 、OD 1=OD ；(4)连接B 1C 1、C 1D 1、D 1A 1、A 1B 1.正方形A 1B 1C 1D 1就是正方形ABCD 绕O 点旋转后的图形.2.下图是一块四边形状薄钢板，∠A=60°,∠C=120°,AB=AD.'（1）能否先沿一条对角线将钢板割成两块，再焊接成一块与原钢板面积相同的三角形状钢板？若能，请说明切割、焊接的方法，用虚线画出示意图，并说明焊接的钢板为什么是三角形状；若不能，请说明理由.(2) 焊接后的△ACC ′是什么形状的三角形？【解析】本题思考的出发点是利用AB=AD ，进行全等旋转变换，看到∠A=60°,∠C=120°，可以完成焊接。

（5）=-2)7( （6）=-2)7(【自主学习】（阅读书本82---83页）【知识点一】：你能作出 “将方格中的小旗子绕 O 点按顺时针方向旋转90˚”后的图案吗？例１ 如图 3—17，△ABC 绕 C 点旋转后，顶点 A 的对应点为点 D 。

试确定 顶点 B 的 对应位置， 以及旋转后的三角形。

作旋转后图形的步骤： 1)、连结_______.2）、以CB 为一边作________________________________________3）、在射线CB 上____________________________4）、连接_________________C归纳得到旋转后图形的作图步骤:1)找到旋转中心 ； 2)找出关键点；3)作出这些点旋转后的对应点；4)将所作的对应点按原来的方式连接。

【练习一】：1.P83 随堂练习1.2.平面图形的旋转一般情况只改变图形的（ ）A.位置B.大小C.形状D.性质3.在图中，将大写字母H 绕它右上侧的顶点按逆时针方向旋转90°，请作出旋转后的图案.4.如图，画出线段A B 绕点O 顺时针旋转90°后得到的图形5.如图,画出∆ABC 绕点O 顺时针旋转180°后得到的图形6.将一个等腰直角三角形ABC （如图∠A 是直角）绕着它的一个顶点B 逆时针方向旋转，分别作出旋转下列角度后的图形.(1)45° (2)180°深化培优:(数学理解P84—3)1) 2)批阅: 中心组长:_______ 科任:_______ 日期:_______OAB。

课题3.4 简单的旋转作图课型新授课课标与教材课标要求：探索图形之间的变换关系，能够按照要求作出简单平面图形旋转后的图形。

图形的旋转是继平移、轴对称之后的又一种图形基本变换，是义务教育阶段数学课程标准中图形变换的一个重要组成部分。

旋转是培养学生思维能力、树立运动变化观点的良好素材。

同时“图形的旋转”也为本章后续学习对称图形、中心对称图形做好准备，为今后学习“圆”的知识内容做好铺垫。

重点：利用基本作图求作简单平面图形旋转后的图形。

难点：正确运用作图的步骤，正确运用作图语言。

学情分析学生已对轴对称、平移这两种简单的全等变换有了很好的认识，并对旋转有了初步的了解。

由于旋转与轴对称、平移都是全等变换，在特征上既存在共性又有特性，而学生已经掌握了轴对称、平移的特征，旋转是三种变换中难度较大的一种，图形也比较复杂，因此，学生对旋转图形的形成过程的理解仍会有一定的困难。

教学目标知识技能：能够按要求作出简单平面图形旋转后的图形。

数学思考：经历对具有旋转特征的图形进行观察、分析、动手操作和画图等过程，掌握画图技能。

问题解决：对具有旋转特征的图形进行观察、分析、画图过程中，进一步发展学生的创新意识.情感态度：通过旋转作图，培养学生的审美意识教学方法与媒体采用自主探索，合作交流的学习方法。

合理利用多媒体课件教学过程复备第一环节：回顾旧知1.什么是平移？什么是旋转？图形的旋转有什么性质？2．下列一组图形变换属于旋转变换的是（）3．如图，ΔABC和ΔADE均为正三角形，则图中可看作是旋转关系的三角形是( )A．ΔABC和ΔADE B．ΔABC和ΔABDC．ΔABD和ΔACE D．ΔACE和ΔADE4．对下图中图案的形成过程叙述正确的是（）．A．它可以看作是一只小狗绕图案的中心位置旋转90°，180°，270°形成的B．它可以看作是相邻两只小狗绕图案的中心位置旋转180°形成的EDB CAC ．它可以看作是相邻两只小狗绕图案的恰当的对称轴翻折而成的D ．它可以看作是左侧、上面的小狗分别向右侧、下方平移得到的3．4.5. ΔABC 是等腰直角三角形，其中∠C 是直角， 将ΔABC 绕 着A 点逆时针旋转45°，旋转前后的图形组成图1；再将图1作为“基本图形”绕着A 点经过逆时针连续旋转得到图2．三次旋转的角度分别为（ ）．图1 图2A ．90°，180°，270°B ．90°，45°，180°C ．60°，30°，90°D ．30°，60°，180°6．如图，所给的图案可以看作ΔABC 绕点O 顺时针旋转( )前后的图形组成的．A ． 45°，90°，135°B ． 90°，135°，180°C ． 45°，90°，135°，180°，225°D ． 45°，135°，225°，270°第二环节：探索新知 1. 大家来看一面小旗子(出示小旗子，然后一边演示一边叙述)，把这面小旗子绕旗杆底端旋转90°后，这时小旗子的位置发生了变化，形成了新的图案，你能把这时的图案画出来吗？作图的一个要点：找图形的关键点。

课时课题：第三章 第四节 简单的旋转作图课型：新授课授课时间： 2012年 10 月 23日，星期 二，第三 节课教学目标：1.对具有旋转特征的图形进行观察、分析、画图和动手操作等过程，掌握画图技能.2.能够按要求作出简单平面图形旋转后的图形.3.通过画图，进一步培养学生的动手操作能力.教法及学法指导：学生已对轴对称、平移这两种简单的全等变换有了很好的认识，并对旋转有了初步的了解。

教材将旋转变换安排至此，目的是力求让学生从动态的角度观察图形、分析问题，为将来掌握 “全等”知识奠定基础。

本节课的主要内容是通过实例进一步认识旋转变换，探索、理解旋转的特征，并应用旋转的特征作图、解决简单的图形问题。

本节课的重难点是简单平面图形旋转后的图形的作法.课前准备：制作课件，学生课前复习尺规作图及预习工作.教具：小旗子、三角形、直尺、圆规教学过程:一、创设情境，导入新课师：上节课我们探讨了生活中的旋转，那什么样的运动是旋转呢？旋转有什么性质呢生：（复习后）积极举手回答。

师: 下列一组图形变换属于旋转变换的是（ ）生：（朱先富）C师:大家来看一面小旗子(出示小旗子，然后一边演示一边叙述)，把这面小旗子绕旗杆底端旋转90°后，这时小旗子的位置发生了变化，形成了新的图案，你能把这时的图案画出来吗？生：（小组讨论后画出）派一名学生（张晗）上台画出。

师:在原图上找了四个点，即O点、A点、B点、C点，如图(教师把该生所画的图在投影上放影)这四个点可以是能表示这面小旗子的关键点.因为旋转前后两个图形的对应点到旋转中心的距离相等，对应点与旋转中心的连线所组成的旋转角彼此相等，所以根据已知：要把这面小旗绕O 点按顺时针旋转90°.我在方格中找到点A、B、C的对应点A′、B′、C′，然后连接，就得到了所求作的图形.同学们在作图过程中，基本掌握了作图的一个要点：找图形的关键点。

这面小旗子是结构简单的平面图形，在方格纸上大家能画出它绕点旋转后的图形，那么在没有方格纸或旋转角不是特殊角的情况下，能否也画出简单平面图形旋转后的图形呢？这节课我们就来研究：简单的旋转作图.二、观察操作、探索归纳旋转的作法⑴观察、作图师:先利用多媒体逐一演示点、线段、多边形的旋转。