数学分析课后习题答案--高教第二版(陈纪修)--11章

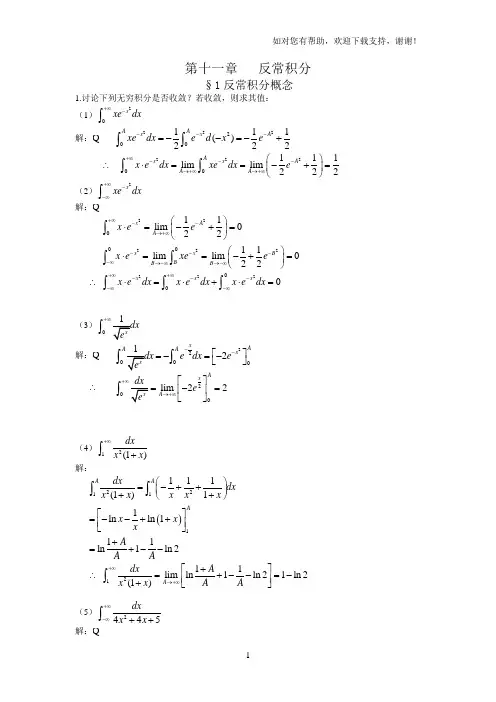
第十一章 反常积分§1反常积分概念1.讨论下列无穷积分是否收敛？若收敛，则求其值： （1）2x xe dx +∞-⎰解：222200111()222AA x x A xe dx e d x e ---=--=-+⎰⎰ ∴ 22200111lim lim 222A x x A A A x e dx xe dx e+∞---→+∞→+∞⎛⎫⋅==-+= ⎪⎝⎭⎰⎰ （2）2x xe dx +∞--∞⎰解：2222200011lim 02211lim lim 022x A A x x B B B B x e e x e xe e +∞--→+∞----∞→-∞→-∞⎛⎫⋅=-+= ⎪⎝⎭⎛⎫⋅==-+= ⎪⎝⎭⎰⎰⎰ ∴ 2220x x x x e dx x e dx x e dx +∞+∞----∞-∞⋅=⋅+⋅=⎰⎰⎰（3）0+∞⎰解：22002xAAA x e dx e --⎡⎤=-=-⎣⎦⎰⎰∴2l i m 22AxA e →+∞+∞⎡⎤-=⎢⎥⎣⎦=⎰（4）21(1)dxx x +∞+⎰解：()22111111(1)11ln ln 111ln 1ln 2AA Adx dx x x x x x x x x A A A ⎛⎫=-++ ⎪++⎝⎭⎡⎤=--++⎢⎥⎣⎦+=+--⎰⎰ ∴ 21lim 11ln 1ln 21ln 2(1)A dx A x x A A →+∞+∞+⎡⎤=⎢⎥=+--⎣-⎦+⎰ （5）2445dxx x +∞-∞++⎰解：2202001445(21)lim lim 1lim arcta 2(2n 1)82AA A A AA dx x x x x π→+∞→+∞→+∞==+++++=⎰⎰2220001445(21)2(21)l i m l i m 1l i m a r c t a n 41l i m a r c t a 1)48n(2B B B B B B Bdx dx x x x x B π→-∞→-∞→-∞→-∞=+++++=+=⎡⎤-=⎢⎥⎣⎦⎰⎰ ∴ 002224454454l i m l m 4i 5884A B A B dx dx dxx x x x x x πππ→++∞-→∞∞-∞=+++++=+=++⎰⎰⎰（6）0sin x e xdx +∞-⎰解：()0sin sin 1sin co limim s l 22AxA x x A A e xdx e xdxe x x →+∞→++---∞∞==--=⎰⎰（7）sin x e xdx +∞--∞⎰解：limsin sin AA x x e xdx e xdx →++∞∞=⎰⎰0sin limcos 2AA x x →+∞-= ()1sin lim cos 12A A A →+∞=-+发散 而limsin sin B xx Be xdx e xdx →∞--∞⋅=⎰⎰0sin limcos 2BB x x →-∞-=发散∴sin x e xdx +∞--∞⎰发散（8）+∞⎰解：0limli m A A A A →+∞→+∞=⎰发散故+∞⎰2. 讨论下列瑕积分是否收敛？若收敛，则求其值：（1）()bp a dxx a -⎰解：()21()f x x a =-在(,]a b 上连续， 从而在(,]a b 上可积，x a =为其瑕点由瑕积分定义，知111lim()()lim ()()1lim ()11lim ()()1bb p pau u a bp uu a p bu u a p pu a dx dx x a x a x a d x a x a pb a u a p →-→-→--→=--=--=--⎡⎤=---⎣⎦-⎰⎰⎰显然当1p <时，上式收敛于1()1pb a p---，其瑕积分也收敛，其值为1()1pb a p---若1p ≥，则上式发散，其瑕积分也发散（2）1201dx x -⎰解：122001010010011lim 11111lim 211111lim 21111lim ln 1ln 12211lim ln 1ln 122u u u u u u u u u u u dxdx x x dx x x dx dx x x x x u u →→→→→=--⎛⎫=+ ⎪-+⎝⎭⎡⎤=+⎢⎥-+⎣⎦⎧⎫=-⎡-⎤+⎡+⎤⎨⎬⎣⎦⎣⎦⎩⎭⎡⎤=--++⎢⎥⎣⎦⎰⎰⎰⎰⎰ 上式的极限不存在，故瑕积分1201dxx -⎰发散（3）2⎰解：()()()()()()212001112221111222011112211lim 1lim 1lim 21lim 21lim 212lim 2214uuu u u uu u u u x dx x dxx x u u --→→--→→--→→=+=-+-⎡⎤=--+-⎢⎥⎣⎦⎡⎤⎡⎤=--++--⎢⎥⎢⎥⎣⎦⎣⎦=⎰⎰⎰⎰⎰故瑕积分收敛，其值为4 （4）1⎰解：()()()()())11122201222112201111121lim 1121lim 12lim11u u uu u x d x x d x x --→-→→=---=---=--=-=⎰⎰⎰ 故瑕积分收敛，其值为1 （5）1ln xdx ⎰解：()111100ln lim ln lim ln lim ln 11u u u u u u xdx xdxx x dx u u u +++→→→=⎡⎤=-⎢⎥⎣⎦=--+=-⎰⎰⎰故瑕积分收敛，其值为-1（6）⎰解：令21xt x=-，则()20200020202lim 1lim 21lim arctan 12tdt t t t t t εεεπ+++→→→=+⎡⎢=⎢+⎣⎦⎛=- +⎝=⎰故瑕积分收敛，其值为2π（7）1⎰解：()()()()1111121211210200lim lim lim arcsin 21lim arcsin 21lim arcsin 21lim arcsin 21122x x εεεεεεεεεεεεπππ++++++-→→-→→→→==+=-+-=--+---⎡⎤⎡⎤⎣⎦⎣⎦=+=⎰⎰⎰⎰故瑕积分收敛，其值为π （8）10ln (ln )p d x x ⎰解：()()1112100211210211112100211100ln (ln )ln (ln )ln (ln )lim (ln 2)ln lim (ln )ln 11lim (ln )lim (ln )11111lim ln ln lim ln 1121p p p p p p p p p d x x d x x d x x d x x d xx x ppp p εεεεεεεεεεεε++++++-----→→---→→---→→=+=+=+--⎡⎤⎛⎫=-+-⎢⎥ ⎪--⎝⎭⎢⎥⎣⎦⎰⎰⎰⎰⎰11ln 2pp -⎡⎤⎛⎫-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦上面极限式发散，故瑕积分发散3. 举例说明：瑕积分⎰badx x f )(收敛时，⎰badx x f )(2不一定收敛。

陈纪修数学分析答案【篇一：陈纪修教授《数学分析》九讲学习笔记与心得】class=txt>云南分中心 ? 昆明学院 ? 周兴伟此次听陈教授的课，收益颇多。

陈教授的这些讲座，不仅是在教我们如何处理《数学分析》中一些教学重点和教学难点，更是几堂非常出色的示范课。

我们不妨来温习一下。

第一讲、微积分思想产生与发展的历史法国著名的数学家h.庞加莱说过：“如果我们想要预见数学的将来，适当的途径是研究这门科学的历史和现状。

” 那么，如果你要学好并用好《数学分析》，那么，掌故微积分思想产生与发展的历史是非常必要的。

陈教授就是以这一专题开讲的。

在学校中，我不仅讲授《数学分析》，也讲授《数学史》，所以我非常赞同陈教授在教学中渗透数学史的想法，这应该也是提高学生数学素养的有效途径。

在这一讲中，陈教授脉络清晰，分析精当，这是我自叹不如的。

讲《数学史》也有些年头，但仅满足于史料的堆砌，没有对一些精彩例子加以剖析。

如陈教授对祖暅是如何用“祖暅原理”求出球的体积的分析，这不仅对提高学生的学习兴趣是有益的（以疑激趣、以奇激趣），而且有利于提高学生的民族自豪感（陈教授也提到了这一点）。

第二讲、实数系的基本定理在这一讲中，陈教授从《实变函数》中对集合基数的讨论展开，对实数系的连续性作了有趣的讨论。

首先是从绅士开party的礼帽问题，带我们走进了“无穷的世界”。

我在开《数学赏析》时有一个专题就是“无穷的世界”，我给学生讲礼帽问题、也讲希尔伯特无穷旅馆问题，但遗憾的是，当我剖析“若无穷旅馆住满了人，再来两个时，可将住１号房间的移往３号房间，住２号房间的移往４号房间，从而空出两个房间”时，学生对我“能移”表示怀疑。

这一点我往往只能遗憾的说“跳不出有限的圈子，用有限的眼光来看无限，只能是‘只在此山中，云深不知处’”。

当然，我还是会进一步考虑如何来讲好这一讲。

若陈教授或其他老师有好的建议，能指点一下，则不胜感激。

对于集合[0,1]与(0,1)的对等关系，包括q与Ｒ的对等关系，或者说他们之间双射的构造。

第11章Euclid空间上的极限和连续一、判断题1．若f（x，y）在D内对x和y都是连续的，则f（x，y）对（x，y）∈D为二元连续函数．[重庆大学研]【答案】错【解析】举反例：，很明显但是不存在，如果选取路径y=kx趋于0，有不唯一．二、填空题（1）函数的定义域是______，它是______区域；（2）函数的定义域是______；（3）函数的定义域是______；（4）二元函数的定义域是______；（5）函数的定义域是______．[西安交通大学研]【答案】（1）（2）（3）椭圆与抛物线所围的区域；（4）（5）三、解答题1．设f（x）为定义在上的连续函数，α是任意实数，有证明：E是开集，F是闭集．[江苏大学2006研]证明：对任意的，有．因为f（x）在上连续，所以由连续函数的局部保号性知，存在的一个邻域使得当时有，从而，故E是开集．设为F 的任意一个聚点，则存在F中的点列使得．由于f（x）在上连续，所以，又，从而，即，故F是闭集．2．求．[南京大学研、厦门大学研、山东科技大学研]解：方法一由于令，有所以方法二由于，，所以，故有3．设f（x，y）在[a，b]×[c，d]上连续，证明：在[c，d]上连续．[南京理工大学研、华东师范大学研]证明：反证法．假设g（y）在某点处不连续，则存在及点列，使得因为f（x，y）在[a，b]×[c，d]上连续，故在[a，b]×[c，d]上一致连续．于是对，存在δ＞0，当时恒有．特别当时，即．固定y，让x在[a，b]上变化，取最大值，可得即时，．因为，所以对δ＞0，存在N ＞0，当n＞N时有，从而有，这与一开始得到的不等式矛盾，结论得证．4．设，为有界闭集，试证：开集W、V，使得A证明：A、B为有界闭集．[四川大学研]令显然W、V为开集．5．设试讨论下面三种极限：[南京工学院研]解：由于在y=0和x=0的函数极限不存在，故在（0，0）点的两个累次极限都不存在．6．设f（x，y是区域D：|x|≤1，|y|≤1上的有界k次齐次函数（k≥1），问极限是否存在？若存在，试求其值．[南京大学研]解：令x=rcosθ，y=rsinθ．由于f（x，y）是区域D上的有界k次齐次函数7．设二元函数f(x,y)在正方形区域[0，1]×[0，1]上连续．记J=[0，1]．（1）试比较的大小并证明之；（2）给出并证明使等式成立的（你认为最好的）充分条件．[浙江大学研]解：（1），有上式对于任意的x都成立，则由y的任意性可知（2）若，使下面证明上面条件为充分条件显然8．设为n维欧氏空间，A是的非空子集，定义x到A的距离为证明：上的一致连续函数．[南京大学研] 证明：有对使故对时，即上的一致连续函数．9．[暨南大学2013研] 解：设，则。

数学分析原理答案数学分析原理答案【篇一：数学分析教材和参考书】：《数学分析》（第二版），陈纪修，於崇华，金路编高等教育出版社, 上册：2004年6月，下册：2004年10月参考书：（1）《数学分析习题全解指南》，陈纪修，徐惠平，周渊，金路，邱维元高等教育出版社, 上册：2005年7月，下册：2005年11月（2）《高等数学引论》（第一卷），华罗庚著科学出版社（1964）（3）《微积分学教程》，菲赫金哥尔兹编，北京大学高等数学教研室译，人民教育出版社（1954）（4）《数学分析习题集》，吉米多维奇编，李荣译高等教育出版社（1958）（5）《数学分析原理》，卢丁著，赵慈庚，蒋铎译高等教育出版社（1979）（6）《数学分析》，陈传璋等编高等教育出版社（1978）（7）《数学分析》（上、下册），欧阳光中，朱学炎，秦曾复编，上海科学技术出版社（1983）（8）《数学分析》（第一、二、三卷），秦曾复，朱学炎编，高等教育出版社（1991）（9）《数学分析新讲》（第一、二、三册），张竹生编，北京大学出版社（1990）（10）《数学分析简明教程》（上、下册），邓东皋等编高等教育出版社（1999）（11）《数学分析》（第三版，上、下册），华东师范大学数学系，高等教育出版社（2002）（12）《数学分析教程》常庚哲，史济怀编，江苏教育出版社（1998）（13）《数学分析解题指南》林源渠，方企勤编，北京大学出版社（2003）（14）《数学分析中的典型问题与方法》裴礼文编，高等教育出版社（1993）复旦大学数学分析全套视频教程全程录像,asf播放格式，国家级精品课程，三学期视频全程教师简介:陈纪修-基本信息博士生导师教授姓名：陈纪修任教专业：理学-数学类在职情况：在性别：男所在院系：数学科学学院陈纪修-本人简介姓名：陈纪修性别：男学位：博士职称：教授（博士生导师）高校教龄22年，曾获2001年上海市教学成果一等奖、获2001年国家级教学成果二等奖、获2002年全国普通高等学校优秀教材一等奖、2002年获政府特殊津贴；获宝钢教育奖（优秀教师奖）；被评为“九五”国家基础科学人才培养基金实施和基地建设先进工作者。

数学分析第二版答案LtD数学分析第二版答案【篇一：?数学分析?第三版全册课后答案(1)】class=txt>------------------------------------------------- 密---------------------------------- 封----------------------------- 线---------------------------------------------------------第页(共)------------------------------------------------- 密---------------------------------- 封----------------------------- 线---------------------------------------------------------【篇二：复旦大学数学分析课后习题解陈纪修】> 4．〔1〕?x|?2?x?3?；〔2〕?(x,y)|x?0且y?0?；〔3〕?x|0?x?1且x?q?；〔4〕?x|x?k2,k?z?.?7．〔1〕不正确。

x?a?b?x?a或者x?b；〔2〕不正确。

x?a?b?x?a并且x?b.第2节2．〔1〕f:[a,b]?[0,1] x?y?x?ab?a.〔2〕f:(0,1)?(??,??) x?tan[x(?12)?]3．〔1〕y?log2a(x?3)，定义域：,?33,，值域：(??,??)；〔2〕y?arcsin3x，定义域：,0?，值域：???0,??；2??〔3〕y?tanx，定义域：k?k?z?2,k2?，值域：??0,；〔4〕y?x?1x?1，定义域：,?11,，值域：?0,11,. 5．〔1〕定义域：??2k?,(2k?1)??，值域：,0?；k?z〔2〕定义域：?2k??,2k，值域：?0,1?；k?z?22?1〔3〕定义域：??4,1?，值域：0,；?25??32 〔4〕定义域：,00,，值域：?,???2??. ??7．〔1〕f(x)?2x3?21x2?77x?97；〔2〕f(x)?2x?14x?1。

第十章 函数项级数习 题 10. 1 函数项级数的一致收敛性1. 讨论下列函数序列在指定区间上的一致收敛性。

⑴ S n (x ) = , (i) x nx −e ∈)1,0(， (ii) x ∈； ),1(+∞ ⑵ S n (x ) = x , x nx −e ∈),0(+∞；⑶ S n (x ) = sin nx , (i)x ∈),(+∞−∞， (ii) x ∈],[A A −()； 0>A ⑷ S n (x ) = arctan nx , (i)x ∈)1,0(， (ii) x ∈； ),1(+∞ ⑸ S n (x ) =221nx +, x ∈),(+∞−∞； ⑹ S n (x ) = nx (1 - x )n , x ∈]1,0[；⑺ S n (x ) =n x ln n x, (i) x ∈)1,0(， (ii) x ∈)；),1(+∞ ⑻ S n (x ) = nnx x +1, (i) x ∈)1,0(， (ii) x ∈；),1(+∞ ⑼ S n (x ) = (sin x )n , x ∈],0[π；⑽ S n (x ) = (sin x )n1, (i) x ∈[0,]π， (ii) x ∈],[（0>δ）；δπδ− ⑾ S n (x ) = nn x ⎟⎠⎞⎜⎝⎛+1, (i) x ∈),0(+∞， (ii)x ∈],0(A ()； 0>A ⑿ S n (x ) = ⎟⎟⎠⎞⎜⎜⎝⎛−+x n x n 1, (i) x ∈),0(+∞, (ii)[)0,,>+∞∈δδx 。

解 （1）(i) ，0)(=x S )()(sup ),()1,0(x S x S S S d n x n −=∈1= ─/→ 0（∞→n ）， 所以{}()n S x 在上非一致收敛。

(0,1) (ii) ，0)(=x S )()(sup ),(),1(x S x S S S d n x n −=+∞∈n e −=)(0∞→→n ，所以{}()n S x 在上一致收敛。

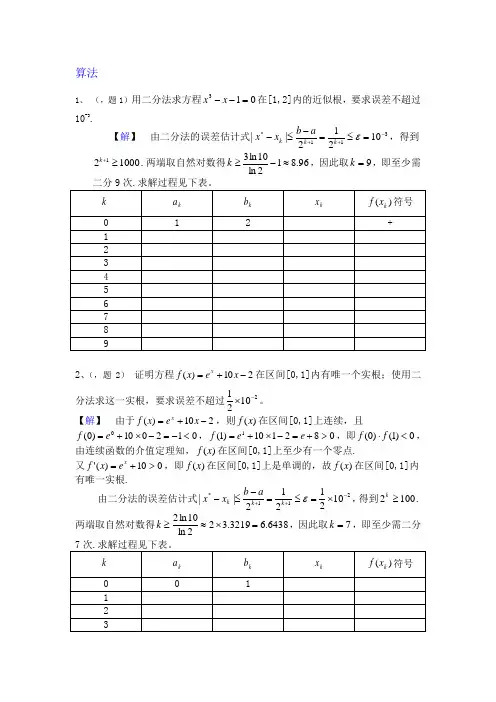
算法1、 （，题1）用二分法求方程013=--x x 在[1,2]内的近似根，要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ，得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ，因此取9=k ，即至少需2、（，题2） 证明方程210)(-+=x e x f x在区间[0,1]内有唯一个实根；使用二分法求这一实根，要求误差不超过21021-⨯。

【解】 由于210)(-+=x e x f x ，则)(x f 在区间[0,1]上连续，且012010)0(0<-=-⨯+=e f ，082110)1(1>+=-⨯+=e e f ，即0)1()0(<⋅f f ，由连续函数的介值定理知，)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ，即)(x f 在区间[0,1]上是单调的，故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ，得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ，因此取7=k ，即至少需二分误差1．（，题8）已知e=…，试问其近似值7.21=x ，71.22=x ，x 2=，718.23=x 各有几位有效数字？并给出它们的相对误差限。

【解】有效数字：因为11102105.001828.0||-⨯=<=-K x e ，所以7.21=x 有两位有效数字； 因为12102105.000828.0||-⨯=<=-K x e ，所以71.22=x 亦有两位有效数字；因为3310210005.000028.0||-⨯=<=-K x e ，所以718.23=x 有四位有效数字；%85.17.205.0||111=<-=x x e r ε； %85.171.205.0||222=<-=x x e r ε； %0184.0718.20005.0||333=<-=x x e r ε。

数学分析讲义答案【篇一：学习数学分析的一些建议和书籍】本帖最后由 ke.xigui 于 2009-5-21 21:49 编辑首先，只是觉得这篇东西写得很好，对学习数学分析的人可能有帮助，所以粘上来。

希望作者莫见怪。

旧版网站里许多有用的东西，但是现在找不到了，实在很可惜。

数学专业参考书整理推荐学数学要多看书，但是初学者很难知道那些书好，我从网上收集并结合自己的经验进行了整理：从数学分析开始讲起：数学分析是数学系最重要的一门课，经常一个点就会引申出今后的一门课，并且是今后数学系大部分课程的基础。

也是初学时比较难的一门课，这里的难主要是对数学分析思想和方法的不适应，其实随着课程的深入会一点点容易起来。

当大四考研复习再看时会感觉轻松许多。

数学系的数学分析讲三个学期共计15学分270学时。

将《数学分析》中较难的一部分删去再加上常微分方程的一些最简单的内容就是中国非数学专业的《高等数学》，或者叫数学一的高数部分。

记住以下几点：1，对于数学分析的学习，勤奋永远比天分重要。

2，学数学分析不难，难得是长期坚持做题和不遗余力的博览群书。

3，别指望第一遍就能记住和掌握什么，请看第二遍，第三遍，…,第阿列夫遍。

4，看得懂的仔细看，看不懂的硬着头皮看。

5，课本一个字一个字的看完，至少再看一本参考书，尽量做一本习题集。

6，开始前三遍，一本书看三遍效果好于三本书看一遍；第四遍开始相反。

7，经常回头看看自己走过的路以上几点请在学其他课程时参考。

数学分析书：初学从中选一本教材，一本参考书就基本够了。

我强烈推荐11，推荐1，2，7，8。

另外建议看一下当不了教材的16，20。

中国人自己写的：1《数学分析》陈传璋，金福临，朱学炎，欧阳光中著（新版作者顺序颠倒）应该是来自辛钦的《数学分析简明教程》，是数学系用的时间最长，用的最多的书，大部分学校考研分析的指定教材。

我大一用第二版，现在出了第三版，但是里面仍有一些印刷错误，不过克可以一眼看出来。

第十一章 广义积分§11.1 无穷限广义积分1. 求下列无穷积分的值： （1）⎰+∞-2211dx x ； （2）⎰+∞+22)1(1dx x x ；（3）)0(02>⎰+∞-a dx xe ax ；（4）)0(sin 0>⎰+∞-a bxdx eax；. （5）⎰∞++021dx x x； （6）)0,()()(022>+++⎰+∞q p q x p x dx．解 （1）3ln 21)31ln 11(ln 21lim 11lim 112222=-+-=-=-+∞→+∞→+∞⎰⎰A A dx x dx x A A A ． （2）2ln 21)2ln 1(ln 21lim )1(1lim )1(1221212=++=+=++∞→+∞→∞+⎰⎰AA dx x x dx x x A A A ． （3）a211a 21limlim222=-==-+∞→-+∞→+∞-⎰⎰）（e dx e x dx ex ax A Aax A ax ． （4）设⎰+∞-=0sin bxdx e I ax )0(>a ，则)cos sin 1(lim sin lim 000⎰--+∞→-+∞→+-=⎰=A ax A ax A Aax A dx bx e a b bx e a bxdx e I)sin cos (lim 002⎰--+∞→+-=A ax A axA bxdx e b bx e a bI ab a b bxdx eab a b bxdx e a b a b axA axA 22202220222sin sin lim -=-=-=⎰⎰∞+--+∞→，所以 ，22ba bI +=． （5）作变换y x =，则有⎰+++-+--++=+=+⎰⎰dy y y y y y y y y y y dy y y dx x x )21)(21()21(22)21(221212222422 ⎰⎰-+++-+-=)22(21)(2121)21(42222y y d y y y y d ⎰⎰+++++++-)22(2121)21)21(42222y dyy y y y d C y y y y y y +++-++++-=)]12arctan()12[arctan(222121ln 4222C x x x x x xy +++-+++-=)]12arctan()12[arctan(221)21(ln 4222， 所以，)]12arctan()12[arctan(221)21(ln 421222++-+++-=+⎰A A A A A dx x x A)(22)22(22+∞→=+→A πππ，即，π22102=+⎰∞+dx xx ． (6) 由于当q p =时，用⎰+=n n x a dxI )(22的地推公式，p x dxp p x x p p x dx q x p x dx +++=+=++⎰⎰2222222121)())((C pxp p p x x p +++=arctan 21212所以，时，0>=q ppp p A p p p A A p p x dx A AA 4)arctan 2121(lim )(lim2022π=++=++∞→+∞→⎰， 当q p ≠时，由于⎰⎰⎰+-+-=++--=++dx p x q x q p q x p x dx q p q p q x p x dx )11(1))(()(1))((222222C pxp q x q q p +--=)arctan 1arctan 1(1， 所以，当q p ≠时，⎰⎰+=+++∞→+∞A A q x dx q x p x dx 02022)(lim ))(( )(2)arctan 1arctan 1(1limq p pq p A p q A q q p A +=--=+∞→π两种情况下，即只要0,>q p ，就有⎰+∞+=++022)(2))((q p pq q x p x dx π． 2. 讨论下列积分的收敛性： （1）⎰+∞+0341x dx ；（2）⎰+∞+031arctan dx x x；（3）⎰∞＋121sindx x；（4）⎰+∞+０dx xx sin 11；（5）⎰+∞+022sin 1dx xx x； （6）)0,(10>+⎰∞+m n dx xx nm； （7）⎰∞++-０　1242x x dxx ；（8）⎰+∞+13211dx xx ；（9）)0(02≥⎰+∞-p dx e x x ；（10）⎰+∞1ln dx x xp； （11）⎰∞+12ln dx x xn （n 是正整数）； （12）⎰∞+02sin dx xx； （13）⎰+∞+01cos dx x axn ； （14）⎰+∞+-+1]11)11[ln(dx x x ；（15）⎰+∞+1)1sin 1ln(cos dx xx ；（16）⎰∞+-⎪⎪⎭⎫ ⎝⎛-０dx x x 1222sin 1ln 1． 解 （1）111lim 3434=++∞→x xx ，所以积分⎰+∞+0341x dx 收敛．（2）21arctan lim 32π=++∞→x x x x x ，故所求积分收敛．（3）111sin lim1sin lim 2222==+∞→+∞→x x xx x x ，因此所求积分收敛． （4）0≥∀x ，有011sin 11>+≥+x x x ，且+∞=+=+=++∞→+∞→+∞⎰⎰)1ln(lim 1lim 10A x dx x dxA A A ０，即⎰+∞+01xdx发散，由比较判别法知⎰+∞+０x x dx sin 1发散．（5）0≥∀x ，有01sin 1222>+≥+x x x x x ，而11lim 2=++∞→x xx x ，无穷积分⎰+∞+021dx x x 发散，由比较判别法知⎰+∞+022sin 1dx xx x发散． （6）因为11lim=++∞→nnx x x ，所以， 当1>-m n ，即1+>m n 时，⎰∞++01dx x x nm收敛；当1≤-m n ，即1+≤m n 时，⎰∞++01dx xx nm发散． （7）　11lim 2422=+-+∞→x x x x x ，所以积分收敛．（8）1111lim11lim 323235=+=++∞→+∞→x xx xx x ，所以积分收敛．（9） 因为 =+==++∞→++∞→-+∞→x px x p x xpx ex p e x e x x 122)2(lim lim )(lim 0])[()1)(2(lim ][=-++=-+∞→x p p x ex p p p p ， 所以无穷积分收敛．（10） 若1>p ，则可以选取00>ε，使得10>-εp ，由于0ln limln lim 0==+∞→-+∞→εεx xxx x X pp x ，所以⎰+∞1ln dx xxp 收敛； 若1≤p ，则当e x ≥时，p p x x x 1ln ≥，而⎰+∞11dx x p 发散，由比较判别法，⎰+∞1ln dx xx p 发散．从而，⎩⎨⎧≤>⎰∞+．时发散时收敛1p ,,1p ,ln 1dx x x p （11）由于012)1(22lim ln 2lim ln lim ln lim 2121121223=-⋅====+∞→-+∞→+∞→+∞→x n n x x n x x xx x x n x n x n x ， 所以无穷积分⎰∞+12ln dx x xn 收敛． （12） 因为xxx x x x x 22cos 2122cos 1sin 2-=-=，而 21)0sin 2(sin 212cos 0≤-=⎰A xdx A，对一切0>A 成立，x21在[1，+)∞单调下降，且当+∞→x 时趋于0，由Dirichlet 判别法⎰+∞122cos dx xx收敛，又⎰+∞12x dx 发散，所以⎰∞+02sin dx x x 发散（0=x 是可去间断点）． （13）当1>n 时，由于n nx x ax +≤+111cos ，而⎰+∞+011dx x n 收敛，所以⎰+∞+01cos dx xax n 收敛，故这时不论R a ∈是哪个常数，⎰+∞+01cos dx xaxn均绝对收敛． 当10≤<n 时，若0≠a ，则由于aaA a axdx A 1sin 1cos 0≤=⎰，而n x +11在),0[+∞单调递减，且当+∞→x 时趋于0，由Dirichlet 判别法知，无穷积分收敛，但由于)1(22cos )1(211cos 1cos 2nn n nx ax x x ax x ax +++=+≥+， 则由于⎰+∞+0)1(21dx x n 发散，同样由Dirichlet 判别法知⎰+∞+0)1(22cos dx x ax n 收敛，故⎰∞++021cos dx xax n 发散，由比较判别法知⎰∞++012cos dx x ax n 发散，故这时无穷积分条件收敛． 当10≤<n 且0=a 时，无穷积分为⎰+∞+011dx xn发散． 当0=n 时，无穷积分为⎪⎪⎩⎪⎪⎨⎧=+∞=≠==+∞→+∞→+∞→∞+⎰⎰,02A lim ,0sin 21lim 2cos lim 2cos A A 00a a aA adx ax dx ax A A ，不存在， 故这时，不论a 为何常数，积分发散．当0<n 时，若0=a ，无穷积分为⎰+∞+011dx x n发散．以下假设0≠a ，0820>=∃a πε，N K A ∈∃>∀,0，使得A a a k >-42ππ且142≤⎪⎪⎭⎫ ⎝⎛-na a k ππ，这时 0424282)44(421cos επππππππ==+≥+⎰+-a a a dx xax a a k aa k n， 由Cauchy 收敛原理，⎰+∞+01cos dx x axn 发散． 综上，积分⎰+∞+01cos dx x axn当0>n 时绝对收敛；当10≤<n 且0≠a 时条件收敛；其他时候发散．（14） 因为)1(21))1(11(1)1(21111)11ln(2222xo x x o x x x o x x x x +=+--+-=+-+，所以，⎰+∞+-+1]11)11[ln(dx xx 收敛．（15） 因为xx x xx x x x 1)1sin 1ln(cos lim)1sin 1ln(cos lim +=++∞→+∞→ 11sin1cos 1sin1cos lim )1)(1sin 1(cos )1(1cos )1(1sin lim222=+-=-+-+--=+∞→+∞→x x x x xx x x x x x x x ， 所以，⎰+∞+1)1sin 1ln(cos dx xx 发散．（16）因为12sin 1212≤-≤x ，所以，2ln 2sin 1ln 012≤⎪⎪⎭⎫⎝⎛-≤-x ．因此，21221222ln 2sin 1ln 12sin 1ln 1x x x x x ≤⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫⎝⎛---， 而⎰+∞122ln dx x 收敛，所以⎰∞+-⎪⎪⎭⎫⎝⎛-０dx x x 1222sin 1ln 1收敛（0=x 是可去间断点）． 3.讨论下列无穷积分的收敛性（包括绝对收敛或条件收敛）： （1）⎰∞+１dx xx2cos ； （2）⎰+∞１dx x xcos ； （3）⎰+∞1cos dx xx p ； （4）⎰∞++0100cos dx x xx ；（5）⎰+∞2sin ln ln ln xdx xx． 解 （1）xxx x x x x 22cos 2122cos 1cos 2+=+=， 由于⎰+∞121dx x 发散，而⎰+∞１dx xx 22cos 收敛（Dirichlet 判别法），因此，⎰∞+１dx x x 2cos 发散.（2）由Dirichlet 判别法知⎰+∞１dx xxcos 收敛，但由于x x x x 2cos cos ≥，而由(1)，⎰∞+１dx x x2cos 发散，故由比较判别法知⎰∞+1cos dx x x 发散，因而⎰+∞１dx xx cos 条件收敛.（3）1>p 时，由于p p x x x 1cos ≤对一切),1[+∞∈x 成立，所以⎰+∞1cos dx x x p绝对收敛．10≤<p 时，用Dirichlet 判别法知⎰+∞１dx xxp cos 收敛，但由于 pp p px x x x x x x 22cos 21cos cos 2+=≥，同样用Dirichlet 判别法知⎰+∞122cos dx x xp 收敛，而⎰+∞121dx x p 发散，故由比较判别法知⎰∞+1cos dx x x p发散，所以这时⎰+∞1cos dx x xp条件收敛． 0=p 时,⎰+∞1cos xdx 发散.0<p 时，亦发散(用Cauchy 收敛原理即可)．所以，⎰+∞1cos dx xxp 当1>p 时绝对收敛；10≤<p 时条件收敛；0≤p 时发散． （4）⎰⎰∞+∞++=+11100cos 100cos dx x x x x dx x x x ，由于⎰+∞1cos dx x x 收敛，100+x x 单调递减有界，故由Abel 判别法，⎰∞++1100cos dx x x x 收敛，从而⎰∞++0100cos dx x xx 也收敛，但)100(22cos )100(2100cos 100cos 2+++=+≥+x xx x x x x x x xx ，同样⎰∞++0)100(22cos dx x x x 收敛，但⎰∞++0)100(2dx x x发散，所以⎰∞++0100cos dx x x x 发散．因此，⎰∞++0100cos dx x xx 条件收敛．（5）⎰⎰+∞+∞=22ln ln ln ln sin sin ln ln ln dx x x x x xdx x x，用Dirichlet 判别法知⎰+∞2ln sin dx xx 收敛，而由于)(0ln ln ln +∞→→x xx ，因而xx ln ln ln 有界，且由于23)(ln 2ln ln 2ln ln ln x x xx x -=⎪⎪⎭⎫⎝⎛，当2e e x ≥小于零，故当2e e x ≥时，xx ln ln ln 单调递减，由Abel 判别法，⎰+∞2sin ln ln ln xdx xx收敛．但xx x x x x x x x x x ln 22cos )ln (ln ln 2ln ln sin ln ln ln sin ln ln ln 2-=≥， 同样用Abel 判别法，⎰∞+2ln 22cos ln ln dx xx x 收敛，而⎰∞+2ln 2ln ln dx xx 发散（当x 充分大时，xx x 1ln ln ln ≥），故⎰∞+22sin ln ln ln xdx x x 发散，由比较判别法，dx x x x ⎰∞+2sin ln ln ln 发散，无穷积分⎰+∞2sin ln ln ln xdx xx条件收敛． 4．设)()()(x g x h x f ≤≤，+∞<≤x a ，)(,x h 在任意有限区间],[A a 可积，又⎰+∞adx x f )(和⎰+∞adx x g )(收敛．求证⎰+∞adx x h )(收敛．证明 由于)()()(x g x h x f ≤≤，+∞<≤x a ，所以，)()()()(0x f x g x f x h -≤-≤，+∞<≤x a ，又⎰+∞adx x f )(和⎰+∞adx x g )(收敛，故⎰+∞-adx x f x g )]()([也收敛，因而由比较判别法，⎰+∞-adx x f x h )]()([收敛．而)()]()([)(x f x f x h x h +-=， 所以，dx x f x f x h dx x h aa⎰⎰+∞+∞+-=)}()]()({[)(收敛．5. 证明定理11.2，并举例说明其逆是不成立的．证明 定理11.2 若⎰+∞adx x f )(收敛，则⎰+∞adx x f )(收敛．证法1、由于⎰+∞adx x f )(收敛，有无穷限积分的Cauchy 原理，0A ,0>∃>∀ε，当A A A >''',时，有ε<⎰'''A A )(dx x f ，从而当A A A >''',时，有ε<≤⎰⎰''''''A A A A dx x f dx x f )()(，同样由无穷积分的Cauchy 收敛原理，知⎰+∞adx x f )(收敛．证法2、由于),[,)()()(∞+∈≤≤-a x x f x f x f ，由第4题结论知，⎰+∞adx x f )(收敛．其逆是不成立的．例如，3（2）题中积分⎰+∞１dx xxcos 收敛，但⎰∞+1cos dx x x 发散． 6. 若)(x f 在),[∞+a 上单调下降，且积分⎰+∞adx x f )(收敛，求证：0)(lim =+∞→x xf x ．证明 由于⎰+∞adx x f )(收敛，故依)(x f 在),[∞+a 上单调下降知，),[∞+∈∀a x ，有0)(≥x f ，否则，若),[0∞+∈∃a x ，使0)(0<x f ，则01x x >∀，有0)()(01<≤x f x f ，因而0x b >∀，有）+∞→∞-→-+≤+=⎰⎰⎰⎰b x b x f dx x f dx x f dx x f dx x f bax abx x a())(()()()()(000， 与⎰+∞adx x f )(收敛相矛盾．由无穷积分的Cauchy 收敛原理00>∃>∀A ，ε，当A A ,A >'''时，有2)(A A ε<⎰'''dx x f ，所以，当A 2>x 时，有2)(2ε<⎰xxdt t f ，由⎰<⇒<≤x x x xf dt t f x f x 2)(2)()(2εε，因此，0)(lim =+∞→x xf x ．7. 设)(x f 在),0[+∞上一致连续，并且积分⎰+∞)(dx x f 收敛．证明0)(lim =+∞→x f x ．如果仅仅知道积分⎰+∞)(dx x f 收敛，以及)(x f 在),0[+∞上连续，0)(≥x f ，是否仍有0)(lim =+∞→x f x ？证明 证法1、由)(x f 在),0[+∞上一致连续，0 0>∃>∀δε，（不妨设εδ≤），当),0[,21∞+∈x x ，δ≤-21x x 时，2)()(21ε<-x f x f ，又由⎰+∞)(dx x f 收敛，对上述0>δ，，0>∃N ，当N x x >21,时，有2)(221δ<⎰x xdx x f ．N x >∀，取N x x >21,，使得21x x x <<，且δ=-12x x ，则由⎰⎰⎰⎰+-==21212121)()()()()(x x x x x x x x dt t f dt t f dt x f dt x f x f δ22)()()(22121δδε+<+-≤⎰⎰x x x x dt t f dt t f x f ，所以，当N x >时，εδε≤+<22)(x f ，因此，0)(lim =+∞→x f x ．证法2、假设0)(lim ≠+∞→x f x ，则00>∃ε，0>∀A ，存在与A 有关的A x >0，使00)(ε≥x f ．不妨设00)(ε≥x f ，由)(x f 在),0[+∞上一致连续，0>∃δ，当a x x ≥''',，且δ<''-'x x 时，2)()(0ε<''-'x f x f ．故当),(00δδ+-∈x x x 时，2)()(00ε<-x f x f ，所以，22)()(00εε≥->x f x f ，因此δεδδ000)(≥⎰+-x x dx x f ，与⎰+∞)(dx x f 收敛矛盾，从而0)(lim =+∞→x f x ．如果仅仅知道积分⎰+∞)(dx x f 收敛，以及)(x f 在),0[+∞上连续非负，则0)(lim =+∞→x f x 不成立．例如⎪⎪⎩⎪⎪⎨⎧-++⋃∈===∞=+，其他线性,,]211,21[]21,0[,0,),2,1(,1)(11 n n n n n x n n x x f则121)(10==∑⎰∞=+∞n n dx x f ，即⎰+∞0)(dx x f 收敛，显然)(x f 在),0[+∞上连续非负，但)(lim x f x +∞→不存在．8. 设⎰+∞adx x f )(与⎰+∞'adx x f )(收敛，求证：0)(lim =+∞→x f x ．证明 由于⎰+∞'adx x f )(收敛，因而,))()((lim )(lim )('lima f x f t f dt t f x xa x xax -==+∞→+∞→+∞→⎰存在，因而)(lim x f x +∞→存在，设l x f x =+∞→)(lim ，若0≠l ，不妨设0>l ，则a A >∃0且00>A ，当0201,A A A A >>时，02)(>>lx f ．又⎰+∞a dx x f )(收敛，故0>∀ε，a A >∃1且01>A ，当11,A A A A >''>'时，有ε<⎰'''ＡＡdx x f )(．令},m ax {10A A A =，则当AA >'时，A A >'2，因此以下二式同时成立：ε<>'⎰''A A dx x f lA f 2)(,2)(．故022)(22>'=>⎰⎰''''A ldx l dx x f A A A A ， 所以，ε<'A l2，但这是矛盾的，因此0)(lim =+∞→x f x .9．设)(x f 单调下降趋于0, )(x f '在),0[∞+连续．求证：⎰+∞'02sin )(xdx x f收敛．证明⎰⎰⎰+∞→+∞→+∞='='AA AA x xdf xdx x f xdx x f 020202)(sin limsin )(limsin )(⎰⎰+∞+∞→=-=022sin )(]2sin )(sin )([lim xdx x f xdx x f A A f A A ，由于0>∀A ，1)12(cos 212sin 0≤--=⎰A xdx A，由Dirichlet 判别法，⎰+∞02sin )(xdx x f 收敛，因而⎰+∞'02sin )(xdx x f 收敛．10．设)(x f 和)(x g 是定义在),[∞+a 上的函数，且在任何有限区间],[A a 上可积．证明：若⎰+∞adx x f )(2与⎰+∞adx x g )(2收敛，则⎰+∞+adx x g x f 2)]()([与⎰+∞adx x g x f )()(也收敛．证明 由于)]()([21)()(22x g x f x g x f +≤及)()(x g x f 在任何有限区间],[A a 上可积，⎰+∞adx x f )(2与⎰+∞adx x g )(2收敛，由比较判别法知⎰+∞adx x g x f )()(收敛，因而⎰+∞adx x g x f )()(收敛．又)()()(2)()]()([222x g x g x f x f x g x f ++=+，所以⎰+∞+adx x g x f 2)]()([也收敛．11．证明：(1)设)(x f 在),0[∞+连续，且k x f x =+∞→)(lim ，则)0(ln ])0([)()(0>>-=-⎰+∞a b abk f dx x bx f ax f ； （2）若上述条件k x f x =+∞→)(lim 改为⎰+∞a dx xx f )(存在)0(>a ，则)0.(ln )0()()(0>>=-⎰+∞a b abf dx x bx f ax f ． 证明（1）当+∞<∆<<δ0时，积分 ⎰⎰⎰⎰⎰∆∆∆∆∆-=-=-b b a a dz zz f dz z z f dx x bx f dx x ax f dx x bx f ax f δδδδδ)()()()()()( ⎰⎰⎰⎰∆∆∆∆--=b a b a b a b a z dzf z dz f dz zz f dz z z f )()()()(ηξδδδδ ),(ln )(ln )(∆≤≤∆≤≤-=b a b a abf a b f ηδξδηξ，所以，⎰⎰∆+∞→∆+∞-=-δdx xbx f ax f dx x bx f ax f )()(lim )()(0ab f f a b f a b f ln )](lim )(lim [)ln )(ln)((lim 00ηξηξδδ+∞→∆→→+∞→∆-=-=++由于+→0δ时，+→0ξ；+∞→∆时，∞→＋η，所以abk f a b f f dx x bx f ax f ln ])0([ln )](lim )(lim [)()(0-=-=-+∞→∆→∆+⎰ηξδδ． (2) 用（1），当+∞<∆<<δ0时，有⎰⎰⎰∆∆∆-=-δδδb a b a dz zz f dz z z f dx x bx f ax f )()()()( )()(ln )(δξδξb a dz zz f a b f b a ≤≤-=⎰∆∆，令+∞→∆→+,0δ取极限，由于⎰+∞a dx x x f )(存在，故)(0)(+∞→∆→⎰∆∆b a dz zz f ，所以，abf dx x bx f ax f ln )0()()(0=-⎰+∞．§11.2 瑕积分1. 下列积分是否收敛？若收敛求其值． (1)⎰210cot xdx ；(2)⎰1ln xdx ；(3)⎰-axa dx 0；(4)⎰-11dx xx． 解 (1) +∞=-=++→→⎰)sin ln 21sin (ln lim cot lim 0210ηηηηxdx ，所以，⎰210cot xdx 发散．（2）1)1ln (lim )ln (lim ln lim 01101-=+--=-=+++→→→⎰⎰ηηηηηηηηηdx x x xdx ，所以⎰1ln xdx收敛, 且⎰-=11ln xdx ．（3）a a dt t t xa dx aa 2)(22lim lim 0=-=-=-⎰⎰++→-→ηηηηη，所以⎰-a xa dx0收敛，且⎰=-aa xa dx2． （4）ηηηηηηηη-→-→-→⎪⎭⎫ ⎝⎛+-=+=-+++⎰⎰1020102220101arctan lim )1(2lim 1lim t t t dt t t dx xx2)1(1arctanπηηηη=---=，所以dx x x ⎰-11收敛 ,且其值为2π． 2．讨论下列积分的收敛性: （1）dx xx ⎰123sin ；（2）⎰-1032)1(x x dx ；（3）⎰-1021ln dx x x；（4）⎰2022cos sin πx x dx； （5）⎰1ln dx x p；（6）⎰-20cos 1πdx xxm； （7）⎰10ln x dx ；（8）⎰πsin xdx ；（9）⎰1ln xdx xα；（10）⎰---111ln dx xx x q p ；（11）⎰20tan πdx x ； （12）⎰20sin ln cos πxdx x ．解（1）因为2123231sin xxx xx =≤，]1,0(∈∀x ，由dx x⎰11收敛及比较判别法,知 dx xx ⎰123sin 收敛．（2）⎰⎰⎰-+-=-12132210321032)1()1()1(x x dx x x dx x x dx ，]21,0(∈x 时,32332322)211(1)1(1xdxx x x =-≤-，由于⎰2103232dx x收敛，可得⎰-21032)1(x x dx 收敛 ；]1,21(∈x 时,33323214)1(211)1(1xdx x x x -=-⎪⎭⎫⎝⎛≤-，由于dx x⎰-2103314收敛，可得⎰-12132)1(x x dx 收敛，所以⎰-1032)1(x x dx 收敛．（3）⎰-1021ln dx x x 只有瑕点1,0==x x 是可去奇点．因为当210≤<x 时， x x x ln 341ln 2-≤-成立,故由比较判别法知⎰-1021ln dx x x收敛(绝对收敛)．（4）12sin 4lim cos sin 1lim 2202220==++→→x x x x x x x ，所以，⎰2022cos sin πxx dx 发散． （5）若0<p ，则由于)0(0ln +→→x x p知0=x 是可去间断点, 而1=x 是瑕点 ,这时由于)1()1(~)]1(1ln[ln -→--+=x x x xp pp，故当01<<-p 时，⎰1ln dx x p收敛，1-≤p 时，发散.若0=p ，则是常义积分11=⎰dx 存在．当0>p 时， 1=x 是可去间断点, 而0=x 是瑕点，由于0ln lim 21=+→px xx ，所以⎰1ln dx x p收敛．（6）mm x xx x 2sin 2cos 12=-， 当2≤m 时，+→0x 时该式极限为0或21存在，故这时0=x 不是瑕点，这是常义积分．当2>m 时， 由于21cos 1lim 20=--→+mm x x x x ，所以， 当12<-m 即32<<m 时，瑕积分⎰-2cos 1πdx x xm收敛，当12≥-m 即3≥m 时发散． （7）1ln 1)1(lim 1=---→xx x ，所以⎰10ln x dx 发散． （8）⎰⎰⎰+=ππππ22sin sin sin xdx x dx xdx ，因为1sin 1lim 210=+→xxx ， 1sin 1)(lim 21=--→xx x ππ，所以⎰20sin πxdx ，⎰ππ2sin xdx 均收敛，故⎰πsin xdx 收敛．（9）当0>α时，由于0ln lim 0=+→x x x α，故是常义积分．当0=α时，1))1(ln (lim ln lim ln 011-=---==++→→⎰⎰εεεεεεxdx xdx ，所以积分收敛．当01<<-α时 ，00>∃ε，使101000<+-<⇒->->εαεα，而()0ln lim ln lim 000=-=++→+-→x x x x x x x εαεα，所以，⎰1ln xdx xα收敛．当 1-≤α 时，+∞==++→-→x x x xx x ln lim ln lim 0αα，由1≥-α知，⎰1ln xdx x α发散．（10） 当q p =时被积函数为0，故积分值为0．由于在相差一个负号的意义下，qp ,对称，故可只考虑q p >的情形．这时，)1(ln ln 111-=-----qp q q p x xx x x x ，若1>q ，则0=x 不是瑕点，因而积分为常义积分，积分值存在． 若1<q ，则被积函数为)1(ln 11---qp qx xx ． ① 当11<-q 即0>q 时，故00>∃ε，使110<+-εq ，而⎰+-110εq x dx 收敛，xx ln 0ε单调增加（在)1,0(），且当+→0x 时趋于0，故由此得xx ln 0ε有界，因而由Abel 判别法知dx x x q ⎰-101ln 1收敛，又1--qp x 在)1,0(单调增加且有界，故知⎰---101)1(ln 1dx x xx q p q 即⎰---111ln dx xx x q p 收敛.② 当11>-q 即 0<q 时, 01>∃ε，使111>--εq ，因而)1(ln 11)1(ln 11111-=------q p q qp q x xx x x x x εε， 而 +∞=--→+)1(ln 1lim 10q p x x x x ε，故有10<<δ，当δ<<x 0时，1)1(ln 11>--qp x xx ε，因而1111)1(ln 1ε---->-q qp q xx x x ，所以积分 ⎰---1011ln dx x x x q p 发散． ③ 当11=-q 时，即0=q 时，由于当]21,0(∈x 时，0ln <x 而1121-≥-⎪⎭⎫⎝⎛--q p qp x ，故当]21,0(∈x 时，⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛≥---121ln 1)1(ln 1qp qp x x x x x ，由于 -∞=-==++→→⎰⎰)ln ln 2ln (ln lim ln 1lim ln 10210210εεεεdx xx dx x x发散，故由比较判别法，⎰--21)1(ln 1dx x xx qp 发散，因而⎰--10)1(ln 1dx x x x q p 发散．若1=q ，积分为⎰--10)1(ln 1dx x x qp ，这时0)1(ln 1lim 0=--→+q p x x x，故0=x 不是瑕点，积分是常义积分,因而存在．综上，瑕积分⎰---111ln dx xx x q p 当0>>q p 时收敛，q p >且0≤q 时发散；对称地，瑕积分⎰---111ln dx xx x q p 当0>>p q 时收敛，p q >而0≤p 时发散；q p =时，亦收敛．（11）解法1、令t x =tan ，则2tan t x =，2arctan t x =，dt ttdx 412+=，且当0=x 时，0=t ；2π=x 时，+∞=t ．瑕积分⎰⎰∞++=0422012tan dt tt dx x π化为了无穷积分．由于212lim 422=++∞→t t t t ， 故广义积分⎰∞++04212dt tt 收敛，即⎰20tan πdx x 收敛． 解法2、由于1sin )2sin()2(lim tan )2(lim 212212=--=---→→x x x x x x x πππππ，所以⎰20tan πdx x收敛．（12）由于0sin ln cos lim 0=+→x x x x ，故⎰20sin ln cos πxdx x 收敛．实际上，1)cos sin ln sin (lim sin ln cos lim sin ln cos 202020-=--==⎰⎰⎰++→→πεεπεεπεεxdx xdx x xdx x ．3.判别敛散性: (1)⎰∞+-⎪⎭⎫ ⎝⎛-12111ln dx x ； (2)⎰+∞--01dx e x x p ；(3)⎰∞+0)(arctan dx x x pq； (4)⎰+∞+0)1ln(dx xx p；(5)⎰+∞1ln x x dxq p ；(6)⎰+∞+0qp xx dx； (7)⎰+∞--032)2()1(x x x dx ；(8)⎰∞-0ln dx x e x ．解（1）⎰⎰⎰∞+--∞+-⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-221212112111ln 11ln 11ln dx x dx x dx x ，对⎰⎰∞+∞+-⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛-2222111ln 11ln dx x dx x ，由于122111lim )11ln(lim 33222=⋅-=⎥⎦⎤⎢⎣⎡--+∞→+∞→x x x x x x x ，所以，⎰∞+-⎪⎭⎫ ⎝⎛-22111ln dx x 收敛． 对⎰⎰⎰⎰--=--=⎪⎭⎫ ⎝⎛--2122121222121)1ln(ln 21ln 11ln dx x xdx dx x x dx x ，前一项为定积分，后一项以1=x 为瑕点．由于⎰⎰⎰-++=-2121212)1ln()1ln()1ln(dx x dx x dx x ，前一项为常义积分，而对后一项，由于0)1ln()1(lim 211=--+→x x x ，故⎰-21)1ln(dx x 收敛，因此⎰⎪⎭⎫ ⎝⎛--212111ln dx x 收敛，最后知道⎰∞+-⎪⎭⎫ ⎝⎛-12111ln dx x 收敛．（2）当1≥p 时，⎰+∞--01dx e x x p 是一无穷积分，收敛．当1<p 时，⎰⎰⎰+∞----+∞--+=111101dx e x dx e x dx e x x p x p x p ，后者为无穷积分收敛；对于前者，由于1)(lim 110=---→+x p px e x x，所以当11<-p ，即10<<p 时，⎰--11dx e x x p 收敛，当11≥-p ，即0≤p 时，⎰--11dx e xxp 发散．从而，当0>p 时，⎰+∞--01dx e x x p 收敛，当0≤p 时发散．（3）由于当0→x 时，x x →arctan ，所以当p q >时，pq pq x x x -~)(arctan ，)0(+→x ；p q =时，1)(arctan lim 0=+→pqx x x ．故当p q ≥时，上述积分只是无穷积分而无瑕点．若1>p 且p q ≥，由qpp q x x x ⎪⎭⎫⎝⎛≤21)(arctan π≤x p 1)2(πq，收敛；若10≤<p 且p q ≥，则由)1(1)(arctan ≥≥x xx x pp q ，发散； 若0=p 且p q ≥时，当x 充分大时，)1(1)(arctan ≥≥x xx pq这时无穷积分发散； 若0<p 且p q ≥时，显然发散．当p q <时，积分可分为⎰⎰∞++110)(arctan )(arctan dx x x dx x x p qp q ，对于前者，pqx x )(arctan 与qp x -1是同阶无穷大量，故当10<-<q p ，即1+<<q p q 时收敛，而当1≥-q p 即1+≥q p 时发散．对于后者，同样在1>p 时收敛，1≤p 时发散．综上，当1+<<q p q 且1>p 时积分收敛，当p q <而1≤p 时积分发散． 因此，当1>≥p q 或1+<<q p q 且1>p 时积分收敛，其他情况发散．即当11+<<q p 时积分收敛，其他情况积分发散．（4）⎰⎰⎰+∞+∞+++=+11)1ln()1ln()1ln(dx xx dx xx dx xx ppp，因为1)1ln(lim 1=+-→+xx x pp x ，故前一积分当11<-p 即2<p 时收敛，当2≥p 时发散．而对后一积分，若1>p ，则00>∃ε，使得10>-εp ，且0)1ln(lim 0=++∞→εxx x ，故当x 充分大时，001)1ln(1)1ln(εεε--<+=+p p p x x x x x x ，由比较判别法，积分收敛．当1≤p 时，x x x p1)1ln(≥+（1-≥e x 时），所以这时积分发散． 因此，当21<<p 时，原积分收敛，否则发散． （5）⎰⎰⎰+∞+∞+=2211ln ln ln xx dxx x dx x x dx q p q p q p ， 对于前者，因为0ln 1)1(lim 211=-+→xx x qp x ，故总是收敛的； 对于后者，1>p 或1=p 而1>q 时收敛，其他发散．故⎰+∞1ln x x dxq p 当1>p 或1=p 而1>q 时收敛，对于其他情况均发散．（6）⎰⎰⎰+∞+∞+++=+1100qp q p q p x x dx x x dx x x dx ， 若q p =，则前者要求1<=q p 收敛，后者要求1>=q p 收敛，故这时积分发散．由q p ,的对称性，只需考虑q p >的情况．对于前者由)1(11+=+-qp q q p x x x x ，故当1<q 时收敛，1≥q 时发散．而对于后者，由于)1(11p q p q p x x x x -+=+，故当1>p 时收敛，1≤p 时发散．故⎰+∞+0qp xx dx当1>p 且1<q 或1<p 且1>q 时收敛，其他情况下均发散． （7）⎰⎰⎰--+--=--∞+2321322103232)2()1()2()1()2()1(x x x dx x x x dx x x x dx⎰⎰+∞--+--+33232332)2()1()2()1(x x x dx x x x dx由于332321)2()1(lim =--+→x x x xx ， 1)2()1()1(lim32321=---→x x x x x ，33231221)2()1(2lim=---→x x x x x ， 1)2()1(1lim 3234=--+∞→x x x xx ，以上四个积分均收敛，故原积分收敛．（8）令t x =-，则-∞=x 时，+∞=t ，当0=x 时，0=t 仍记t 为x ．⎰⎰⎰⎰⎰+∞--+∞-∞+-∞-+==-=11ln ln ln ln ln xdx e xdx e xdx e xdx e dx x e x xxxx．由于当x 充分大时，21ln xx ex≤-，而⎰+∞121dx x 收敛，故⎰+∞-1ln xdx e x收敛，又0ln lim 0=-→+x e x x x ，故⎰-1ln xdx e x 亦收敛，所以⎰⎰+∞-∞-=00ln ln xdx e dx x e x x 收敛．4．讨论下列积分的收敛性与绝对收敛性： （1）⎰+∞2sin dx x ；（2）⎰∞+0sin dx x x q p，其中0>p ； （3）)0(1sin 0≥+⎰∞+q dx xxx qp ； （4）⎰∞++0)1sin(dx xx x n ． 解 （1）由于0sin lim 0=+→xx x ，所以0=x 不是瑕点，由Dirichlet 判别法，无穷积分⎰+∞sin dx xx 收敛，因此，⎰⎰⎰⎰+∞+∞→+∞→+∞→===00002sin 21sin lim 212sin limsin lim2dt ttdt t t t dtt dx x A A A A AA所以，⎰+∞2sin dx x 收敛．但xx xxx xx 22cos 21sin sin 2-=≥，由于⎰+∞121dx x发散，同样用Dirichlet 判别法知⎰+∞122cos dx xx 收敛，故⎰+∞-1)22cos 21(dx xx x发散，由比较判别法知⎰∞+1sin dx xx 发散，因而⎰∞+0sin dx xx 发散，但⎰⎰⎰+∞→+∞→+∞→==A A AA AA dt tt dt t tdx x 002sin lim 212sin limsin lim不存在，故⎰+∞2sin dx x 发散，因而⎰+∞2sin xdx 条件收敛．（2）⎰⎰⎰∞+∞++=1100sin sin sin dx xx dx x x dx x x q pq p q p，先考虑⎰10sin dx x x q p ，由于pp x x ~sin )0(+→x ，所以q p x x sin 与p q x-1是同阶变量)0(+→x ，从而当1<-p q 时，即1+<p q 时该积分收敛，1+≥p q 时积分发散．且由于0sin ≥qpxx ，故是绝对收敛的． 再看⎰⎰⎰∞+-+∞+-∞+==1111111sin 11sin sin dt xtp dt t p x t x t dx x x pq p p q pqp ，故当011>-+p q 时，即1>+p q 时积分收敛，否则发散．且当1>q 时绝对收敛，11≤<-q p 条件收敛．所以当p q p +<<-11时，积分收敛，否则发散． 当p q +<<11时绝对收敛，11≤<-q p 时条件收敛．（3）⎰⎰⎰∞+∞++++=+11001sin 1sin 1sin dx xx x dx x x x dx x xx q pq p q p ， 先考虑积分⎰+11sin dx x x x q p ，由于111sin lim 1sin lim 010=+=+++→--→q x q p p x xx x x x x x ，所以积分⎰+11sin dx x xx qp 仅当11<--p 即2->p 时收敛，且是绝对收敛的，而当2-≤p 时发散．再考虑积分⎰∞++11sin dx x x x qp ，若q p ≥，则1>∀A ，必存在正整数N ，使A N >+42ππ，且当42ππ+≥N x 时，恒有311>+q p x x ．于是对42ππ+='N A ，22ππ+=''N A ，有 62sin 311sin =>+⎰⎰''''''A A A A qp xdx dx x x x ，由Canchy 收敛原理，积分⎰∞++11sin dx x xx qp 发散．若1-<q p ，取0>ε，使1-<+q p ε，即1>--εp q ，由于0sin 1lim sin 1lim =+=++∞→--+∞→εεxxx x x x x xq q x q p p q x ，所以，积分⎰∞++11sin dx x xx qp 绝对收敛．现设q p q <≤-1．先证⎰∞++11sin dx x x x qp 发散．事实上，此时，可取10>A ，使当A x ≥0时，3111>++qp xx ，故有 +∞=≥+=+⎰⎰⎰∞+∞++∞+00sin 31sin 11sin 1A A q p A qp dx x xdx x x xx dx x x x ， 从而⎰∞++11sin dx xx x qp 发散．再证⎰∞++11sin dx x xx qp 收敛．若0=q ，则01<≤-p 此时积分⎰⎰∞+∞+=+11sin 211sin xdx x dx xx x pq p 收敛；若0>q ，由于[]0)1()()1(21<+--='+-q qp q p x x p q p x x x （当x 充分大时），故当x 充分大时，函数qpxx +1单调递减趋于0，而2cos 1cos sin 1≤-=⎰A xdx A有界，故积分⎰∞++11sin dx x xx qp 收敛．于是，得到⎰∞++01sin dx xxx qp 当2->p 且1+>p q 时绝对收敛；当2->p ，1+<<p q p 时条件收敛，其他情况发散．（4）当0≤n 时，积分是发散的当0>n 时，先考虑积分⎰∞++a n dx xx x )1sin( ()1>a ．由于 ⎰⎰∞+∞+-+-=+a n a n dx xx x x x dx xx x )11()1sin()11()1sin(22，。