第4章(2) 多边形填充算法
- 格式:ppt
- 大小:2.02 MB
- 文档页数:12

多边形的平行线填充算法是一种在多边形内部填充平行线的技术。
以下是该算法的基本步骤:
1. 定义一个多边形,可以是一个由一系列点组成的凸多边形,也可以是一个有多个凹边的多边形。
2. 确定填充线的方向和间距。
填充线的方向可以由用户指定,也可以根据多边形的特征自动确定。
填充线的间距则可以根据填充效果的要求进行设置。
3. 计算多边形各点到填充线的距离,将距离小于等于填充线间距的点标记为填充点。
4. 根据填充点的分布情况,将填充点连接成线段,形成填充线。
5. 将填充线与多边形的边界进行交点计算,得到一系列交点。
6. 根据交点的位置关系,将交点连接成线段,形成最终的填充效果。
需要注意的是,对于有多个凹边的多边形,需要进行更复杂的交点计算和线段连接操作,以保证填充效果正确无误。
此外,为了提高填充效率,可以使用一些优化技巧,如排除法、排序算法等。

多边形的偏移填充算法多边形偏移(polygon offset)算法可能我们印象不深,不过用过autoCAD的同学也印象autoCAD 上面也还是有这个功能的。
我们可以用autoCAD上的“正多边形”功能画一个多边形,然后用修改工具中“偏移”按钮,对多边形进行偏移,见图1,从外面的一个大的5边形按照边偏移至里面小的5边形,其中相应边偏移的距离定义为offset值。
图1 AutoCAD中的多边形偏移效果图当然,这只是简单的情况,复杂的情况可能是有多个多边形,其中1个outer多边形,多个inner 多边形,然后offset的时候应该是outer多边形向内offset,inner多边形向外offset。
当一个多边形(特别是凹多边形)初步offset时,可能会发生自交;然后多边形之间也可能会发生相交。
大概思路:这里就需要首先将自交的多边形分裂出来,并选择正确的多边形;然后将选择出来的多边形进行求交计算,再一次将有相交的多边形合并分裂出来,并且选择正确的多边形,这个时候得到的全部多边形就是一次offset出来的结果。
1、为了保证outer多边形能向内offset,inner多边形能向外offset,这里需要保证outer多边形是逆时针方向旋转的,inner多边形是顺时针方向旋转的。
1.1 这里就稍稍讲下多边形的顺逆判断。
在多边形是简单多边形的前提下,其实还是挺简单的,只要找出多边形左下角的一个顶点,然后判断与这个顶点相连的两条边的叉积是否大于0就行了;如果多边形不是简单多边形,比如有自相交,有顶点夹角为0的情况等等,这个时候多边形就不应该有顺逆这种属性吧2、对单个多边形,根据角平分线初步偏移得到角点对于一个角点,可以设这个顶点为curPoint,相连的前一个点为prePoint,下一个点为nexPoint,于是可以得到两个向量a = prePoint – curPoint,b=nexPoint – curPoint。
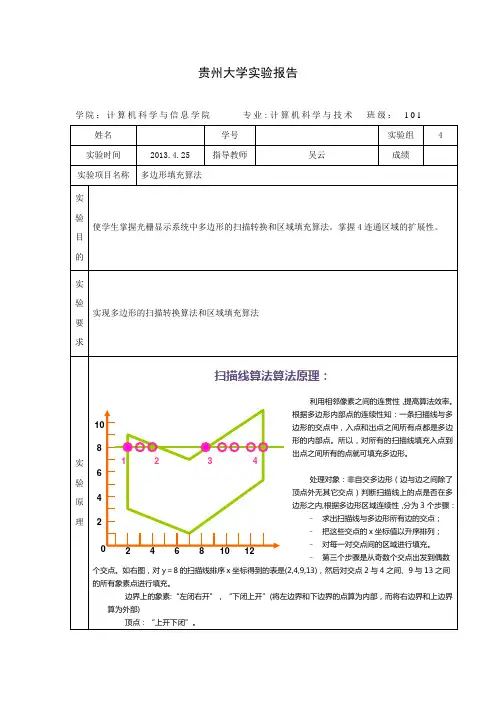

扫描线多边形填充算法扫描线多边形区域填充算法是按照扫描线顺序,计算扫描线与多边形的相交区间,再用要求的颜色显示这些去区间的像素(即完成填充)。
填充过程:1 求交:计算扫面线与多边形个边的交点。
2 排序: 把所有交点按x值地震顺序排序。
2 配对:两两配对,1,和2,3和4 等等。
每对交点代表扫面线与多边形的一个相交区间。
4 填充:把相交区间内的像素设置成多边形颜色。
相交顶点的数目确定:检查相交顶点的两条边的另外两个定点的y值。
按这两个y值中大于交点y值得个数是0,1,2来决定是取0,1或2个。
边界像素取舍:对扫描线与多边形的相交区间取左闭右开。
水平边界处理:水平边不参与求交计算,跳过。
相交:把多边形的所有边放在一个表中,处理每条扫描线是,按顺序从表中取出所有边,分别与扫面线求交。
改进:效率低,可只求与它相交的多边形的边进行求交运算。
算法思想及实现:活性边:与当前扫描线相交的边。
活性边表:把活性边按与扫描线线交点x坐标递增的顺序存放在一个链表中。
活性边的每个节点的内容:X ,X的变化量,Y的最大值,一个指针。
1 存放当前扫描线与边的交点坐标x值。
2 存放从当前扫描线到下一条扫描线间x的增量3 存放该边所交的最高扫面线号ymax;4 存放指向下一条边的指针。
算法的主要步骤:建立NET(new edge list)从最低扫面线开始到最高扫面线循环。
建立或调整AET(active edge list)按照AET总的接点顺序填充。
算法描述:算法描述:void polyfill (多边形polygon, 颜色color){for (各条扫描线i ){ 初始化新边表头指针NET [i];把ymin = i 的边放进边表NET [i];}y = 最低扫描线号;初始化活性边表AET为空;for (各条扫描线i ){ 把新边表NET[i]中的边结点用插入排序法插入AET表,使之按x坐标递增顺序排列;遍历AET表,把配对交点区间(左闭右开)上的象素(x,y),用drawpixel (x, y, color) 改写象素颜色值;遍历AET表,把y max= i +1的结点从AET表中删除,并把y max > i+1结点的x值递增D x;若允许多边形的边自相交,则用冒泡排序法对AET表重新排序;}} /* polyfill */。


试验实验一:图形的区域填充一、实验目的区域填充是指先将区域内的一点(常称为种子点)赋予给定颜色,然后将这种颜色扩展到整个区域内的过程。
区域填充技术广泛应用于交互式图形、动画和美术画的计算机辅助制作中。
本实验采用递归填充算法或打描线算法实现对光栅图形的区域填充。
通过本实验,可以掌握光栅图形编程的基本原理和方法。
实验内容掌握光栅图形的表示方法,实现种子算法或扫描线算法。
通过程序设计实现上述算法。
建议采用VC++实现OpenGL程序设计。
三、实验原理、方法和手段递归算法在要填充的区域内取一点(X, Y)的当前颜色记为oldcoloo用要填充的颜色ne wcolor去取代,递归函数如下:procedure flood-fill(XXoldcoloLnewcolor:integer); beginif getpixel(fiainebufier,x,y)=oldcolorthen beginsetpixel(fiamebuffer,x,y,newcolor); flood-fill(X.Y+1 .oldcoloLiiewcolor);flood-fill(X.Y^ 1 ,oldcoloi;newcolor); flood-fill(X-l,Y;oldcoloi;newcolor); flood-fill(X+l,Yoldcoloi;newcolor);endend扫描线算法扫描线算法的效率明显高于递归算法,其算法的基本思想如下:(1)(初始化)将算法设置的堆栈置为空,将给定的种子点(x,y)压入堆栈。
(2)(出栈)如果堆栈为空,算法结束;否则取栈顶元素(x,y)作为种子点。
(3)(区段填充)从种子点(x,y)开始沿纵坐标为y的当前扫描线向左右两个方向逐个象素进行填色,其值置为newcoloi;直到抵达边界为止。
(4)(定范围)以XleA和Xn血分别表示在步骤3中填充的区段两端点的横坐标。
(5)(进栈)分别在与当前扫描线相邻的上下两条打描线上,确定位于区间[Xldb Xn 曲]内的给定区域的区段。


多边形填充算法
多边形填充算法是一种计算机图形学中的算法,用于将一个封闭的多边形区域(如矩形、三角形、梯形等)填充成指定的颜色。
在计算机图形学中,多边形是由一系列线段(边)连接成的封闭区域。
填充算法的目的是在多边形的内部填充指定的颜色。
这种算法通常用于计算机辅助设计、计算机游戏开发、计算机动画、计算机视觉等领域。
填充算法有多种实现方法,包括扫描线填充、种子填充、边界填充、区域分割等。
其中,扫描线填充是最常见的一种算法,它的基本思想是从多边形的最上面一行开始,逐行向下扫描,同时记录扫描线和多边形之间的交点。
当扫描线与多边形的边相交时,根据交点的奇偶性来判断该点是否在多边形内部。
如果是奇数个交点,则该点在多边形内部,需要进行填充;如果是偶数个交点,则该点在多边形外部,不需要填充。
种子填充是另一种常见的填充算法,它的基本思想是从多边形内部的一个点(种子)开始,向外扩散填充。
在扩散过程中,同时记录已经填充过的像素点,避免重复填充。
这种算法的优点是填充速度较快,但容易出现填充区域不封闭、填充效果不理想等问题。
边界填充和区域分割是另外两种填充算法,它们的实现方式比较复杂,但可以处
理比较复杂的填充情况,例如多个子多边形共同填充、奇异多边形填充等。
总的来说,多边形填充算法在计算机图形学中具有重要的应用价值和研究意义,不同的填充算法各有优缺点,需要根据具体的需求和应用场景来选择合适的算法。

多边形填充算法本在计算机图形学中,使用多边形填充算法可以实现各种图形的绘制,例如:圆形、椭圆形、字母等。
对于任意形状的多边形来说,其内部像素点的坐标是无法直接计算得到的,因此需要通过一定的算法来实现。
常见的多边形填充算法有扫描线填充算法和边界填充算法。
接下来我们来详细了解这两种算法。
扫描线填充算法是通过扫描多边形上的每一条水平线,找到与多边形相交的线段,并进行填充操作。
具体步骤如下:1.找到多边形的最高点和最低点,作为扫描线的起点和终点。
2.将扫描线从起点依次向下移动,直到到达终点。
3.在每一条扫描线上,找到与多边形相交的线段。
4.根据线段的起点和终点,计算交点的x坐标,并从起点到终点对应的像素点进行填充。
5.重复步骤4,直到所有的扫描线都处理完毕。
扫描线填充算法的优点是简单易懂,适用于一般情况。
但是对于复杂的多边形来说,会存在边界交叉的情况,需要特殊处理。
边界填充算法是通过检测多边形的边界点,并进行填充操作。
具体步骤如下:1.找到多边形的最左边、最右边、最上边和最下边的点,作为边界点。
2.从最上边的点开始,依次向下遍历每一行像素点。
3.在每一行中,寻找与多边形边界相交的点,并进行填充操作。
4.重复步骤3,直到到达最下边的点。
边界填充算法的优点是对具有复杂交叉边界的多边形也能进行正确的填充操作。
但是对于非凸多边形来说,边界填充算法可能会有空隙出现。
除了以上两种常见的多边形填充算法,还有其他一些算法也可以实现多边形的填充操作,例如:扫描转换填充算法、边界边框填充算法等。
在实际应用中,多边形填充算法通常结合图形处理库或者计算机图形学软件来实现。
这些软件提供了丰富的函数和方法,可以直接调用进行多边形的填充操作。
综上所述,多边形填充算法是计算机图形学中的一个重要算法。
通过扫描线填充算法或者边界填充算法,可以实现对任意形状多边形的填充操作。
随着计算机图形学的发展,多边形填充算法也不断进化和优化,以满足不同应用场景的需求。

多边形填充算法-有序边表法(扫描线算法)1.算法的基本思想(扫描线连贯性原理): 对于⼀个给定的多边形,⽤⼀组⽔平(垂直)的扫描线进⾏扫描,对每⼀条扫描线均可求出与多边形边的交点,这些交点将扫描线分割成落在多边形内部的线段和落在多边形外部的线段;并且⼆者相间排列。
于是,将落在多边形内部的线段上的所有象素点赋以给定的⾊彩值。
算法中不需要检验每⼀个象素点,⽽只考虑与多边形边相交的交点分割后的扫描线段。
2.算法求解:对于每⼀条扫描线的处理:1)求交点:⾸先求出扫描线与多边形各边的交点;2)交点排序:将这些交点按X坐标递增顺序排序;3)交点匹配:即从左到右确定落在多边形内部的那些线段;4)区间填充:填充落在多边形内部的线段。
3.求交点的⽅法最简单的办法:将多边形的所有边放在⼀个表中,在处理每条扫描线时,从表中顺序取出所有的边,分别求这些边与扫描线的交点。
不使⽤该⽅法的原因:将做⼀些⽆益的求交点动作,因为扫描线并不⼀定与多边形的边相交,扫描线只与部分甚⾄较少的边相交;因此,在进⾏扫描线与多边形边求交点时,应只求那些与扫描线相交的边的交点。
确定与扫描线相交的边:⽤边表来确定哪些边是下⼀条扫描线求交计算时应该加⼊运算的。
4.边表(ET):ET的意义在于为扫描线提供待加⼊的新边信息。
建⽴边的分类表ET(Edge Table),每个结点结构如下:(Ymax ,ΔX ,X Ymin,)Ymax:边的最⼤Y值;ΔX:从当前扫描线到下⼀条扫描线之间的X增量(dX/ dY);X Ymin:边的下端点的X坐标;next:指针,指向下⼀条边。
边的分类表可以这样建⽴:先按下端点的纵坐标(y值)对所有边作桶分类,再将同⼀组中的边按下端点X坐标递增的顺序进⾏排序, X坐标还相同的按ΔX递增的顺序进⾏排序。
5.活性边表AET把与当前扫描线相交的边称活化边AEL(Active Edge List) 。
组成的表称为活性表AET,其数据域组成如下:Ymax :存放边的上端点Y坐标;X :边与当前扫描线交点的X坐标;ΔX ,next指针:同边表。

算法系列之十二:多边形区域填充算法--递归种子填充算法平面区域填充算法是计算机图形学领域的一个很重要的算法,区域填充即给出一个区域的边界(也可以是没有边界,只是给出指定颜色),要求将边界范围内的所有象素单元都修改成指定的颜色(也可能是图案填充)。
区域填充中最常用的是多边形填色,本文中我们就讨论几种多边形区域填充算法。
一、种子填充算法(Seed Filling)如果要填充的区域是以图像元数据方式给出的,通常使用种子填充算法(Seed Filling)进行区域填充。
种子填充算法需要给出图像数据的区域,以及区域内的一个点,这种算法比较适合人机交互方式进行的图像填充操作,不适合计算机自动处理和判断填色。
根据对图像区域边界定义方式以及对点的颜色修改方式,种子填充又可细分为几类,比如注入填充算法(Flood Fill Algorithm)、边界填充算法(Boundary Fill Algorithm)以及为减少递归和压栈次数而改进的扫描线种子填充算法等等。
所有种子填充算法的核心其实就是一个递归算法,都是从指定的种子点开始,向各个方向上搜索,逐个像素进行处理,直到遇到边界,各种种子填充算法只是在处理颜色和边界的方式上有所不同。
在开始介绍种子填充算法之前,首先也介绍两个概念,就是“4-联通算法”和“8-联通算法”。
既然是搜索就涉及到搜索的方向问题,从区域内任意一点出发,如果只是通过上、下、左、右四个方向搜索到达区域内的任意像素,则用这种方法填充的区域就称为四连通域,这种填充方法就称为“4-联通算法”。
如果从区域内任意一点出发,通过上、下、左、右、左上、左下、右上和右下全部八个方向到达区域内的任意像素,则这种方法填充的区域就称为八连通域,这种填充方法就称为“8-联通算法”。
如图1(a)所示,假设中心的蓝色点是当前处理的点,如果是“4-联通算法”,则只搜索处理周围蓝色标识的四个点,如果是“8-联通算法”则除了处理上、下、左、右四个蓝色标识的点,还搜索处理四个红色标识的点。
计算机图形学多边形填充算法计算机图形学中的多边形填充算法是指将给定的多边形区域进行颜色填充,以使其完全填充的过程。
在图形学中,多边形是由一系列连续的线段组成的封闭图形。
填充算法可用于渲染图形、绘制图像等应用场景。
多边形填充算法的目标是根据设计要求和用户输入,给定一个多边形的边界,将多边形的内部区域进行颜色填充。
填充算法的实现涉及到图像的扫描线和区域判定,以确定填充的区域和颜色。
在本文中,我们将介绍常见的多边形填充算法,包括扫描线填充算法、边界填充算法等,并讨论它们的优缺点和适用场景。
扫描线填充算法扫描线填充算法是一种常见且简单的多边形填充算法。
该算法将多边形划分为一条条水平扫描线,并通过判断扫描线与多边形边界的交点,确定填充区域。
具体步骤如下:1.找到多边形边界的最上端和最下端。
2.从最上端开始,逐行进行扫描。
3.在每一行,通过求解扫描线与多边形边界的交点,确定填充区域。
4.对于每个填充区域,根据设计要求进行颜色填充。
扫描线填充算法的优点是简单易懂、实现较为容易。
然而,该算法存在一些缺点。
首先,对于具有复杂形状的多边形,扫描线填充算法可能会产生很多不必要的计算,导致效率降低。
其次,该算法需要处理多边形边界相交的情况,可能出现像素重复填充的问题,需要进行额外的处理。
边界填充算法边界填充算法是另一种常见的多边形填充算法。
与扫描线填充算法不同的是,边界填充算法是从多边形的边界出发,向内部填充颜色。
该算法的基本思想是对多边形的每条边进行填充,最终得到多边形的填充区域。
具体步骤如下:1.遍历多边形的每条边,保存每条边的起点和终点。
2.对于每个边,根据设计要求进行颜色填充。
3.对于多边形内部的区域,根据边界的颜色填充。
边界填充算法的优点是适用于复杂形状的多边形,无需处理边界相交的问题。
然而,该算法的实现相对复杂,需要处理边界的细化以及边缘像素重复填充的问题。
适用场景不同的多边形填充算法在不同场景下有不同的适用性。
多边形的填充——扫描线算法(原理)2007年10月05日星期五 11:52多边形在计算机中有两种表示:点阵表示和顶点表示。
顶点表示是用多边形的顶点的序列来描述多边形,该表示几何意义强、占内存少,但它不能直观地说明哪些像素在多边形内。
点阵表示是用位于多边形内的象素的集合来刻划多边形,该方法虽然没有多边形的几何信息,但具有面着色所需要的图像表示形式。
多边形填充就是把多边形的顶点表示转换为点阵表示,即从多边形的给定边界出发,求出位于其内部的各个像素,并将帧缓冲器内的各个对应元素设置为相应的灰度或颜色。
多边形填充最常用的方法就是扫描线算法。
下面分两篇文章介绍这种算法的原理和具体实现。
这里所介绍的算法只是针对非自交多边形,这些多边形可以是凸的、凹的或者带有空洞的。
所谓扫描线算法就是找到多边形的最小y值和最大y值,然后用这个范围内的每一条水平线与多边形相交,求得交点,再绘制线段。
所以我们只需要对一条水平线进行分析就可以。
很显然,一条扫描线和多边形有偶数个交点,将这些交点按照x值从小到大排列,然后取第1、2个绘制,第3、4个绘制......直到所有交点都被取完。
所以,对于一条扫描线,我们需要做的工作可以分为三个步骤:1)求出扫描线与多边形边的交点 2)将交点按照x升序排列 3)将排好序的交点两两配对,然后绘制相应线段。
这三个步骤中,后两个步骤很简单,没有特别的内容需要介绍。
但是第一个步骤比较麻烦。
这里有几个问题需要解决。
一是当扫描线与顶点相交时,交点的取舍。
当与那个顶点关联的边在扫描线同侧时,交点自然算两次,当与那个顶点关联的边在扫描线两侧时,交点只能算一次。
我们使用“下闭上开”的办法。
二是多边形边界上的像素取舍,我们采用“左闭右开”的办法。
三是如何减少计算量。
在绘制直线时,有一种DDA算法,它是利用(x,y)直接求出下一个点位于(x+1,y+m)或者(x+1/m, y+1)。
在这里可以利用这一点。
当已经得到y = e和多边形所有边的交点时,对于下一条扫描线y=e+1,如果没有新边与y=e+1相交,就可以推出y = e+1 和多边形所有边的交点。
任意多边形区域的快速填充算法一、前言任意多边形区域的快速填充算法是计算机图形学中的一个重要问题,其应用广泛,例如在计算机游戏、数字地图等领域中都有广泛的应用。
本文将介绍几种常见的任意多边形区域的快速填充算法,包括扫描线算法、边界填充算法、种子填充算法等。
二、扫描线算法扫描线算法是一种基于扫描线原理的填充算法,其基本思想是将区域划分为若干个水平方向上的扫描线,然后在每条扫描线上找到交点,并根据交点进行填充。
具体步骤如下:1. 将多边形顶点按照纵坐标从小到大排序;2. 从最小纵坐标开始,依次向上扫描每条水平方向上的线段;3. 对于每条水平方向上的线段,找到与之相交的多边形边界,并记录下所有交点;4. 根据相邻两个交点之间是否为奇数个来确定是否需要进行填充。
三、边界填充算法边界填充算法也是一种常见的任意多边形区域的快速填充算法,其基本思想是通过递归调用来进行填充。
具体步骤如下:1. 对于每个多边形边界上的像素点,将其标记为“边界点”;2. 从任意一个未填充的内部像素点开始,向四周搜索,如果遇到“边界点”则停止搜索,并将搜索路径上的所有像素点标记为已填充;3. 重复步骤2直到所有内部像素点都被填充。
四、种子填充算法种子填充算法也是一种常见的任意多边形区域的快速填充算法,其基本思想是通过找到一个内部像素点作为“种子”,然后向四周扩散进行填充。
具体步骤如下:1. 随机选择一个内部像素点作为“种子”,并将其标记为已填充;2. 向四周搜索,如果遇到未被标记为已填充的像素,则将其标记为已填充,并加入到待处理列表中;3. 重复步骤2直到待处理列表为空。
五、总结以上介绍了几种常见的任意多边形区域的快速填充算法,每种算法都有其特定的优缺点,选择合适的算法需要根据具体的应用场景进行考虑。
在实际应用中,还需要考虑算法的效率、稳定性、可扩展性等方面的问题。
多边形填充算法算法原理:确定多边形所占有的最大扫描线数,得到多边形顶点的最小和最大y值(ymin和ymax);从y=ymin到y=ymax,每次用一条扫描线进行填充。
对一条扫描线填充的过程可分为四个步骤:a.求交b.排序c.交点配对d.区间填色。
功能操作步骤:先在面板上绘制一个多边形;选中;按下实现该算法的工具;弹出保存对话框;输入文件名,确定之后,保存成bmp 位图文件。
功能实现流程:1.添加工具:在工具栏上添加一个类型为button的工具;然后在属性框设置text为多边形填充;设置name为rasterpolygon;设置Image 为前面提供位置的任意图片或自己绘制一个图片。
设置事件框中的单击事件click;对着click双击,弹出代码文件。
2.为事件函数添加如下代码//c_state = GUIState.RasterPolygon;//panel1.Cursor = Cursors.Cross;Point_T opt = new Point_T(0, 0);double pixelsize = 5;int rs = (int)(panel1.Size.Height / pixelsize);int cs = (int)(panel1.Size.Width / pixelsize);Raster_T mapras = new Raster_T(rs, cs, pixelsize, opt);////构造地图栅格//List<PixelPosition_T> mappixel = RasterationMap(choosegeos, mapras);///栅格化地图//cp = new Point(i_e.X, i_e.Y);//PixelPosition_T cpp = RasterationPoint(new Point_T(cp.X, cp.Y), mapras);List<PixelPosition_T> pypixel = RasterationPolygon(choosegeos, mapras);//多边形区域填充////导出成位图Bitmap bmp = new Bitmap(mapras.Cols + 1, mapras.Rows + 1);foreach (PixelPosition_T pp in pypixel){bmp.SetPixel(pp.Col, pp.Row, Color.Red);}SaveFileDialog sfd = new SaveFileDialog();//使用保存对话框sfd.ShowDialog();//string bmppath = "c:" + "\\" + "mybmp" + ".bmp";string bmppath = sfd.FileName;bmp.Save(bmppath);////导出位图3.添加多边形填充算法代码1)x轴扫描转换算法public List<PixelPosition_T> RasterationPolygon(Map_T map, Raster_T ras){List<PixelPosition_T> pypixel=new List<PixelPosition_T>();foreach (Geometry_T geo in map.Geofeatures){if (geo.GetType() == typeof(Ring_T)){Ring_T ri = (Ring_T)geo;List<Point_T> pypts = new List<Point_T>();foreach (Line_T li in ri.Path){pypts.Add(li.Frompt);}CompareY comy=new CompareY();CompareX comx = new CompareX();pypts.Sort(comy);//计算最大最小y值,并将此两点栅格化PixelPosition_T ppmax = RasterationPoint(pypts[pypts.Count - 1], ras);PixelPosition_T ppmin = RasterationPoint(pypts[0], ras);//pypixel.Add(ppmax);//pypixel.Add(ppmin);for (int i = 0; i <=(ppmax.Row - ppmin.Row); i++)//?//循环遍历,使用递进一个单位栅格中心线{double y = (ppmin.Row + i + 0.5) * ras.Pixelsize + ras.Originpt.Y;Point_T pt1 = new Point_T(ras.Originpt.X,y);Point_T pt2=new Point_T(ras.Originpt.X+ras.Cols*ras.Pixelsize,y);Line_T cline = new Line_T(pt1,pt2);List<Point_T> interpts = new List<Point_T>();//依次和多边形的边求交点foreach (Line_T li in ri.Path){if (cline.Frompt.Y < Math.Max(li.Frompt.Y, li.Topt.Y) &&cline.Frompt.Y > Math.Min(li.Frompt.Y, li.Topt.Y)){Point_T interpt = IntersectPoint(cline, li);//求交点interpts.Add(interpt);}}interpts.Sort(comx);//对交点按照x值排序for (int j = 0; j < interpts.Count - 1; j = j + 2)//交点两两配对成水平直线{Line_T pline = new Line_T(interpts[j], interpts[j + 1]);List<PixelPosition_T> cpixel=RasterationHonLine(pline, ras);//栅格化水平直线pypixel.AddRange(cpixel);}}}}return pypixel;}2)两个排序类(分别以x值和以y值对点排序)public class CompareX:IComparer<Point_T>{public int Compare(Point_T pt1, Point_T pt2){return pareTo(pt2.X);// Compare(pt1.X, pt2.X);}}public class CompareY : IComparer<Point_T>{public int Compare(Point_T pt1, Point_T pt2){return pareTo(pt2.Y);// Compare(pt1.Y, pt2.Y);}}3)栅格化水平线段public List<PixelPosition_T> RasterationHonLine(Line_T line, Raster_T ras) {List<PixelPosition_T> pixels = new List<PixelPosition_T>();PixelPosition_T ppmax = RasterationPoint(line.Topt, ras);PixelPosition_T ppmin = RasterationPoint(line.Frompt, ras);pixels.Add(ppmin);for (int i = 1; i < (ppmax.Col - ppmin.Col); i++){PixelPosition_T cpp = new PixelPosition_T(ppmin.Row, ppmin.Col + i); pixels.Add(cpp);}pixels.Add(ppmax);return pixels;}以上步骤成功完成后将能运行出以下结果:。