图形学实验报告四 多边形填充算法

学生实验报告
实验课名称：计算机图形学
实验项目名称：多边形填充算法
专业名称：计算机科学与技术
班级：
学号：
学生姓名：
教师姓名：
2016年4月30 日
六．运行结果与分析：
图1：扫描线种子填充算法
图2：种子填充算法
七．实验中遇到的问题、解决方法及体会：
多边形的填充对我来说很困难，因为一开始我不知道要输入什么数据，后来我决定要输入五个点来形成一个五边形，但是输入的顺序是一个大问题。

后来我采取顺序输入的方法，但是程序运行时常常崩溃，结果不尽人意。

最后，我在同班同学的帮助之下，找到了自己的问题，完成了填充。

多边形的平行线填充算法是一种在多边形内部填充平行线的技术。

以下是该算法的基本步骤：
1. 定义一个多边形，可以是一个由一系列点组成的凸多边形，也可以是一个有多个凹边的多边形。

2. 确定填充线的方向和间距。

填充线的方向可以由用户指定，也可以根据多边形的特征自动确定。

填充线的间距则可以根据填充效果的要求进行设置。

3. 计算多边形各点到填充线的距离，将距离小于等于填充线间距的点标记为填充点。

4. 根据填充点的分布情况，将填充点连接成线段，形成填充线。

5. 将填充线与多边形的边界进行交点计算，得到一系列交点。

6. 根据交点的位置关系，将交点连接成线段，形成最终的填充效果。

需要注意的是，对于有多个凹边的多边形，需要进行更复杂的交点计算和线段连接操作，以保证填充效果正确无误。

此外，为了提高填充效率，可以使用一些优化技巧，如排除法、排序算法等。

试验实验一:图形的区域填充一、实验目的区域填充是指先将区域内的一点（常称为种子点）赋予给定颜色，然后将这种颜色扩展到整个区域内的过程。

区域填充技术广泛应用于交互式图形、动画和美术画的计算机辅助制作中。

本实验采用递归填充算法或打描线算法实现对光栅图形的区域填充。

通过本实验，可以掌握光栅图形编程的基本原理和方法。

实验内容掌握光栅图形的表示方法，实现种子算法或扫描线算法。

通过程序设计实现上述算法。

建议采用VC++实现OpenGL程序设计。

三、实验原理、方法和手段递归算法在要填充的区域内取一点（X, Y）的当前颜色记为oldcoloo用要填充的颜色ne wcolor去取代，递归函数如下：procedure flood-fill（XXoldcoloLnewcolor:integer）; beginif getpixel（fiainebufier,x,y）=oldcolorthen beginsetpixel（fiamebuffer,x,y,newcolor）; flood-fill（X.Y+1 .oldcoloLiiewcolor）;flood-fill（X.Y^ 1 ,oldcoloi;newcolor）; flood-fill（X-l,Y；oldcoloi;newcolor）; flood-fill（X+l,Yoldcoloi;newcolor）;endend扫描线算法扫描线算法的效率明显高于递归算法，其算法的基本思想如下：（1）（初始化）将算法设置的堆栈置为空，将给定的种子点（x,y）压入堆栈。

（2）（出栈）如果堆栈为空，算法结束；否则取栈顶元素（x,y）作为种子点。

（3）（区段填充）从种子点（x,y）开始沿纵坐标为y的当前扫描线向左右两个方向逐个象素进行填色，其值置为newcoloi;直到抵达边界为止。

（4）（定范围）以XleA和Xn血分别表示在步骤3中填充的区段两端点的横坐标。

（5）（进栈）分别在与当前扫描线相邻的上下两条打描线上，确定位于区间［Xldb Xn 曲］内的给定区域的区段。

实验二2-2一、实验题目给定四个点绘制图4-44所示的不同转角的两个正方形，使用有效边表算法进行填充，填充效果如图4-45所示，注意采用“左闭右开”和“上闭下开”的原则，使得每个正方形的右边界和下边界没有填充。

二、实验思想有效边表填充算法通过维护边表和有效边表，避开了扫描线与多边形所有边求交的复杂运算。

填充原理是按照扫描线从小到大的移动顺序，计算当前扫描线与有效边的交点，然后把这些交点按x值递增的顺序进行排序、配对，以确定填充区间，最后用指定颜色填充区间内的所有像素，即完成填充工作。

三、实验代码void CTestView::GetMaxX()//获得屏幕宽度{CRect Rect;GetClientRect(&Rect);MaxX=Rect.right;}void CTestView::GetMaxY()//获得屏幕高度{CRect Rect;GetClientRect(&Rect);MaxY=Rect.bottom;}void CTestView::ReadPoint()//读入点表函数{//设置第一个正方形的4个顶点int a=160;P1[0]=CP2(MaxX/4-a,MaxY/2+a);//P0P1[1]=CP2(MaxX/4+a,MaxY/2+a);//P1P1[2]=CP2(MaxX/4+a,MaxY/2-a);//P2P1[3]=CP2(MaxX/4-a,MaxY/2-a);//P3//设置第二个正方形的4个顶点int b=ROUND(sqrt(2)*a);P2[0]=CP2(3*MaxX/4,MaxY/2+b);//P0P2[1]=CP2(3*MaxX/4+b,MaxY/2);//P1P2[2]=CP2(3*MaxX/4,MaxY/2-b);//P2P2[3]=CP2(3*MaxX/4-b,MaxY/2);//P3}void CTestView::DrawRect(CDC *pDC,CP2 *P)//绘制正方形函数{CP2 T;CLine line;for(int i=0;i<4;i++)//边循环{if(i==0){line.MoveTo(pDC,P[i]);T=P[0];}else{line.LineTo(pDC,P[i]);;}}line.LineTo(pDC,T);//闭合}void CTestView::OnMENUIFill(){// TODO: Add your command handler code hereCOLORREF FColor;CColorDialog ccd(RGB(255,0,0));if(ccd.DoModal()==IDOK)//调用调色板选取色{FColor=ccd.GetColor();m_Red=GetRValue(FColor);//获得颜色的红色分量m_Green=GetGValue(FColor);//获得颜色的绿色分量m_Blue=GetBValue(FColor);//获得颜色的蓝色分量}RedrawWindow();//刷新屏幕FillRect(P1);//填充正方形1FillRect(P2);//填充正方形2}void CTestView::FillRect(CP2 *P)//填充正方形函数{CFill fill;CPi2 Point[4];for(int i=0;i<4;i++){Point[i].x=P[i].x;Point[i].y=ROUND(P[i].y);Point[i].c=CRGB(double(m_Red)/255.0,double(m_Green)/255.0,double(m_Blue)/255.0);}CDC *pDC=GetDC();fill.SetPoint(Point,4);//填充正方形fill.CreateBucket();fill.CreateEdge();fill.Gouraud(pDC);ReleaseDC(pDC);}四、实验截图。

计算机图形学四连通区域种子填充算法实验————————————————————————————————作者: ————————————————————————————————日期:ﻩ《计算机图形学实验》报告任课教师:钱文华2０16年春季学期实验:四连通区域种子填充算法实验时间：201６年12月8日实验地点：信息学院22０4实验目的：掌握种子填充算法的原理，并会用种子填充算法和opｅｎｇl并结合使用ｃ+＋语言编写程序绘制多边形。

实验原理:种子填充算法又称为边界填充算法。

其基本思想是:从多边形区域的一个内点开始，由内向外用给定的颜色画点直到边界为止。

如果边界是以一种颜色指定的,则种子填充算法可逐个像素地处理直到遇到边界颜色为止。

内点的检测条件：ｉf(iｎｔerｉoｒCｏloｒ!=bo ｒｄerCoｌor&&interｉorColoｒ!＝ｆiｌlCｏlｏr）。

种子填充算法常用四连通域和八连通域技术进行填充操作。

从区域内任意一点出发，通过上、下、左、右四个方向到达区域内的任意像素。

用这种方法填充的区域就称为四连通域;这种填充方法称为四向连通算法。

从区域内任意一点出发,通过上、下、左、右、左上、左下、右上和右下八个方向到达区域内的任意像素。

用这种方法填充的区域就称为八连通域；这种填充方法称为八向连通算法。

一般来说，八向连通算法可以填充四向连通区域,而四向连通算法有时不能填充八向连通区域。

四向连通填充算法:a）种子像素压入栈中;b)如果栈为空,则转e）；否则转c）;c) 弹出一个像素,并将该像素置成填充色;并判断该像素相邻的四连通像素是否为边界色或已经置成多边形的填充色，若不是,则将该像素压入栈;d)转b）;ｅ）结束。

四连通填充算法利用到了递归的思想。

本实验只包括四连通填充算法程序代码:#ｉncludｅ<ｇlut.h>＃ｉｎｃlｕde<ｓtdｌib．h>＃ｉncｌudｅ<math．h>#include<ｗindowｓ.h＞voidｉniｔ（vｏid）{ glCｌearColor(１．０，１.0,1．0,0.０）；glMatrixMoｄｅ（ＧL_PROJＥCTION）;gｌｕOrtho２D（０．0，30０．0，０.0,30０.0);}voｉd setPixel(inｔx，ｉnｔy,lｏｎｇｆillCoｌor）{ ｇlColor3f（fｉllCoｌoｒ<<16,filｌCoｌor<<８,fillCｏloｒ)；ｇlＢｅgin（ＧL_ＰＯINTＳ);ｇlＶｅｒteｘ2i（x,y）;ｇlEnｄ();}ｖｏｉｄboundaryFill４(iｎt x,ｉnｔy,lｏng fillＣolor,lｏng bordeｒColor）{ unｓｉgneｄchａr paｒams[3];loｎg interioｒCoｌoｒ;glRｅaｄPixels(ｘ，y,1,1,GL_RGB,GＬ＿UNSIＧNＥD_BYＴE,par ａms）;interiorCoｌoｒ=RGB(paraｍs[0],ｐarａms[１］,paｒaｍs[2])；ｉf(inteｒiorＣolor!=boｒderCｏloｒ＆＆inteｒiｏrCoｌｏr!=filｌColor){ setＰixeｌ(x，ｙ,fｉｌlCoｌｏr);ｂoundaryFill4（x＋1,y,filｌＣoｌｏr,ｂordeｒCｏlor);ｂｏunｄaｒyＦｉｌl4(ｘ-1，y，fiｌlＣolor,borderColor); boundaryFilｌ４(x,ｙ+1,ｆｉlｌColｏr,borｄeｒCoｌor)；ｂounｄarｙFill4(x，y-1，ｆｉllColｏr，ｂorｄerＣolor);} }voiｄlineＳegment(voｉd) {long bｏrｄerCｏｌoｒ=RGB（255，0,０);lｏngｆiｌlColoｒ=RGB（０，0，255）;glClｅar（ＧL_COＬOR＿BUFFER_BIT); glCｏloｒ３ｆ(２55，0,0); ｇlＢegｉn（GL_ＬINE＿ＬＯＯP);glVeｒtex2ｉ(0,４0);glVｅｒteｘ2i(2０,0);glＶertex２i(６0,0）；glＶeｒtｅx2ｉ(80，4０）;ｇlVｅｒtex2i(６0,80);gｌVertex２i(20,80);gｌＥnd();boundaryＦill4(６０,60，ｆｉllＣolor,ｂorderColｏr)；gｌFlush()；}voｉｄmain(ｉｎt argc,chａr＊*aｒgv）｛ｇlutIｎｉｔ(&ａr ｇc,aｒｇv);glｕtInitDｉsｐｌaｙMode(GLUＴ＿ＳＩNGLE｜GLUT_ＲGB); glutInitＷindowPｏsiｔion（1５0,10０）;gluｔIｎitWinｄoｗSizｅ(300,３0０）;glutＣreateＷｉｎdow（"种子填充"）；init();glutDisｐlayFｕｎｃ(lｉneＳegｍeｎt);gｌｕtMａinＬｏoｐ(）;}上实验课时机房的实验结果:后来的实验结果:glVｅrteｘ2i（0,40);gｌＶerteｘ２i（20，0);glVerｔex2i（60,０);glVerteｘ2i（８0，４０);gｌＶertｅx2ｉ(60，80);ｇlＶerteｘ2i(２0,80)；ｇlEnｄ();ｂｏｕndaryFｉlｌ4(60,60，ｆｉlｌCｏlor,ｂorderＣoｌor）；以上这段程序改成如下glVerｔex2ｉ(９0，40);glVｅrtｅx２i（１2０, １00）;ｇlVertex2i(90,1６0);glVertｅｘ２i(60, 160);ｇlVertex2i(60, ４０);glEnd()；bouｎｄaryFilｌ4(７0,6０,fiｌｌCｏｌoｒ,bｏｒderCoｌor); 改变参数后：再把ｇlVeｒｔｅx2i（9０，40);glVertｅｘ２i(120, 100）；glＶｅrｔex2i(90,160）;glＶerｔex2i(60, １6０）;glVｅrtex２i（６0, 40）;gｌＥnd（);bｏundaryFill4（70,6０,fiｌlCｏloｒ,boｒdｅrCｏlor）；改成glVeｒtex2i(100, １０0)；glVｅrteｘ2i(２00, 100);gｌVｅｒteｘ2ｉ(1５0,150);/／glVｅrteｘ2ｉ(60, 1６0);／/glVertｅx2i(6０, 40)；glＥnd();ｂoundaryFill4(150，1２0,fiｌlCｏlor，borｄerCoｌoｒ);后的结果如下图:实验总结:通过多组数据的测试，知道了上面算法的正确,普适性。

实验四区域填充算法的实现班级 08信计2班学号 20080502082 姓名分数一、实验目的和要求：1、理解区域的表示和类型。

2、能正确区分四连通和八连通的区域3、了解区域填充的实验原理。

4、利用C++实现区域填充的递归算法。

二、实验内容：1假设在多边形内有一像素已知，由此出发利用连通性找到区域内所有像素。

2 取（x，y）为种子点将整个区域填充为新的颜色。

3 进行递归填充。

三、实验结果分析区域填充属性包括填充样式，填充颜色和填充图案的类型。

C语言中定义了某种图形后，即可调用-floodfill函数，对指定区域进行填充. 程序代码#define pi 3.141592#define MAX(a,b) (a>b)? a:b#define MIN(a,b) (a<b)? a:b#include "graphics.h"#include "math.h"struct edge {int ymax;float x;float delat;struct edge * pedge; };struct point{int x;int y;} ;struct et { struct edge * pedge;int n;};struct edge g_aet[10];struct edge dge[10];struct et g_et[10];struct point point1,point2;int ZUO(float x){ if((int)x==x)return (int)x;return (int)x+1;}int YOU(float x){ if((int)x==x)return (int)x-1;return (int)x;}int k=400,l=0;void draw1(){int i,t,j,a,c,p,z; float b;struct edge temp;for(i=k;i<=l;i++){a=0;for(t=0;t<=9;t++){ if(g_et[t].n==i) break;}for(j=0;j<=9;j++){ if(g_aet[j].ymax==0) break;}if(t!=10){ g_aet[j].ymax=g_et[t].pedge->ymax;g_aet[j].x=g_et[t].pedge->x;g_aet[j].delat=g_et[t].pedge->delat;if(g_et[t].pedge->pedge!=0){g_aet[j+1].ymax=g_et[t].pedge->pedge->ymax;g_aet[j+1].x=g_et[t].pedge->pedge->x;g_aet[j+1].delat=g_et[t].pedge->pedge->delat; }}for(j=0;j<=9;j++){ if(g_aet[j].ymax==0) break; }j--;for(t=0;t<=j;t++){ for(z=0;z<=j-1;z++){if(g_aet[z].x>g_aet[z+1].x){ temp.ymax=g_aet[z].ymax;temp.x=g_aet[z].x;temp.delat=g_aet[z].delat;g_aet[z].ymax=g_aet[z+1].ymax;g_aet[z].x=g_aet[z+1].x;g_aet[z].delat=g_aet[z+1].delat;g_aet[z+1].ymax=temp.ymax;g_aet[z+1].x=temp.x;g_aet[z+1].delat=temp.delat;}}}for(j=0;j<=9;j++){ if(g_aet[j].ymax==0) break; }j--;for(p=0;p<=j;p++){ a++;if(a%2!=0)b=g_aet[p].x;else{for(c=ZUO(b);c<=YOU(g_aet[p].x);c++)putpixel(c,i,2);}}for(t=0;t<=j;t++){ if(g_aet[t].ymax==(i+1)){ g_aet[t].ymax=0;g_aet[t].x=0;g_aet[t].delat=0;}g_aet[t].x+=g_aet[t].delat;}for(t=0;t<=j;t++){ for(z=0;z<=j-1;z++){if(g_aet[z].x<g_aet[z+1].x){ temp.ymax=g_aet[z].ymax;temp.x=g_aet[z].x;temp.delat=g_aet[z].delat;g_aet[z].ymax=g_aet[z+1].ymax;g_aet[z].x=g_aet[z+1].x;g_aet[z].delat=g_aet[z+1].delat;g_aet[z+1].ymax=temp.ymax;g_aet[z+1].x=temp.x;g_aet[z+1].delat=temp.delat;}}}}}void generate(){int i,y,n=1,m,q,p;float x;for(i=0;i<=9;i++){if(n==1){ point2.x=point1.x=300;point2.y=point1.y=200;n++;}else{ if(n%2==0){ x=40*cos(i*pi/5)+200;y=40*sin(i*pi/5)+200;}else{ x=100*cos(i*pi/5)+200;y=100*sin(i*pi/5)+200;}if(point1.y==y) { n++; continue;}m=MIN(point1.y,y);if(x==point1.x){ dge[i-1].delat=0;dge[i-1].ymax=MAX(point1.y,y);dge[i-1].x=x;dge[i-1].pedge=0;for(q=0;q<=9;q++){ if(g_et[q].n==m) break;}if(q==10){g_et[i-1].pedge=&dge[i-1];g_et[i-1].n=m;}else{g_et[q].pedge->pedge=&dge[i-1];g_et[i-1].n=0;}}else{dge[i-1].delat=(float)(x-point1.x)/(y-point1.y);dge[i-1].ymax=MAX(point1.y,y);if(point1.y>y) dge[i-1].x=x;else {dge[i-1].x=point1.x; }dge[i-1].pedge=0;for(q=0;q<=9;q++){ if(g_et[q].n==m) break;}if(q==10){ g_et[i-1].pedge=&dge[i-1];g_et[i-1].n=m;}else{g_et[q].pedge->pedge=&dge[i-1];g_et[i-1].n=0;}}p=MAX(point1.y,y);k=MIN(k,m);l=MAX(l,p);point1.x=x;point1.y=y;n++;}}if(point1.y==point2.y) return;else{if(point2.x==point1.x){dge[i-1].delat=0;dge[i-1].ymax=MAX(point1.y,point2.y);dge[i-1].x=point2.x;}else{ dge[i-1].ymax=MAX(point1.y,point2.y);if(point1.y>point2.y) dge[i-1].x=point2.x;else {dge[i-1].x=point1.x;}dge[i-1].delat=(float)(point2.x-point1.x)/(point2.y-point1.y);}}m=MIN(point1.y,point2.y);k=MIN(k,m);l=MAX(l,dge[i-1].ymax);g_et[i-1].n=m;g_et[i-1].pedge=&dge[i-1];}void main(){ int driver=DETECT,mode; int i; registerbgidriver(EGA VGA_driver);initgraph(&driver,&mode,"\\tc");initgraph(&driver,&mode,"\\tc");for(i=0;i<=9;i++){ g_aet[i].ymax=0; g_aet[i].x=0; g_aet[i].delat=0;g_et[i].pedge=0;}generate();draw1();circle(200,200,100); circle(200,200,40);getch();closegraph();}。

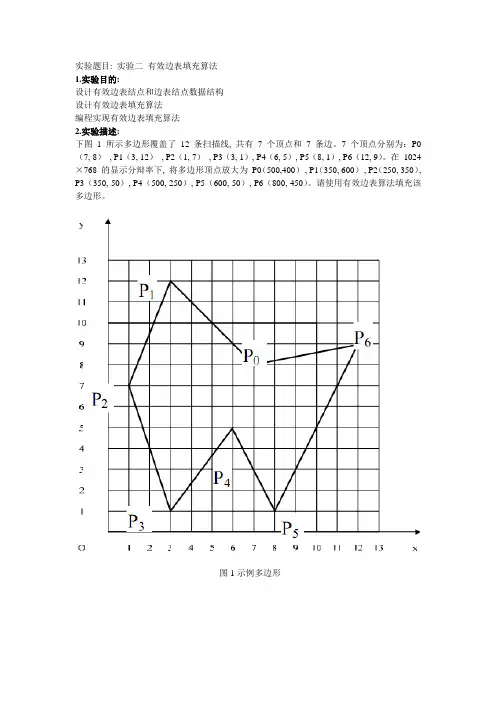
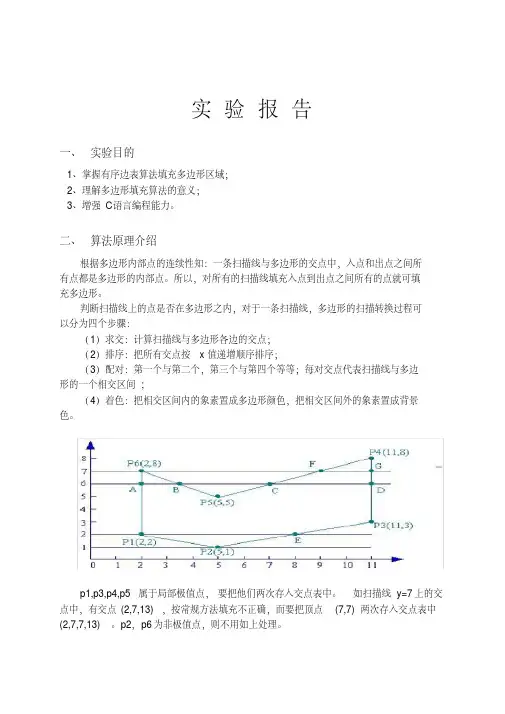
实验题目: 实验二有效边表填充算法1.实验目的:设计有效边表结点和边表结点数据结构设计有效边表填充算法编程实现有效边表填充算法2.实验描述:下图 1 所示多边形覆盖了12 条扫描线, 共有7 个顶点和7 条边。

7 个顶点分别为：P0（7, 8）, P1（3, 12）, P2（1, 7）, P3（3, 1）, P4（6, 5）, P5（8, 1）, P6（12, 9）。

在1024×768 的显示分辩率下, 将多边形顶点放大为P0（500,400）, P1（350, 600）, P2（250, 350）, P3（350, 50）, P4（500, 250）, P5（600, 50）, P6（800, 450）。

请使用有效边表算法填充该多边形。

图1示例多边形图2 屏幕显示多边形3.算法设计:（1）建立AET和BUCKET类；（2）初始化桶, 并在建立桶结点时为其表示的扫描线初始化为带头结点的链表；（3）对每个桶结点进行循环, 将桶内每个结点的边表合并为有效边表, 并进行有效边表循环；（4）按照扫描线从小到大的移动顺序, 计算当前扫描线与多边形各边的交点, 然后把这些交点按X值递增的顺序进行排序, 配对, 以确定填充区间；（5）用指定颜色点亮填充区间内的所有像素, 即完成填充工作。

4.源程序:1)//AET.hclass AET{public:AET();virtual ~AET();double x;int yMax;double k;//代替1/kAET *next;};//AET..cppAET::AET(){}AET::~AET(){}2) //Bucket.h#include "AET.h"class Bucket{public:Bucket();virtual ~Bucket();int ScanLine;AET *p;//桶上的边表指针Bucket *next;};// Bucket.cppBucket::Bucket(){}Bucket::~Bucket(){}3)//TestView.h#include "AET.h"//包含有效边表类#include "Bucket.h"//包含桶类#define Number 7//N为闭合多边形顶点数, 顶点存放在整型二维数组Point[N]中class CTestView : public CView{。

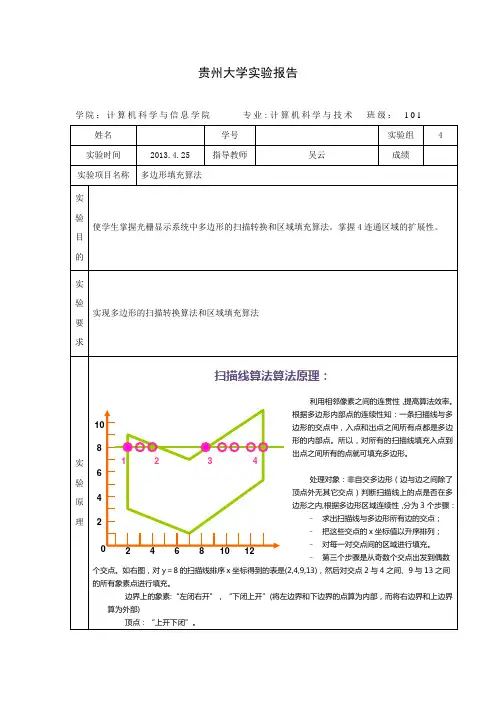
多边形填充算法-有序边表法（扫描线算法）1.算法的基本思想（扫描线连贯性原理）： 对于⼀个给定的多边形，⽤⼀组⽔平(垂直)的扫描线进⾏扫描，对每⼀条扫描线均可求出与多边形边的交点，这些交点将扫描线分割成落在多边形内部的线段和落在多边形外部的线段；并且⼆者相间排列。

于是，将落在多边形内部的线段上的所有象素点赋以给定的⾊彩值。

算法中不需要检验每⼀个象素点，⽽只考虑与多边形边相交的交点分割后的扫描线段。

2.算法求解：对于每⼀条扫描线的处理：1）求交点：⾸先求出扫描线与多边形各边的交点；2）交点排序：将这些交点按X坐标递增顺序排序；3）交点匹配：即从左到右确定落在多边形内部的那些线段；4）区间填充：填充落在多边形内部的线段。

3.求交点的⽅法最简单的办法：将多边形的所有边放在⼀个表中，在处理每条扫描线时，从表中顺序取出所有的边，分别求这些边与扫描线的交点。

不使⽤该⽅法的原因：将做⼀些⽆益的求交点动作，因为扫描线并不⼀定与多边形的边相交，扫描线只与部分甚⾄较少的边相交；因此，在进⾏扫描线与多边形边求交点时，应只求那些与扫描线相交的边的交点。

确定与扫描线相交的边：⽤边表来确定哪些边是下⼀条扫描线求交计算时应该加⼊运算的。

4.边表（ET）：ET的意义在于为扫描线提供待加⼊的新边信息。

建⽴边的分类表ET(Edge Table)，每个结点结构如下：（Ymax ，ΔX ，X Ymin，）Ymax：边的最⼤Y值；ΔX：从当前扫描线到下⼀条扫描线之间的X增量（dX/ dY)；X Ymin：边的下端点的X坐标；next：指针，指向下⼀条边。

边的分类表可以这样建⽴：先按下端点的纵坐标(y值)对所有边作桶分类，再将同⼀组中的边按下端点X坐标递增的顺序进⾏排序, X坐标还相同的按ΔX递增的顺序进⾏排序。

5.活性边表AET把与当前扫描线相交的边称活化边AEL(Active Edge List) 。

组成的表称为活性表AET，其数据域组成如下：Ymax ：存放边的上端点Y坐标；X ：边与当前扫描线交点的X坐标；ΔX ，next指针：同边表。