当前位置：文档之家 › 广义高斯求积公式的渐进计算与数表

广义高斯求积公式的渐进计算与数表

  • 格式：docx
  • 大小：36.82 KB
  • 文档页数：1

下载文档原格式

  / 1

合集下载

Gauss型求积公式

Gauss型求积公式

Gauss型求积公式 一、Gauss型求积公式 定义： 个节点的具有2 定义 ： 把具有 n＋1 个节点的具有 2 n+1 次代 数精确度的插值型求积公式
∫
b
a
f (x)dx ≈ ∑A f (xk ) k
k=0
n
称为Gauss型求积公式， 称为Gauss型求积公式，其求积节点 xk k=0， Gauss型求积公式 （ =0， 称为高斯点 高斯点， 高斯系数。 1，……n）称为高斯点，系数 A 称为高斯系数 k称为高斯系数 Remark：构造Gauss Gauss型求积公式的关键在于确定高斯 Remark：构造Gauss型求积公式的关键在于确定高斯 个高斯点构造基函数， 点，再由n＋1个高斯点构造基函数，从而得到高斯 系数。 系数。
f (x) = P x) n+1(x) ( ω 的次数不超过2n+1。
故有
∫ω
a
b
n+1
( x )P( x )dx = ∑A ωn+1( xk )P( xk ) = 0 k
k=0
n
充分性 ： 设 ∫ ωn+1(x)P(x)dx = 0 对于任意次数不超过 a ω 2n+1的多项式 f (x),设 n+1(x)除f(x)的商为p(x),余 项为q(x)。
Ak 0.1713244924 0.3607615730 0.4679139346 0.1294849662 0.2797053915 0.3818300505 0.4179591837 0.1012285363 0.2223810345 0.3137066459 0.3626837834
6
7 4 0.3478548451 0.6521451549

4。4高斯型求积公式

4。4高斯型求积公式

=
A
1
=1
于是得到求积公式
华长生制作
∫
1 −1
f
( x )dx
≈ f −
1 + f 3
1 3
3
它有3次代数精度， 它有 次代数精度，而以两个端点为节点的梯形公式只有 次代数精度 1次代数精度。 次代数精度。 次代数精度 一般地， 一般地，考虑带权求积公式
I =
∫
1
0
x 2 e x dx
解 由于区间为[0,1],所以先作变量替换 由于区间为 所以先作变量替换x=(1+t)/2,得 得 所以先作变量替换 2 1 1 1 2 x I = ∫ x e dx = ∫ (t +1 e(1+t ) / 2dt ) 0 8 −1 2 对于n=1,由两点 由两点Gauss-Legendre公式有 令 由两点 公式有 f (t ) = (1 + t ) e (1+t )/ 2 对于
∫
b a
ρ
( x )l k ( x )dx
, k = 0 ,1 , L n
是关于Gauss点的 点的Lagrange插值基函数。 插值基函数。 其中 l k ( x ) 是关于 点的 插值基函数
华长生制作
10
定理2 定理 高斯型求积公式总是稳定的。 证明 只需证明高斯系数全为正即可。由 于插值公式对次数不超过2n+1的多项式精 f ( x ) = lk2 ( x), 其中lk ( x ) 是n次拉格 确成立，若取 朗日插值基函数，有
1 P3 ( x ) = ( 5 x 2 − 3 x ), 当n=2时，三次 时 三次Legendre多项式 多项式 2
零点为 x 0

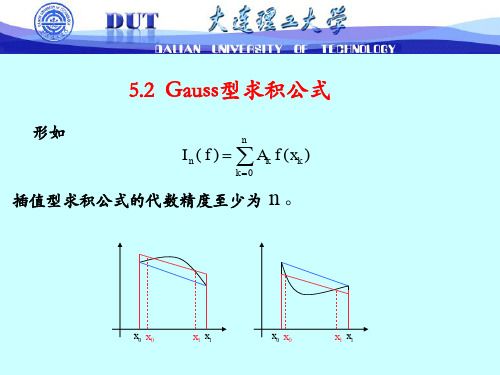
Gauss型求积公式-第5章

Gauss型求积公式-第5章
5.2 Gauss型求积公式
形如
I n ( f ) Ak f ( xk )
k 0 n
插值型求积公式的代数精度至少为
n。
x0 x0
x1 x1
x0 x0
x1 x1
两点的求积公式为： 1 f ( x) dx A0 f ( x0 ) A1 f ( x1 ) 若限制等距节点，则 1、x0 , x1固定，A0 , A1 变量 2、确定 A0 , A1 需两个方程
x0 , x1 ,, xn 是Gauss点 x0 , x1 ,, xn 是Gauss点
n 1 ( x) 是正交多项式。
x , x ,, x
0 1
n
是正交多项式的根。
证明： 必要性
I ( f ) ( x) f ( x)dx
a
b
I n ( f ) Ak f ( xk )
n n 2
n 1 ( xk ) 1 ( x ) ( x xk ) f ( xk ) n 1 k
2
n 1 ( x) ( x xk ) f ( xk ) 1 ( xk )( x xk ) k 0 n

1
1
f ( x) dx
1 1 f f 3 3
对于任意区间 a, b 上权函数 x 1 的Gauss型求积公式，只需 作变量替换：
x
则有
x a, b t 1, 1 ，这样
ab ba t 2 2
n 1 ( xk ) f ( xk ), k 0,1,..., n H 2 n 1 ( xk ) f ( xk ), H 2
的2n+1次Hermite插值多项式，即（P110 例5）

《高斯求积公式》课件

《高斯求积公式》课件
通过选取特定的节点和权重，可以准确计算 被积函数的定积分。
2 它具有高精度、广泛适用和简单高
效的特点。
在科学计算、工程分析和统计建模等领域得 到广泛应用。
重。
3
发展背景
高斯求积公式最早由数学家高斯在19世 纪提出，用于解决天文学和天体力学中 的复杂了突破 性进展，为后来的科学研究提供了强大 的计算工具。
基本思想和原理
节点选取
高斯求积公式通过选取特定的节点，使得积分 计算更加准确和高效。
积分逼近
通过对节点和权重进行适当的组合和加权，高 斯求积公式可以逼近被积函数的定积分。
《高斯求积公式》PPT课 件
探索高斯求积公式的应用前景，了解它的重要性和实用性，以及如何利用该 公式进行数值积分计算。
概述
高斯求积公式是一种用于数值积分的方法，通过等距离选取节点和节点处对 应的权重，可以准确地计算被积函数的定积分。
由来和历史
1
发现过程
2
高斯通过计算多项式的根和权重的方法，
发现了一组可用于数值积分的节点和权
积分计算
通过将插值多项式代入定积分公 式，可以推导出高斯求积公式的 数学表达式。
优点和适用范围
高精度
高斯求积公式具有很高的数 值精度，适用于对精确积分 结果要求较高的情况。
广泛应用
高斯求积公式在科学计算、 工程分析和统计建模等领域 都有广泛的应用。
简单高效
使用高斯求积公式进行数值 积分计算相对简单，并且有 较高的计算效率。
权重计算
对于每个节点，高斯求积公式还会计算相应的 权重，以保证被积函数的积分结果更加精确。
误差分析
高斯求积公式的误差分析可以帮助我们评估和 控制数值积分的精度和可靠性。

高斯求积公式-数值分析课程设计2

高斯求积公式-数值分析课程设计2

一、 引言介绍高斯型求积公式，并使用其求积分⎰=1sin I xdx 。

要求：数值实验结果要体现出随高斯点的增加误差的变化。

我们知道,求积公式⎰∑=≈bani i ix f Adx x f 0)()( （1.1）含有22+n 个待定常数i x 及),,2,1,0(n i A i =,如果它具有n 次代数精确度,则它应使1+m 个方程mk dx x x A bakni ki i ,,2,1,0,==⎰∑= (1.2)精确成立。

作为插值型求积公式(1.1)它至少具有n 次代数精确度；另一方面,令)())(()(101n n x x x x x x x ---=+ ω,则对22+n 次多项式)()(21x x f n +=ω而言，(7.5.1)右端为零,而左端严格大于零,即(7.5.1)式对22+n 次多项式)(21x n +ω不准确成立。

但要确定方程组(7.5.2)中的22+n 个待定常数i x 与i A ,最多需要给出22+n 个独立条件,所以m最大取12+n 。

因此,插值型求积公式(1.1)的代数精确度最小是n ,最大是12+n ．由此可见，高斯公式的代数精度比牛顿-科特斯公式高，求解高斯求积公式的关键就是解出上述2n+2个待定常数。

为解决上述问题，首先要先给出三个定理：定理一：以n x x x ,,,10 为节点的插值型求积公式(7.5.1)具有12+n 次代数精确度的充要条件是以这些节点为零点的多项式)())(()(101n n x x x x x x x ---=+ ω与任意次数不超过n 的多项式)(x P 均在区间],[b a 上正交,即⎰=+ban dx x x P 0)()(1ω (1.3)定理二：高斯公式(1.1)的求积系数k A 全为正,且nk dx x l dx x l A bak bak k ,1,0,)()(2===⎰⎰(1.4)定理三：对于高斯公式(1.1),其余项为dxx fn f R ban n ⎰+++=)()()!22(1)(21)22(ωη (1.5)其中).())(()(],,[101n n x x x x x x x b a ---=∈+ ωη证明 以n x x x ,,,10 为节点构造)(x f 的埃尔米特插值多项式)(x H),()(i i x f x H = ni x f x H i i ,1,0),()(='='因为)(x H 是12+n 次多项式,而它的余项是)()()!22(1)()(21)22(x fn x H x f n n +++=-ωξ所以高斯公式(7.5.1)对)(x H 能准确成立,即∑∑⎰====ni i in i iibax f Ax H A dx x H 0)()()(从而dxx fn dxx H dx x f x f A dx x f f R n ban babani i i ba)()()!22(1)()()()()(21)22(0++=⎰⎰⎰∑⎰+=-=-=ωξ若)()22(x fn +在区间],[b a 上连续,由于)(21x n +ω在],[b a 上不变号,故应用积分中值定理可得],[,)()()!22(1)(21)22(b a dx x fn f R ban n ∈+=⎰++ηωη上述定理说明,与牛顿—科兹公式进行比较,高斯公式不但具有高精度,而且它还是数值稳定的,但是节点和求积系数的计算比较麻烦。

数值分析课件高斯求积公式

数值分析课件高斯求积公式

1
1
1 f ( x)dx A0 f (
求 A0 , A：1
3 ) A1 f (
) 3
令 f ( x) ，1,代x入公式精确成立，得到： A0 A1 1
或
1
1
A0 1 l0 ( x)dx 1, A1 1 l1( x)dx 1
两点Gauss-Legendre求积公式
3次代数精度
1
1
1
一、 Gauss积分问题的提法
n
积分公式的一般形式： In ( f ) Ak f ( xk ) k0
➢为了提高代数精度，需要适当选择求积节点:
①当求积节点个数确定后，不管这些求积节点如何选
取，求积公式的代数精度最高能达到多少？2n 1
②具有最高代数精度的求积公式中求积节点如何选取？
n 个1求积节点， n个求1 积系数，共 个2n未知2量，需要
f p max f p axb
则Gauss型求积公式（*）是收敛的。
证明：由Weierstrass定理知 对 0
存在m次多项式 p( x满)足
下证 N , 当 n 时N
f
p 2
b
( x)dx
a
b
n
f ( x)( x)dx
a
Ak f ( xk )
k0
b
n
f ( x)( x)dx
➢ Gauss-Chebyshev求积公式
(x)
1
n
f ( x)( x)dx
1
Ak f ( xk )
k0
1 1 x2
其中求积节点
多项式的零点
xk
n [a, b] 是n+1次Chebyshev
k0

4.3 高斯积分

4.3 高斯积分

节点xk 及求积系数 Ak 的选取方法
由特殊函数理论知，勒让德（Legendre）多项式
1 dn p n ( x) = n ⋅ n [( x 2 − 1) n ] 2 n! dx
在[-1，1]上是正交的，即 1 ∫Байду номын сангаас1 pn ( x) pn+1 ( x)dx = 0
[2(n + 1)]! p n+1 ( x )的首项系数为： n+1 ，故常取 2 [(n + 1)!]2
三点(n=2)高斯法计算子程序 subroutine Gauss(a,b,G) dimension t(3),w(3) data t/0.,0.774597,-0.774597/ data w/0.888889,0.555556,0.555556/ G=0.0 1 1 x = (b + a) + (b − a)t do 10 i=1,3 2 2 x=0.5*[(b+a)+(b-a)*t(i)] n 1 10 G=G+w(i)*f(x) ∫−1 f ( x)dx ≈ ∑ Ak f ( xk ) k =0 G=0.5*(b-a)*G return b−a f ( x)dx = ∫ ∫ ϕ (t )dt end 2
以上讨论中，积分区间为[-1,1]。 当实际计算区间为 [a, b] ,可采用如下变量替换：
1 1 x = (b + a) + (b − a)t 2 2
则积分区间 [a, b] 变为[-1,1]，且积分变为：
∫
b
a
b−a 1 f ( x)dx = ∫−1ϕ (t )dt 2
a+b b−a + t) 其中 ϕ (t ) = f ( 2 2

高斯求积公式

高斯求积公式

总结
1：梯形求积公式和抛物线求积公式是低精度的方法，但对于光滑 性较差的函数有时比用高精度方法能得到更好的效果。复化梯形 公式和抛物线求积公式，精度较高，计算较简，使用非常广泛。 2：Romberg求积方法，算法简单，当节点加密提高积分近似程度 时，前面的计算结果可以为后面的计算使用，因此，对减少计算 量很有好处。并有比较简单的误差估计方法。 3。Gauss型求积，它的节点是不规则的，所以当节点增加时，前 面的计算的函数值不能被后面利用。计算过程比较麻烦，但精度 高，特别是对计算无穷区间上的积分和旁义积分，则是其他方法 所不能比的。
n
证明： 时代入公式， 证明：分别取 f(x)=1, x，x2，...xn 时代入公式，并让其成为等式得 ，
A1 + A2 + …… + An =∫ab1dx.= b-a +xn An =∫abxdx.= （b2-a 2)/2 ...... x1 rA1 + x2 rA2+ …… +xn rAn =∫abxr dxr =(br+1-a r+1)/ (r+1) 等式， 个待定系数 变元),要想如上方程组有唯一解 个待定系数(变元 要想如上方程组有唯一解， 上式共有 r 个 等式，2n个待定系数 变元 要想如上方程组有唯一解，应有方 程组中方程的个数等于变元的个数,即 程组中方程的个数等于变元的个数 即 r=2n,这样求出的解答应的求积公式的代 这样求出的解答应的求积公式的代 数精度至少是2n-1,下面证明代数精度只能是2n-1. 下面证明代数精度只能是 数精度至少是 下面证明代数精度只能是 [ 如果事先已选定 ，b]中求积节点 k如下a≤x1 ≤…x n≤b,上式成为 个未知 如果事先已选定[a 中求积节点x 上式成为n个未知 中求积节点 如下 ≤ 上式成为 元线性方程组， 时方程组有唯一解 有唯一解] 数 A1、...An的n元线性方程组，此时要 元线性方程组 此时要r=n 时方程组有唯一解 、 x1 A1 + x2 A2+ ……

4。4高斯型求积公式

4。4高斯型求积公式

华长生制作
19
例 计算积分

1
1
2 x dx 2 1 x
解 选用n=2的Gauss-Chebyshev求积公式计算,这时 f x 2 x 于是有
2 x 2 3 dx 1 x2 3 2 3 4.368939556 2 2

1
1
2
15
华长生制作
Ak 4-4。 Guass-Legendre求积公式中的Gauss点和求积系数见书上表 k
对于一般区间[a，b]上的求积，如果用Gauss-Legendre求积公式，那么
x
必须作变量替换
1 1 x a b b a t 2 2
，并有
使 x
[a , b ] 时，t [ 1,1]
书上表4.6给出了部分高斯-拉盖尔求积公式的 节点和系数。
华长生制作 22
4. 高斯-埃尔米特求积公式
x
的零点，称这样的高斯型求积公式为高斯-拉盖尔 求积公式，其表示式为

华长生制作

0
e x f x dx Ak f xk
k 0
21
n
其中
[(n 1)!]2 Ak 1 ( xk )]2 xk [ Ln (k 0,1, , n)
截断误差为
[(n 1)!]2 (2 n 2) R[ f ] f ( ), (0, ) (2n 2)!
14
当n=0时，一次Legendre多项式x的零点为0， Ak 为2；
当n=1时，二次Legendre多项式 零点为 x0
1 1 , x1 3 3
P 2 x
1 (3 x 2 1), 2
, Ak 为1（k=0,1) ;

Gauss 求积公式 - mathecnueducn

Gauss 求积公式 - mathecnueducn
积分区间: [-1, 1]，权函数: ρ ( x ) =
1 1 − x2
Gauss 点 = Chebyshev 多项式 Tn+1(x) 的零点 G-C 求积公式:
∫
1 −1
1 1 − x2
f ( x ) dx ≈ ∑ Ai f ( xi )
i =0
21
n
G-C 公式
Tn+1(x) 的零点
3
Gauss 型求积公式
怎样构造更高精度的求积方法
考虑求积公式
∫
b a
f ( x )dx ≈ ∑ Ai f ( xi )
i =0
n
含 2n+2 个参数 (节点与系数)，为了使该公式具有 尽可能高的代数精度，可将 f (x) = 1, x, x2, …, x2n+1 代入公式，使其精确成立，则可构造出代数精度至 少为 2n+1 的求积公式! 自由选取求积节点！等分点不一定最佳！
第四章 数值积分与数值微分
— Gauss 求积公式
1
内容提要
数值积分 基本概念 Newton-Cotes 求积公式 复合求积公式 Gauss 求积公式 Romberg 求积公式 多重积分 数值微分
2
本讲内容
Gauss 求积公式
一般理论：公式，余项，收敛性，稳定性 Gauss-Legendre 求积公式 Gauss-Chebyshev 求积公式 无限区间的 Gauss 求积公式
17
G-L 公式余项
余项公式
f ( 2 n+ 2) (η ) b 2 R[ f ] = Pn+1 ( x ) dx ∫ (2n + 2)! a
( n + 1)!] [ = 3 (2n + 3) [(2n + 2)!] 2

高斯求积公式

高斯求积公式

(2 5
(2 7
2
3 2
5
x0 ) x1 x0 ) x1
2; 7 2. 9
进一步整理得
2
5 2
7
( x0 ( x0
x1 ) x1 )
2
3 2
5
x0 x1 x0 x1
2; 7 2. 9
由此解出
从而
x0 x1
5, 21
x0
x1
10 9
,
7
x0 0.821162, A0 0.389111,
2
构造求积1公式
3
1
1 f ( x)dx A0 f (
1 3
)
A1
f
(
1 ), 3
18
令它对 f (x) 都1,准x 确成立，有
A0 A0
A1 1 3
2;
A1
1 0. 3
由此解出 A0 A1 1, 从而得到两点高斯-勒让德求积公式
1 f ( x)dx f ( 1 ) f ( 1 ).
当积分区间不是 [，1,而1]是一般的区间 时[a，, b]
只要做变换
22
x bat ab,
2
2
可将 [a,化b]为 [,1,1] 这时
b f (x)dx b a 1 f b a t a b dt. （5.10）
a
2 1 2
2
对等式右端的积分即可使用高斯-勒让德求积公式.
23
例6 用4点n( 3)的高斯-勒让德求积公式计算
Ak (k 0,1,, n).
下面讨论高斯求积公式(5.1)的余项.
利用 f在(x节) 点 即 H 2n1,
xk (k 的0埃,1,尔米, n特)插值

广义高斯求积公式的渐进计算与数表

广义高斯求积公式的渐进计算与数表

广义高斯求积公式的渐进计算与数表
广义高斯求积公式是一种用于数值积分的方法，可以在给定有限个节
点上对任意函数进行近似积分。

该公式适用于广泛的函数类，例如多项式、指数和三角函数等。

在计算机科学和工程领域，广义高斯求积公式常被用
于求解复杂的数值积分问题。

∫(a到b)w(x)f(x)dx ≈ ∑(i=0到n)wi*f(xi)
其中，a和b是积分区间的端点，w(x)是权重函数，f(x)是待求函数。

n是节点的数量，wi和xi分别是第i个节点的权重和位置。

广义高斯求积公式的核心思想是通过合适的节点和权重来近似代替被
积函数，使得积分结果尽可能接近准确值。

节点的选择通常采用在积分区
间上具有优良性质的多项式。

权重的选择则需要满足一定的条件，以确保
公式的稳定性和准确性。

广义高斯求积公式的渐进计算方法通常基于节点的递推关系。

对于给
定的节点和权重，可以通过递推公式快速计算出更多节点和权重的数值。

递推公式的具体形式取决于所使用的多项式族，例如勒让德多项式、拉盖
尔多项式或切比雪夫多项式等。

广义高斯求积公式的渐进计算和数表对于数值积分的高效求解非常重要。

通过递推计算和直接查表，可以避免重复的节点和权重计算，提高计
算效率。

数表则为用户提供了灵活、方便的方法，使得人们能够更快速地
进行数值积分计算，加快科学研究与工程实践的进程。

总之，广义高斯求积公式的渐进计算和数表为数值积分问题的求解提
供了有效的方法和工具。

这些方法和资源可以帮助人们更高效地求解复杂
的数值积分问题，促进科学研究和工程实践的发展。

高斯型求积公式课件

高斯型求积公式课件

自编程实现
要点一
理解高斯型求积公式的原理
在自编程实现高斯型求积公式时，需要深入理解高斯型求 积公式的原理和数学推导过程，以确保编程实现的正确性 。
要点二
编写代码并进行测试
根据高斯型求积公式的原理，编写相应的代码并进行测试 ，以确保代码的正确性和可靠性。在编写代码时，需要注 意代码的可读性和可维护性，以提高代码的质量和可复用 性。
收敛性分析
对高斯型求积公式的收敛性进行深入分析，有 助于进一步优化其收敛速度。
稳定性
在提高收敛速度的同时，保持高斯型求积公式的稳定性是关键。
高斯型求积公式的并行化改的计算过程分解为多个子任务
，可以实现并行计算，进一步提高计算效率。
并行算法设计
02 设计高效的并行算法是实现高斯型求积公式并行化的
在微积分基本定理推导过程中，我们需要理解微积分的基本 概念和定理的证明过程，以确保推导的正确性和可靠性。
数值积分公式推导
数值积分公式是高斯型求积公式的另一种形式，通过数值积分公式的推导，我们可以将高斯型求积公 式应用到数值计算中。
在数值积分公式推导过程中，我们需要理解数值计算的基本原理和方法，以确保数值计算的准确性和 可靠性。
03
高斯型求积公式的实现
编程语言实现
Python实现
Python是一种通用编程语言，具有简洁的语法和丰富的科学计算库。使用Python实现高斯型求积公式可以充分 利用NumPy等科学计算库，提高计算效率。
C实现
C是一种高效的系统编程语言，适合进行大规模数值计算。通过C实现高斯型求积公式，可以充分利用其编译型语 言的性能优势，提高计算速度。
高斯型求积公式具有高精度、高稳定 性和易于实现等优点，因此在数值计 算中得到了广泛应用。

第四节 高斯Gauss求积公式讲解

第四节 高斯Gauss求积公式讲解

Ak f ( x k )
k?0
的代数精度最高为 2n+1次。
证明：取特殊情形 ? ( x ) ? 1,
分别取 f(x)=1, x ，x2，...xr 代入公式，并让其成为
等式，得：
A0 + A1 + …… + A n =∫ab1dx.= b-a
x0 A0 + x1 A1+ …… +x n An =∫abxdx.= （b2-a 2)/2
? ? ? 于是
1 f ( x )dx ? 1
1
f
(
1
(1
?
t ))dt
?
?
1
1
F (t )dt
0
2 ?1 2
2 ?1
? 由两点Gauss? Legendre求积公式
1
F (t)dt ? F (?0.577)? F(0.577)
?1
得
1
11 1
11
11
? ? f (x)dx ? f ( (1? t))dt ? f ( (1? 0.577))? f ( (1? 0.577))
0
2 ?1 2
22
22
数值分析
数值分析
? 例 对积分 1 f ( x )dx，试利用 n ? 3的四点 Gauss ? Legendre 0 求积公式构造 Gauss型求积公式。即确定 x 0 , x1 , x2 , x3和 A0 , A1 , A2 , A3使 1 ?0 f ( x )dx ? A0 f ( x0 ) ? A1 f ( x1 ) ? A2 f ( x2 ) ? A3 f ( x3 ) 为 Gauss 型求 积公式。
3）对任意一个次数 ≤n-1 的多项式P(x)，有

Gauss型求积公式

Gauss型求积公式
ab ba x t 2 2
即可将区间[a,b]变换到[-1,1]上：

b
a
1 ba 1 ab ba f ( x )dx f( t )dt (t )dt 1 2 1 2 2
n 1 2 3
xk 0 ±0.5773502692 ±0.7745966692 0 ±0.8611363116 ±0.3399810436
四、Gauss-Laguerre求积公式
区间[0,)上权函数W(x)=e-x的Gauss型求积公式,称为GaussLaguerre求积公式,其Gauss点为Laguerre多项式的零点.
公式的Gauss点和求积系数可在数学用表中查到 . 由
0 f ( x)dx 0 e e f ( x)dx
2 (1 xk ) Pn'1 ( xk ) 一点Gauss-Legendre求积公式为：

1
1
f ( x)dx Ak f ( xk )
k 0
n
Ak

2

2
(k 0,1,, n)

1
1
1
f ( x )dx 2 f (0)
两点Gauss-Legendre求积公式为：
3 3 1 f ( x)dx f ( 3 ) f ( 3 )
故有

b
a
n1 ( x )P ( x )dx Ak n1 ( xk )P ( xk ) 0
k 0
n
充分性 ：
设a n1 ( x) P( x)dx 0 对于任意次数不超过 n 1 ( x)除f(x)的商为p(x),余 2n+1的多项式 f ( x), 设 项为q(x)。
x x

第3节 Gauss型求积公式

第3节 Gauss型求积公式


3．Laguere（拉盖尔）多项式
dn n x Ln ( x ) e x n ( x e ), 0 x , n 0,1, 2, dx
为区间[0,+ ∞)上关于权函数ρ(x)=e -x 的正交多项式。 而且 Ln(x) 的首项系数为 (-1)n 。具有性质：
(1). ( Lm , Ln )
得到 n-1 次插值多项式及误差：
n (x x ) i f ( x) f ( xk ) f [ x , x1 , x2 ,, xn ] n ( x ) i 1 k 1 i k ( x k x i )
n
两端积分得到：
n ( x ) ( x x1 )( x x2 )( x xn )
( x ), x [a , b]
则称多项式族 { gk(x)} 在[a,b]上带权ρ(x) 正交，并称gn(x) 为[a,b]上带权ρ(x) 的 n 次正交多项式。
1 1] 例如： 1, x , x , 在 [1， 上带权 ( x ) 1 正交。 3 gk ( x ) * , 则称其为首项系数为1的多项式， 令： gk ( x ) Ak
( x ) 1 x 2 , x [1,1]
2、正交多项式
对于多项式序列
gn ( x ) An x An1 x
n
n 1
A1 x A0 , n 0,1,2 ,
及权函数 如果：

b
a
0, l m, ( x ) gl ( x ) gm ( x )dx b 2 ( x ) gm ( x )dx 0, l m a
4.Hermite多项式
是区间(-∞,+∞)上关于权函数 ( x ) e 的正交多项 式。而且 Hn(x) 的首项系数为 2n ,具有性质：

Gauss型求积公式

Gauss型求积公式
性质
Gauss型求积公式具有高精度和高效性，特别是对于一些特殊函数（如多项式函数）的积分，其精度更高。此外， Gauss型求积公式还具有对称性、规范性和最优性等性质。
Gauss型求积公式的分类
01
按照节点数分类
根据使用的节点数不同，可以将Gauss型求积公式分为一 元、二元和多元等类型。一元Gauss型求积公式使用一个 节点，二元Gauss型求积公式使用两个节点，以此类推。
Gauss型求积公式
• 引言 • Gauss型求积公式的基本概念 • Gauss型求积公式的构造方法 • Gauss型求积公式的误差分析 • Gauss型求积公式的应用实例 • 结论
01
引言
背景介绍
01
Gauss型求积公式是数值分析中的一种重要方法，主要用于解决 积分问题。
02
它以德国数学家Carl Friedrich Gauss的名字命名，是数值积分
工程设计
在工程设计中，Gauss型求积公 式可用于计算几何形状的面积、 体积等，以及优化设计参数。
金融工程
在金融工程中，Gauss型求积 公式可用于计算期权定价、风 险评估等金融衍生品的价值。
02
Gauss型求积公式的基本概念
定义与性质
定义
Gauss型求积公式是一种数值积分方法，用于近似计算定积分的值。它通过选择一组特定的节点和权重，将积分 区间划分为有限个小区间，然后利用这组节点和权重来逼近积分。
02
Gauss型求积公式具有高精度和高效率的特点，能够 快速准确地计算积分。
03
它能够减小误差，提高计算精度，特别适合处理复 杂函数积分问题。
结论 Gauss型求积公式的优点与局限性
局限性
Gauss型求积公式需要预先确定节点和权重，对于某些复杂函数可能难以 找到合适的节点和权重。

高斯求积公式

高斯求积公式

高斯求积公式
高斯求积公式，又称为高斯积分公式，是由18世纪德国数学家卡尔·高斯发现的重要的定积分计算公式。

它是用来计算一元函数定积分的有效方法，是数学计算中最重要的积分公式。

高斯求积公式包括两种不同的形式：一种叫做标准形式，另一种叫做拉格朗日形式。

两种形式的计算结果是一样的，所以可以任意使用其中一种形式来计算定积分。

标准形式的高斯求积公式为：
∫f(x)dx=Σwi*fi(xi) (i=1,2,3,…n)
其中，wi为积分权值，fi(xi)为积分点处函数值，xi为积分点，n 为积分点数。

拉格朗日形式的高斯求积公式为：
∫f(x)dx=Σwi*fi(xi)*fi'(xi) (i=1,2,3,…n)
其中，wi为积分权值，fi(xi)为积分点处函数值，fi'(xi)为积分点处函数一阶导数，xi为积分点，n为积分点数。

高斯求积公式的基本原理是：将函数拆分为多个函数，将定积分的计算拆分成多个简单的积分，然后再求和。

高斯求积公式可以计算
多项式、几何线性函数等积分，是一种十分有效的计算积分的方法。

高斯求积公式的优势在于它的公式简单，计算速度快，可以有效减少计算量，提高计算效率，使得复杂的积分可以轻松计算出来。

它也可以用来计算多元函数的积分，对于函数求积有着重要的意义。

总之，高斯求积公式是一种十分重要的定积分计算公式，可以用来计算一元函数的积分，也可以用来计算多元函数的积分，是数学计算中有效的方法。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

广义高斯求积公式的渐进计算与数表
广义高斯求积公式是一种数值积分方法，用于计算定积分。

它的基本
思想是将被积函数在积分区间上用一个多项式插值，然后将插值多项式的
系数乘以被积函数的值进行积分。

该方法的优势在于可以通过选择适当的
插值点和权重，提高数值积分的精度和效率。

∫_[a,b] (w(x)f(x))dx ≈ ∑_(i=0)^n (w_i*f(x_i))
其中，a和b是积分区间的端点，w(x)是权重函数，f(x)是被积函数，n是积分点的个数，w_i和x_i是分别对应第i个积分点的权重和插值点。

在实际计算中，广义高斯求积公式的精度和效率取决于选取的插值点
和权重。

一种常用的方法是选择Chebyshev－Gauss积分点和权重。

Chebyshev－Gauss积分点是通过对Chebyshev多项式进行零点计算得到的，这些积分点在区间[-1,1]上具有最优的插值性质。

然后，通过线性变
换将这些积分点映射到[a,b]上，并利用一些数值算法计算对应的权重。

对于高斯求积公式，常用的方法是利用数值算法进行计算，如递推关系、定点迭代和数值优化等。

这些算法可以通过计算递推关系和误差限定
理进行渐进计算，从而提高求积公式的精度和效率。

此外，还可以通过数表的方式记录已经计算好的高斯求积公式的插值
点和权重，以便快速查找和使用。

这些数表通常是在计算资源允许的情况
下通过计算机程序生成的，可以根据需要选择不同精度和积分区间的数表。

总之，广义高斯求积公式是一种有效的数值积分方法，通过选择合适
的插值点和权重，可以提高数值积分的精度和效率。

它的渐进计算和数表
记录可以通过递推关系和数值算法进行实现，以应对不同精度和积分区间
的需求。