2017-2018学年高中数学第一章立体几何初步1.5平行关系1.5.1平行关系的判定学案北师大版必修2

第1课时平行关系的判定［核心必知] 1．直线与平面的位置关系直线与平面的位置关系图形语言符号语言直线在平面内aα直线与平面相交a∩α＝A直线与平面平行a∥α2。

直线与平面平行的判定文字语言图形语言符号语言若平面外的一条直线与此平面内的一条直线平行，则该直线与此平面平行3.文字语言图形语言符号语言如果一个平面内有两条相交直线都平行于另一个平面,则两平面平行［问题思考]1．若直线a平行于平面α内的无数条直线，则直线a平行于平面α吗?提示：不一定,因为直线a在平面α内时，与a平行的直线也有无数条．2．对于平面与平面平行的判定定理中,若把“相交”去掉，这两个平面是否一定平行，为什么？提示：不一定．如图中,平面α内的两条直线a，b均平行于β，而α与β却相交．讲一讲1。

如图，在四棱锥P.ABCD中,底面ABCD是矩形,E，F分别是PB，PC的中点．证明：EF∥平面PAD。

[尝试解答］证明：在△PBC中，E,F分别是PB,PC的中点，∴EF∥BC.又BC∥AD，∴EF∥AD。

又∵AD平面PAD，EF平面PAD,∴EF∥平面PAD。

1．判断或证明线面平行的方法(1)定义法：证明直线与平面无公共点（不易操作）；（2）判定定理法：aα,bα，a∥b⇒a∥α；（3)排除法：证明直线与平面不相交,直线也不在平面内．2．证明线线平行的方法（1)利用三角形、梯形中位线的性质；(2)利用平行四边形的性质；(3)利用平行线分线段成比例定理．练一练1．如图，P是平行四边形ABCD所在平面外一点,Q是PA的中点，求证：PC∥平面BDQ.证明：连接AC交BD于O，连接QO。

∵四边形ABCD是平行四边形,∴O为AC的中点．又Q为PA的中点，∴QO∥PC。

显然QO平面BDQ，PC平面BDQ，∴PC∥平面BDQ.讲一讲2。

如图所示,正方体ABCD.A1B1C1D1中，M，N，E，F分别是棱A1B1，A1D1，B1C1,C1D1的中点．求证：平面AMN∥平面EFDB.［尝试解答] 证明：如图所示，连接MF。

北师大版高中教材目录第一章 集合§1 集合的含义与表示 §2 集合的基本关系 §3 集合的基本运算 3.1 交集与并集3.2 全集与补集第二章 函数§1 生活中的变量关系 §2 对函数的进一步认识 2.1 函数概念2.2 函数的表示法 2.3 映射§3 函数的单调性§4 二次函数性质的再研究4.1 二次函数的图像 4.2 二次函数的性质§5 简单的幂函数第三章 指数函数和对数函数 §1 正整数指数函数§2 指数扩充及其运算性质2.1 指数概念的扩充 2.2 指数运算的性质§3 指数函数3.1 指数函数的概念3.2 指数函数x y 2= 和xy ⎪⎭⎫ ⎝⎛=21 的图像和 性质3.3 指数函数的图像和性质§4 对数4.1 对数及其运算 4.2 换底公式§5 对数函数5.1 对数函数的概念 5.2 对数函数x y 2log =的图像和性质5.3 对数函数的图像和性质§6 指数函数、幂函数、对数函数增长的比较第四章 函数应用 §1 函数与方程1.1 利用函数性质判断方程解的存在 1.2 利用二分法求方程的近似解§2 实际问题的函数建模2.1 实际问题的函数刻画 2.2 用函数模型解决实际问题 2.3 函数建模案例第一章 立体几何初步 §1 简单几何体1.1 简单旋转体 1.2 简单多面体§2 直观图 §3 三视图3.1 简单组合体的三视图 3.2 由三视图还原成实物图§4 空间图形的基本关系与公理4.1 空间图形基本关系的认识 4.2 空间图形的公理§5 平行关系5.1 平行关系的判定 5.2 平行关系的性质§6 垂直关系6.1 垂直关系的判定 6.2 垂直关系的性质§7 简单几何体的面积和体积7.1 简单几何体的侧面积7.2 棱柱、棱锥、棱台和圆柱、圆锥、圆台的体积7.3 球的表面积和体积§8 面积公式和体积公式的简单应用第二章 解析几何初步 §1 直线与直线的方程1.1 直线的倾斜角和斜率 1.2 直线的方程 1.3 两条直线的位置关系 1.4 两条直线的交点1.5 平面直角坐标系中的距离公式§2 圆与圆的方程2.1 圆的标准方程 2.2 圆的一般方程2.3 直线与圆、圆与圆的位置关系§3 空间直角坐标系3.1 空间直角坐标系的建立3.2 空间直角坐标系中点的坐标3.3 空间两点间的距离公式第一章统计§1 从普查到抽样§2 抽样方法2.1 简单随机抽样2.2 分层抽样与系统抽样§3 统计图表§4 数据的数字特征4.1 平均数、中位数、众数、极差、方差 4.2 标准差§5 用样本估计总体5.1 估计总体的分别5.2 估计总体的数字特征§6 统计活动：结婚年龄的变化§7 相关性§8 最小二乘估计第二章算法初步§1 算法的基本思想1.1 算法案例分析1.2 排序问题与算法的多样性§2 算法框图的基本结构及设计2.1 顺序结构与选择结构2.2 变量与赋值2.3 循环结构§3 几种基本语句3.1 条件语句3.2 循环语句第三章概率§1 随机事件的概率1.1 频率与概率1.2 生活中的概率§2 古典概型2.1 古典概型的特征和概率计算公式2.2 建立概率模型2.3 互斥事件§3模拟方法——概率的应用第一章三角函数§1 周期现象§2 角的概念的推广§3 弧度制§4 正弦函数和余弦函数的定义与诱导公式4.1 任意角的正弦函数、余弦函数的定义 4.2 单位圆与周期性4.3 单位圆与诱导公式§5 余弦函数的性质与图像5.1 从单位圆看正弦函数的性质5.2 正弦函数的图像5.3 正弦函数的性质§6 余弦函数的图像与性质6.1 余弦函数的图像6.2 余弦函数的性质§7 正切函数7.1 正切函数的定义7.2 正切函数的图像和性质7.3 正切函数的诱导公式§8 函数)sin(ϕ+ω=xAy的图像§9 三角函数的简单应用第二章平面向量§1 从位移、速度、力到向量1.1 位移、速度和力1.2 向量的概念§2 从位移的合成到向量的加法2.1 向量的加法2.2 向量的减法§3 从速度的倍数到数乘向量3.1 数乘向量3.2 平面向量基本定理§4 平面向量的坐标4.1 平面向量的坐标表示4.2 平面向量线性运算的坐标表述4.3 向量平行的坐标表示§5 从力做的功到向量的数量积§6 平面向量数量积的坐标表示§7 向量应用举例7.1 点到直线的距离公式7.2 向量的应用举例第三章三角恒等变形§1 同角三角函数的基本关系§2 两角和与差的三角函数2.1 两角差的余弦函数2.2 两角和与差的正弦、余弦函数 2.3 两角和与差的正切函数§3 二倍角的三角函数第一章数列§1 数列1.1 数列的概念1.2 数列的函数特性§2 等差数列2.1 等差数列2.2 等差数列的前n项和§3 等比数列3.1 等比数列3.2 等比数列的前n项和§4 数列在日常经济生活中的应用第二章解三角形§1 正弦定理与余弦定理1.1 正弦定理1.2 余弦定理§2 三角形中的几何计算§3 解三角形的实际应用举例第三章不等式§1 不等关系1.1 不等关系1.2 比较大小§2 一元二次不等式2.1 一元二次不等式的解法2.2 一元二次不等式的应用§3 基本不等式3.1 基本不等式3.2 基本不等式与最大小值§4 简单线性规划4.1 二元一次不等式组与平面区域 4.2 简单线性规划4.3 简单线性规划的应用第一章常用逻辑用语§1 命题§2 充分条件与必要条件2.1 充分条件2.2 必要条件2.3 充要条件§3 全称量词与存在量词3.1 全称量词与全称命题3.2 存在量词与特称命题3.3 全称命题与特称命题的否定§4 逻辑联结词“且”“或”“非”4.1 逻辑联结词“且”4.2 逻辑联结词“或”4.3 逻辑联结词“非”第二章空间向量与立体几何§1 从平面向量到空间向量§2 空间向量的运算§3 向量的坐标表示和空间向量基本定理3.1 空间向量的标准正交分解与坐标表示 3.2 空间向量基本定理3.3 空间向量运算的坐标表示§4 用向量讨论垂直与平行§5 夹角的计算5.1 直线间的夹角5.2 平面间的夹角5.3 直线与平面的夹角§6 距离的计算第三章圆锥曲线与方程§1 椭圆1.1 椭圆及其标准方程1.2 椭圆的简单性质§2 抛物线2.1 抛物线及其标准方程2.2 抛物线的简单性质§3 双曲线3.1 双曲线及其标准方程3.2 双曲线的简单性质§4 曲线与方程4.1 曲线与方程4.2 圆锥曲线的共同特征4.3 直线与圆锥曲线的交点第一章推理与证明§1 归纳与类比1.1 归纳推理1.2 类比推理§2 综合法与分析法2.1 综合法2.2 分析法§3 反证法§4 数学归纳法第二章变化率与导数§1 变化的快慢与变化率§2 导数的概念及其几何意义2.1 导数的概念2.2 导数的几何意义§3 计算导数§4 导数的四则运算法则4.1 导数的加法与减法法则4.2 导数的乘法与除法法则§5 简单复合函数的求导法则第三章导数应用§1 函数的单调性与极值1.1 导数与函数的单调性1.3 函数的极值§2 导数在实际问题中的应用2.1 实际问题中导数的应用2.2 最大值、最小值问题第四章定积分§1 定积分的概念1.1 定积分背景——面积和路程问题 1.2 定积分§2 微积分基本定理§3 定积分的简单应用3.1 平面图形的面积3.2 简单几何体的体积第五章数系的扩充与复数的引入§1 数系的扩充与复数的引入1.1 数的概念的扩展1.2 复数的有关概念§2 复数的四则运算2.1 复数的加法与减法2.2 复数的乘法与除法第一章计数原理§1 分类加法计数原理和分步乘法计数原理1.1 分类加法计数原理1.2 分类乘法计数原理§2 排列§3 组合§4 简单计数问题§5 二项式定理5.1 二项式定理5.2 二项式系数的性质第二章概率§1 离散型随机变量及其分布列§2 超几何分布§3 条件概率与独立事件§4 二项分布§5 离散型随机变量的均值与方差§6 正态分布6.1 连续型随机变量6.2 正态分布第三章统计案例§1 回归分析1.1 回归分析1.2 相关系数1.3 可线性化的回归分析§2 独立性检验2.1 独立性检验2.2 独立性检验的基本思想2.3 独立性检验的应用第一章直线、多边形、圆§1 全等与相似§2 圆与直线§3 圆与四边形第二章圆锥曲线§1 截面欣赏§2 直线与球、平面与球的位置关系§3 柱面与平面的截面§4 平面截圆锥面§5 圆锥曲线的几何性质第一章平面向量与二阶方阵§1平面向量及向量的运算§2向量的坐标表示及直线的向量方程§3二阶方阵与平面向量的乘法第二章几何变换与矩阵§1几种特殊的矩阵变换§2矩阵变换的性质第三章变换的合成与矩阵乘法§1变换的合成与矩阵乘法§2矩阵乘法的性质第四章逆变换与逆矩阵§1逆变换与逆矩阵§2初等变换与逆矩阵§3二阶行列式与逆矩阵§4可逆矩阵与线性方程组第五章矩阵的特征值与特征向量§1矩阵变换的特征值与特征向量§2特征向量在生态模型中的简单应用第一章坐标系§1 平面直角坐标系§2 极坐标系§3 柱坐标系和球坐标系第二章参数方程§1 参数方程的概念§2 直线和圆锥曲线的参数方程§3 参数方程化成普通方程§4 平摆线和渐开线§5 圆锥曲线的几何性质第一章不等关系与基本不等式§1 不等式的性质§2 含有绝对值的不等式§3 平均值不等式§4 不等式的证明§5 不等式的应用第二章几个重要不等式§1 柯西不等式§2 排序不等式§3 数学归纳法与贝努利不等式第一章常用逻辑用语§1 命题§2 充分条件与必要条件2.1 充分条件2.2 必要条件2.3 充要条件§3 全称量词与存在量词3.1 全称量词与全称命题3.2 存在量词与特称命题3.3 全称命题与特称命题的否定§4 逻辑联结词“且”“或”“非”4.1 逻辑联结词“且”4.2 逻辑联结词“或”4.3 逻辑联结词“非”第二章圆锥曲线与方程§1 椭圆1.1 椭圆及其标准方程1.2 椭圆的简单性质§2 抛物线2.1 抛物线及其标准方程2.2 抛物线的简单性质§3 双曲线3.1 双曲线及其标准方程3.2 双曲线的简单性质第三章变化率与导数§1 变化的快慢与变化率§2 导数的概念及其几何意义2.1 导数的概念2.2 导数的几何意义§3 计算导数§4 导数的四则运算法则4.1 导数的加法与减法法则4.2 导数的乘法与除法法则第四章导数应用§1 函数的单调性与极值1.1 导数与函数的单调性1.2 函数的极值§2 导数在实际问题中的应用2.1 实际问题中导数的应用 2.2 最大值、最小值问题第一章统计案例§1 回归分析1.1 回归分析1.2 相关系数1.3 可线性化的回归分析§2 独立性检验2.1 条件概率与独立事件2.2 独立性检验2.3 独立性检验的基本思想2.4 独立性检验的应用第二章框图§1 流程图§2 结构图第三章推理与证明§1 归纳与类比1.1 归纳推理1.2 类比推理§2 数学证明§3 综合法与分析法3.1 综合法3.2 分析法§4 反证法第四章数系的扩充与复数的引入§1 数系的扩充与复数的引入1.1 数的概念的扩展1.2 复数的有关概念§2 复数的四则运算2.1 复数的加法与减法2.2 复数的乘法与除法。

数学：第一章《立体几何初步》学案（新人教版B 版必修2）第一章《立体几何初步》单元小结导航知识链接点击考点（1）了解柱，锥，台，球及简单组合体的结构特征。

（2） 能画出简单空间图形的三视图，能识别三视图所表示的立体模型，并会用斜二测法画出它们的直观图。

（3） 通过观察用平行投影与中心投影这两种方法画出的视图与直观图，了解空间图形的不同表示形式。

（4） 理解柱，锥，台，球的表面积及体积公式。

（5） 理解平面的基本性质及确定平面的条件。

（6） 掌握空间直线与直线，直线与平面，平面与平面平行的判定及性质。

（7） 掌握空间直线与平面，平面与平面垂直的判定及性质。

名师导航1.学习方法指导 （1） 空间几何体①空间图形直观描述了空间形体的特征，我们一般用斜二测画法来画空间图形的直观图。

②空间图形可以看作点的集合，用符号语言表述点，线，面的位置关系时，经常用到集合的有关符号，要注意文字语言，符号语言，图形语言的相互转化。

③柱，锥，台，球是简单的几何体，同学们可用列表的方法对它们的定义，性质，表面积及体积进行归纳整理。

④对于一个正棱台，当上底面扩展为下底面的全等形时，就变为一个直棱柱；当上底面收缩为中心点时，就变为一个正棱锥。

由1()2S c c h ''=+正棱台侧和()3hV s s '=正棱台，就可看出它们的侧面积与体积公式的联系。

（2） 点，线，面之间的位置关系①“确定平面”是将空间图形问题转化为平面图形问题来解决的重要条件，这种转化最基本的就是三个公理。

②空间中平行关系之间的转化：直线与直线平行 直线与平面平行平面与平面平行。

③空间中垂直关系之间的转化：直线与直线垂直 直线与平面垂直平面与平面垂直。

2.思想方法小结在本章中需要用到的数学思想方法有：观察法，数形结合思想，化归与转化思想等。

主要是立体几何问题转化为平面几何问题，平行与垂直的相互转化等。

3.综合例题分析例1：如图，P 是∆ABC 所在平面外一点，A '，B '，C '分别是PBC ∆，PCA ∆，PAB ∆的重心。

立体几何一、空间位置关系的证明(一)平行关系的证明1．线面平行的判定定理和性质定理2.面面平行的判定定理和性质定理3.重要结论(1)垂直于同一条直线的两个平面平行，即若a⊥α，a⊥β，则α∥β；(2)垂直于同一个平面的两条直线平行，即若a⊥α，b⊥α，则a∥b；(3)平行于同一个平面的两个平面平行，即若α∥β，β∥γ，则α∥γ.(4)几何体中线面平行的证明常利用平行四边形的定义、性质或三角形中位线(二)垂直关系的证明1．直线与平面垂直(1)定义：:如果直线l与平面α内的任意一条直线都垂直，则直线l与平面α垂直．(2)判定定理与性质定理2.直线和平面所成的角(1)定义：平面的一条斜线和它在平面上的射影所成的锐角，叫做这条直线和这个平面所成的角．若一条直线垂直于平面，它们所成的角是直角，若一条直线和平面平行，或在平面内，它们所成的角是0°的角． (2)范围：[0，π2]． 3．平面与平面垂直 (1)二面角的有关概念①二面角：从一条直线出发的两个半平面所组成的图形叫做二面角；②二面角的平面角：在二面角的棱上任取一点，以该点为垂足，在两个半平面内分别作垂直于棱的两条射线，这两条射线所构成的角叫做二面角的平面角． (2)平面和平面垂直的定义两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直．(3)平面与平面垂直的判定定理与性质定理4.重要结论(1)若两平行线中的一条垂直于一个平面，则另一条也垂直于这个平面． (2)若一条直线垂直于一个平面，则它垂直于这个平面内的任何一条直线(证明线线垂直的一个重要方法)．(3)垂直于同一条直线的两个平面平行．(4)一条直线垂直于两平行平面中的一个，则这一条直线与另一个平面也垂直． (5)在几何体中垂直关系的证明中要重视勾股定理及平面几何知识的应用，如：菱形的对角线互相垂直，等腰三角形底边上的中线垂直于底边等。

二、立体几何中的向量方法 (一)证明平行与垂直1．直线的方向向量与平面的法向量的确定(1)直线的方向向量：在直线上任取一非零向量作为它的方向向量．(2)平面的法向量可利用方程组求出：设a ，b 是平面α内两不共线向量，n 为平面α的法向量，则求法向量的方程组为⎩⎪⎨⎪⎧n ·a ＝0，n ·b ＝0.2．用向量证明空间中的平行关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2，则l 1∥l 2(或l 1与l 2重合)⇔v 1∥v 2. (2)设直线l 的方向向量为v ，与平面α共面的两个不共线向量v 1和v 2，则l ∥α或l ⊂α⇔存在两个实数x ，y ，使v ＝x v 1＋y v 2.(3)设直线l 的方向向量为v ，平面α的法向量为u ，则l ∥α或l ⊂α⇔v ⊥u . (4)设平面α和β的法向量分别为u 1，u 2，则α∥β⇔u 1∥u 2. 3．用向量证明空间中的垂直关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2，则l 1⊥l 2⇔v 1⊥v 2⇔v 1·v 2＝0. (2)设直线l 的方向向量为v ，平面α的法向量为u ，则l ⊥α⇔v ∥u . (3)设平面α和β的法向量分别为u 1和u 2，则α⊥β⇔u 1⊥u 2⇔u 1·u 2＝0. （二）求空间角1．两条异面直线所成角的求法设a ，b 分别是两异面直线l 1，l 2的方向向量，则2.直线与平面所成角的求法设直线l 的方向向量为a ，平面α的法向量为n ，直线l 与平面α所成的角为θ，a 与n 的夹角为β，则sin θ＝|cos β|＝|a ·n ||a ||n |.3．求二面角的大小(1)如图①，AB ，CD 分别是二面角α－l －β的两个面内与棱l 垂直的直线，则二面角的大小θ＝〈AB→，CD →〉．(2)如图②③，n 1，n 2分别是二面角α－l －β的两个半平面α，β的法向量，则二面角的大小θ满足|cos θ|＝|cos 〈n 1，n 2〉|，二面角的平面角大小是向量n 1与n 2的夹角(或其补角)．。

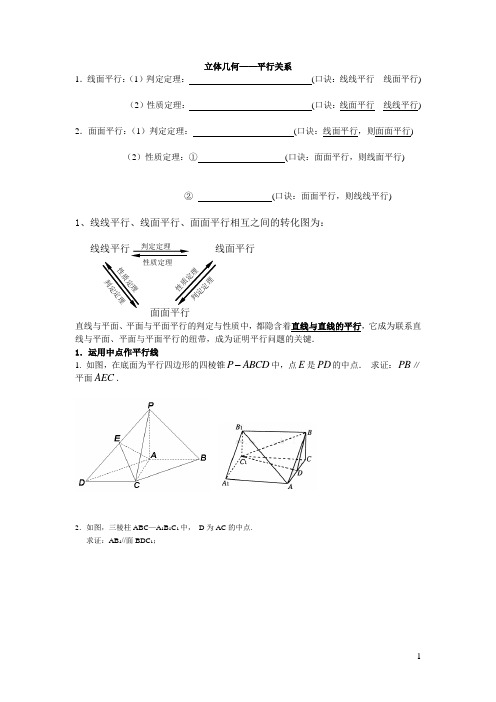
立体几何——平行关系1．线面平行：（1）判定定理： (口诀：线线平行 线面平行)（2）性质定理： (口诀：线面平行 线线平行)2．面面平行：（1）判定定理： (口诀：线面平行，则面面平行)（2）性质定理：① (口诀：面面平行，则线面平行)② (口诀：面面平行，则线线平行)1、线线平行、线面平行、面面平行相互之间的转化图为：线线平行 线面平行面面平行直线与平面、平面与平面平行的判定与性质中，都隐含着直线与直线的平行，它成为联系直线与平面、平面与平面平行的纽带，成为证明平行问题的关键． 1．运用中点作平行线1. 如图，在底面为平行四边形的四棱锥P ABCD 中，点E 是PD 的中点． 求证：PB ∥平面AEC ．2．如图，三棱柱ABC —A 1B 1C 1中， D 为AC 的中点. 求证：AB 1//面BDC 1；判定定理 性质定理性质定理 判定定理判定定理性质定理PEDCBA3．已知四棱锥P ABCD 的底面是距形，Ｍ、Ｎ分别是ＡＤ、ＰＢ的中点，求证ＭＮ∥平面PCD ．4如图，四棱锥P －ABCD 的底面是平行四边形，点E 、F 分别为棱AB 、 PD 的中点．求证：AF ∥平面PCE ；5．正方体ABCD —A 1B 1C 1D 1中O 为正方形ABCD 的中心，M 为BB 1的中点， 求证： D 1O//平面A 1BC 1;6、在四棱锥P-ABCD 中，AB ∥CD ，AB=21DC ，中点为PD E . 求证：AE ∥平面PBC ；2．运用比例作平行线1、如图：S 是平行四边形ABCD 平面外一点，M 、N 分别是SA 、BD 上的点，且SM AM =NDBN， 求证：MN ∥平面SDC2.如图所示，正四棱锥P —ABCD 的各棱长均为13，M ，N 分别为PA ，BD 上的点，且PM ∶MA =BN ∶ND =5∶8. （1）求证：直线MN ∥平面PBC ； （2）求线段MN 的长.A CNP D M BG图1EFBACDP3．P 是△ABC 所在平面外一点，A ′、B ′、C ′分别是△PBC 、△PCA 、△PAB 的重心。

2018年9月使用的高中数学新教材目录及框架今年（2018年）9月将实施新的高中数学课程标准（2017版），课程标准由国家教材委员会统一修订，不再分各种版本，教材变了，怎么变，大家抢先看：必修（第一册）（共计72课时）第一章集合与常用逻辑用语（10课时）第二章一元二次函数、方程和不等式(8课时)第三章函数概念与性质（12课时）第四章指数函数与对数函数（16课时）第五章三角函数（23课时）必修（第二册）（共计69课时）第六章平面向量及其应用（18课时）第七章复数（8课时）第八章立体几何初步（19课时）第九章统计（13课时）第十章概率（9课时）选择性必修（第一册）（共计43课时）第一章空间向量与立体几何（15课时）第二章直线和圆的方程（16课时）第三章圆锥曲线的方程（12课时）选择性必修（第二册）（共计30课时）第四章数列（14课时）第五章一元函数的导数及其应用（16课时）选择性必修（第三册）（共计35课时）第六章计数原理（11课时）第七章随机变量及其分布（10课时）第八章成对数据的统计分析（9课时）具体的章节必修（第一册）（共计72课时）第一章集合与常用逻辑用语（10课时）1.1集合的概念1.2集合间的基本关系1.3集合的基本运算阅读与思考集合中元素的个数1.4充分条件与必要条件1.5全称量词与存在量词阅读与思考命题及其关系第二章一元二次函数、方程和不等式(8课时) 2.1等式性质与不等式性质2.2基本不等式2.3二次函数与一元二次方程、不等式第三章函数概念与性质（12课时）3.1函数的概念及其表示阅读与思考函数概念的发展历程3.2函数的基本性质信息技术应用用计算机绘制函数图象3.3幂函数探究与发现探究函数1=+的图象与性质y xx3.4函数的应用（一）文献阅读与数学写作* 函数的形成与发展第四章指数函数与对数函数（16课时）4.1指数4.2指数函数阅读与思考放射性物质的衰减信息技术应用探究指数函数的性质4.3对数阅读与思考对数的发明4.4对数函数探究与发现互为反函数的两个函数图象间的关系4.5函数的应用（二）阅读与思考中外历史上的方程求解文献阅读与数学写作* 对数概念的形成和发展数学建模（3）建立函数模型解决实际问题第五章三角函数（23课时）5.1任意角和弧度制5.2三角函数的概念阅读与思考 三角学与天文学5.3诱导公式5.4三角函数的图象与性质探究与发现 函数sin()y A x ωϕ=+ 及函数cos()y A x ωϕ=+的周期 探究与发现 利用单位圆的性质研究正弦函数、余弦函数的性质5.5三角恒等变换信息技术应用 利用信息技术制作三角函数表5.6函数sin()y A x ωϕ=+的图象和性质5.7三角函数的应用阅读与思考 振幅、周期、频率、相位必修（第二册）（共计69课时）第六章 平面向量 及 其 应 用（18课时）6.1平面向量的概念阅读与思考 向量及向量符号的由来6.2平面向量的运算6.3平面向量基本定理及坐标表示6.4平面向量的应用阅读与思考 海伦和秦久韶数学探究（2）用向量法研究三角形的性质第七章复数（8课时）7.1复数的概念7.2复数的四则运算阅读与思考代数基本定理7.3* 复数的三角表示探究与发现1的n次方根第八章立体几何初步（19课时）8.1基本立体图形8.2立体图形的直观图阅读与思考画法几何与蒙日8.3简单几何体的表面积与体积探究与发现祖暅原理与柱体、锥体的体积8.4空间点、直线、平面之间的位置关系8.5空间直线、平面的平行8.6空间直线、平面的垂直阅读与思考欧几里得《原本》与公理化方法文献阅读与数学写作* 几何学的发展第九章统计（13课时）9.1 随机抽样阅读与思考如何得到敏感性问题的诚实反应信息技术应用统计软件的应用9.2用样本估计总体阅读与思考统计学在军事中的应用——二战时德国坦克总量的估计问题阅读与思考大数据9.3统计分析案例公司员工的肥胖情况调查分析第十章概率（9课时）10.1 随机事件与概率10.2事件的相互独立性10.3频率与概率阅读与思考孟德尔遗传规律选择性必修（第一册）（共计43课时）第一章空间向量与立体几何（15课时）1.1空间向量及其运算1.2空间向量基本定理1.3空间向量及其运算的坐标表示阅读与思考向量概念的推广与应用1.4空间向量的应用第二章直线和圆的方程（16课时）2.1直线的倾斜角与斜率2.2直线的方程阅读与思考方向向量与直线的参数方程2.3直线的交点坐标与距离公式阅读与思考笛卡儿与解析几何2.4圆的方程阅读与思考 坐标法与数学机械化2.5直线与圆、圆与圆的位置关系第三章 圆锥曲线的方程（12课时）3.1椭圆信息技术应用 用信息技术工具探究点的轨迹：椭圆3.2双曲线阅读与思考 为什么b y x a=±是双曲线22221x y a b -=的渐近线 3.3抛物线阅读与思考 为什么二次函数2(0)y ax bx c a =++≠的图象是抛物线 阅读与思考 圆锥曲线的光学性质及其应用文献阅读与数学写作* 解析几何的形成与发展 选择性必修（第二册）（共计30课时）第四章 数 列（14课时）4.1数列的概念阅读与思考 斐波那契数列4.2等差数列4.3等比数列阅读与思考 中国古代数学家求数列和的方法4.4数学归纳法*第五章 一元函数的导数及其应用（16课时）5.1导数的概念及其意义5.2导数的运算探究与发现牛顿法——用导数方法求方程的近似解5.3导数在研究函数中的应用信息技术应用图形技术与函数性质文献阅读与数学写作* 微积分的创立与发展选择性必修（第三册）（共计35课时）第六章计数原理（11课时）6.1分类加法计数原理与分步乘法计数原理探究与发现子集的个数有多少6.2排列与组合探究与发现组合数的两个性质6.3二项式定理数学探究（2）杨辉三角的性质与应用第七章随机变量及其分布（10课时）7.1条件概率与全概率公式阅读与思考换还是不换？7.2离散型随机变量及其分布列7.3离散型随机变量的数字特征7.4二项分布与超几何分布探究与发现二项分布的性质7．5 正态分布信息技术应用概率分布图及概率计算第八章成对数据的统计分析（9课时）8.1成对数据的相关关系8.2一元线性回归模型及其应用8.3分类变量与列联表数学建模（3）建立统计模型进行预测。

专题5线面平行与面面平行解答题秒杀秘籍：第一讲线面平行构造之平行四边形法要证明一直线平行于另一平面，可以构造一个平行四边形，利用另一组对边平行且相等来证明这组对边平行．这个另一组对边，往往在重垂线、水平线、侧平线中寻找，因为它们必然平行，只需要证明相等即可．构造方式：1．重垂线构造法2．水平线构造法3．侧平线构造法【例1】如下图，两个全等的正方形ABCD 和ABFE 所在平面相交于AB ，AC M ∈，EB N ∈且EN AM =，求证：//MN 平面BCF ．【证明】如图，作MG ∥AB 交BC 于G ，作NH ∥AB 交BF 于H ；∵MG ∥AB ，AB ∥NH ，∴MG ∥NH又∵ABCD 和ABFE 是两个全等的正方形∴AC =BE ∠ACB =∠ACB=45°∠MGC =∠NHB =90°∵AM =EN ，∴MC =BNMCG NBH ∴≅△△MG NH ∴=MGHN ∴是平行四边形，∴MN ∥GH∵GH CBF ⊂∴MN ∥平面BCF ．点评：重垂线构造法，因为M 、N 两点都能作重垂线的平行线．【例2】如图，在四棱锥ABCD S -中，已知底面ABCD 为直角梯形，其中BC AD //，︒=∠90BAD ，⊥SA 底面ABCD ，2===BC AB SA ．32tan =∠SDA ．（1）求四棱锥ABCD S -的体积；（2）在棱SD 上找一点E ，使//CE 平面SAB ，并证明．【解析】（1）∵SA ⊥底面ABCD ，tan ∠SDA ＝23，SA ＝2，∴AD ＝3．由题意知四棱锥S －ABCD 的底面为直角梯形，且SA ＝AB ＝BC ＝2，V S －ABCD ＝13×SA ×12×(BC ＋AD )×AB ＝13×2×12×(2＋3)×2＝103．（2）当点E 位于棱SD 上靠近D 的三等分点处时，可使CE ∥平面SAB ．取SD 上靠近D 的三等分点为E ，取SA 上靠近点A 的三等分点为F ，连接CE ，EF ，BF ，则EF =23AD ，BC =23AD ，∴BC=EF ．∴CE ∥BF ．又∵BF ⊂平面SAB ，CE ⊄平面SAB ，∴CE ∥平面SAB ．【例3】如图所示，在直四棱柱1111D C B A ABCD -中，已知AB AD DD DC 221===，AD ⊥DC ，AB ∥DC ，设E 是DC 的中点．求证：E D1∥平面BD A 1．【证明】如图，连接BE ，则四边形DABE 为正方形，∴11D A AD BE ==，且11////D A AD BE ，∴四边形EB D A 11为平行四边形，∴BA E D 11//又⊄E D 1平面BD A 1，⊄B A 1平面BDA 1∴E D 1∥平面BD A 1．点评：侧平线构造法，A 1、D 1位于侧平线两端．秒杀秘籍：第二讲线面平行构造之三角形中位线法证明一直线平行于另一平面，可以找到由一个公共顶点引出的两条线段，并分别找到线段中点，构造三角形中位线来证明线面平行．往往需要找出五点，即两个线段端点，一个中点，公共顶点，再找出另一个中点，最后连线即得．中位线法不需要依托重垂线、水平线、侧平线的载体，但一定要找到公共顶点．【例4】如图，在正方体1111ABCD A B C D -中，E 是1AA 的中点．求证：//1C A 平面BDE ．【证明】设O BD AC = ，∵E 、O 分别是1AA 、AC 的中点，∴EOC A //1又⊄C A 1平面BDE ，⊂EO 平面BDE ，∴//1C A 平面BDE【例5】如图，在正四棱锥P ABCD -中，PA AB a ==,点E 在棱PC 上．问点E 在何处时，//PA EBD 平面，并加以证明．【解析】当E 为PC 中点时，//PA EBD 平面．连接AC ，且AC BD O = ，由于四边形ABCD 为正方形，∴O 为AC 的中点，又E 为中点，∴OE 为△ACP 的中位线，∴EO PA //，又PA ⊄平面EBD ，∴//PA 平面EBD ．【例6】如图，在正三棱柱ABC －A 1B 1C 1中，点D 为棱AB 的中点，BC ＝1，AA 1＝3．（1）求证：BC 1∥平面A 1CD ；（2）求三棱锥D －A 1B 1C 的体积．【解析】（1）证明：连接AC 1交A 1C 于点O ，连接OD ．∵▱ACC 1A 1中，O 为AC 1的中点，D 为AB 的中点，∴OD ∥BC 1，又BC 1⊄平面A 1CD ，OD ⊂平面A 1CD ，∴BC 1∥平面A 1CD ．（2）在正三角形ABC 中，D 为AB 的中点，则CD ⊥AB ，又∵平面ABC ⊥平面ABB 1A 1，∴CD ⊥平面ABB 1A 1．∴CD 为三棱锥D －A 1B 1C 的高，∵CD ＝32，111D B A S △＝32，∴41311111111=⋅==--D B A D B A C C B A D S CD V V △．达标训练1．（2018•江苏）在平行六面体1111ABCD A B C D -中，1AA AB =，111AB B C ⊥．求证：//AB 平面11A B C ；2．（2018•新课标Ⅲ）如图，矩形ABCD 所在平面与半圆弧 CD所在平面垂直，M 是 CD 上异于C ，D 的点．在线段AM 上是否存在点P ，使得//MC 平面PBD ？说明理由．3．（2018•北京）如图，在四棱锥P ABCD -中，底面ABCD 为矩形，平面PAD ⊥平面ABCD ，PA PD ⊥，PA PD =，E ，F 分别为AD ，PB 的中点．求证：//EF 平面PCD ．4．（2017•山东）由四棱柱1111ABCD A B C D -截去三棱锥111C B CD -后得到的几何体如图所示，四边形ABCD 为正方形，O 为AC 与BD 的交点，E 为AD 的中点，1A E ⊥平面ABCD ，证明：1//A O 平面11B CD ．5．（2016•江苏）如图，在直三棱柱111ABC A B C -中，D ，E 分别为AB ，BC 的中点，点F 在侧棱1B B 上，且11B D A F ⊥，1111A C A B ⊥．求证：直线//DE 平面11A C F ．6．（2016•四川）如图，在四棱锥P ABCD -中，PA CD ⊥，//AD BC ，90ADC PAB ∠=∠=︒，12BC CD AD ==．在平面PAD 内找一点M ，使得直线//CM 平面PAB ，并说明理由．7．（2015•天津）如图，已知1AA ⊥平面ABC ，11//BB AA ，3AB AC ==，25BC =，17AA =，127BB =，点E 和F 分别为BC 和1A C 的中点．求证：//EF 平面11A B BA ．8．（2015•山东）如图，三棱台DEF ABC -中，2AB DE =，G ，H 分别为AC ，BC 的中点．求证：//BD 平面FGH ．9．（2014•江苏）如图，在三棱锥P ABC -中，D ，E ，F 分别为棱PC ，AC ，AB 的中点，已知PA AC ⊥，6PA =，8BC =，5DF =．求证：直线//PA 平面DEF ．10．（2014•山东）如图，四棱锥P ABCD -中，AP ⊥平面PCD ，//AD BC ，12AB BC AD ==，E ，F 分别为线段AD ，PC 的中点．求证：//AP 平面BEF ．11．（2014•安徽）如图，四棱锥P ABCD -的底面是边长为8的正方形，四条侧棱长均为217，点G ，E ，F ，H 分别是棱PB ，AB ，CD ，PC 上共面的四点，平面GEFH ⊥平面ABCD ，//BC 平面GEFH ．（1）证明：//GH EF ；（2）若2EB =，求四边形GEFH 的面积．12．（2015•江苏）如图，在直三棱柱111ABC A B C -中，已知AC BC ⊥，1BC CC =，设1AB 的中点为D ，11B C BC E ⋂=．求证：//DE 平面11AA C C ．13．（2013•新课标Ⅱ）如图，直三棱柱111ABC A B C -中，D ，E 分别是AB ，1BB 的中点．（1）证明：1//BC 平面1A CD ；（2）12AA AC CB ===，22AB =，求三棱锥1C A DE -的体积．。

高中数学目录必修一第一章1.1 会合与会合的表示方法1.1.1 会合的观点1.1.2 会合的表示方法第二章2.1 函数2.1.1 函数2.1.2 函数的表示方法2.1.3 函数的单一性2.1.4 函数的奇偶性2.1.5 用计算机作函数图像（选学）2.2 一次函数和二次函数2.2.1 一次函数的性质与图像2.2.2 二次函数的性质与图像2.3 函数的应用（ 1）2.4 函数与方程2.4.1 函数的零点2.4.2 求函数零点近似解的一种计算方法----二分法第三章基本初等函数（1）3.1 指数与指数函数3.1.1 实数指数幂及其运算3.1.2 指数函数3.2 对数与对数函数3.2.1 对数及其运算3.2.2 对数函数3.2.3 指数函数与对数函数的关系3.3 幂函数3.4 函数的应用（ 2）必修二第一章立体几何初步1.1 空间几何体1.1.1 组成空间几何体的基本元素1.1.2 棱柱棱锥棱台的构造特点1.1.3 圆柱圆锥圆台和球1.1.4 投影与直观图1.1.5 三视图1.1.6 棱柱棱锥棱台和球的表面积1.1.7 柱锥台和球的体积1.2 点线面之间的地点关系1.2.1 平面的基天性质与推论1.2.2 空间中的平行关系1.2.3 空间中的垂直关系第二章平面分析几何初步2.1 平面直角坐标系中的基本公式2.1.1 数轴上的基本公式2.1.2 平面直角坐标系中的基本公式2.2 直线的方程2.2.1 直线方程的观点与直线的斜率2.2.2 直线方程的集中形式2.2.3 两条直线的地点关系2.2.4 点到直线的距离2.3 圆的方程2.3.1 圆的标准方程2.3.2 圆的一般方程2.3.3 直线与圆的地点关系2.3.4 圆与圆的地点关系2.4 空间直角坐标系2.4.1 空间直角坐标系2.4.2 空间两点距离公式必修三第一章算法初步1.1 算法与程序框图1.1.1 算法的观点1.1.2 程序框图1.1.3 算法的三种基本逻辑构造和框图表示1.2 基本算法语句1.2.1 赋值输入输出语句1.2.2 条件语句1.2.3 循环语句1.3 中国古代数学中的算法事例第二章统计2.1 随机抽样2.1.1 简单的随机抽样2.1.2 系统抽样2.1.3 分层抽样2.1.4 数据的采集2.2 用样本预计整体2.2.1 用样本的频次散布预计整体的散布2.2.2 用样本的数字特点预计整体的数字特点2.3 变量的有关性2.3.1 变量间的互相关系2.3.2 两个变量的线性有关第三章概率3.1 事件与概率3.1.1 随机现象3.1.2 事件与基本领件空间3.1.3 频次与概率3.1.4 概率的加法公式3.2 古典概型3.2.1 古典概型3.2.2 概率的一般加法公式（选学）3.3 随机数的含义与应用3.3.1 几何概型3.3.2 随机数的含义与应用3.4 概率的应用必修四第一章基本的初等函数（2）1.1 随意角的观点与弧度制1.1.1 角的观点的推行1.1.2 弧度制和弧度制与角度制的换算1.2 随意角的三角函数1.2.1 三角函数的定义1.2.2 单位圆与三角函数线1.2.3 同角三角函数的基本关系式1.2.4 引诱公式1.3 三角函数的图像与性质1.3.1 正弦函数的图像与性质1.3.2 余弦函数正切函数的图像与性质1.3.3 已知三角函数值求角第二章平面向量2.1 向量的线性运算2.1.1 向量的观点2.1.2 向量的加法2.1.3 向量的减法2.1.4 数乘向量2.1.5 向量共线的条件和轴上向量坐标运算2.2 向量的分解和向量的坐标运算2.2.1 平面向量基本定理2.2.2 向量的正交分解与向量的直角坐标运算2.2.3 用平面向量坐标表示向量共线条件2.3 平面向量的数目积2.3.1 向量数目积的物理背景与定义2.3.2 向量数目积的运算律2.3.3 向量数目积的坐标运算与胸怀公式2.4 向量的应用2.4.1 向量在几何中的应用2.4.2 向量在物理中的应用第三章三角恒等变换3.1 和角公式3.1.1 两角和与差的余弦3.1.2 两角和与差的正弦3.1.3 两角和与差的正切3.2 倍角公式和半角公式3.2.1 倍角公式3.2.2 半角的正弦余弦和正切3.3 三角函数的积化和差与和差化积必修五第一章解三角形1.1 正弦定理和余弦定理1.1.1 正弦定理1.1.2 余弦定理1.2 应用举例第二章数列2.1 数列2.1.1 数列2.1.2 数列的递推公式（选学）2.2 等差数列2.2.1 等差数列2.2.2 等差数列的前n 项和2.3 等比数列2.3.1 等比数列2.3.2 等比数列的前n 项和第三章不等式3.1 不等关系与不等式3.1.1 不等关系与不等式3.1.2 不等式性质3.2 均值不等式3.3 一元二次不等式及其解法3.4 不等式的实质应用3.5 二元一次不等式（组）与简单的线性规划问题3.5.1 二元一次不等式（组）所表示的平面地区3.5.2 简单线性规划选修 2-1第一章常用逻辑用语1.1 命题与量词1.1.1 命题1.1.2 量词1.2 基本逻辑联络词1.2.1 且与或1.2.2 非（否认）1.3 充足条件必需条件与命题的四种形式1.3.1 推出与充足条件必需条件1.3.2 命题的四种形式第二章圆锥曲线方程2.1 曲线方程2.1.1 曲线与方程的观点2.1.2 由曲线求它的方程由方程研究曲线性质2.2 椭圆2.2.1 椭圆的标准方程2.2.2 椭圆的几何性质2.3 双曲线2.3.1 双曲线的标准方程2.3.2 双曲线的几何性质2.4 抛物线2.4.1 抛物线的标准方程2.4.2 抛物线的几何性质2.5 直线与圆锥曲线第三章空间向量与几何体3.1 空间向量及其运算3.1.1 空间向量的线性运算3.1.2 空间向量的基本定理3.1.3 两个向量的数目积3.1.4 空间向量的直角坐标运算3.2 空间向量在立体几何中的应用3.2.1 直线的方向向量与直线的向量方程3.2.2 平面的法向量与平面的向量表示3.2.3 直线与平面的夹角3.2.4 二面角及其胸怀3.2.5 距离（选学）选修 2-2第一章导数及其应用1.1 导数1.1.1 函数的均匀变化率1.1.2 刹时速度与导数1.1.3 导数的几何1.2 导数的运算1.2.1 常数函数与幂函数的导数1.2.2 导数公式表及数学软件的应用1.2.3 导数的四则运算法例1.3 导数的应用1.3.1 利用导数判断函数的单一性1.3.2 利用导数研究函数的极值1.3.3 导数的实质应用1.4 定积分与微积分的基本定理1.4.1 曲边梯形面积与定积分1.4.2 微积分基本定理第二章推理与证明2.1 合情推理与演绎推理2.1.1 合情推理2.1.2 演绎推理2.2 直接证明与间接证明2.2.1 综合法与剖析法2.2.2 反证法2.3 数学概括法2.3.1 数学概括法2.3.2 数学概括法应用举例第三章数系的扩大与复数3.1 数系的扩大与复数的观点3.1.1 实数系3.1.2 复数的观点3.1.3 复数的几何意义3.2 复数的运算3.2.1 复数的加法与减法3.2.2 复数的乘法3.2.3 复数的除法选修 2-3第一章计数原理1.1 基本计数原理1.2 摆列与组合1.2.1 摆列1.2.2 组合1.3 二项式定理1.3.1 二项式定理1.3.2 杨辉三角第二章概率2.1 失散型随机变量及其散布列2.1.1 失散型随机变量2.1.2 失散型随机变量的散布列2.1.3 超几何散布2.2 条件概率与实践的独立性2.2.1 条件概率2.2.2 事件的独立性2.2.3 独立重复试验与二项散布2.3 随机变量的数字特点2.3.1 失散型随机变量的数学希望2.3.2 失散型随机变量的方差2.4 正态散布第三章统计事例3.1 独立性查验3.2 回归剖析选修 4-4第一章坐标系1.1 直角坐标系平面上的伸缩变换1.1.1 直角坐标系1.1.2 平面上的伸缩变换1.2 极坐标系1.2.1 平面上点的极坐标1.2.2 极坐标与直角坐标的关系1.3 曲线的极坐标方程1.4 圆的极坐标方程1.4.1 圆心在极轴上且过极点的圆1.4.2 圆心在点（ a，∏ /2 ）处且过极点的圆1.5 柱坐标系和球坐标系1.5.1 柱坐标系1.5.2 球坐标系第二章参数方程2.1 曲线的参数方程2.1.1 抛射体的运动2.1.2 曲线的参数方程2.2 直线与圆的参数方程2.2.1 直线的参数方程2.2.2 圆的参数方程2.3 圆锥曲线的参数方程2.3.1 椭圆的参数方程2.3.2 双曲线的参数方程2.3.3 抛物线的参数方程2.4 一些常有曲线的参数方程2.4.1 摆线的参数方程2.4.2 圆的渐开线的参数方程。

高中数学目录必修一第一章集合§1 集合的含义与表示§2 集合的基本关系§3 集合的基本运算3.1交集与全集3.2全集与补集阅读材料第二章函数§1 生活中的变量关系§2 对函数的进一步认识2.1函数概念2.2函数的表示法2.3映射阅读材料生活中的映射§3 函数的单调性§4 二次函数的再研究4.1二次函数的图像4.2二次函数的性质§5 简单的幂函数阅读材料函数概念的发展——从解析式到对应关系课题学习个人所得税的计算第三章指数函数和对数函数§1 正整数指数函数§2 指数扩充及其运算性质2.1指数概念的扩充2.2指数运算的性质§3 指数函数3.1指数函数的概念3.2指数函数y=2x和y=（）x的图像和性质3.3指数函数的图像和性质§4 对数4.1对数及其运算4.2换底公式§5 对数函数5.1对数函数的概念5.2 y=log2x的图像和性质5.3对数函数的图像和性质§6 指数函数、幂函数、对数函数增长的比较阅读材料历史上数学计算方面的三大发明第四章函数应用§1 函数与方程1.1利用函数性质判定方程解的存在1.2利用二分法求方程的近似解§2 实际问题的函数建模2.1实际问题的函数刻画2.2用函数模型解决实际问题2.3函数建模案例阅读材料函数与中学数学探究活动同种商品不同型号的价格问题必修二第一章立体几何初步1.简单几何体1.1简单旋转体1.2简单多面体2.直观图3.三视图3.1简单组合体的三视图3.2由三视图还原成实物图4.空间图形的基本关系与公理4.1空间图形基本关系的认识4.2空间图形的公理5.平行关系5.1平行关系的判定5.2平行关系的性质6.垂直关系6.1垂直关系的判定6.2垂直关系的性质7.简单几何体的面积和体积7.1简单几何体的侧面积7.2棱柱、棱锥、棱台和圆柱、圆锥、圆台的体积7.3球的表面积和体积阅读材料蜜蜂是对的课题学习正方体截面的形状第二章解析几何初步1.直线与直线的方程1.1直线的倾斜角和斜率1.2直线的方程1.3两条直线的位置关系1.4两条直线的交点1.5平面直角坐标系中的距离公式2.圆与圆的方程2.1圆的标准方程2.2圆的一般方程2.3直线与圆、圆与圆的位置关系3.空间直角坐标系3.1空间直角坐标系的建空间直角坐标系中点3.3空间两点间的距离公式阅读材料笛卡尔与解析几何探究活动1 打包问题探究活动2 追及问题必修三第一章统计1.从普查到抽样阅读材料选举的预测2.抽样方法2.1简单随机抽样2.2分层抽样与系统抽样3.统计图表4.数据的数字特征4.1平均数、中位数、众数、极差、方差4.2标准差5.用样本估计总体5.1估计总体的分布5.2估计总体的数字特征阅读材料标准差的用途6.统计活动：结婚年龄的变化7.相关性8.最小二乘估计阅读材料统计小史课题学习调查通俗歌曲的流行趋势第二章算法初步1.算法的基本思想1.1算法案例分析1.2排序问题与算法的多样性阅读材料物不知数2.算法框图的基本结构及设计2.1顺序结构与选择结构2.2变量与赋值2.3循环结构阅读材料美索不达米亚人的开方算法3.几种基本语句3.1条件语句3.2循环语句阅读材料算法的复杂性课题学习确定线段n等分点的算法第三章概率1.随机事件的概率1.1频率与概率1.2生活中的概率2.古典概型2.1古典概型的特征和概率计算公式2.2建立概率模型2.3互斥事件3.模拟方法——概率的应用探究活动用模拟方法估计圆周率π的值附录1 4000以下的素数表附录2上机实现参考程序必修四第一章三角函数1.周期现象2.角的概念与推广3.弧度制4.正弦函数和余弦函数的定义与诱导公式4.1任意角的正弦函数、余弦函数的定义4.2单位圆与周期性4.3单位圆与诱导公式5.正弦函数的性质与图像5.1从单位圆看正弦函数的性质5.2正弦函数的图像5.3正弦函数的性质6.余弦函数的图像和性质6.1余弦函数的图像6.2余弦函数性质7.正切函数7.1正切函数定义7.2正切函数的图像与性质7.3正切函数的诱导公式8.函数y=A sin(ωx+ψ)的图像9.三角函数的简单应用阅读材料数学与音乐课题学习利用现代信息技术探究y=A sin(ωx+ψ)（A＞0，ω＞0）的图像第二章平面向量1.从位移、速度、力到向量1.1位移、速度和力1.2向量的概念2.从位移的合成到向量的加法2.1向量的加法2.2向量的减法3.从速度的倍数到数乘向量3.1数乘向量3.2平面向量基本定理4.平面向量的坐标4.1平面向量的坐标表示4.2平面向量线性运算的坐标表示4.3向量平行的坐标表示5.从力做的功到向量的数量积6.平面向量数量积的坐标表示7.向量应用举例7.1点到直线的距离公式7.2向量的应用举例阅读材料向量与中学数学第三章三角恒等变形1.同角三角函数的基本关系2.两角和与差的三角函数2.1两角差的余弦函数2.2两角和与差的正弦、余弦函数2.3两角和与差的正切函数3.二倍角的三角函数阅读材料三角函数叠加问问题探究活动升旗中的数学问题必修五第一章数列1.数列1.1数列的概念1.2数列的函数特性2.等差数列2.1等差数列2.2等差数列的前n项和3.等比数列3.1等比数列3.2等比数列的前n项和4.数列在日常经济生活中的应用课题学习教育储蓄第二章解三角形1.正弦定理与余弦定理1.1正弦定理1.2余弦定理2.三角形中的几何计算3.解三角形的实际应用举例第三章不等式1.不等关系1.1不等关系1.2比较关系2.一元二次不等式2.1一元二次不等式的解法2.2一元二次不等式的应用3.基本不等式3.1基本不等式3.2基本不等式与最大（小）值4.简单线性规划4.1二元一次不等式（组）与平面区域4.2简单线性规划4.3简单线性规划的应用阅读材料人的潜能探究活动三角测量选修1-1第一章常用逻辑用语1.命题2.充分条件与必要条件3.全称量词与存在量词4.逻辑联结词“且”“或”“非”第二章圆锥曲线与方程1.椭圆2.抛物线3.双曲线阅读材料1 圆锥曲线的光学性质阅读材料2 曲线与方程第三章变化率与导数1.变化的快慢与变化率2.导数的概念及其几何意义3.计算导数4.导数的四则运算法则第四章导数应用1.函数的单调性与极值2.导数在实际问题中的应用阅读材料数学史上的丰碑——微积分选修1-2第一章统计案例1.回归分析1.1回归分析1.2相关系数1.3可线性化的回归分析阅读材料高尔顿与回归2.独立性检验2.1条件概率与独立事件阅读材料概率与法庭2.2独立性检验2.3独立性检验的基本思想2.4独立性检验的应用统计活动学习成绩与视力之间的关系第二章框图1.流程图2.结构图第三章推理与证明1.归纳与类比1.1归纳推理1.2类比推理2.数学证明3.综合法与分析法3.1综合法3.2分析法4.反证法第四章数系的扩充与复数的引入1.数系的扩充与复数的引入1.1数的概念的扩展1.2复数的有关概念2.复数的四则运算2.1复数的加法与减法2.2复数的乘法与除法阅读材料数的扩充选修2-1第一章常用逻辑用语1.命题2.充分条件与必要条件2.1充分条件2.2必要条件2.3充要条件3.全称量词与存在量词3.1全称量词与全称命题3.2存在量词与特称命题3.3全称命题与特称命题的否定4.逻辑联结词“且”“或”“非”4.1逻辑联结词“且”4.2逻辑联结词“或”4.3逻辑联结词“非”第二章空间向量与立体几何1.从平面向量到空间向量2.空间向量的运算3.向量的坐标表示和空间向量基本定理3.1空间向量的标准正交分解与坐标表示3.2空间向量基本定理3.3空间向量运算的坐标表示4.用向量讨论垂直与平行5.夹角的计算5.1直线间的夹角5.2平面间的夹角5.3直线与平面的夹角6.距离的计算课题学习空间向量在力学中的应用第三章圆锥曲线与方程1.椭圆1.1椭圆及其标准方程1.2椭圆的简单性质2.抛物线2.1抛物线及其标准方程2.2抛物线的简单性质3.双曲线3.1双曲线及其标准方程3.2双曲线的简单性质4.曲线与方程4.1曲线与方程4.2圆锥曲线的共同特征4.3直线与圆锥曲线的交点阅读材料1 圆锥曲线的光学性质阅读材料2 圆与椭圆选修2-2第一章推理与证明1.归纳与类比2.综合法与分析法3.反证法4.数学归纳法第二章变化率与导数1.变化的快慢与变化率2.导数的概念及其几何意义3.计算导数4.导数的四则运算法则5.简单复合函数的求导法则第三章导数应用1.函数的单调性与极值2.导数在实际问题中的应用第四章定积分1.定积分的概念2.微积分基本定理3.定积分的简单应用阅读材料数学史上的丰碑——微积分第五章数系的扩充与复数的引入1.数系的扩充与复数的引入2.复数的四则运算阅读材料数的扩充选修2-2 综合练习探究活动包装的设计附录1 常用函数积分公式表选修2-3第一章计数原理1.分类加法计数原理和分步乘法计数原理2.排列3.组合4.简单计数问题5.二项式定理第二章概率1.离散型随机变量及其分布列2.超几何分布3.条件概率与独立事件4.二项分布5.离散型随机变量的均值与方差6.正态分布第三章统计案例1.回归分析2.独立性检验统计活动学习成绩与视力之间的关系选修2-3 综合练习附录1 模拟“投掷一枚均匀的硬币100次”试验的程序选修3-1第一章数学发展概述1.从数学的起源、早期发展到初等数学形成2.从变量数学到现代数学第二章数与符号1.数的表示与十进制2.数的扩充3.数学符号第三章几何学发展史1.从经验几何到演绎几何2.投影画与射影几何3.解析几何第四章数学史上的丰碑——微积分1.积分思想的渊源2.圆周率3.微积分第五章无限1.初识无限2.实数集的基数第六章名题赏析1.费马大定理2.哥尼斯堡七桥问题3.高次方程4.中国剩余定理5.哥德巴赫猜想附录2 阿基米德的平衡法推导球的体积选修3-3第一章球面的基本性质1.直线、平面与球面的位置关系2.球面直线与球面距离第二章球面上的三角形1.球面三角形2.球面三角形的全等3.球面三角形的边角关系4.球面三角形的面积第三章欧拉公式与非欧几何1.球面上的欧拉公式2.简单多面体的欧拉公式3.欧氏几何与球面几何的比较附录1 立体几何中的几个概念和性质选修3-4第一章平面图形的对称性1.平面图形的对称性2.变换与平面图形的对称性阅读材料等距变换3.变换的合成4.恒等变换、可逆变换第二章平面图形的对称群1.平面图形的对称群2.有向正多边形的对称群3.正多边形的对称群第三章置换1.置换与置换群2.多面体的对称性群3.多项式的对称性阅读材料伽罗瓦理论4.群的定义选修4-1第一章直线、多边形、圆1. 全等与相似2. 圆与直线3. 圆与四边形阅读材料定长闭曲线最大面积问题第二章圆锥曲线1.截面欣赏2.直线与球、平面与球的位置关系3.柱面与平面的截面4.平面截圆锥面5.圆锥曲线的几何性质选修4-2引言第一章平面向量与二阶方阵1.平面向量及向量的运算2.向量的坐标表示及直线的向量方程3.二阶方阵与平面向量的乘法第二章几何变换与矩阵1.几种特殊的矩阵变换2.矩阵变换的性质第三章变换的合成与矩阵乘法1.变换的合成与矩阵乘法2.矩阵乘法的性质第四章逆变换与逆矩阵1.逆变换与逆矩阵2.初等变换与逆矩阵3.二阶行列式与逆矩阵4.可逆矩阵与线性方程组第五章矩阵的特征值与特征向量1.矩阵变换的特征值与特征向量2.特征向量在生态模型中的简单应用选修4-4第一章坐标系1.平面直角坐标系2.极坐标系3.极坐标系和球坐标系阅读材料笛卡尔与坐标系第二章参数方程1.参数方程的概念2.直线和圆锥曲线的参数方程3.参数方程化成普通方程4.平摆线和渐开线阅读材料1 其他摆线阅读材料2 摆线的应用研究选修4-5第一章不等关系与基本不等式1.不等式的性质2.含有绝对值的不等式3.平均值不等式4.不等式的证明5.不等式的应用第二章几个重要的不等式1.柯西不等式2.排序不等式3.数学归纳法与贝努利不等式选修4-6第一章带余除法与数的进位制1. 整除与带余除法1.1整除1.2带余除法2. 二进制课题学习三进制阅读材料进位制第二章可约性1.素数与合数1.1素数的判别1.2素数的个数2.最大公因数与辗转相除法3.算术基本定理及其应用3.1算术基本定理3.2最小公倍数与算术基本定理的应用阅读材料费马数与梅森数4.不定方程第三章同余1.同余及其应用1.1同余1.2同余的性质1.3整除的判断与弃九法2.欧拉定理2.1剩余类2.2欧拉定理?费马小定理阅读材料公开密钥——RSA 体制3.同余方程（组）3.1同余方程（组）3.2孙子定理选修4-7第一章正交试验设计1.试验设计2.拉丁方与试验设计2.1实例分析2.2拉丁方2.3拉丁方设计3.多因素试验设计3.1多因素试验3.2常见试验设计方案3.3实例分析——微波炉加工爆米花4.试验的均衡搭配与正交表4.1试验设计的基本原则——均衡搭配4.2正交表及其基本特征4.3正交表5.正交试验设计5.1利用正交表确定试验方案5.2实例分析阅读材料交互作用第二章优选法1.单因素优选法1.1单因素优选问题及其处理方法1.2误差估计2.分数法2.1两次试验分数法的试验设计2.2三次试验分数法的试验设计2.3 n次试验分数法的试验设计2.4分数法的应用3.0.618法3.1 0.618法3.2 0.618法的应用阅读材料几种有用的选纵横对折法课题学习选题、试验并完成试验报告阅读材料华罗庚与优选法附录2 n次分数法的证明。