9年级4.3—二次函数背景下的特殊图形问题

初三二次函数的图像与性质二次函数是初中数学中的一个重要概念。

在数学学习的过程中，我们常常会接触到二次函数，并且需要了解它的图像特点以及性质。

本文将详细介绍初三二次函数的图像和性质，并且给出相关的例题和解析。

一、二次函数的定义及一般式二次函数是指函数$y=ax^2+bx+c$，其中$a,b,c$为常数且$a\neq 0$。

它的图像是抛物线，并且开口的方向由$a$的正负决定。

当$a>0$时，抛物线开口向上；而当$a<0$时，抛物线开口向下。

二次函数的一般式为$y=ax^2+bx+c$，其中$a,b,c$为常数。

其中，$a$代表抛物线的开口方向与开口的大小，$b$影响抛物线的位置，$c$影响抛物线和$y$轴的交点。

【例题1】某二次函数的方程是$y=2x^2-3x+1$，求该二次函数的图像和性质。

解：根据给定的二次函数方程，我们可以得到$a=2$，$b=-3$，$c=1$。

由于$a>0$，所以抛物线开口向上。

考虑二次函数的图像特点，我们可以使用一些方法来绘制它的图像。

首先，我们可以找出抛物线的对称轴，对称轴的方程为$x=-\frac{b}{2a}$。

代入$a=2$，$b=-3$，我们得到$x=-\frac{-3}{2\times2}=\frac{3}{4}$。

因此，对称轴的方程为$x=\frac{3}{4}$。

接下来，我们需要计算抛物线的顶点坐标。

顶点坐标可以通过将对称轴的$x$坐标代入原函数方程计算得到。

将$x=\frac{3}{4}$代入$y=2x^2-3x+1$，我们得到$y=2(\frac{3}{4})^2-3(\frac{3}{4})+1=\frac{9}{8}-\frac{9}{4}+1=\frac{1}{8}$。

因此，顶点坐标为$(\frac{3}{4}, \frac{1}{8})$。

不难看出，根据顶点的坐标和对称轴的方程，我们可以绘制出该二次函数的图像。

它是一个开口向上的抛物线，对称轴为$x=\frac{3}{4}$，顶点坐标为$(\frac{3}{4}, \frac{1}{8})$。

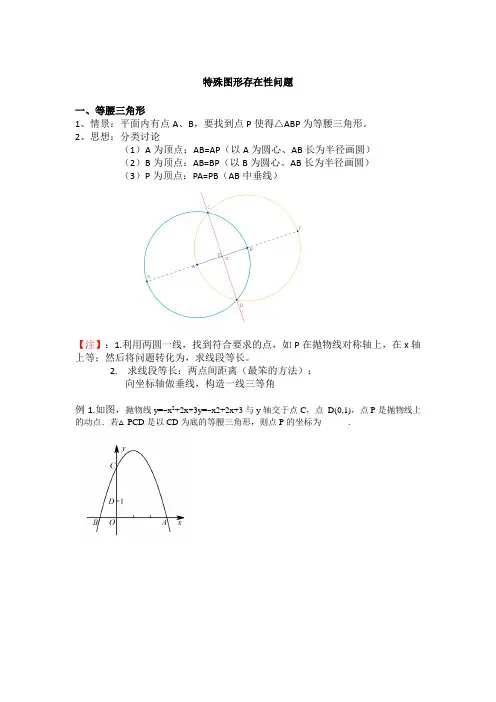
特殊图形存在性问题一、等腰三角形1、情景：平面内有点A、B，要找到点P使得△ABP为等腰三角形。

2、思想：分类讨论（1）A为顶点：AB=AP（以A为圆心、AB长为半径画圆）（2）B为顶点：AB=BP（以B为圆心、AB长为半径画圆）（3）P为顶点：PA=PB（AB中垂线）【注】：1.利用两圆一线，找到符合要求的点，如P在抛物线对称轴上，在x轴上等；然后将问题转化为，求线段等长。

2.求线段等长：两点间距离（最笨的方法）；向坐标轴做垂线，构造一线三等角例1.如图，抛物线y=−x2+2x+3y=−x2+2x+3与y轴交于点C，点D(0,1)，点P是抛物线上的动点．若△PCD是以CD为底的等腰三角形，则点P的坐标为______．练习1.如图，在平面直角坐标系中，二次函数y=x2+bx+c的图象与x轴交于A,B 两点，A点在原点的左侧，B点的坐标为(3,0)，与y轴交于C(0,−3)点，点P是直线BC下方的抛物线上一动点．(1)求这个二次函数的表达式；(2)在直线BC找一点Q，使得△QOC为等腰三角形，写出Q点坐标．练习2、已知抛物线y=ax2+bx+c经过A（﹣1，0）、B（3，0）、C（0，3）三点，直线l 是抛物线的对称轴．（1）求抛物线的函数关系式；（2）设点P是直线l上的一个动点，当△PAC的周长最小时，求点P的坐标；（3）在直线l上是否存在点M，使△MAC为等腰三角形？若存在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由．练习3.如图，抛物线y=ax2+bx﹣3（a≠0）的顶点为E，该抛物线与x轴交于A、B两点，与y轴交于点C，且BO=OC=3AO，直线y=﹣x+1与y轴交于点D．（1）求抛物线的解析式；（2）证明：△DBO∽△EBC；（3）在抛物线的对称轴上是否存在点P，使△PBC是等腰三角形？若存在，请直接写出符合条件的P点坐标，若不存在，请说明理由．练习4.如图，在平面直角坐标系中，已知抛物线y=ax2+bx+c(a≠0)与x轴交A(−1,0),B(−3,0)两点，与y轴交于点C(0,−3)，其顶点为D．(1)求该抛物线的解析式，并用配方法把解析式化为y=a(x−h)2+k的形式；(2)动点M从点D出发，沿抛物线对称轴方向向上以每秒1个单位的速度运动，运动时间为t，连接OM,BM，当t为何值时，△OMB为等腰三角形？练习5.如图，在平面直角坐标系中，点A的坐标为（m，m），点B的坐标为（n，﹣n），抛物线经过A、O、B三点，连接OA、OB、AB，线段AB交y轴于点C．已知实数m、n （m＜n）分别是方程x2﹣2x﹣3=0的两根．（1）求抛物线的解析式；（2）若点P为线段OB上的一个动点（不与点O、B重合），直线PC与抛物线交于D、E 两点（点D在y轴右侧），连接OD、BD．①当△OPC为等腰三角形时，求点P的坐标；②求△BOD 面积的最大值，并写出此时点D的坐标．25．（10分）如图，在平面直角坐标系中，抛物线y＝x2+bx+c经过原点O，与x轴交于点A（5，0），第一象限的点C（m，4）在抛物线上，y轴上有一点B（0，10）．（Ⅰ）求抛物线的解析式及它的对称轴；（Ⅱ）点P（0，n）在线段OB上，点Q在线段BC上，若OP＝2BQ，且P A＝QA．求n 的值；（Ⅲ）在抛物线的对称轴上，是否存在点M，使以A，B，M为顶点的三角形是等腰三角形？若存在，求出点M的坐标；若不存在，请说明理由．19-红桥一模25．（10分）如图，抛物线y＝x2+bx+c与y轴交于点C（0，﹣4），与x轴交于点A，B，且B点的坐标为（2，0）．（1）求该抛物线的解析式．（2）若点P是AB上的一动点，过点P作PE∥AC，交BC于E，连接CP，求△PCE面积的最大值．（3）若点D为OA的中点，点M是线段AC上一点，且△OMD为等腰三角形，求M点的坐标．(17河北一模)25(10分）如图，己知抛物线y=x2+bx+c图象经过点A（﹣1，0），B（0，﹣3），抛物线与x轴的另一个交点为C．（1）求这个抛物线的解析式：（2）若抛物线的对称轴上有一动点D，且△BCD为等腰三角形（CB≠CD），试求点D的坐标；二、直角三角形1.情景：平面内有点A、B，要找到点P使得△ABP为直角三角形2.思想：分类讨论（1）A为顶点：∠A（过A做垂线）（2）B为顶点：∠B（过B做垂线）（3）P为顶点：∠C（AB为直径的圆）【注】1.等腰直角三角形，只需在两直线上上下找与AB等长以及过O做AB垂线与圆交点即可例1.如图，在平面直角坐标系中，二次函数y=ax2+bx+c的图象经过矩形OABC的顶点A，B与x 轴交于点E，F且B，E两点的坐标分别为B(2，32)E(−1，0)(1)求二次函数的解析式；(2)在抛物线上是否存在点Q，使△QBF为直角三角形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．练习1.如图，抛物线y=x2+bx+3顶点为P，且分别与x轴、y轴交于A、B两点，点A在点P的右侧，tan∠ABO=13(1)求抛物线的对称轴和PP的坐标．(2)在抛物线的对称轴上是否存在这样的点D，使△ABD为直角三角形？如果存在，求点D 的坐标；如果不存在，请说明理由．例2.如图，抛物线y=−x2+bx+c与x轴相交于AB两点，与y 轴相交与点C，且点B与点CC 的坐标分别为(3,0)，C(0,3)，点M是抛物线的顶点．(1)求二次函数的关系式(2)在MB上是否存在点P，过点P作PD⊥x轴于点D,OD=m,使△PCD为直角三角形？如果存在，请直接写出点P的坐标；如果不存在，请说明理由练习2.如图，在平面直角坐标系中，直线y=−13x+2交x轴点P，交y轴于点A．抛物线y=x2+bx+c的图象过点E(−1,0)，并与直线相交于A、B两点．(1)求抛物线的解析式（关系式）；(2)过点A作AC⊥AB交x轴于点C，求点C的坐标；(3)除点C外，在坐标轴上是否存在点M，使得△MAB是直角三角形？若存在，请求出点M 的坐标；若不存在，请说明理由．练习3.如图，抛物线y=x2+bx+c与直线y=x﹣3交于A、B两点，其中点A在y轴上，点B坐标为（﹣4，﹣5），点P为y轴左侧的抛物线上一动点，过点P作PC⊥x轴于点C，交AB于点D．（1）求抛物线的解析式；（2）以O，A，P，D为顶点的平行四边形是否存在？如存在，求点P的坐标；若不存在，说明理由．（3）当点P运动到直线AB下方某一处时，过点P作PM⊥AB，垂足为M，连接PA使△PAM为等腰直角三角形，请直接写出此时点P的坐标．（18东丽-一模）25.如图，在平面直角坐标系中，点A、B的坐标分别为（1，1）、（1，2），过点A、B分别作y轴的垂线，垂足为D、C，得到正方形ABCD，抛物线y=x2+bx+c经过A、C两点，点P为第一象限内抛物线上一点（不与点A重合），过点P分别作x轴y轴的垂线，垂足为E、F，设点P的横坐标为m，矩形PFOE与正方形ABCD重叠部分图形的周长为l．（1）直接写出抛物线所对应的函数表达式．（2）当矩形PFOE的面积被抛物线的对称轴平分时，求m的值．（3）当m＜2时，求L与m之间的函数关系式．（4）设线段BD与矩形PFOE的边交于点Q，当△FDQ为等腰直角三角形时，直接写出m的取值范围．三、平行四边形存在性问题类型一：1.情景：一直平面内三点A、B、C，求一点P使四边形ABCP为平行四边形2.思想：分类讨论（1）以AC为对角线：ABCP1（2）以AB为对角线：ACBP3（3）以BC为对角线：ACP2B【注】找到P点后，用平行四边形的判定定理，求等长线段，或利用等角度、平行线求坐标即可。

二次函数的图象与性质大题（五大题型）通用的解题思路：题型一．二次函数的性质二次函数y＝ax2+bx+c（a≠0）的顶点坐标是（﹣，），对称轴直线x＝﹣，二次函数y＝ax2+bx+c （a≠0）的图象具有如下性质：①当a＞0时，抛物线y＝ax2+bx+c（a≠0）的开口向上，x＜﹣时，y随x的增大而减小；x＞﹣时，y随x的增大而增大；x＝﹣时，y取得最小值，即顶点是抛物线的最低点．②当a＜0时，抛物线y＝ax2+bx+c（a≠0）的开口向下，x＜﹣时，y随x的增大而增大；x＞﹣时，y随x的增大而减小；x＝﹣时，y取得最大值，即顶点是抛物线的最高点．③抛物线y＝ax2+bx+c（a≠0）的图象可由抛物线y＝ax2的图象向右或向左平移|﹣|个单位，再向上或向下平移||个单位得到的．题型二．二次函数图象与系数的关系二次函数y＝ax2+bx+c（a≠0）①二次项系数a决定抛物线的开口方向和大小．当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；|a|还可以决定开口大小，|a|越大开口就越小．②一次项系数b和二次项系数a共同决定对称轴的位置．当a与b同号时（即ab＞0），对称轴在y轴左侧；当a与b异号时（即ab＜0），对称轴在y轴右侧．（简称：左同右异）③．常数项c决定抛物线与y轴交点．抛物线与y轴交于（0，c）．④抛物线与x轴交点个数．△＝b2﹣4ac＞0时，抛物线与x轴有2个交点；△＝b2﹣4ac＝0时，抛物线与x轴有1个交点；△＝b2﹣4ac ＜0时，抛物线与x轴没有交点．题型三．待定系数法求二次函数解析式（1）二次函数的解析式有三种常见形式：①一般式：y＝ax2+bx+c（a，b，c是常数，a≠0）；②顶点式：y＝a（x﹣h）2+k（a，h，k是常数，a≠0），其中（h，k）为顶点坐标；③交点式：y＝a（x﹣x1）（x﹣x2）（a，b，c是常数，a≠0）；（2）用待定系数法求二次函数的解析式．在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解．一般地，当已知抛物线上三点时，常选择一般式，用待定系数法列三元一次方程组来求解；当已知抛物线的顶点或对称轴时，常设其解析式为顶点式来求解；当已知抛物线与x轴有两个交点时，可选择设其解析式为交点式来求解．题型四．抛物线与x轴的交点求二次函数y＝ax2+bx+c（a，b，c是常数，a≠0）与x轴的交点坐标，令y＝0，即ax2+bx+c＝0，解关于x 的一元二次方程即可求得交点横坐标．（1）二次函数y＝ax2+bx+c（a，b，c是常数，a≠0）的交点与一元二次方程ax2+bx+c＝0根之间的关系．△＝b2﹣4ac决定抛物线与x轴的交点个数．△＝b2﹣4ac＞0时，抛物线与x轴有2个交点；△＝b2﹣4ac＝0时，抛物线与x轴有1个交点；△＝b2﹣4ac＜0时，抛物线与x轴没有交点．（2）二次函数的交点式：y＝a（x1）（x﹣x2）（a，b，c是常数，a≠0），可直接得到抛物线与x轴的交点坐标（x1，0），（x2，0）．题型五．二次函数综合题（1）二次函数图象与其他函数图象相结合问题解决此类问题时，先根据给定的函数或函数图象判断出系数的符号，然后判断新的函数关系式中系数的符号，再根据系数与图象的位置关系判断出图象特征，则符合所有特征的图象即为正确选项．（2）二次函数与方程、几何知识的综合应用将函数知识与方程、几何知识有机地结合在一起．这类试题一般难度较大．解这类问题关键是善于将函数问题转化为方程问题，善于利用几何图形的有关性质、定理和二次函数的知识，并注意挖掘题目中的一些隐含条件．（3）二次函数在实际生活中的应用题从实际问题中分析变量之间的关系，建立二次函数模型．关键在于观察、分析、创建，建立直角坐标系下的二次函数图象，然后数形结合解决问题，需要我们注意的是自变量及函数的取值范围要使实际问题有意义．题型一．二次函数的性质（共3小题）1．（2024•石景山区校级模拟）在平面直角坐标系xOy 中，1(A x ，1)y ，2(B x ，2)y 是抛物线2(0)y x bx b =−+≠上任意两点，设抛物线的对称轴为直线x h =． （1）若抛物线经过点(2,0)，求h 的值；（2）若对于11x h =−，22x h =，都有12y y >，求h 的取值范围；（3）若对于121h x h −+……，221x −−……，存在12y y <，直接写出h 的取值范围． 【分析】（1）根据对称轴2bx a=−进行计算，得2b h =，再把(2,0)代入2(0)y x bx b =−+≠，即可作答．（2）因为1(A x ，1)y ，2(B x ，2)y 是抛物线2(0)y x bx b =−+≠上的点，所以把11x h =−，22x h =分别代入，得出对应的1y ，2y ，再根据12y y >联立式子化简，计算即可作答；（3）根据121h x h −+……，221x −−……，存在12y y <，得出当221h −<−<−或者211h −<+<−，即可作答． 【解答】解：（1）抛物线的对称轴为直线x h =， 22b bh ∴=−=−， 即2b h =，∴抛物线22y x hx =−+，把(2,0)代入22y x hx =−+， 得0422h =−+⨯， 解得1h =；（2）由（1）知抛物线22y x hx =−+，1(A x ，1)y ，2(B x ，2)y 是抛物线22y x hx =−+上任意两点，221(1)2(1)1y h h h h ∴=−−+−=−，22(2)220y h h h =−+⨯=，对于11x h =−，22x h =，都有12y y >， 210h ∴−>，解得1h >或1h <−；（3）1(A x ，1)y ，2(B x ，2)y 是抛物线22y x hx =−+上任意两点，对于121h x h −+……，221x −−……，存在12y y <，且1(2,)h y −关于直线x h =的对称点为1(2,)h y +，1(1,)h y +关于直线x h =的对称点为1(1,)h y −，∴当221h −<−<−时，存在12y y <，解得01h <<，当221h −<+<−时，存在12y y <， 解得43h −<<−，当211h −<+<−时，存在12y y <， 解得32h −<<−，当211h −<−<−时，存在12y y <， 解得10h −<<，综上，满足h 的取值范围为41h −<<且0h ≠．【点评】本题考查了二次函数的图象性质、增减性，熟练掌握二次函数的图象和性质是解决本题的关键． 2．（2024•鹿城区校级一模）已知二次函数223y x tx =−++． （1）若它的图象经过点(1,3)，求该函数的对称轴． （2）若04x ……时，y 的最小值为1，求出t 的值．（3）如果(2,)A m n −，(,)C m n 两点都在这个二次函数的图象上，直线2y mx a =+与该二次函数交于1(M x ，1)y ，2(N x ，2)y 两点，则12x x +是否为定值？若是，请求出该定值；若不是，请说明理由．【分析】（1）把(1,3)代入解析式求出12t =，再根据对称轴公式求出对称轴； （2）根据抛物线开口向下，以及0x =时3y =，由函数的性质可知，当4x =时，y 的最小值为1，然后求t 即可；（3）(2,)A m n −，(,)C m n 两点都在这个二次函数的图象上，有对称轴公式得出1m t −=，再令2232x tx mx a −++=+，并转化为一般式，然后由根与系数的关系求出122x x +=−．【解答】解：（1）将(1,3)代入二次函数223y x tx =−++，得3123t =−++， 解得12t =， ∴对称轴直线为21122t x t =−==−⨯； （2）当0x =时，3y =，抛物线开口向下，对称轴为直线x t =， ∴当x t =时，y 有最大值，04x ……时，y 的最小值为1，∴当4x =时，16831y t =−++=，解得74t =； （3）12x x +是定值，理由：(2,)A m n −，(,)C m n 两点都在这个二次函数的图象上， 212m mx t m −+∴===−， 1m t ∴−=，令2232x tx mx a −++=+， 整理得：22()30x m t x a +−+−=，直线2y mx a =+与该二次函数交于1(M x ，1)y ，2(N x ，2)y 两点， 1x ∴，2x 是方程22()30x m t x a +−+−=的两个根，122()2()21m t x x m t −∴+=−=−−=−是定值． 【点评】本题考查了二次函数的性质，二次函数图象上点的坐标特征等知识，关键是掌握二次函数的性质． 3．（2024•拱墅区一模）在平面直角坐标系中，抛物线2(2)2y ax a x =−++经过点(2,)A t −，(,)B m p ． （1）若0t =，①求此抛物线的对称轴；②当p t <时，直接写出m 的取值范围；（2）若0t <，点(,)C n q 在该抛物线上，m n <且5513m n +<−，请比较p ，q 的大小，并说明理由． 【分析】（1）①当0t =时，点A 的坐标为(2,0)−，将其代入函数解析式中解得1a =−，则函数解析式为抛物线的解析式为22y x x =−−+，再根据求对称轴的公式2bx a=−即可求解； ②令0y =，求出抛物线与x 轴交于(2,0)−和(1,0)，由题意可得0p <，则点B 在x 轴的下方，以此即可解答； （2）将点A 坐标代入函数解析式，通过0t <可得a 的取值范围，从而可得抛物线开口方向及对称轴，根据点B ，C 到对称轴的距离大小关系求解．【解答】解：（1）①当0t =时，点A 的坐标为(2,0)−，抛物线2(2)2y ax a x =−++经过点(2,0)A −， 42(2)20a a ∴+++=，1a ∴=−，∴抛物线的解析式为22y x x =−−+， ∴抛物线的对称轴为直线112(1)2x −=−=−⨯−；②令0y =，则220x x −−+=， 解得：11x =，22x =−，∴抛物线与x 轴交于(2,0)−和(1,0)，点(2,0)A −，(,)B m p ，且0p <， ∴点(,)B m p 在x 轴的下方，2m ∴<−或1m >．（2）p q <，理由如下：将(2,)t −代入2(2)2y ax a x =−++得42(2)266t a a a =+++=+，0t <， 660a ∴+<， 1a ∴<−，∴抛物线开口向下，抛物线对称轴为直线(2)1122a x a a −+=−=+， 1a <−，110a∴−<<， 1111222a ∴−<+<， m n <且5513m n +<−，∴1312102m n +<−<−， ∴点(,)B m p 到对称轴的距离大于点(,)C n q 到对称轴的距离，p q ∴<．【点评】本题考查二次函数的综合应用，解题关键是掌握二次函数的性质，掌握二次函数与方程及不等式的关系．题型二．二次函数图象与系数的关系（共8小题）4．（2023•南京）已知二次函数223(y ax ax a =−+为常数，0)a ≠． （1）若0a <，求证：该函数的图象与x 轴有两个公共点． （2）若1a =−，求证：当10x −<<时，0y >．（3）若该函数的图象与x 轴有两个公共点1(x ，0)，2(x ，0)，且1214x x −<<<，则a 的取值范围是 ．【分析】（1）证明240b ac −>即可解决问题． （2）将1a =−代入函数解析式，进行证明即可． （3）对0a >和0a <进行分类讨论即可．【解答】证明：（1）因为22(2)43412a a a a −−⨯⨯=−， 又因为0a <，所以40a <，30a −<， 所以24124(3)0a a a a −=−>，所以该函数的图象与x 轴有两个公共点． （2）将1a =−代入函数解析式得，2223(1)4y x x x =−++=−−+，所以抛物线的对称轴为直线1x =，开口向下． 则当10x −<<时，y 随x 的增大而增大， 又因为当1x =−时，0y =， 所以0y >．（3）因为抛物线的对称轴为直线212ax a−=−=，且过定点(0,3)， 又因为该函数的图象与x 轴有两个公共点1(x ，0)，2(x ，0)，且1214x x −<<<， 所以当0a >时，230a a −+<， 解得3a >， 故3a >．当0a <时，230a a ++<，解得1a <−， 故1a <−．综上所述，3a >或1a <−． 故答案为：3a >或1a <−．【点评】本题考查二次函数的图象和性质，熟知二次函数的图象和性质是解题的关键．5．（2024•南京模拟）在平面直角坐标系xOy 中，点1(1,)y ，2(3,)y 在抛物线222y x mx m =−+上． （1）求抛物线的顶点(,0)m ； （2）若12y y <，求m 的取值范围；（3）若点0(x ，0)y 在抛物线上，若存在010x −<<，使102y y y <<成立，求m 的取值范围． 【分析】（1）利用配方法将已知抛物线解析式转化为顶点式，可直接得到答案； （2）由12y y <，得到221296m m m m −+<−+，解不等式即可； （3）由题意可知012032m m +⎧<⎪⎪⎨+⎪>⎪⎩或112132m m −+⎧<⎪⎪⎨−+⎪>⎪⎩，解不等式组即可．【解答】解：（1）抛物线222()y x mx m x m =−+=−． ∴抛物线的顶点坐标为(,0)m ．故答案为：(,0)m ；（2）点1(1,)y ，2(3,)y 在抛物线222y x mx m =−+上，且12y y <， 221296m m m m ∴−+<−+，2m ∴<；（3）点0(x ，0)y 在抛物线上，存在010x −<<，使102y y y <<成立， ∴012032m m +⎧<⎪⎪⎨+⎪>⎪⎩或112132m m −+⎧<⎪⎪⎨−+⎪>⎪⎩，解得302m <<． 【点评】本题考查了二次函数与系数的关系，二次函数图象上点的坐标特征，熟知二次函数的性质是解题的关键．6．（2024•北京一模）在平面直角坐标系中，已知抛物线23y ax bx =++经过点(2,3)a −． （1）求该抛物线的对称轴（用含有a 的代数式表示）；（2）点(2,)M t m −，(2,)N t n +，(,)P t p −为该抛物线上的三个点，若存在实数t ，使得m n p >>，求a 的取值范围．【分析】（1）将点(2,3)a −代入抛物线23y ax bx =++中，然后根据二次函数的对称轴公式代入数值，即可得出答案；（2）分类讨论当0a >和0a <，利用数形结合以及二次函数的性质就可以得出a 的取值范围． 【解答】解（1）抛物线23y ax bx =++经过点(2,3)a −， ∴把(2,3)a −代入23y ax bx =++得2(2)233a a ab ⨯−−+=，22b a ∴=，2223y ax a x ∴=++，∴抛物线的对称轴222a x a a=−=−，答：抛物线的对称轴为：x a =−；（2）①当0a >时，抛物线开口方向向上，对称轴0x a =−<，在x 轴的负半轴上，所以越靠近对称轴函数值越小， ∴当0t <时，(2,)M t m −，(2,)N t n +，(,)P t p −在抛物线上，22t t ∴−<+，∴此时p m n >>与题干m n p >>相矛盾，故舍去， ∴当0t >时，(2,)M t m −，(2,)N t n +，(,)P t p −在抛物线上，22t t ∴−<+，∴此时m n <与题干m n p >>相矛盾，故舍去；②当0a <时，抛物线开口方向向下，对称轴0x a =−>，在x 轴的正半轴上，所以越靠近对称轴函数值越大， ∴当0t >时，点M 、N 分别在对称轴同侧时，(2,)M t m −，(2,)N t n +，(,)P t p −在抛物线上，22t t ∴−<+， .m n p >>，∴此时02a t <−<−，即20t a −<<，2t ∴>，∴当0t >时，点M 、N 分别在对称轴两侧时，(2,)M t m −，(2,)N t n +，(,)P t p −在抛物线上，22t t t ∴−<<+，p m n ∴>>与题干m n p >>相矛盾，故舍去，∴当0t <时，且点M 、N 分别在对称轴两侧时，(2,)M t m −，(2,)N t n +，(,)P t p −在抛物线上，22t t t ∴−<<+，n m ∴>与题干m n p >>相矛盾，故舍去，当0t <时，且点M 、N 分别在对称轴同侧时， (2,)M t m −，(2,)N t n +，(,)P t p −在抛物线上，22t t t ∴−<<+，n m ∴>与题干m n p >>相矛盾，故舍去，答：a 的取值范围为20(2)t a t −<<>．7．（2024•张家口一模）某课外小组利用几何画板来研究二次函数的图象，给出二次函数解析式2y x bx c =++，通过输入不同的b ，c 的值，在几何画板的展示区内得到对应的图象．（1）若输入2b =，3c =−，得到如图①所示的图象，求顶点C 的坐标及抛物线与x 轴的交点A ，B 的坐标； （2）已知点(1,10)P −，(4,0)Q ．①若输入b ，c 的值后，得到如图②的图象恰好经过P ，Q 两点，求出b ，c 的值；②淇淇输入b ，嘉嘉输入1c =−，若得到二次函数的图象与线段PQ 有公共点，求淇淇输入b 的取值范围．【分析】（1）将2b =，3c =−，代入函数解析式，进行求解即可； （2）①待定系数法进行求解即可；②将1c =−代入解析式，得到抛物线必过点(0,1)−，求出1x =−和4x =的函数值，根据抛物线与线段PQ 有公共点，列出不等式进行求解即可． 【解答】解：（1）2y x bx c =++，解：当2b =，3c =−时，2223(1)4y x x x =+−=+−， ∴顶点C 的坐标为：(1,4)−−；当0y =时，2230x x +−=，即(3)(1)0x x +−=， 解得：13x =−，21x =， (3,0)A ∴−，(1,0)B ；（2）①抛物线恰好经过P ，Q则：1101640b c b c −+=⎧⎨++=⎩，解得：54b c =−⎧⎨=⎩；②当1c =−时，21y x bx =+−， 当0x =时，1y =−， ∴抛物线过(0,1)−，当1x =−时，11y b b =−−=−，当点(1,)b −−在点P 上方，或与点P 重合时，抛物线与线段PQ 有公共点，即：10b −…， 解得：10b −…；当4x =时，1641415y b b =+−=+，当点(4,154)b +在点Q 上方，或与点Q 重合时，抛物线与线段PQ 有公共点，即：1540b +…，154b ≥−； 综上：10b −…或154b ≥−． 【点评】本题考查二次函数的综合应用．正确的求出函数解析式，熟练掌握二次函数的图象和性质是解题的关键．8．（2024•浙江模拟）设二次函数24(y ax ax c a =−+，c 均为常数，0)a ≠，已知函数值y 和自变量x 的部分对应取值如下表所示：（1）判断m ，n 的大小关系，并说明理由； （2）若328m n −=，求p 的值；（3）若在m ，n ，p 这三个数中，只有一个数是负数，求a 的取值范围．【分析】（1）根据所给函数解析式，可得出抛物线的对称轴为直线2x =，据此可解决问题． （2）根据（1）中发现的关系，可求出m 的值，据此即可解决问题． （3）根据m 和n 相等，所以三个数中的负数只能为p ，据此可解决问题． 【解答】解：（1）m n =．因为二次函数的解析式为24y ax c =+， 所以抛物线的对称轴为直线422ax a−=−=， 又因为1522−+=， 所以点(1,)m −与(5,)n 关于抛物线的对称轴对称， 故m n =．（2）因为m n =，328m n −=， 所以8m =．将(0,3)和(1,8)−代入函数解析式得：348c a a c =⎧⎨++=⎩，解得13a c =⎧⎨=⎩所以二次函数的解析式为243y x x =−+．将2x =代入函数解析式得，224231p =−⨯+=−．（3）由（1）知，m n =， 所以m ，n ，p 中只能p 为负数． 将(0,3)代入函数解析式得，3c =， 所以二次函数解析式为243y ax ax =−+． 将1x =−代入函数解析式得，53m a =+． 将2x =代入函数解析式得，43p a =−+．则430530a a −+<⎧⎨+≥⎩，解得34a >，所以a 的取值范围是34a >． 【点评】本题考查二次函数图象与系数的关系及二次函数图象上点的坐标特征，熟知二次函数的图象和性质是解题的关键．9．（2024•北京模拟）在平面直角坐标系xOy 中，抛物线2(26)1y x m x =+−+经过点1(,)m y −，2(,)m y ，3(2,)m y +．（1）若13y y =，求抛物线的对称轴； （2）若231y y y <<，求m 的取值范围． 【分析】（1）利用对称轴意义即可求解；（2m 的不等式组，解不等式组即可．【解答】解：（1）抛物线2(26)1y x m x =+−+经过点1(,)m y −，2(,)m y ，3(2,)m y +，13y y =， ∴该抛物线的对称轴为：直线22m m x −++=，即直线1x =； （2）当0m >时，可知点1(,)m y −，2(,)m y ，3(2,)m y +从左至右分布， 231y y y <<，∴232232m m m m m m ++⎧−<⎪⎪⎨−++⎪−>⎪⎩，解得12m <<； 当0m <时，3m m m ∴<−<−+，21y y ∴>，不合题意，综上，m 的取值范围是12m <<．【点评】本题考查了二次函数图象上点的坐标特征，二次函数的性质，熟练掌握二次函数的性质是解题的关键．10．（2024•浙江模拟）在平面直角坐标系xOy 中，抛物线2(y ax bx c a =++，b ，c 为常数，且0)a ≠经过(2,4)A −−和(3,1)B 两点．（1）求b 和c 的值（用含a 的代数式表示）；（2）若该抛物线开口向下，且经过(23,)C m n −，(72,)D m n −两点，当33k x k −<<+时，y 随x 的增大而减小，求k 的取值范围；（3）已知点(6,5)M −，(2,5)N ，若该抛物线与线段MN 恰有一个公共点时，结合函数图象，求a 的取值范围．【分析】（1）把(2,4)A −−和(3,1)B 代入2y ax bx c =++，即可求解；（2）先求出对称轴为：直线2x =，结合开口方向和增减性列出不等式即可求解； （3）分0a >时，0a <时，结合图象即可求解．【解答】解：（1）把(2,4)A −−和(3,1)B 代入2y ax bx c =++，得：424931a b c a b c −+=−⎧⎨++=⎩，解得：162b a c a =−⎧⎨=−−⎩；（2）抛物线经过(23,)C m n −，2,)m n −两点， ∴抛物线的对称轴为：直线237222m mx −+−==，抛物线开口向下，当33k x k −<<+时，y 随x 的增大而减小，32k ∴−…，即5k …； （3）①当0a >时，6x =−，5y …，即2(6)(1)(6)625a a a ⨯−+−⨯−−−…， 解得：1336a …，抛物线不经过点N ，如图①，抛物线与线段MN 只有一个交点，结合图象可知：1336a …；②当0a <时，若抛物线的顶点在线段MN 上时，则2244(62)(1)544ac b a a a a a−−−−−==，解得：11a =−，2125a =−， 当11a =−时，111112222(1)a −=−=⨯−， 此时，定点横坐标满足116222a−−……，符合题意； 当11a =−时，如图②，抛物线与线段MN 只有一个交点，如图③，当2125a =−时，11111312222()25a −=−=⨯−，此时顶点横坐标不满足116222a−−……，不符合题意，舍去； 若抛物线与线段MN 有两个交点，且其中一个交点恰好为点N 时，把(2,5)N 代入2(1)62y ax a x a =+−−−，得：252(1)262a a a =⨯+−⨯−−， 解得：54a =−，当54a =−时，如图④，抛物线和线段MN 有两个交点，且其中一个交点恰好为点N ，结合图象可知：54a <−时，抛物线与线段MN 有一个交点，综上所述：a 的取值范围为：1336a …或1a =−或54a <−．【点评】本题考查二次函数的性质和图象，根据题意画出图象，分类讨论是解题的关键．11．（2024•海淀区校级模拟）在平面直角坐标系xOy 中，点(0,3)，1(6,)y 在抛物线2(0)y ax bx c a =++≠上． （1）当13y =时，求抛物线的对称轴；（2）若抛物线2(0)y ax bx c a =++≠经过点(1,1)−−，当自变量x 的值满足12x −……时，y 随x 的增大而增大，求a 的取值范围；（3）当0a >时，点2(4,)m y −，2(,)m y 在抛物线2y ax bx c =++上．若21y y c <<，请直接写出m 的取值范围．【分析】（1）当13y =时，(0,3)，(6,3)为抛物线上的对称点，根据对称性求出对称轴；（2）把(0,3)，(1,1)−−代入抛物线解析式得出a ，b 的关系，然后求出对称轴，再分0a >和0a <，由函数的增减性求出a 的取值范围；（3）先画出函数图象，再根据21y y c <<确定m 的取值范围． 【解答】解：（1）当13y =时，(0,3)，(6,3)为抛物线上的对称点， 0632x +∴==， ∴抛物线的对称轴为直线3x =；（2）2(0)y ax bx c a =++≠过(0,3)，(1,1)−−，3c ∴=，31a b −+=−， 4b a =+，∴对称轴为直线422b a x a a+=−=−，①当0a >时，12x −……时，y 随x 的增大而增大，∴412a a+−−…， 解得4a …，04a ∴<…；②当0a <时，12x −……时，y 随x 的增大而增大，∴422a a+−…， 解得45a −…， ∴405a −<…，综上：a 的取值范围是405a −<… 或04a <…；（3）点(0,3)在抛物线2y ax bx c =++上，3c ∴=，点2(4,)m y −，2(,)m y 在抛物线2y ax bx c =++上， ∴对称轴为直线422m mx m −+==−， ①如图所示：21y y c <<，6m ∴<且06232m +−>=， 56m ∴<<；②如图所示：21y y c <<，46m ∴−>， 10m ∴>，综上所述，m 的取值范围为56m <<或10m >．【点评】本题考查二次函数图象与系数的关系以及二次函数图象上点的坐标特征，关键是利用数形结合和分类讨论的思想进行解答．题型三．待定系数法求二次函数解析式（共3小题）12．（2024•保山一模）如图，抛物线2y ax bx c =++过(2,0)A −，(3,0)B ，(0,6)C 三点；点P 是第一象限内抛物线上的动点，点P 的横坐标是m ，且132m <<． （1）试求抛物线的表达式；（2）过点P 作PN x ⊥轴并交BC 于点N ，作PM y ⊥轴并交抛物线的对称轴于点M ，若12PM PN =，求m 的值．【分析】（1）将A ，B ，C 三点坐标代入函数解析式即可解决问题． （2）用m 表示出PM 和PN ，建立关于m 的方程即可解决问题． 【解答】解：（1）由题知，将A ，B ，C 三点坐标代入函数解析式得，4209306a b c a b c c −+=⎧⎪++=⎨⎪=⎩，解得116a b c =−⎧⎪=⎨⎪=⎩，所以抛物线的表达式为26y x x =−++．（2）将x m =代入抛物线得表达式得，26y m m =−++， 所以点P 的坐标为2(,6)m m m −++． 令直线BC 的函数解析式为y px q =+，则306p q q +=⎧⎨=⎩，解得26p q =−⎧⎨=⎩，所以直线BC 的函数解析式为26y x =−+． 因为132m <<，且抛物线的对称轴为直线12x =，所以12PM m =−． 又因为点N 坐标为(,26)m m −+，所以226(26)3PN m m m m m =−++−−+=−+． 因为12PM PN =， 所以211(3)22m m m −=−+，解得m =， 又因为132m <<，所以m =． 【点评】本题考查待定系数法求二次函数解析式及二次函数的图象和性质，熟知待定系数法及二次函数的图象和性质是解题的关键．13．（2024•东营区校级一模）如图，在平面直角坐标系xOy 中，直线28y x =−+与抛物线2y x bx c =−++交于A ，B 两点，点B 在x 轴上，点A 在y 轴上． （1）求抛物线的函数表达式；（2）点C 是直线AB 上方抛物线上一点，过点C 分别作x 轴，y 轴的平行线，交直线AB 于点D ，E ．当38DE AB =时，求点C 的坐标．【分析】（1）根据一次函数解析式求出A ，B 两点坐标，再将A ，B 两点坐标代入二次函数解析式即可解决问题．（2）根据AOB ECD ∆∆∽得到CD 与OB 的关系，建立方程即可解决问题． 【解答】解：（1）令0x =得，8y =， 所以点A 的坐标为(0,8)； 令0y =得，4x =， 所以点B 的坐标为(4,0)；将A ，B 两点坐标代入二次函数解析式得，81640c b c =⎧⎨−++=⎩，解得28b c =⎧⎨=⎩，所以抛物线的函数表达式为228y x x =−++． （2）因为//CD x 轴，//CE y 轴， 所以AOB ECD ∆∆∽， 则CD DEOB AB=． 因为38DE AB =，4OB =， 所以32CD =． 令点C 坐标为2(,28)m m m −++， 则点D 坐标为21(2m m −，228)m m −++所以2211()222CD m m m m m =−−=−+，则213222m m −+=，解得1m =或3．当1m =时，2289m m −++=； 当3m =时，2285m m −++=； 所以点C 的坐标为(1,9)或(3,5)．【点评】本题考查待定系数法求二次函数解析式及二次函数图象上点的坐标特征，熟知待定系数法及二次函数的图象和性质是解题的关键．14．（2024•南关区校级二模）已知二次函数2y x bx c =++的图象经过点(0,3)A −，(3,0)B ．点P 在抛物线2y x bx c =++上，其横坐标为m ．（1）求抛物线的解析式；（2）当23x −<<时，求y 的取值范围；（3）当抛物线2y x bx c =++上P 、A 两点之间部分的最大值与最小值的差为34时，求m 的值； （4）点M 在抛物线2y x bx c =++上，其横坐标为1m −．过点P 作PQ y ⊥轴于点Q ，过点M 作MN x ⊥轴于点N ，分别连结PM ，PN ，QM ，当PQM ∆与PNM ∆的面积相等时，直接写出m 的值． 【分析】（1）依据题意，将A 、B 两点代入解析式求出b ，c 即可得解；（2）依据题意，结合（1）所求解析式，再配方可得抛物线的最值，进而由23x −<<可以判断得解； （3）依据题意，分类讨论计算可以得解；（4）分别写出P 、Q 、M 、N 的坐标，PQM ∆与PNM ∆的面积相等，所以Q 到PM 的距离等于N 到PM 的距离，可得m 的值．【解答】解：（1）由题意，将(0,3)A −，(3,0)B 代入解析式2y x bx c =++得，3c =−，930b c ++=，2b ∴=−，3c =−，∴抛物线的解析式为223y x x =−−；（2）由题意，抛物线2223(1)4y x x x =−−=−−，∴抛物线223y x x =−−开口向上，当1x =时，y 有最小值为4−，当2x =−时，5y =；当3x =时，0y =， ∴当23x −<<时，45y −<…；（3）由题意得，2(,23)P m m m −−，(0,3)A −，①当0m <时，P 、A 两点之间部分的最大值为223m m −−，最小值为3−， 2323(3)4m m ∴−−−−=，解得：1m =−②当02m ……时，P 、A 两点之间部分的最大值为3−，最小值为223m m −−或4−， 显然最小值是4−时不合题意， ∴最小值为223m m −−， 233(23)4m m ∴−−−−=， 解得：32m =或12m =， 32m =时，P 、A 两点之间部分的最小值为4−，故舍去， ③当2m <时，P 、A 两点之间部分的最大值为223m m −−，最小值为4−， 2323(4)4m m ∴−−−−=，解得：1m =+，12+<，故舍去，综上，满足题意得m 的值为：1或12； （4）由题意得，2(1,4)M m m −−，(1,0)N m −，2(0,23)Q m m −−， 设PM y kx b =+，代入P 、M 两点， 2223(1)4mk b m m m k b m ⎧+=−−⎨−+=−⎩， 解得：1k =−，23b m m =−−，23PM y x m m =−+−−，PQM ∆与PNM ∆的面积相等，Q ∴到23PM y x m m =−+−−的距离与N 到23PM y x m m =−+−−的距离相等，Q 到23PM y x m m =−+−−的距离=，N 到23PMy x m m =−+−−的距离=， 2|||4|m m ∴−=−+，当2m <−时，24m m −=−，解得：m =，当20m −……时，24m m −=−，解得：m =，当02m <…时，24m m =−，解得：m =当2m <时，24m m =−，解得：m =综上，满足题意得m ． 【点评】本题考查了二次函数，关键是注意分类讨论． 题型四．抛物线与x 轴的交点（共14小题）15．（2024•秦淮区校级模拟）已知函数2(2)2(y mx m x m =−−−为常数）． （1）求证：不论m 为何值，该函数的图象与x 轴总有公共点．（2）不论m ． （3）在22x −……的范围中，y 的最大值是2，直接写出m 的值． 【分析】（1）分两种情况讨论，利用判别式证明即可；（2）当1x =时，0y =，当0x =时，2y =−，即可得到定点坐标；（3）利用抛物线过两个定点，得到函数y 随x 增大而增大，代入解析式求出m 值即可． 【解答】解：（1）①当0m =时，函数解析式为22y x =−，此一次函数与x 轴有交点； ②当0m ≠时，函数解析式为2(2)2y mx m x =−−−，令0y =，则有2(2)20mx m x −−−=，△2222(2)4(2)44844(2)0m m m m m m m m =−−⨯−=−++=++=+…． ∴不论m 为何值，该函数的图象与x 轴总有公共点．（2）222(2)222()22y mx m x mx mx x m x x x =−−−=−+−=−+−， 当1x =时，0y =， 当0x =时，2y =−，∴不论m 为何值，该函数的图象经过的定点坐标是(1,0)．(0,2)−故答案为：(1,0)，(0,2)−，（3）若0m =，函数22y x =−，y 随x 增大而增大，当2x =时，2y =，与题干条件符； 当0m ≠时，函数2(2)2y mx m x =−−−是二次函数，①当0m >时，抛物线过(1,0)，(0,2)−两点，当22x −……的范围中时，y 随x 的增大而增大， ∴当2x =时，2y =，即242(2)2m m =−−−，解得0m =（舍去）．②当0m <时，抛物线过(1,0)，(0,2)−两点，其增减性依旧是y 随x 的增大而增大和①相同．综上分析，0m =．【点评】本题考查了二次函数的图象与性质，熟练掌握二次函数的性质是解答本题的关键．16．（2024•柳州模拟）如图，在平面直角坐标系中，二次函数2y x bx c =++的图象与x 轴交于A ，B 两点，B 点的坐标为(3,0)，与y 轴交于点(0,3)C −，点D 为抛物线的顶点． （1）求这个二次函数的解析式； （2）求ABD ∆的面积【分析】（1）利用待定系数法求解即可； （2）先求出点A 和点D 坐标，再根据||2D ABD AB y S ∆⋅=解析求解即可．【解答】解：（1）将(3,0)B ，(0,3)C −代入2y x bx c =++得0933b c c =++⎧⎨=−⎩，解得23b c =−⎧⎨=−⎩，∴二次函数的解析式为：223y x x =−−；（2）将223y x x =−−配方得顶点式2(1)4y x =−−， ∴顶点(1,4)D −，在223y x x =−−中，当2230y x x =−−=时， 解得1x =−或3x =， (1,0)A ∴−，4AB ∴=， ∴||44822D ABD AB y S ∆⋅⨯===． 【点评】本题主要考查了抛物线与x 轴的交点，二次函数的性质，二次函数图象上点的坐标特征，待定系数法求二次函数解析式，熟练掌握二次函数的性质是解答本题的关键．17．（2024•安阳模拟）如图，在平面直角坐标系xOy 中，抛物线2y ax bx c =++与抛物线21y x x =−+−的形状相同，且与x 轴交于点(1,0)−和(4,0)．直线2y kx =+分别与x 轴、y 轴交于点A ，B ，交抛物线2y ax bx c =++于点C ，D （点C 在点D 的左侧）． （1）求抛物线的解析式；（2）点P 是直线2y kx =+上方抛物线上的任意一点，当2k =时，求PCD ∆面积的最大值； （3）若抛物线2y ax bx c =++与线段AB 有公共点，结合函数图象请直接写出k 的取值范围．【分析】（1）根据题意直接求出二次函数解析式即可；（2）求出直线与抛物线的交点C ，D 坐标，过点P 作y 轴的平行线交CD 于点H ，交x 轴于点G ，设点P坐标为(m ，234)(12)m m m −++−<<，则点(,22)H m m +，求出PH ，由三角形的面积公式求出关于m 的函数解析式，再根据函数的性质求最值； （3）分0k >和0k <两种情况讨论即可．【解答】解：（1）抛物线2y ax bx c =++与抛物线21y x x =−+−的形状相同，1a ∴=−，抛物线2y ax bx c =++与x 轴交于点(1,0)−和(4,0)， ∴抛物线的解析式为2(1)(4)34y x x x x =−+−=−++；（2）当2k =时，联立方程组22234y x y x x =+⎧⎨=−++⎩，解得10x y =−⎧⎨=⎩或26x y =⎧⎨=⎩， (1,0)C ∴−，(2,6)D ，过点P 作y 轴的平行线交CD 于点H ，交x 轴于点G ，如图，设点P 坐标为(m ，234)(12)m m m −++−<<， ∴点(,22)H m m +，2234(22)2PH m m m m m ∴=−++−+=−++，221331273(2)()22228PCD S PH m m m ∆∴=⨯=−++=−−+， 302−<，12m −<<， ∴当12m =时，S 有最大值，最大值为278． PCD ∴∆面积的最大值为278； （3）令0x =，则2y =， ∴点B 坐标为(0,2)，令0y =，则20kx +=， 解得2x k=−，∴点A 坐标为2(k−，0)， 若抛物线2y ax bx c =++与线段AB 有公共点， 当0k >时，如图所示，则21k−<−， 解得02k <<； 当0k <时，如图所示：则24k−>， 解得102k −<<；综上所述，k 的取值范围为02k <<或102k −<<．【点评】本题考查抛物线与x 轴的交点，待定系数法求函数解析式，二次函数图象上点的坐标特征，一次函数图象上点的坐标特征，二次函数的最值等知识，关键是对这些知识的掌握和运用．18．（2024•西湖区校级模拟）已知21()y ax a b x b =+++和22()(y bx a b x a a b =+++≠且0)ab ≠是同一直角坐标系中的两条抛物线．（1）当1a =，3b =−时，求抛物线21()y ax a b x b =+++的顶点坐标； （2）判断这两条抛物线与x 轴的交点的总个数，并说明理由；（3）如果对于抛物线21()y ax a b x b =+++上的任意一点(,)P m n 均有22n a b +…．当20y …时，求自变量x 的取值范围．【分析】（1）把a ，b 的值代入配方找顶点即可解题；（2）分别令10y =，20y =，解方程求出方程的解，然后根据条件确定交点的个数即可解题；（3）现根据题意得到0a <，且24()224ab a b a b a−+=+，然后得到30b a =−>，借助图象求出不等式的解集即可．【解答】解：（1）当1a =，3b =−时，2221()23(1)4y ax a b x b x x x =+++=−−=−−， ∴顶点坐标为(1,4)−；（2）3个，理由为：令10y =，则2()0ax a b x b +++=， 即()(1)0ax b x ++=， 解得：1bx a=−，21x =−， 令20y =，则2()0bx a b x a +++=， 即()(1)0bx a x ++=， 解得：1ax b=−，21x =−， 又a b ≠且0ab ≠，∴两条抛物线与x 轴的交点总个数为3个；（3）抛物线21()y ax a b x b =+++上的任意一点(,)P m n 均有22n a b +…，0a ∴<，且24()224ab a b a b a−+=+，整理得：30b a =−>，∴22()y bx a b x a =+++的开口向上，且抛物线与x 轴交点的横坐标为113x =，21x =−， 如图所示，借助图象可知当13x …或1x −…时，20y …．【点评】本题考查二次函数的图象和性质，掌握配方法求顶点坐标，二次函数和一元二次方程的关系是解题的关键．19．（2024•三元区一模）抛物线23y ax bx =++与x 轴相交于点(1,0)A ，(3,0)B ，与y 轴正半轴相交于点C ． （1）求抛物线的解析式；（2）点1(M x ，1)y ，2(N x ，2)y 是抛物线上不同的两点． ①当1x ，2x 满足什么数量关系时，12y y =； ②若12122()x x x x +=−，求12y y −的最小值． 【分析】（1）用待定系数法即可求解；（2）①若12y y =，则M 、N 关于抛物线对称轴对称，即可求解；②22121122121212(43)(43)()()4()y y x x x x x x x x x x −=−+−−+=+−+−，而12122()x x x x +=−，得到12y y −的函数表达式，进而求解．【解答】解：（1）设抛物线的表达式为：12()()y a x x x x =−−， 即2(1)(3)(43)y a x x a x x =−−=−+， 即33a =， 解得：1a =，故抛物线的表达式为：243y x x =−+；（2）如图，。

2023年九年级中考数学复习：二次函数（特殊四边形问题）综合题1．已知抛物线()21=++4(0)2y a x m m am -≠过点()0,4A(1)若=2m ，求a 的值；(2)如图，顶点M 在第一象限内，B 、C 是抛物线对称轴l 上的两点，且MB MC =，在直线l 右侧以BC 为边作正方形BCDE ，点E 恰好在抛物线上．①求am 的值；①试判断点E 和点A 是否关于直线l 对称，如果对称，请说明理由，如果不对称，请举出反例．2．如图，抛物线y ＝ax 2-2x +c (a ≠0)与直线y ＝x +3交于A ，C 两点，与x 轴交于点B ．（1）求抛物线的解析式．（2）点P 是抛物线上一动点，且在直线AC 下方，当①ACP 的面积为6时，求点P 的坐标．（3）D 为抛物线上一点，E 为抛物线的对称轴上一点，请直接写出以A ，C ，D ，E 为顶点的四边形为平行四边形时点D 的坐标．3．如图1，二次函数y ＝ax 2+bx +c （a ≠0）的图象与x 轴交于A （﹣1，0）、B （3，0），与y 轴交于点C ，连接AC 和BC ，①OAC ＝60°．（1）求二次函数的表达式．（2）如图2，线段BC 上有M 、N 两动点（N 在M 上方），且MN 3P 是直线BC 下方抛物线上一动点，连接PC 、PB ，当①PBC 面积最大时，连接PM 、AN ，当MN 运动到某一位置时，PM +MN +NA 的值最小，求出该最小值．（3）如图3，在（2）的条件下，连接AP ，将AP 绕着点A 逆时针旋转60°至AQ ．点E 为二次函数对称轴上一动点，点F 为平面内任意一点，是否存在这样的点E 、F ，使得四边形AEFQ 为菱形，若存在，请直接写出点E 的坐标，若不存在，请说明理由．4．直线3y x =-+与x 轴相交于点A ，与y 轴相交于点B ，抛物线2y ax 2x c =++经过点A ，B ，与x 轴的另一个交点为C ．（1）求抛物线的解析式；（2）如图1，若点P为直线AB上方的抛物线上的一动点，求四边形APBO的面积的最大值；D为抛物线上的一点，直线CD与AB相交于点M，点H在抛物线上，（3）如图2，(2,3)∥轴，交直线CD于点K．P是平面内一点，当以点M，H，K，P为顶点的四过H作HK y边形是正方形时，请直接写出点P的坐标．5．综合与探究如图1所示，直线y=x+c与x轴交于点A（-4，0），与y轴交于点C，抛物线y=-x2+bx+c经过点A，C．（1）求抛物线的解析式；（2）点E在抛物线的对称轴上，求CE+OE的最小值为______．（3）如图2所示，M是线段OA的上一个动点，过点M垂直于x轴的直线与直线AC和抛物线分别交于点P、N①当ANC面积最大时的P点坐标为______；最大面积为______．①点F是直线AC上一个动点，在坐标平面内是否存在点D，使以点D、F、B、C为顶点的四边形是菱形？若存在，请直接写出点D的坐标；若不存在，请说明理由．。

2023年九年级中考数学复习：二次函数综合题（特殊三角形问题）1．抛物线y＝ax2＋c交x轴于A、B（1，0）两点，且经过（2，3）．(1)求抛物线的解析式；(2)如图1，直线y＝kx＋3交y轴于点G，交抛物线y＝ax2＋c于点E和F，F在y轴右侧，若△GOF的面积为△GOE面积的2倍，求k值；(3)如图2，点P是第二象限的动点，分别连接P A、PB，并延长交直线y=－2于M、N 两点. 若M、N两点的横坐标分别为m、n，试探究m、n之间的数量关系．2．如图，已知抛物线2=++与直线y=0.5x＋3相交于A，B两点，交△轴于C，0.5y x bx cD两点，连接AC，BC，已知A（0，3），C（－3，0）.(1)求抛物线的表达式；(2)在抛物线对称轴l上找一点M，使|MB一MD|的值最大，并求出这个最大值；(3)点P为y轴右侧抛物线上的一动点，连接P A，过点P作PQ△P A交y轴于点Q，是否存在点P，使得以A，P，Q为顶点的三角形与△ABC相似？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由.3．如图，抛物线与x轴交于A和B两点（点B位于点A右侧），与y轴交于点C，对称轴是直线x=2，且OA=1，OC=3，连接AC，BC．(1)求此抛物线的函数解析式；(2)设抛物线的顶点为点P，请在x轴上找到一个点D，使以点P、B、D为顶点的三角形与△ABC相似？(3)此抛物线的对称轴和以AC为直径的圆是什么位置关系？如果是相切或相交，请直接写出切点或交点的坐标（不必写演推过程）；如果是相离，请简要说明理由．4．如图1，已知抛物线y=ax2+bx+3与x轴分别交于A(−3，0)，B(1，0)两点，与y轴交于点C，点D为抛物线的顶点，连接AD、CD、AC、BC．(1)请直接写出抛物线的表达式及顶点D的坐标；(2)求证：△ACD是直角三角形；(3)判断△ACB和△OAD的数量关系，并说明理由；(4)如图2，点F是线段AD上一个动点，以A，F，O为顶点的三角形是否与△ABC相似？若相似，请直接写出点F的坐标；若不相似，请说明理由．5．抛物线y＝ax2﹣2x+c经过点A(3，0)，点C(0，﹣3)，直线y＝﹣x+b经过点A，交抛物线于点E．抛物线的对称轴交AE于点B，交x轴于点D，交直线AC于点F．(1)求抛物线的解析式；(2)如图△，点P 为直线AC 下方抛物线上的点，连接P A ，PC ，△BAF 的面积记为S 1，△P AC 的面积记为S 2，当S 2＝38S 1时．求点P 的横坐标；(3)如图△，连接CD ，点Q 为平面内直线AE 下方的点，以点Q ，A ，E 为顶点的三角形与△CDF 相似时（AE 与CD 不是对应边），请直接写出符合条件的点Q 的坐标． 6．如图，抛物线23y ax bx =+-与x 轴交于点()1,0A 、()3,0B ，与y 轴交于点C ，联结AC 、BC ．(1)求该抛物线的表达式及顶点D 的坐标；(2)如果点P 在抛物线上，CB 平分ACP ∠，求点P 的坐标：(3)如果点Q 在抛物线的对称轴上，DBQ 与ABC 相似．求点Q 的坐标．7．如图1，已知二次函数y ＝ax2＋bx ＋c （a ≠0）的图象与x 轴交于A （﹣1，0），B （3，0）两点，与y 轴交于点C （0，﹣2），顶点为D ，对称轴交x 轴于点E ．(1)求该二次函数的解析式；(2)设M 为该抛物线上直线BC 下方一点，过点M 作x 轴的垂线，交线段BC 于点N ，线段MN 是否存在最大值？若存在，请求出其最大值；若不存在，请说明理由；(3)连接CE （如图2），设点P 是位于对称轴右侧该抛物线上一点，过点P 作PQ △x 轴，垂足为Q ．连接PE ，请求出当△PQE 与△COE 相似时点P 的横坐标．8．如图，直线y kx b =+与x 轴、y 轴分别交于A ，B 两点，抛物线2y ax bx c =++经过A ，B 两点，点C 的坐标为()1,0-，3AO CO ==，点C 关于点B 的对称点M 刚好落在抛物线上，连接AM ．(1)求点M 的坐标；(2)求抛物线的解析式；(3)过点M 作MD 平行于y 轴交AB 于点D ，若点E 为抛物线上的一点，点F 在x 轴上，连接AE ，AF ，EF ．是否存在点F 使得△ADM 与△AEF 相似？若存在，请直接写出点F 的坐标；若不存在，请说明理由．9．如图1，已知在平面直角坐标系xOy 中，四边形OABC 是边长为3的正方形，其中顶点A ，C 分别在x 轴的正半轴和y 轴的正半轴上，抛物线2y x bx c =-++经过A ，C 两点，与x 轴交于另一个点D ．(1)△求点A ，B ，C 的坐标；△求b ，c 的值．(2)若点P 是边BC 上的一个动点，连结AP ，过点P 作PM △AP ，交y 轴于点M （如图2所示）．当点P 在BC 上运动时，点M 也随之运动．设BP ＝m ，CM ＝n ，试用含m 的代数式表示n ，并求出n 的最大值．10．平面直角坐标系中，已知抛物线1C ：()21y x m x m =-++-（m 为常数）与x 轴交于点A ，B 两点（点A 在点B 左边），与y 轴交于点C ．(1)若4m =，求点A ，B ，C 的坐标；(2)如图1，在（1）的条件下，D 为抛物线x 轴上方一点，连接BD ，若90DBA ACB ∠∠+=︒，求点D 的坐标；(3)如图2，将抛物线1C 向左平移n 个单位长度（0n >）与直线AC 交于M ，N （点M 在点N 右边），若2AM CN =，求m ，n 之间的数量关系．11．如图，直线y x n =-+与x 轴交于点()3,0A ，与y 轴交于点B ，抛物线2y x bx c =-++经过点A ，B ．(1)求n 的值及抛物线的解析式；(2)(),0E m 为x 轴上一动点，过点E 作ED x ⊥轴，交直线AB 于点D ，交抛物线于点P ，连接BP ．△点E 在线段OA 上运动，若BPD △与ADE 相似，求点E 的坐标；△若抛物线的顶点为Q ，AQ 与CB 的延长线交于点H ，点E 在x 轴的正半轴上运动，若PBD CBO H ∠+∠=∠．请求写出m 的值．12．如图1，平面直角坐标系xOy 中，直线y ＝－12x －2与x 轴交于点A ，与y 轴交于点C ．抛物线y ＝14x 2＋bx ＋c 经过点A 、点C ，且与x 轴交于另一点B ，连接BC ．(1)求抛物线的解析式；(2)点P 是抛物线上一动点．△当点P 在直线AC 下方的抛物线上运动时，如图2，连接AP ，CP ．求四边形ABCP 面积的最大值及此时点P 的坐标；△当点P 在x 轴上方的抛物线上运动时，过点P 作PM △x 轴于点M ，连接BP ．是否存在点P ，使△PMB 与△AOC 相似？若存在，请直接写出点P 的坐标；若不存在，请说明理由．13．如图，抛物线y 2b c x ++与x 轴交于点A 、B ，点A 、B 分别位于原点的左、右两侧，BO ＝3AO ＝3，过点B 的直线与y 轴正半轴和抛物线的交点分别为C 、D ，BC．(1)求b、c的值；(2)求直线BD的直线解析式；(3)点P在抛物线的对称轴上且在x轴下方，点Q在射线BA上．当△ABD与△BPQ相似时，请直接写出所有满足条件的点Q的坐标．14．如图，抛物线23(0)y ax bx a=+-≠的顶点E的横坐标为1，与x轴交于A、B两点，与y轴交于点C，直线113y x=-+过点B，与y轴交于点D．(1)求抛物线的解析式；(2)证明：ABD CBE∠=∠；(3)是否存在点1O，使点1O到A，B，C，D的距离都相等，若存在，求出点1O坐标，若不存在，请说明理由．(4)设抛物线与直线DB另一交点为Q，F为线段BQ上一点（不含端点），连接AF，一动点P从点A出发，沿线段AF以每秒1个单位的速度运动到F，再沿线段FQ个单位的速度运动到Q后停止，当点F的坐标是多少时，点P在整个运动过程中用时最少？（直接写出答案）15．如图，在平面直角坐标系中，抛物线y ＝ax 2+bx +c （a ≠0）与x 轴交于点A 、B ，与y 轴交于点C ，且OC ＝2OB ＝6OA ＝6，点P 是第一象限内抛物线上的动点．(1)求抛物线的解析式；(2)连接BC 与OP ，交于点D ，当PD ：OD 的值最大时，求点P 的坐标；(3)点P 在抛物线上运动，点N 在y 轴上运动，是否存在点P 、点N ．使△CPN ＝90°，且△CPN 与△BOC 相似，若存在，请直接写出点P 的坐标，若不存在，说明理由．16．在平面直角坐标系xOy 中，抛物线y ＝﹣x 2+bx +c 与x 轴分别交于点A ，点B （3，0），与y 轴交于点C （0，3）．(1)求抛物线的解析式；(2)如图1，连接BC ，点D 是直线BC 上方抛物线上一动点，连接AD 交BC 于点E ，若AE ＝2ED ，求点D 的坐标；(3)直线y ＝kx ﹣2k +1与抛物线交于M ，N 两点，取点P （2，0），连接PM ，PN ，求△PMN 面积的最小值．17．综合与探究如图，直线3y x =-+与x 轴，y 轴分别交于B ，C 两点，抛物线2y x bx c =-++经过点B ，C ，与x 轴的另一交点为A ，顶点为D ．(1)求抛物线的解析式及顶点D的坐标．(2)连接CD，BD，求点D到BC的距离h．(3)P为对称轴上一点，在抛物线上是否存在点Q，使得PDQ与BOC相似？若存在，请直接写出Q点坐标；若不存在，请说明理由．18．如图，已知直线223y x=-与x轴交于点A，与y轴交于点B，抛物线226y x bx=-++经过点A，与x轴的另一个交点为C，交y轴于点D．(1)求抛物线的函数表达式及点D的坐标；(2)点M是y轴上的点，在y轴右侧的抛物线上是否存在点P，使得PMD△与BOC相似，且点M与点O为对应点，若存在，请求出点P的坐标，若不存在，请说明理由．19．如图，在平面直角坐标系中，直线y=2x+6与x轴交于点A，与y轴交点C，抛物线y=-2x2+bx+c过A，C两点，与x轴交于另点B．(1)求抛物线的解析式．(2)在直线AC 上方的抛物线上有一动点E ，连接BE ，与直线AC 相交于点F ，当EF =12BF 时，求sin△EBA 的值．(3)点N 是抛物线对称轴上一点，在(2)的条件下，若点E 位于对称轴左侧，在抛物线上是否存在一点M ，使以M ，N ，E ，B 为顶点的四边形是平行四边形？若存在，直接写出点M 的坐标；若不存在，请说明理由．20．如图，一次函数3y x =-+的图象与x 轴和y 轴分别交于点B 和点C ，二次函数2y x bx c =-++的图象经过B ，C 两点，并与x 轴交于点A ．点(),0M m 是线段OB 上一个动点（不与点O 、B 重合），过点M 作x 轴的垂线，分别与二次函数图象和直线BC 相交于点D 和点E ，连接CD ．(1)求这个二次函数的解析式．(2)△求DE 、CE 的值（用含m 的代数式表示）．△当以C ，D ，E 为顶点的三角形与△ABC 相似时，求m 的值．(3)点F 是平面内一点，是否存在以C ，D ，E ，F 为顶点的四边形为菱形？若存在，请直接写出点M 的坐标；若不存在，请说明理由．参考答案：1．(1)21y x =- (2)k =(3) 1.-2．(1)215322y x x =++(3)在点P （1，6）3．(1)y =x 2－4x +3(2)点D 的坐标是（0，0）或（73，0） (3)相交，交点的坐标是（2，1）或（2，2）4．(1)抛物线解析式为y =-x 2-2x +3；顶点D 的坐标为（-1，4）；(2)见解析(3)△OAD =△ACB(4)相似，F 点的坐标为（-65，185）或（-2，2）．5．(1)y ＝x 2﹣2x ﹣3(2)P 352(3)Q 点坐标为(﹣7，5)或(﹣12，5)或(3，﹣10)或(3，﹣5)6．(1)2=+43y x x --，(21)D ， (2)111639⎛⎫ ⎪⎝⎭，- (3)(2，−2)或12,3⎛⎫ ⎪⎝⎭7．(1)224233y x x =--(2)线段MN 存在最大值，最大值为32(3)点P 的横坐标为5或28．(1)(M(2)2y x x =(3)存在，()()()()()11,0,3,0,,0,5,0,7,0,13,03⎛⎫-- ⎪⎝⎭9．(1)△A (3，0)，B (3，3)，C (0，3)；△23b c =⎧⎨=⎩ (2)2133324n m ⎛⎫=--+ ⎪⎝⎭（0≤m ≤3）；3410．(1)A （1，0），B （4，0），C （0，﹣4）(2)D （83，209） (3)93m n =-11．(1)n =3，y =-x 2+2x +3．(2)△（1，0）或（2，0）．△m =5或73．12．(1)211242y x x =+- (2)△四边形ABCP 面积的最大值为8，此时点P 为（－2，－2）；△存在符合条件的点P ，点P 坐标为（－6，4）或（－12，28）或（4，4）13．(1)132b c ⎧=-⎪⎪⎨⎪=-⎪⎩(2)y=+(3)Q 1（，0）、Q 2（0）、Q 3，0）、Q 4（，0） 14．(1)2 2 3y x x =--(2)见解析(3)存在点()111O -,，使点P 到A ，B ，C ，D 的距离都相等(4)F 的坐标为41,3⎛⎫- ⎪⎝⎭时，点P 在整个运动过程中用时最少15．(1)y ＝﹣2x 2+4x +6(2)点P 的坐标为315(,)22(3)存在，点P 的坐标分别为(3，0)或(1，8)或939(,)48或755(,)4816．(1)y ＝﹣x 2+2x +3(2)（1，4）或（2，3）17．(1)223y x x =-++，顶点D (1，4)(2)h =(3)Q （0，3）或（2，3）18．(1)2246y x x =-++；(0,6)D(2)存在，点P 的坐标为755,48⎛⎫ ⎪⎝⎭或939,48⎛⎫ ⎪⎝⎭或(1,8)或(3,0)19．(1)抛物线的解析式为y =-2x 2-4x +6；(2)sin△EBA ； (3)M 的坐标为（2，-10）或（-4，-10）或（0，6）．20．(1)223y x x =-++(2)△23DE m m =-，CE ；△m 的值为32或53(3)存在以C ，D ，E ，F 为顶点的四边形为菱形，点M 的坐标为(1，0)或(2，0)或(3，0)．。

2023年九年级数学中考专题：二次函数综合压轴题（特殊三角形问题）1．在平面直角坐标系中，由两条与x 轴有着相同的交点，并且开口方向相同的抛物线所围成的封闭曲线称为“月牙线”．如图所示，抛物线1C 与抛物线2C ：()24120y mx mx m m =+->组成一个“月牙线”，相同的交点分别为M ，N （点M 在点N 的左侧），与y 轴的交点分别为A ，B ，且点A 的坐标为()0,1-．(1)求M ，N 两点的坐标及抛物线1C 的解析式；(2)若抛物线2C 的顶点为D ，当34m =时，试判断三角形MND 的形状，并说明理由；(3)在（2）的条件下，点5,4P t ⎛⎫- ⎪⎝⎭是抛物线1C 上一点，抛物线2C 第三象限上是否存在一点Q ，使得32APM ONQ S S =△△，若存在，请直接写出点Q 的坐标；若不存在，说明理由．2．如图，在平面直角坐标系中，点A ，B 分别是y 轴正半轴，x 轴正半轴上两动点，2OA k =，23OB k =+，以AO ，BO 为邻边构造矩形AOBC ，抛物线2334y x x k =-++交y 轴于点D ，P 为顶点，PM x ⊥轴于点M ．(1)求OD ，PM 的长（结果均用含k 的代数式表示）． (2)当PM BM =时，求该抛物线的表达式．(3)在点A 在整个运动过程中，若存在ADP △是等腰三角形，请求出所有满足条件的k 的值．3．如图1，抛物线211384y x x =--与x 轴交于A B 、两点（点A 在点B 的左侧），与y 轴交于点C ．点D 在y轴正半轴上，直线AD ：y x b =+与抛物线交于点E ．(1)求线段BC 的长度；(2)如图2，点Р是线段AE 上的动点，过点P 作y 轴的平行线交抛物线于点Q ，求PQCD的最大值； (3)如图3，将抛物线211384y x x =--向左平移4个单位长度，将DCA △沿直线BC 平移，平移后的DCA △记为D C A '''△，在新抛物线的对称轴上找一点M ，当A C M ''△是以点A '为直角顶点的等腰直角三角形时，请直接写出所有符合条件的点M 的坐标．4．如图1，抛物线2y ax 2x c =++经过点(1,0)A -、(0,3)C ，并交x 轴于另一点B ，点(,)P x y 在第一象限的抛物线上，AP 交直线BC 于点D ．(1)求该抛物线的函数表达式；(2)如图1，当点P 的坐标为(1,4)时，求四边形BOCP 的面积； (3)请利用备用图，若点Q 也是抛物线上的一点， ①当PDAD的值最大时，求此时点P 的坐标； ②当PDAD的值最大且APQ △是直角三角形时，求点Q 的横坐标．5．如图，抛物线22y ax bx =++经过点()()1040A B -，，，，交y 轴于点C ．(1)求抛物线的顶点坐标；(2)点D 为抛物线上一点，是否存在点D 使23ABCABDS S =，若存在请直接给出点D 坐标；若不存在请说明理由；(3)将直线BC 绕点B 顺时针旋转45°，与抛物线交于另一点E ，求直线BE 的解析式．6．已知抛物线2y x bx c =-++经过()1,0A -、()0,3B 两点，O 为坐标原点，抛物线交正方形OBDC 的边BD 于点E ，点M 为射线BD 上一动点，连接OM ，交BC 于点F ．(1)求b 和c 的值及点C 的坐标； (2)求证∶BOF BDF ∠=∠(3)是否存在点M ，使MDF △为等腰三角形？若不存在，请说明理由；若存在，求ME 的长．7．在平面直角坐标系中，正方形ABCD 的顶点A 在y 轴上，顶点B 在x 轴上，OA 、OB 的长分别是一元二次方程214480x x -+=的两个根（OA OB >）．(1)求A 、B 两点坐标；(2)二次函数2y x bx c =++经过点A 和点D ，求此二次函数解析式；(3)在直线BC 上是否存在点P ，使PCD 为等腰三角形？若存在，请直接写出点P 的坐标；若不存在，说明理由．8．如图①，抛物线2169y ax x c =++，与x 轴交于A ，B 两点（A 在B 的左边），与y 轴交于C 点，顶点为E ，其中，点A 坐标为(1,0)-，对称轴为2x =．(1)求此抛物线解析式；(2)在第四象限的抛物线上找一点F ，使FBC ACB S S =△△，求点F 的坐标；(3)如图②，点P 是x 轴上一点，点E 与点H 关于点P 成中心对称，点B 与点Q 关于点P 成中心对称，当以点Q ，H ，E 为顶点三角形是直角三角形时，求P 的坐标．9．如图，抛物线2y ax bx c =++经过()1,0A -、()3,0B 、()0,3C 三点，直线l 是抛物线的对称轴．(1)求抛物线的函数关系式：(2)设点P 是直线l 上的一个动点，当PAC △的周长最小时，求点P 的坐标：(3)在直线l 上是否存在点M ，使MAC △为等腰三角形，若存在，直接写出所有符合条件的点M 的坐标；若不存在，请说明理由；(4)若点E 在x 轴上，点F 在抛物线上，是否存在以B ，C ，E ，F 为顶点且以BC 为一边的平行四边形？若存在，求点F 的坐标：若不存在，请说明理由．10．如图，在平面直角坐标系中，点O 为坐标原点，二次函数()230y ax bx a a =+-<的图象与x 轴交于A 、B （点A 在点B 左侧）两点，与y 轴交于点C ，已知点()3,0B ，P 点为抛物线的顶点，连接PC ，作直线BC ．(1)点A 的坐标为 ；(2)若射线CB 平分PCO ∠，求二次函数的表达式；(3)在（2）的条件下，如果点(),0D m 是线段AB （含A 、B ）上一个动点，过点D 作x 轴的垂线，分别交直线BC 和抛物线于E 、F 两点，当m 为何值时，CEF △为直角三角形？11．如图，已知抛物线2y x mx n =-++与x 轴交于A 、B 两点，与y 轴交于点C ，抛物线的对称轴交x 轴于点D ，已知()10A -，，()03C ，．(1)求抛物线的表达式；(2)在抛物线的对称轴上是否存在点P，使PCD是以CD为腰的等腰三角形？如果存在，直接写出P点的坐标；如果不存在，请说明理由；(3)点E是线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDBF的面积最大？求出四边形CDBF的最大面积及此时E点的坐标．12．如图，抛物线y＝ax2＋bx过A（4，0），B（1，3）两点，点C、B关于抛物线的对称轴对称，过点B 作直线BH⊥x轴，交x轴于点H．(1)求抛物线的表达式；(2)直接写出点C的坐标，并求出△ABC的面积；(3)若点M在直线BH上运动，点N在x轴上运动，是否存在以点C、M、N为顶点的三角形为等腰直角三角形？若存在，求出其值；若不存在，请说明理由．13．如图，抛物线y＝ax2＋bx＋2交x轴于点A（﹣3，0）和点B（1，0），交y轴于点C．已知点D的坐标为（﹣1，0），点P为第二象限内抛物线上的一个动点，连接AP、PC、CD．(1)求这个抛物线的表达式．(2)点P 为第二象限内抛物线上的一个动点，求四边形ADCP 面积的最大值．(3)①点M 在平面内，当△CDM 是以CM 为斜边的等腰直角三角形时，求出满足条件的所有点M 的坐标； ②在①的条件下，点N 在抛物线对称轴上，当∠MNC ＝45°时，求出满足条件的所有点N 的坐标． 14．如图1，抛物线y ＝ax 2＋bx ＋3过点A （﹣1，0），点B （3，0），与y 轴交于点C ．M 是抛物线任意一点，过点M 作直线l ⊥x 轴，交x 轴于点E ，设M 的横坐标为m （0＜m ＜3）．(1)求抛物线的解析式及tan ∠OBC 的值；(2)当m ＝1时，P 是直线l 上的点且在第一象限内，若△ACP 是直角三角形时，求点P 的坐标；(3)如图2，连接BC ，连接AM 交y 轴于点N ，交BC 于点D ，连接BM ，设△BDM 的面积为S 1，△CDN 的面积为S 2，求S 1﹣S 2的最大值．15．如图，抛物线2y ax bx c =++与x 轴交于A ，B 两点，与y 轴交于点C ，已知抛物线的对称轴是直线=1x -，2OA OC ==．P 为抛物线上的一个动点，过点P 作PD x ⊥轴于点D ，交直线BC 于点E ．(1)求抛物线的函数表达式；(2)若点P在第三象限内，且14PE OD=，求PBE∆的面积．(3)在（2）的条件下，若M为直线BC上一点，是否存在点M，使BDM∆为等腰三角形？若存在，求出点M 的坐标；若不存在，请说明理由．16．二次函数y＝ax2+bx+2的图象交x轴于点A(﹣1，0)，B(4，0)两点，交y轴于点C．动点M从点A出发，以每秒2个单位长度的速度沿AB方向运动，过点M作MN⊥x轴交直线BC于点N，交抛物线于点D，连接AC，设运动的时间为t秒．(1)求二次函数y＝ax2+bx+2的表达式；(2)连接BD，当t32=时，求△DNB的面积；(3)在直线MN上存在一点P，当△PBC是以∠BPC为直角的等腰直角三角形时，求此时点D的坐标；(4)当t54=时，在直线MN上存在一点Q，使得∠AQC+∠OAC＝90°，求点Q的坐标．17．如图1，抛物线y2+bx+c与x轴交于A、B两点，点A、B分别位于原点左、右两侧，且AO＝2BO ＝4，过A点的直线y＝kx+c交y轴于点C．(1)求k、b、c的值；(2)在抛物线的对称轴上是否存在一点P，使△ACP为直角三角形？若存在，直接写出所有满足条件的点的坐标；若不存在，请说明理由；(3)如图2，点M为线段AC上一点，连接OM，求1AM+OM的最小值．218．如图，已知直线y＝﹣2x+m与抛物线y＝ax2+bx+c相交于A，B两点，且点A(1，4)为抛物线的顶点，点B在x轴正方向上．(1)求抛物线的解析式；(2)若点P在抛物线第三象限的图象上，且到x轴、y轴的距离相等，①证明：POB≌POC；②直接写出OP的长；(3)若点Q是y轴上一点，且ABQ为直角三角形，求点Q的坐标．参考答案：1．(1)(6,0),(2,0)M N -，21(412)12y x x =+- (2)MND 是等腰三角形(3)存在，5(2,)6-或3(2,)2-2．(1)OD k =，3PM k =+ (2)23324y x x =-++(3)136k =或6k =或k =3．(1)(2)8156(3)()3,3-或(3,2)--4．(1)223y x x =-++ (2)152(3)①35,24P ⎛⎫⎪⎝⎭②113或1或52或765．(1)（32，258）(2)存在，共四个点，()13，或()23，或()23--，或()53-， (3)312y x =-+6．(1)2b =，3c =，()3,0C(3)存在，2或27．(1)()0,8A ，()6,0B (2)22984y x x =-+ (3)存在，()6,0P 或()22,128．(1)抛物线的解析式为241620999y x x =-++ (2)F 坐标为286,9⎛⎫- ⎪⎝⎭ (3)点P 坐标为5,06⎛⎫ ⎪⎝⎭或10,03⎛⎫- ⎪⎝⎭9．(1)223y x x =-++(2)()1,2(3)存在，点M 的坐标为(或(1,或()1,1或()1,0(4)存在，点F 的坐标为()2,3或)1,3-或()1,3-10．(1)()1,0-(2)2=+y x (3)当2m =或1-时，CEF △为直角三角形11．(1)223y x x =-++(2)存在；()1,6，(，(1, (3)518，33,22E ⎛⎫ ⎪⎝⎭12．(1)y ＝﹣x 2+4x(2)3(3)存在，N 点坐标为（2，0）或（﹣4，0）或（﹣2，0）或（4，0）13．(1)224233y x x =--+ (2)174(3)点N 的坐标为（﹣111，5）14．(1)y ＝﹣x 2+2x +3，1(2)（1，1）或（1，2）或（1，83） (3)813215．(1)211242y x x =+- (2)38(3)71,24⎛⎫-- ⎪⎝⎭或⎝⎭或⎝⎭或124,55⎛⎫-- ⎪⎝⎭16．(1)y 12=-x 232+x +2(2)2(3)D (1，3)或D (3，2)(4)Q 点坐标分别为(32，52-)，(32，52)17．(1)k ＝﹣2，b 2，c ＝﹣(2)存在，点P 的坐标为（﹣1，）或（﹣111，﹣(3)12AM +OM 18．(1)223y x x ++＝﹣(2)②OP =(3)Q (0，3.5)或Q (0，﹣1.5)或Q (0，1)或Q (0，3)。

九年级数学二次函数的图像解答题10道题专题训练学校: ____________ 姓名：_____________ 班级： ____________ 考号：_____________一、解答题1.如图，在平面直角坐标系中，二次函数的图像交坐标轴于A （-1, 0）、B （4, 0）、C（0, -4）三点，点P是直线BC下方抛物线上的一动点.（2）是否存在点P,使APOC是以OC为底边的等腰三角形？若存在，求出P点坐标; 若不存在，请说明理由；（3）动点P运动到什么位置时，四边形PBOC面积最大？求出此时点P坐标和四边形PBOC的最大面积.2.如图，二次函数y^-x^+bx + c的图像经过M（0,3）, N（—2,—5）两点.（1）求该函数的解析式；（2）若该二次函数图像与x轴交于A、B两点，求的面积；（3）若点P在二次函数图像的对称轴上，当AMNP周长最短时，求点P的坐标.3.已知二次函数y = "（X - D（x-3）（ a〉0）的图像与x轴交于A、B两点（A左B右）, 与y轴交于C点(0, 3) .P为x轴下方二次函数y = a(x - 1)(尢-3) (a > 0)图像上一点，P点横坐标为加.(1)求a的值；(2)若P为二次函数y = a(x —l)(x —3) (a > 0)图像的顶点，求证：ZAC0=ZPCB;(3)Q ("7 + ",)'o)为二次函数歹=a(x - 1)0-3) (a > 0)图像上一点，且ZAC0 = ZQCB,求n的取值范围.4.如图，已知二次函数yi=ax2+bx + c的图像经过点4(—1,0), C(0,3),且对称轴为直线x = -2, 一次函数y2 =mx + n的图像经过4』两点.(2)若点5C关于抛物线的对称轴对称，根据图像直接写出满足^>y2时x的取值范围.5.已知如图，二次函数y="ax2"+bx+c的图像过A、B、C三点观察图像写出A、B、C三点的坐标求出二次函数的解析式6.已知二次函数y = -x2 +(m-2)x + 3(m + l)的图像如图所示.(1)当mM -4时，说明这个二次函数的图像与x轴必有两个交点;(2)如图情况下，若OAOB = 6,求点C的坐标.(1)求这个二次函数的解析式；(2)观察图像，直接写出：何时y随x的增大而增大？何时y<0?&已知二次函数的图像如图所示.(1)求这个二次函数的表达式；(2)观察图像，当-2<x< 1时，写出y的取值范围.9.如图，已知二次函数y=ax2+bx+3的图像经过点A (1, 0) , B (—2, 3).(1)求该二次函数的表达式；(2)求该二次函数的最大值；(3)结合图像，解答问题：当y>3时，x的取值范围是___________ .与y轴交于C点.(1)求A、8两点的坐标：(2)若P(m,-2)为二次函数y = x2-x-2图像上一点，求加的值.参考答案1. (1) y1=x2-3x-4； (2)存在满足条件的P点，其坐标为(3上価、_2)； (3) 16.2【解析】【分析】(1)由A、B、C三点的坐标，利用待定系数法可求得抛物线解析式；(2)由题意可知点P在线段OC的垂直平分线上，则可求得P点纵坐标，代入抛物线解析式可求得P点坐标；(3)过P作PE丄x轴，交x轴于点E,交直线BC于点F,用P点坐标可表示出PF的长, 则可表示出四边形PBOC的面积，利用二次函数的性质可求得四边形PBOC面积的最大值及P点的坐标【详解】解：(1)设抛物线解析式为y=ax2+bx+c,把A、B、C三点坐标代入可得a-b+c=O< 16a + 4b + c = 0 ,c = —4a = 1解得b = —3,c =-4抛物线解析式为y=x2-3x-4；(2)作OC的垂直平分线DP,交OC于点D,交BC下方抛物线于点P,如图2,,-.PO=PC,此时P点即为满足条件的点,VC (0, -4),.•.D (0,-2),•°.P点纵坐标为-2,代入抛物线解析式可得x2-3x-4=-2,解得x上也(小于0,舍去)或x= 土位，2 2•••存在满足条件的P点，其坐标为(土戸，-2).2(3)•.•点P在抛物线上，可设P (t, t2-3t-4),过P作PE丄x轴于点E,交直线BC于点F,如图1,VB (4, 0), C (0, -4),直线BC解析式为y=x-4,.•.F (t, t-4),.•.PF= (t-4) - (t2-3t-4) =-t2+4t,• • S四边形PBOC = BCO = S pre + S PFB + S BCO=—PF«OE+ — PF«BE+ — xOC«BO= — PF(OE+BE)+ — x4x42 2 2 2 2 =丄PF9B+8 =丄(屮+盘)x4+8=-2 (t-2) 2+16,2 2.•.当t=2时，S㈣边形FBOC最大值为16,此时t2-3t-4=-6,.•.当P点坐标为(2,-6)时，四边形PBOC的最大面积为16.【点睛】本题为二次函数的综合应用，涉及待定系数法、二次函数的性质、三角形的面积、方程思想等知识.在(1)中注意待定系数法的应用，在(2)中确定出P点的位置是解题的关键，在(3)中用P点坐标表示出四边形PBOC的面积是解题的关键.2. (1) y = -x2 +2x + 3 ； (2) 6； (3) P(l,l)【解析】【分析】(1)将M,N两点代入y = -.X2 + bx + c求出be值，即可确定表达式；(2)令y=0求x的值，即可确定A、B两点的坐标，求线段AB长，由三角形面积公式求解.(3)求出抛物线的对称轴，确定M关于对称轴的对称点G的坐标，直线NG与对称轴的交点即为所求P点，利用一次函数求出P点坐标.【详解】解：将点M(0,3)> N(-2,-5)代入y--x2+bx+c中得,1 = 3_4 - 2b + c = -5，b = 2解得，°，c = 3Ay与x之间的函数关系式为y = -x2 + 2x + 3；(2)如图，当y=0时，一干+2兀+ 3 = 0，.*.X1=3,X2= -1,・・・A(・l,0),B(3,0),・・・AB=4,1 o AS A ABM=— X4X3 = 6 .2即AAW 的面积是6.答案第3页，总11页(3)如图，抛物线的对称轴为直线% = - —= = 1 ,2a -2点M(0,3)关于直线x=l的对称点坐标为G(2, 3),.•.PM=PG,连MG交抛物线对称轴于点P,此时NP+PM=NP+PG最小，即AMNP周长最短.设直线NG的表达式为y=mx+n,将N(-2,-5),G(2,3)代入得，—2m+n = —52m+n=3m = 2解得，\ ° ,n = -ly=2m-l,・・・P点坐标为(1,1).【点睛】本题考查抛物线与图形的综合题，涉及待定系数法求解析式，图象的交点问题，利用对称性解决线段和的最小值问题，利用函数观点解决图形问题是解答此题的关键.如图，二次函数y=-x2 +bx+c的图像经过M(0,3), N(-2,-5炳点.3.(1) 1； (2)证明见解析；(3) -1<77<1 ^|<n< |【解析】试题分析：⑴把点C (0, 3)代Ay = a(x - l)(x - 3) (a > 0)即可求出a=l;(2)求出点P的坐标，再求出CP=2苗，BP=<2, CB=3近,判断出ABCP为直角三角形, 通过解直角三角形，得出tanZACO=tanZPCB,从而证出：ZACO=,PCB；(3)通过分类讨论，即可得出-l<n<l< n < |试题解析：(1)把点C (0, 3)代Ay = a(x - 1)(% - 3) (a > 0)得：3=3a•I a= 1即a的值为1(2) V a=l抛物线的解析式为：y = (% - 1)(% - 3) = %2 - 4x + 3 = (x — 2尸—1:.P (2, -1)•:B (3, 0) , C (0, 3):.CP=2 忑,BP^y/2, CB=3 近:.BP2 + BC2 = 20, CP? = (2A/5)2 = 20:.BP2 + BC2 = CP2.\ZCBP=90otanZPCB辔= ^ = | 连接AC•/tanZAOC=—=-OC 3tan ZPCB= tanZAOC・•・ ZAOC=ZPCB(3) ( i )当点0在BC左侧的抛物线上时由(2)可知Q (2, -1)m+n=2P为兀轴下方二次函数尸1 )(兀-3)(°>0)图像上一点l<m<3l<2-n<3 /.-l<n<l(ii)当点。

第二十二章第1节《二次函数的图象和性质》解答题专题 (10)1．已知关于x 的方程2(41)40kx k x -++=． （1）当k 取何值时，方程有两个实数根；（2）若二次函数2(41)4y kx k x =-++的图象与x 轴两个交点的横坐标均为整数，且k 为正整数，求k 值并用配方法求出抛物线的顶点坐标．2．抛物线2y x bx c =-++（b ，c 为常数）与x 轴交于点()1,0x 和()2,0x ，与y 轴交于点A ，点E 为抛物线顶点．（Ⅰ）当121,3x x =-=时，求点A ，点E 的坐标；（Ⅱ）若顶点E 在直线y x =上，当点A 位置最高时，求抛物线的解析式； （Ⅲ）若11,0x b =->，当(1,0)P 满足PA PE +值最小时，求b 的值．3．已知抛物线2y x bx c =++与x 轴交于()1,0A x ，()2,0B x 两点，且12xx <，若222133x x k +=（k 为正整数），我们把该抛物线称为“B 系抛物线”．特例感知（1）当2b =，15c =-时，请判断抛物线2y x bx c =++是否是“B 系抛物线”，并说明理由． 推广验证 （2）若234c b =-，且b 为负整数，请判断抛物线2y x bx c =++是否是“B 系抛物线”，并说明理由． 拓展应用（3）在（2）的条件下，若M 为该抛物线的顶点，且ABM ∆为等腰直角三角形，求该抛物线的解析式．4．已知：如图抛物线26y ax bx =++与x 轴交于点()6,0B ()2,0C -与y 轴交于点A ．（1）求抛物线的解析式；（2）如图点P 是线段AB 上方抛物线上的一个动点连结PA 、PB ．设PAB △的面积为S ．点P 的横坐标为m ．①试求S 关于m 的函数关系式；②请说明当点P 运动到什么位置时PAB △的面积有最大值？③过点P 作x 轴的垂线交线段AB 于点D 再过点P 做//PE x 轴交抛物线于点E 连结DE 请问是否存在点P 使PDE △为等腰直角三角形？若存在请直接写出点P 的坐标；若不存在请说明理由．5．在平面直角坐标系xOy 中抛物线()2420y axax a a =-+≠的顶点为P 且与y 轴交于点A 与直线y a =-交于点BC （点B 在点C 的左侧）.（1）求抛物线()2420y axax a a =-+≠的顶点P 的坐标（用含a 的代数式表示）；（2）横、纵坐标都是整数的点叫做整点记抛物线与线段AC 围成的封闭区域（不含边界）为“W 区域”.①当2a =时请直接写出“W 区域”内的整点个数；②当“W 区域”内恰有2个整点时结合函数图象直接写出a 的取值范围.6．在平面直角坐标系xOy 中，已知，点A （3，0）、B （－2，5）、C （0，－3）．求经过点A 、B 、C 的抛物线的表达式．7．在平面直角坐标系xOy 中，抛物线25y ax bx a =+-与y 轴交于点A ，将点A 向左平移4个单位长度，得到点B ，点B 在抛物线上． （1）求点B 的坐标（用含a 的式子表示）； （2）求抛物线的对称轴；（3）已知点()1,2P a --，()4,2Q -．若抛物线与线段PQ 恰有一个公共点，结合函数图象，求a 的取值范围．8．如图1在平面直角坐标系xOy 中抛物线y=-（x-a ）（x-4）（a ＜0）与x 轴交于A 、B 两点（点A 在点B 的左侧）与y 轴交于点C 点D 为抛物线的顶点．（1）若D 点坐标为（32524，）求抛物线的解析式和点C 的坐标；（2）若点M 为抛物线对称轴上一点且点M 的纵坐标为a 点N 为抛物线在x 轴上方一点若以C 、B 、M 、N 为顶点的四边形为平行四边形时求a 的值；（3）直线y=2x+b 与（1）中的抛物线交于点D 、E （如图2）将（1）中的抛物线沿着该直线方向进行平移平移后抛物线的顶点为D′与直线的另一个交点为E′与x 轴的交点为B′在平移的过程中求D′E′的长度；当∠E′D′B′=90°时求点B′的坐标．9．二次函数y=ax 2+bx+c （a≠0）的图象向左平移4个单位，再向上平移3个单位，得到二次函数y=x 2﹣2x+1，求：b ，c 的值． 10．在平面直角坐标系中，抛物线y 14=x 2沿x 轴正方向平移后经过点A （x 1，y 2），B （x 2，y 2），其中x 1，x 2是方程x 2﹣2x ＝0的两根，且x 1＞x 2， （1）如图．求A ，B 两点的坐标及平移后抛物线的解析式； （2）平移直线AB 交抛物线于M ，交x 轴于N ，且14AB MN =，求△MNO 的面积； （3）如图，点C 为抛物线对称轴上顶点下方的一点，过点C 作直线交抛物线于E 、F ，交x 轴于点D ，探究CD CDCE CF+的值是否为定值？如果是，求出其值；如果不是，请说明理由．11．已知：关于x 的二次函数2y x ax =-+（a ＞0），点A （n ，y 1）、B （n+1，y 2）、C （n+2，y 3）都在这个二次函数的图象上，其中n 为正整数．（1）y 1=y 2，请说明a 必为奇数；（2）设a=11，求使y 1≤y 2≤y 3成立的所有n 的值；（3）对于给定的正实数a ，是否存在n ，使△ABC 是以AC 为底边的等腰三角形？如果存在，求n 的值（用含a 的代数式表示）；如果不存在，请说明理由．12．如图①定义：直线:(0,0)l y mx n m n =+<>与x 、y 轴分别相交于A 、B 两点将AOB ∆绕着点O 逆时针旋转90°得到COD ∆过点A 、B 、D 的抛物线P 叫做直线l 的“纠缠抛物线”反之直线l 叫做P 的“纠缠直线"两线“互为纠缠线”．（1）若:22l y x =-+则纠缠物线P 的函数解析式是____________． （2）判断并说明22y x k =-+与212y x x k k=--+是否“互为纠缠线”． （3）如图②若纠缠直线:24l y x =-+纠缠抛物线P 的对称轴与CD 相交于点E 点F 在l 上点Q 在P 的对称轴上当以点C 、E 、Q 、F 为顶点的四边形是以CE 为一边的平行四边形时求点Q 的坐标．13．已知二次函数y ＝ax 2（a ≠0）的图象经过点（﹣2，3） （1）求a 的值，并写出这个二次函数的解析式； （2）求出此抛物线上纵坐标为3的点的坐标． 14．关于x 的二次函数y 1＝x 2+kx+k ﹣1（k 为常数） （1）对任意实数k ，函数图象与x 轴都有交点（2）若当x≥75时，函数y 的值都随x 的增大而增大，求满足条件的最小整数k 的值 （3）K 取不同的值时，函数抛物线的顶点位置也会变化，但会在某一函数图象上，求该函数图象的解析式（4）若当自变量x 满足0≤x≤3时，与其对应的函数值y 的最小值为10，求此时k 的值． 15．如图，在平面直角坐标系中，抛物线2y ax bx =+经过(2,4)A --，(2,0)B . （1）求抛物线2y ax bx =+的解析式.（2）若点M是该抛物线对称轴上的一点，求AM OM的最小值.16．在同一个直角坐标系中作出y＝12x2，y＝12x2－1的图象．(1)分别指出它们的开口方向、对称轴以及顶点坐标；(2)抛物线y＝12x2－1与抛物线y＝12x2有什么关系？17．如图：已知抛物线的顶点为A（1，4），抛物线与y轴交于点B（0，3）与x轴交于C、D两点，点P是x轴上的一个动点.（1）求抛物线的解析式；（2）当PA+PB的值是最小时，求点P的坐标.18．在平面直角坐标系中xOy中，抛物线y＝x2﹣4x+m+2的顶点在x轴上．（1）求抛物线的表达式；（2）点Q是x轴上一点，①若在抛物线上存在点P，使得∠POQ＝45°，求点P的坐标．②抛物线与直线y＝1交于点E，F（点E在点F的左侧），将此抛物线在点E，F（包含点E和点F）之间的部分沿x轴向左平移n个单位后得到的图象记为G，若在图象G上存在点P，使得∠POQ＝45°，求n的取值范围．19．如图，已知抛物线y=ax2+bx+3与x轴交于A、B两点，过点A的直线l与抛物线交于点C，其中A点的坐标是（1，0），C点坐标是（4，3）．（1）求抛物线的解析式；（2）在（1）中抛物线的对称轴上是否存在点D，使△BCD的周长最小？若存在，求出点D的坐标，若不存在，请说明理由；（3）若点E是（1）中抛物线上的一个动点，且位于直线AC的下方，试求△ACE的最大面积及E点的坐标．20．如图抛物线y=-x2+bx+c与x轴交于A、B两点交y轴正半轴于C点D为抛物线的顶点A （-10）B（30）．（1）求出二次函数的表达式．（2）点P在x轴上且∠PCB=∠CBD求点P的坐标．（3）在x轴上方抛物线上是否存在一点Q使得以QCBO为顶点的四边形被对角线分成面积相等的两部分？如果存在请直接写出点Q的坐标；如果不存在请说明理由．【答案与解析】1．（1）0k ≠；（2）k=1，（52，94-）.(1)要使方程有两个实数根，必须满足两个条件：[]2(41)440k k k ⎧∆=-+-⨯≥⎨≠⎩从而可求出k 的取值范围；(2)令y=0，得到一个一元二次方程，用含有k 的代数式表示方程的解，根据题意求出k 的值.(1)依题意得[]2(41)4400k k k ⎧∆=-+-⨯≥⎨≠⎩，整理得24k-100k ⎧∆=≥⎨≠⎩（）∵当k 取任何值时，2(41)0k -≥， ∴0k ≠∴当0k ≠时，方程总有两个实数根.(2)解方程2(41)40kx k x -++=，得14x =，21x k=． ∵12x x 和均为整数且k 为正整数，∴取k=1． ∴254y x x =-+222555()()422x x =-+-+ 259()24x =--∴抛物线的顶点坐标为（52，94-）．【点睛】本题考查二次函数综合题，解题的关键是掌握根的判别式和抛物线的顶点坐标的求法.2．（Ⅰ）()0,3A ，(1,4)E ；（Ⅱ）214y x x =-++；（Ⅲ）3b = （Ⅰ）将（-1，0），（3，0）代入抛物线的解析式求得b 、c 的值，确定解析式，从而求出抛物线与y 轴交于点A 的坐标，运用配方求出顶点E 的坐标即可；（Ⅱ）先运用配方求出顶点E 的坐标，再根据顶点E 在直线y x =上得出吧b 与c 的关系，利用二次函数的性质得出当b=1时，点A 位置最高，从而确定抛物线的解析式；（Ⅲ）根据抛物线经过（-1，0）得出c=b+1，再根据（Ⅱ）中顶点E 的坐标得出E 点关于x 轴的对称点E '的坐标，然后根据A 、P 两点坐标求出直线AP 的解析式，再根据点在直线AP 上，此时PA PE +值最小，从而求出b 的值.解：（Ⅰ）把点(-1,0)和(3,0)代入函数2y x bx c =-++，有10930b c b c --+=⎧⎨-++=⎩．解得2,3b c == 2223(1)4y x x x ∴=-++=--+(0,3),(1,4)A E ∴（Ⅱ）由222424b c b y x bx c x +⎛⎫=-++=--+ ⎪⎝⎭，得24,24b c b E ⎛⎫+ ⎪⎝⎭∵点E 在直线y x =上，2424b c b+∴=221111(1)4244c b b b ∴=-+=--+2110,(1)44A b ⎛⎫∴--+ ⎪⎝⎭ 当1b =时，点A 是最高点此时，214y x x =-++（Ⅲ）：抛物线经过点(1,0)-，有10b c --+=1c b ∴=+24,,(0,)24b c b E A c ⎛⎫+ ⎪⎝⎭ 2(2),,(0,1)24b b E A b ⎛⎫+∴+ ⎪⎝⎭∴E 关于x 轴的对称点E '为2(2),24b b ⎛⎫+- ⎪⎝⎭设过点A ，P 的直线为y kx t =+.把(0,1),(1,0)A b P +代入y kx t =+，得(1)(1)y b x =-+-把点2(2),24b b E '⎛⎫+- ⎪⎝⎭代入(1)(1)y b x =-+-.得2(2)(1)142b b b +⎛⎫=-+- ⎪⎝⎭，即2680b b --=解得，3b =0,3b b >∴=舍去.317b ∴=+ 【点睛】本题主要考查的是二次函数的综合应用，解答本题主要应用了待定系数法求二次的解析式、最短距离，数形结合思想及待定系数法的应用是解题的关键，属于中考压轴题．3．（1）是；理由见解析；（2）是；理由见解析；（3）23y 4x x =--． （1）根据“B 系抛物线”代入2b =，15c =-，然后计算与x 轴交点坐标，然后判断22213x x +的值判断即可；（2）将234c b =-代入表达式后计算与x 轴交点坐标，然后判断22213x x +的值判断即可； （3）过M 作MH ⊥AB ，然后根据（2）得到AB 长度和M 的横坐标，然后计算即可．解：（1）当2b =，15c =-时，代入2y x bx c =++即2215y x x =+-令y =0，即20215x x +=-∴(3)(x 5)0x -+= ∴125,3x x =-=∴22213x x +=2233?(-5)3k +=即28k=∴是“B 系抛物线” （2）∵234c b =-∴2234y x bx b =+-令y =0，即22304x bx b =+-∴13()()022x b x b -+= ∵b 为非负数 ∴1213,22x b x b ==- ∴2231()3?()322b b k -+=即233b k =此时2k b = ∴是“B 系抛物线”；（3）如图，当△ABM 为等腰直角三角形时，过M 作MH ⊥AB ，其中AB=2b ，点M 横坐标为2b - 将2b x =-代入2234y x bx b =+-即2223()()224b b y b b b =-+--= ∴MH=-2b∵△ABM 为等腰直角三角形 ∴MH=12AB ∴21×22b b -=解的120(),1b b ==-舍去∴抛物线的解析式234y x x =--【点睛】本题主要考查二次函数性质，理解“B 系抛物线”是解题的关键． 4．（1）2162y x bx =-++；（2）①()2327322S m =--+②当m=3时S 有最大值③点P 的坐标为（4,6）或（55-）．（1）由()2(6)(2)412y a x x a x x =-+=-- 则-12a=6求得a 即可； （2）①过点P 作x 轴的垂线交AB 于点D 先求出AB 的表达式y=-x+6设点21,262P m m m ⎛⎫-++ ⎪⎝⎭则点D （m-m+6）然后再表示()222113327332669322222S PD OB PD m m m m m m ⎛⎫=⨯⨯==-+++-=-+=--+ ⎪⎝⎭即可；②由在()2327322S m =--+中32-＜0故S 有最大值；③△PDE 为等腰直角三角形则PE=PD 然后再确定函数的对称轴、E 点的横坐标进一步可得|PE|=2m-4即21266242m m m m -+++-=-求得m 即可确定P 的坐标． 解：（1）由抛物线的表达式可化为()22(6)6=(2)412y a x x a x ax bx x =+-++-=- 则-12a=6解得：a=12-故抛物线的表达式为：2162y x bx =-++； （2）①过点P 作x 轴的垂线交AB 于点D由点A(0,6)、B 的坐标可得直线AB 的表达式为：y=-x+6 设点21,262P m m m ⎛⎫-++ ⎪⎝⎭则点D （m-m+6） ∴()222113327332669=322222S PD OB PD m m m m m m ⎛⎫=⨯⨯==-+++-=-+--+ ⎪⎝⎭； ②∵()2327322S m =--+32-＜0 ∴当m=3时S 有最大值； ③∵△PDE 为等腰直角三角形 ∴PE=PD ∵点21,262P m m m ⎛⎫-++ ⎪⎝⎭函数的对称轴为：x=2则点E 的横坐标为：4-m 则|PE|=2m-4 即21266242m m m m -+++-=- 解得：m=4或-2或517+517-2和517 当m=4时21262m m -++=6； 当m=517-21262m m -++=3175． 故点P 的坐标为（4,6）或（5173175）． 【点睛】本题属于二次函数综合应用题主要考查了一次函数、等腰三角形的性质、图形的面积计算等知识点掌握并灵活应用所学知识是解答本题的关键． 5．（1）顶点P 的坐标为()2,2a -；（2）① 6个；② 112a <≤112a -≤<-． （1）由抛物线解析式直接可求；（2）①由已知可知A （02）C （2+2 -2）画出函数图象观察图象可得；②分两种情况求：当a ＞0时抛物线定点经过（2-2）时a=1抛物线定点经过（2-1）时a=12则12＜a≤1；当a ＜0时抛物线定点经过（22）时a=-1抛物线定点经过（21）时a=-12则-1≤a<-12． 解：（1）∵y=ax 2-4ax+2a=a （x-2）2-2a ∴顶点为（2-2a ）；（2）如图①∵a=2∴y=2x 2-8x+2y=-2 ∴A （02）C （2-2） ∴有6个整数点；②当a ＞0时抛物线定点经过（2-2）时a=1 抛物线定点经过（2-1）时12a =； ∴112a <≤． 当0a <时抛物线顶点经过点（22）时1a =-； 抛物线顶点经过点（21）时12a =-； ∴ 112a -≤<-． ∴综上所述：112a <≤112a -≤<-． 【点睛】本题考查二次函数的图象及性质；熟练掌握二次函数的图象及性质是解题的关键．6．223y x x =--设抛物线的解析式为y=ax 2+bx+c ，再把三个已知点的坐标代入得到关于a 、b 、c 的方程组，解方程组即可得到二次函数的解析式．解：设经过点A 、B 、C 的抛物线的表达式为2(0)y ax bx c a =++≠．则9304253a b c a b c c ++=⎧⎪-+=⎨⎪=-⎩，解得：123a b c =⎧⎪=-⎨⎪=-⎩． ∴经过点A 、B 、C 的抛物线的表达式为223y x x =--． 【点睛】本题考查了用待定系数法求二次函数的解析式：在利用待定系数法求二函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解． 7．（1）()4,5B a --；（2）2x =-；（3）205a -≤< （1）根据解析式得到点A 的坐标，利用平移即可得到带你B 的坐标； （2）根据点A 、B 的对称性即可求出对称轴；（3）分两种情况：a>0或a<0时，分别确定点P 、Q 的位置，根据抛物线与线段PQ 恰有一个公共点求出答案.（1）∵抛物线25y ax bx a =+-与y 轴交于点A ，∴点A(0，-5a)，∵将点A 向左平移4个单位长度，得到点B ， ∴B(-4，-5a)； （2）对称轴是x=0422-=-； （3）如图：当a<0时，∵A(0，-5a), ()1,2P a --,且-5a>-2a ， ∴点P 在抛物线下方，∵()4,2Q -，抛物线与线段PQ 恰有一个公共点，B(-4，-5a)， ∴点Q 在抛物线上方或是在抛物线上，即25a ≥-， 解得25a ≥-， ∴205a -≤<时抛物线与线段PQ 恰有一个公共点；当a>0时，∵A(0，-5a), ()1,2P a --，且-5a<-2a<0， ∴点P 在抛物线上方，在x 轴下方， ∵()4,2Q -，B(-4，-5a)， ∴点Q 在抛物线上方，∴此时抛物线与线段PQ 没有公共点；综上，205a -≤<时抛物线与线段PQ 恰有一个公共点. 【点睛】此题考查抛物线的性质，利用解析式求点坐标，点平移的规律，抛物线对称轴，抛物线与线段交点问题.8．（1）y=-x 2+3x+4C （04）；（2）a 11326221-；（3）D ′E ′5B′（-10）．（1）将点D 的坐标代入函数解析式求得a 的值；利用抛物线解析式来求点C 的值． （2）需要分类讨论：BC 为边和BC 为对角线两种情况根据“平行四边形的对边平行且相等平行四边形的对角线相互平分”的性质列出方程组利用方程思想解答．（3）根据平移规律得到D ′E ′的长度、平移后抛物线的解析式然后由函数图象上点的坐标特征求得点B ′的坐标． （1）依题意得：254=-（32-a ）（32-4）． 解得a=-1．∴抛物线解析式为：y=-（x+1）（x-4）或y=-x 2+3x+4． ∴C （04）．（2）由题意知：A （a0）B （40）C （0-4a ）． 对称轴为直线x=42a +则M （42a +a ）． ①MN ∥BC 且MN=BC 根据点的平移特征可知N （42a --3a ）． 则-3a=-（42a --a ）（42a --4）． 解得：②当BC 为对角线时设N （xy ）．根据平行四边形的对角线互相平分可得：4424a x a y a +⎧+=⎪⎨⎪+=-⎩．解得425a x y a-⎧=⎪⎨⎪=-⎩．则-5a=-（42a --a ）（42a --4）． 解得a=63±．（舍去正值） ∴a 12=63-． （3）把D （32524，）代入y=2x+b 得到：2×32+b=254．则b=134． 故直线解析式为：y=2x+134． 联立2132434y x y x x ⎧=+⎪⎨⎪=-++⎩．解得1132254x y ⎧=⎪⎪⎨⎪=⎪⎩（舍去）221294x y ⎧=-⎪⎪⎨⎪=⎪⎩．∴E （-1294）∴．根据抛物线的平移规律则平移后线段D′E′始终等于 设平移后的D′（m2m+134）则E′（m-22m-34）． 平移后抛物线的解析式为：y=-（x-m ）2+2m+134． 则D′B′：y=-12x+n 过点（m2m+134） ∴y=-12x+52m+134则B′（5m+1320）． ∴-12（5m+132）+52m+134=0． 解得m 1=-32m 2=-138． ∴B ′1（-10）B′2（-1380）（与D′重合舍去）． 综上所述B′（-10）． 【点睛】本题主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养．要会利用数形结合的思想把代数和几何图形结合起来利用点的坐标的意义表示线段的长度从而求出线段之间的关系． 9．b=﹣10，c=22．此题实际上是将抛物线y=x 2﹣2x+1向下平移3个单位，向右平移4个单位得到抛物线y=ax 2+bx+c （a≠0），由此求得b ，c 的值．解：将y=x 2﹣2x+1向下平移3个单位，向右平移4个单位， 得：y=（x ﹣1﹣4）2﹣3=（x ﹣5）2﹣3=x 2﹣10x+22． 故：b=﹣10，c=22． 【点睛】本题考查了二次函数图象的平移，熟练掌握平移的规律：左加右减，上加下减，并用规律求函数解析式是关键．10．（1）点A 坐标为（2，0），点B 坐标为（0，1），21(2)4y x =-;（2）12或28；（3）CD CDCE CF+为定值，定值为1． （1）解方程x 2﹣2x ＝0得x 1＝2，x 2＝0．即可求得点A 坐标为（2，0），抛物线解析式为()2124y x =- ，把x ＝0代入抛物线解析式得y ＝1，即可得点B 坐标为（0，1）；（2）如图，过M 作MH ⊥x 轴，垂足为H ，由AB ∥MN ，即可得△ABO ∽△MHN ，根据相似三角形的性质可得14BO HN AB MH AO MN ===，由此求得MH ＝4，HN ＝8，将y ＝4代入抛物线()2124y x =-求得x 1＝﹣2，x 2＝6，所以M 1（﹣2，4），N 1（6，0），M 2（6，4），N 2（14，0）,由此求得△MNO 的面积即可；（3）设C （2，m ），求得CD 解析式为y ＝kx +m ﹣2k ，令y ＝0得kx +m ﹣2k ＝0，由此求得点D 为（2k mk-，0）；把CD 的解析式与抛物线的解析式联立221(2)4y kx m ky x =+-⎧⎪⎨=-⎪⎩，消去y 得，kx +m ﹣2k ＝14（x ﹣2）2．化简得x 2﹣4（k +1）x +4﹣4m +8k ＝0，由根与系数关系得，x 1+x 2＝4k +4，x 1•x 2＝4﹣4m +8k ．过E 、F 分别作EP ⊥CA 于P ，FQ ⊥CA 于Q ，由AD ∥EP ，AD ∥FQ ，可得CD CDCE CF+＝AD AD EP FQ AD EP FQ EP FQ ++=⋅⋅ ＝（2k mk -﹣2）×()()121212424x x x x x x +-⋅-++＝()()()4444482444k m k m k k +--⋅-+-++＝1，由此可得CD CD CE CF+为定值，定值为1． （1）解方程x 2﹣2x ＝0得x 1＝2，x 2＝0． ∴点A 坐标为（2，0），抛物线解析式为()2124y x =- ． 把x ＝0代入抛物线解析式得y ＝1． ∴点B 坐标为（0，1）．（2）如图，过M 作MH ⊥x 轴，垂足为H ∵AB ∥MN ∴△ABO ∽△MHN∴14BO HN AB MH AO MN === ∴MH ＝4，HN ＝8将y ＝4代入抛物线()2124y x =- 可得x 1＝﹣2，x 2＝6∴M 1（﹣2，4），N 1（6，0），M 2（6，4），N 2（14，0）, ∴11164122M N O S ∆=⨯⨯= 221144282M N O S ∆=⨯⨯=（3）设C （2，m ），设直线CD 为y ＝kx +b 将C （2，m ）代入上式，m ＝2k +b ，即b ＝m ﹣2k ． ∴CD 解析式为y ＝kx +m ﹣2k ， 令y ＝0得kx +m ﹣2k ＝0， ∴点D 为（2k mk-，0） 联立221(2)4y kx m k y x =+-⎧⎪⎨=-⎪⎩， 消去y 得，kx +m ﹣2k ＝14（x ﹣2）2． 化简得，x 2﹣4（k +1）x +4﹣4m +8k ＝0由根与系数关系得，x 1+x 2＝4k +4，x 1•x 2＝4﹣4m +8k ．过E 、F 分别作EP ⊥CA 于P ，FQ ⊥CA 于Q ， ∴AD ∥EP ，AD ∥FQ ， ∴CD CD CE CF+＝AD ADEP FQ AD EP FQ EP FQ ++=⋅⋅ ＝（2k mk-﹣2）×()()121212424x x x x x x +-⋅-++＝()()()4444482444k mk m k k +--⋅-+-++ ＝1∴CD CDCE CF +为定值，定值为1． 【点睛】本题是二次函数综合题，考查了一次函数与二次函数图象的交点问题，解决第（3）问的关键是确定CD CD CE CF+＝AD ADEP FQ AD EP FQ EP FQ ++=⋅⋅，再利用根与系数的关系解决． 11．解：（1）∵点A （n ，y 1）、B （n+1，y 2）都在二次函数2y x ax =-+（a ＞0）的图象上，∴()()2212y n an y n 1a n 1=-+=-+++，． ∵y 1=y 2，∴()()22n an n 1a n 1-+=-+++，整理得：a=2n+1． ∵n 为正整数，∴a 必为奇数． （2）当a=11时，∵y 1＜y 2＜y 3，∴()()()()222n 11n n 111n 1n 211n 2-+≤-+++≤-+++． 化简得：0102n 184n ≤-≤-．解得：n 4≤． ∵n 为正整数，∴n=1、2、3、4． （3）存在． 假设存在，则AB=AC ，如图所示，过点B 作BN ⊥x 轴于点N ，过点A 作AD ⊥BN 于点D ，CE ⊥BN 于点E ，∵x A =n ，x B =n+1，x C =n+2，∴AD=CE=1． 在Rt △ABD 与Rt △CBE 中，AB=BC ，AD=CE ， ∴Rt △ABD ≌Rt △CBE （HL ）．∴∠BAD=∠CBE ，即BN 为顶角的平分线． 由等腰三角形性质可知，点A 、C 关于BN 对称． ∴BN 为抛物线的对称轴，点B 为抛物线的顶点， ∴()a an 1212+=-=⨯-．∴a n 12=-．∴存在n ，使△ABC 是以AC 为底边的等腰三角形，an 12=-． （1）将点A 和点B 的坐标代入二次函数的解析式，利用y 1=y 2得到用n 表示a 的式子，即可得到答案；（2）将a=11代入解析式后，由题意列出不等式组，求得此不等式组的正整数解． （3）本问为存在型问题，如图所示，可以由三角形全等及等腰三角形的性质，判定点B为抛物线的顶点，点A 、C 关于对称轴对称，于是得到()a a n 1212+=-=⨯-，从而可以求出a n 12=-． 12．答案见解析.（1）若l ：y=-2x+2则点A 、B 、C 、D 的坐标分别为：（10）、（02）、（01）、（-20）则抛物线的表达式为：y=a （x+2）（x-1）即可求解；（2）同理：点A 、B 、C 、D 的坐标分别为：（k0）、（02k ）、（0k ）、（-2k0）则抛物线的表达式为：y=a （x+2k ）（x-k ）即可求解；（3）以点C 、E 、Q 、F 为顶点的四边形是以CE 为一边的平行四边形时由题意得：|x Q -x F |=1即：m+1=±1即可求解．解：（1）若l ：y=-2x+2则点A 、B 、C 、D 的坐标分别为：（10）、（02）、（01）、（-20）则抛物线的表达式为：y=a （x+2）（x-1）将点B 的坐标代入上式得：2=a （0+2）（0-1）解得：a=-1故答案为：y=-x 2-x+2；(2)同理：点A 、B 、C 、D 的坐标分别为：（k0）、（02k ）、（0k ）、（-2k0） 则抛物线的表达式为：y=a （x+2k ）（x-k ）将点B 的坐标代入上式并解得：a=1-k 故抛物线的表达式为：y=211-(2)()2x k x k x x k k k +-=--+ 故y=-2x+2k 与y ＝212x x k k--+“互为纠缠线”； 点A 、B 、C 、D 的坐标分别为：（20）、（04）、（02）、（-40） 同理可得：抛物线的表达式为：y=21--42x x + 抛物线的对称轴为：x=-1设点F （m-2m+4）点Q （-1n ）将点C 、D 的坐标代入一次函数表达式并求得：直线CD 的表达式为：y=12x+2 点CE 横坐标差为1故纵坐标差为12以点C 、E 、Q 、F 为顶点的四边形是以CE 为一边的平行四边形时由题意得：|x Q -x F |=1即：m+1=±1解得：m=0或-2当m=0时点F （04）则点Q （-192）；同理当m=-2时点Q （-1172）； 综上点Q 坐标为：Q （-192）或Q （-1172）． 【点睛】 本题考查的是二次函数综合运用涉及到一次函数、平行四边形性质等其中（3）要注意分类求解避免遗漏．13．（1）34，234y x = （2）（﹣2，3），（2，3） （1）根据二次函数图象上点的坐标满足其解析式，把点（-2，3）代入解析式得到关于a 的方程，然后解方程即可；（2）把y=3代入解析式求出x 的值即可．解：（1）∵抛物线y ＝ax 2经过点（﹣2，3），∴4a ＝3，∴a=34， ∴二次函数的解析式为234y x =； （2）∵抛物线上点的纵坐标为3， ∴3＝34x 2， 解得x ＝±2， ∴此抛物线上纵坐标为3的点的坐标为（﹣2，3），（2，3）．【点睛】考查了待定系数法求解析式，二次函数图象上点的坐标特征，函数解析式与图象上的点之间的关系，点在图象上，则满足解析式；反之，满足解析式则在函数图象上．14．（1）见解析；（2）﹣150；（3）y ＝﹣x 2﹣2x ﹣1；（4）11．（1）计算△，根据△的值进行判断；（2）根据二次函数的增减性即可判断；（3）得到抛物线的顶点，写成方程组，消去k 得y =-x 2-2x -1，即可判断；（4）函数配方后得y =x 2+kx +k -1=22124k k x k ⎛⎫+-+- ⎪⎝⎭，根据对称轴的位置分三种情况进行讨论可得结论.解：（1）∵△＝k 2﹣4（k ﹣1）＝k 2﹣4k+4＝（k ﹣2）2≥0，∴对任意实数k ，函数图象与x 轴都有交点；（2）∵a＝1＞0，抛物线的对称轴x b k 2a 2=-=-， ∴在对称轴的右侧函数y 的值都随x 的增大而增大，即当x k 2-＞时，函数y 的值都随x 的增大而增大， ∵x≥75时，函数y 的值都随x 的增大而增大， ∴k 2-≤75，k≥﹣150， ∴k 的最小整数是﹣150， ∴满足条件的最小整数k 的值是﹣150；（3）∵y＝x 2+kx+k ﹣1＝（x k 2+）22k 4-+k ﹣1， ∴抛物线的顶点为（k 2-，2k 4-+k ﹣1）， ∴2k x 2k y k 14⎧=-⎪⎪⎨⎪=-+-⎪⎩， 消去k 得，y ＝﹣x 2﹣2x ﹣1，由此可见，不论k 取任何实数，抛物线的顶点都满足函数y ＝﹣x 2﹣2x ﹣1，即抛物线的顶点在二次函数y ＝﹣x 2﹣2x ﹣1的图象上； （4）∵y＝x 2+kx+k ﹣1＝（x k 2+）22k 4-+k ﹣1， ∴抛物线的顶点为（k 2-，2k 4-+k ﹣1）， 又∵0≤x≤3时，与其对应的函数值y 的最小值为10， ①当k 2-≤0时，即k≤0， 此时x ＝0时，y 取得最小值是10，则有10＝k ﹣1，k ＝11． ②当k 2-≥3时，即k≤﹣6， 此时x ＝3时，y 取得最小值是10，则有10＝32+3k+k ﹣1， k 12=，不符合题意； ③当0k 2-＜＜3时，即﹣6＜k ＜0， 此时x k 2=-时，y 取得最小值是10，即2k 4-+k ﹣1＝10， 此方程无实根，综上所述，k 的值是11．【点睛】本题主要考查了二次函数的性质，解决本题的关键是要熟悉函数关系式和方程的关系、函数的性质.15．（1）抛物线的解析式为212y x x =-+；（2）AM OM +的最小值为42. （1）利用待定系数法可求出该抛物线的解析式； （2）根据O 、B 两点正好关于抛物线的对称轴对称，那么只需连接A 、B ，直线AB 和抛物线对称轴的交点即为符合要求的M 点，而AM +OM 的最小值正好是AB 的长，过点A 作AN ⊥x 轴于点N ．在Rt △ABN 中，根据勾股定理即可得出结论．（1）把A （﹣2，﹣4），B （2，0）两点的坐标代入y =ax 2+bx 中，得：424420a b a b -=-⎧⎨+=⎩，解方程组，得：a 12=-，b =1，∴解析式为y 12=-x 2+x ． （2）由y 12=-x 2+x 12=-（x ﹣1）212+，可得抛物线的对称轴为直线x =1，并且对称轴垂直平分线段OB ，∴OM =BM ，∴OM +AM =BM +AM ．连接AB 交直线x =1于M 点，则此时OM +AM 最小．过点A 作AN ⊥x 轴于点N ．在Rt △ABN 中，AB 222244AN BN =+=+=42，因此OM +AM 最小值为42．【点睛】本题是二次函数的综合题，难点在于点M 位置的确定，正确理解二次函数的轴对称性以及两点之间线段最短是解题的关键．16．见解析试题分析：观察图像结合函数表达式可以得到两个函数开口向上，对称轴也都是y 轴，顶点坐标分别是(0,0),（0，-1）；根据二次函数的性质及图像知道抛物线y＝12x2－1与抛物线y＝12x2形状相同，对称轴相同，但是位置不同，开口方向也相同，所以可以得到抛物线y＝12x2－1可由抛物线y＝12x2向下平移1个单位长度得到的．解：如图所示：(1)抛物线y＝12x2开口向上，对称轴为y轴，顶点坐标(0，0)；抛物线y＝12x2－1开口向上，对称轴为y轴，顶点坐标(0，－1)．(2)抛物线y＝12x2－1可由抛物线y＝12x2向下平移1个单位长度得到．17．（1）y=﹣（x﹣1）2+4；（2）当PA+PB的值是最小时，点P的坐标是（37，0）.试题分析：（1）由题意可设抛物线解析式为“顶点式”，再代入点B的坐标可求得解析式；（2）由题意作出点B关于x轴的对称轴点E，连接AE交x轴于点P，P为所求的点，由A、E的坐标可求得直线AE的解析式，再由AE的解析式就可求得点P的坐标.试题解析：(1)∵抛物线的顶点A的坐标为（1，4），∴设抛物线的表达式为y＝a(x－1)2＋4.∵抛物线过点B(0，3)，∴3＝a(0－1)2＋4.解得a＝－1.∴二次函数的表达式为y＝－(x－1)2＋4，即y＝－x2＋2x＋3.(2)作点B关于x轴的对称点E(0，－3)，连接AE交x轴于点P，点P即为所求点．设AE所在直线的表达式为y＝kx＋b，分别代入A，E坐标，得43k bb+=⎧⎨=-⎩，解得73kb=⎧⎨=-⎩，∴y＝7x－3.当y＝0时，x＝3 7 .∴点P 的坐标为(37，0)． 18．（1）y ＝x 2﹣4x +4；（2）①点P 的坐标为（1，1）或（4，4）；②在图象G 上存在点P ，使得∠POQ ＝45°，n 的取值范围为0≤n ≤4．（1）根据抛物线顶点在x 轴上，列式计算可得m 的值；（2）由∠POQ ＝45°，作直线y ＝x ，交抛物线y ＝x 2﹣4x +4于点P ，联立解析式求出P 点坐标即可；（3）分两种情况考虑：当点P ，Q 在y 轴右侧时与点P ，Q 在y 轴左侧时，列出不等式求解即可.解：（1）∵抛物线y ＝x 2﹣4x +m +2的顶点在x 轴上，∴()()2412441m ⨯⨯+--⨯＝0，解得：m ＝2， ∴抛物线的表达式为y ＝x 2﹣4x +4．（2）①作直线y ＝x ，交抛物线y ＝x 2﹣4x +4于点P ，如图1所示．联立直线OP 及抛物线的表达式成方程组，得：244y x y x x =⎧⎨=+⎩﹣， 解得：1111x y =⎧⎨=⎩，2244x y =⎧⎨=⎩， ∴点P 的坐标为（1，1）或（4，4）．②当y ＝1时，x 2﹣4x +4＝1，解得：x 1＝1，x 2＝3，∴点E 的坐标为（1，1），点F 的坐标为（3，1）．分两种情况考虑：（i ）当点P ，Q 在y 轴右侧时，∵抛物线y ＝x 2﹣4x +4与直线y ＝x 交于点（1，1）， ∴当1≤3﹣n ≤3时，图象G 上存在点P ，使得∠POQ ＝45°，解得：0≤n ≤2；（ii ）当点P ，Q 在y 轴左侧时，同①可得出，抛物线y ＝x 2﹣4x +4与直线y ＝﹣x 交于点（﹣1，﹣1）或（﹣4，﹣4），∴当﹣1≤3﹣n ≤1时，图象G 上存在点P ，使得∠POQ ＝45°，解得：2≤n ≤4． 综上所述：若在图象G 上存在点P ，使得∠POQ ＝45°，n 的取值范围为0≤n ≤4．【点睛】本题考查二次函数的图像和性质，正确理解∠POQ＝45°的意义，运用数形结合的思想解决问题是解题关键.19．（1）y=x2﹣4x+3；（2）存在，抛物线对称轴上存在点D（2，1），使△BCD的周长最小；（3）△ACE的最大面积278，此时E点坐标为（52，34）．（1）利用待定系数法求二次函数解析式解答即可．（2）利用待定系数法求出直线AC的解析式，然后根据轴对称确定最短路线问题，直线AC 与对称轴的交点即为所求点D．（3）根据直线AC的解析式，设出过点E与AC平行的直线，然后与抛物线解析式联立消掉y得到关于x的一元二次方程，利用根的判别式△=0时，△ACE的面积最大，然后求出此时与AC平行的直线，然后求出点E的坐标，并求出该直线与x轴的交点F的坐标，再求出AF ，再根据直线l 与x 轴的夹角为45°求出两直线间的距离，再求出AC 间的距离，然后利用三角形的面积公式列式计算即可得解．解：（1）∵抛物线y=ax 2+bx+3经过点A （1，0），点C （4，3），∴a b 30{16a 4b 33++=++=，解得a 1{b 4==-． ∴抛物线的解析式为y=x 2﹣4x+3．（2）存在．∵点A 、B 关于对称轴对称，∴点D 为AC 与对称轴的交点时△BCD 的周长最小． ∵y=x 2﹣4x+3=（x ﹣2）2﹣1，∴抛物线的对称轴为直线x=2．设直线AC 的解析式为y=kx+b （k≠0），则k b 0{4k b 3+=+=，解得：k 1{b 1==-．∴直线AC 的解析式为y=x ﹣1．当x=2时，y=2﹣1=1．∴抛物线对称轴上存在点D （2，1），使△BCD 的周长最小．（3）如图，设过点E 与直线AC 平行线的直线为y=x+m ，联立243y x my x x =+⎧⎨=-+⎩，消掉y 得，x 2﹣5x+3﹣m=0．由△=（﹣5）2﹣4×1×（3﹣m ）=0得m=134-．∴m=134-时，点E 到AC 的距离最大，△ACE 的面积最大．此时x=52，y=5133244-=-．∴点E 的坐标为（52，34-）．设过点E 的直线与x 轴交点为F ，则F （134，0）．∴AF=139144-=．∵直线AC 的解析式为y=x ﹣1，∴∠CAB=45°．∴点F 到AC 的距离为9292428⨯=． 又∵223(41)32AC =+-=．∴△ACE 的最大面积192273228=⨯⨯=，此时E 点坐标为（52，34-）． 20．（1）y=-x 2+2x+3；（2）P （60）或P 3,02⎛⎫ ⎪⎝⎭；（3）存在点Q 113113,⎛⎫++ ⎪ ⎪⎝⎭或17,24⎛⎫- ⎪⎝⎭． （1）将点A 、B 坐标代入解析式求出b 、c 的值即可得；（2）∠PCB=∠CBD 有两种情况①P 在B 的右侧时延长BD 交y 轴于点H 由∠OCB=∠OBC=45°可证明∠HCB=∠CBP 从而△PCB ≌△HBC 由直线BD 即可求得：OH=OP=6从而得到P 点坐标；②P 在B 的左侧时此时PC ∥BD 根据一次函数解析式即可求出P ； （3）分以下两种情况分别求解①点Q 在y 轴右侧时由OB=OC 可得出OQ 是∠BOC 的平分线联立二次函数解析式与直线OQ 的解析式即可求解；②点Q 在y 轴左侧时可得这条对角线只能是BQ 过点C 作x 轴的平行线EF 过点QB 分别作EF 的垂线垂足分别为FE 延长FQ 交x 轴于点G 设点Q 的坐标为(mn)根据S △BOQ =S △CBQ =S 梯形FQBE -S △FCQ -S △BEC 可得出关于mn 的关系式再与二次函数的解析式联立即可求解．解：（1）将点A （-10）B （30）代入y=-x 2+bx+c 得10930b c b c --+=⎧⎨-++=⎩解得23b c =⎧⎨=⎩∴二次函数的表达式为y=-x 2+2x+3；（2）①当点P 在点B 右侧时延长BD 交y 轴于点H∵y=-x 2+2x+3=-（x-1）2+4∴点D 的坐标为（14）设直线BD 的解析式为y=kx+b 则304k b k b +=⎧⎨+=⎩解得26k b =-⎧⎨=⎩即直线BD 的解析式为y=-2x+6 ∴点H 的坐标为（06）∵OB=OC=3∴∠OBC=∠OCB=45°∴∠HCB=∠CBP=135°又∠PCB=∠CBDBC=BC∴△PCB ≌△HBC∴CH=PB∴OH=OB=6故此时点P 的坐标为（60）；②当点P （P′）在点B 左侧时直线BD 的表达式为：y=-2x+6∵∠P′CB=∠CBD 则P′C ∥BD则直线P′C 的表达式为：y=-2x+3当y=0x=32故此时点P′的坐标为3,02⎛⎫ ⎪⎝⎭综上所述点P 的坐标为（60）或3,02⎛⎫⎪⎝⎭； （3）存在．理由如下：①当点Q 在y 轴右侧时以QCBO 为顶点的四边形被对角线分成面积相等的两部分这条对角线只能是OQS △COQ =S △BOQ 如图而OB=OC 故OQ 是∠BOC 的平分线即OQ 的函数表达式为：y=x将y=x 与y=-x 2+2x+3联立得-x 2+2x+3=x 解得113+ 故此时点Q 的坐标为（1132+1132+）； ②当点Q 在y 轴左侧时以QCBO 为顶点的四边形被对角线分成面积相等的两部分这条对角线只能是BQS △BOQ =S △CBQ 如图过点C 作x 轴的平行线EF 过点QB 分别作EF 的垂线垂足分别。

中考专题训练——二次函数与特殊的四边形1．已知二次函数y＝a（x﹣1）2+k的图象与x轴交于A，B两点，AB＝4，与y轴交于C点，E为抛物线的顶点，∠ECO＝135°．（1）求二次函数的解析式；（2）若P在第四象限的抛物线上，连接AE交y轴于点M，连接PE交x轴于点N，连接MN，且S△EAP＝3S△EMN，求点P的坐标；（3）过直线BC上两点P，Q（P在Q的左边）作y轴的平行线，分别交抛物线于N，M，若四边形PQMN 为菱形，求直线MN的解析式．2．如图，在平面直角坐标系中，抛物线y＝ax2+bx+c（a＞0）与x轴交于点A（﹣2，0）和点B，与y轴交于点C，对称轴为直线x＝12．（1）请用a的代数式表示C点坐标．（2）连接AC，BC，若△ABC的面积为10，求该抛物线的解析式．（3）在（2）的条件下，点P是直线y＝x+2上一点（位于x轴下方），点Q是反比例函数y＝kx（k＞0）图象上一点，若以点A，C，P，Q为顶点的四边形是菱形，则直接写出k的值（不需要写出计算过程）．3．如图，在平面直角坐标系中，抛物线y＝x2+bx+c交x轴于A，B两点，交y轴于点C，直线y＝x﹣3经过B，C两点．（1）求抛物线的解析式；（2）点P是第四象限内抛物线上的动点，过点P作PD⊥x轴于点D，交直线BC于点M，连接AC，过点M作MN⊥AC于点N，设点P的横坐标为t．①求线段MN的长d与t之间的函数关系式（不要求写出自变量t的取值范围）；②点Q是平面内一点，是否存在一点P，使以B，C，P，Q为顶点的四边形为矩形？若存在，请直接写出t 的值；若不存在，请说明理由．4．如图，抛物线y＝ax2+bx+2经过A（﹣1，0），B（2，0）两点，与y轴交于点C．（1）求抛物线的解析式；（2）M在抛物线上，线段MA绕点M顺时针旋转90°得MD，当点D在抛物线的对称轴上时，求点M的坐标；（3）P在对称轴上，Q在抛物线上，以P，Q，B，C为顶点的四边形为平行四边形，直接写出点P的坐标．5．如图，在平面直角坐标系内，抛物线223=-++与x轴交于点A，C（点A在点C的左侧），与y轴y x x交于点B，顶点为D．点Q为线段BC的三等分点（靠近点C）.△的周长最（1）点M为抛物线对称轴上一点，点E为对称轴右侧抛物线上的点且位于第一象限，当MQC △面积的最大值；小时，求CME（2）在（1）的条件下，当CME △的面积最大时，过点E 作EN x ⊥轴，垂足为N ，将线段CN 绕点C 顺时针旋转90°得到点N ，再将点N 向上平移16个单位长度.得到点P ，点G 在抛物线的对称轴上，请问在平面直角坐标系内是否存在一点H ，使点D ，P ，G ，H 构成菱形.若存在，请直接写出点H 的坐标，若不存在，请说明理由.6．如图，在平面直角坐标系中，抛物线y =-x 2+bx +c 经过点（0，6），其对称轴为直线x =32．在x 轴上方作平行于x 轴的直线l 与抛物线交于A 、B 两点（点A 在对称轴的右侧），过点A 、B 作x 轴的垂线，垂足分别为D 、C ．设A 点的横坐标为m ．（1）求此抛物线所对应的函数关系式．（2）当m 为何值时，矩形ABCD 为正方形．（3）当m 为何值时，矩形ABCD 的周长最大，并求出这个最大值．7．如图1，在平面直角坐标系中，抛物线249y x bx c =-++经过点()5,0A -和点()10B ,．(1)求抛物线的解析式及顶点D 的坐标；(2)点P 是抛物线上A 、D 之间的一点，过点P 作PE x ⊥轴于点E ，PG y ⊥轴，交抛物线于点G ，过点G 作GF x ⊥轴于点F ，当矩形PEFG 的周长最大时，求点P 的横坐标；(3)如图2，连接AD 、BD ，点M 在线段AB 上(不与A 、B 重合)，作DMN DBA ∠=∠，MN 交线段AD 于点N ，是否存在这样点M ，使得DMN ∆为等腰三角形？若存在，求出AN 的长；若不存在，请说明理由．8．如图，在平面直角坐标系xOy 中，二次函数y ＝x 2﹣2x +m （m ＞0）的对称轴与比例系数为5的反比例函数图象交于点A ，与x 轴交于点B ，抛物线的图象与y 轴交于点C ，且OC ＝3OB ．（1）求点A 的坐标；（2）求直线AC 的表达式；（3）点E 是直线AC 上一动点，点F 在x 轴上方的平面内，且使以A 、B 、E 、F 为顶点的四边形是菱形，直接写出点F 的坐标．9．如图1（注：与图2完全相同），在直角坐标系中，抛物线经过点三点0(1)A ，,(50)B ，,4(0)C ，．（1）求抛物线的解析式和对称轴；（2）P 是抛物线对称轴上的一点，求满足PA PC +的值为最小的点P 坐标（请在图1中探索）； （3）在第四象限的抛物线上是否存在点E ，使四边形OEBF 是以OB 为对角线且面积为12的平行四边形？若存在，请求出点E 坐标，若不存在请说明理由.（请在图2中探索）10．在平面直角坐标系中,抛物线C 1:y=x²+bx+c 的图象与x 轴交于A 、B 两点,A 点在原点的左侧,B 点的坐标为(3.0)，与y 轴交于C （0，-3）（1）求抛物线C 1的表达式；（2）分别写出抛物线C 1关于B 点，关于A 点的对称抛物线C 2， C 3的函数表达式（3）设C 1的顶点为D ，C 2与x 轴的另一个交点为A 1顶点为D 1，C 3与x 轴的另一个交点为B 1，顶点为D 2，在以A 、B 、D 、A 1、B 1、D 1、D 2这七个点中的四个点为顶点的四边形中，求面积最大的四边形的面积．11．综合与探究如图，抛物线26y ax bx =++经过点A(-2,0)，B(4,0)两点，与y 轴交于点C ，点D 是抛物线上一个动点，设点D 的横坐标为(14)m m <<.连接AC ，BC ，DB ，DC ，(1)求抛物线的函数表达式；(2)△BCD 的面积等于△AOC 的面积的34时，求m 的值； (3)在(2)的条件下，若点M 是x 轴上的一个动点，点N 是抛物线上一动点，试判断是否存在这样的点M,使得以点B ，D ，M ，N 为顶点的四边形是平行四边形，若存在，请直接写出点M 的坐标；若不存在，请说明理由.12．如图，在平面直角坐标系中，Rt ABC ∆的边BC 在x 轴上，90ABC ∠=，以A 为顶点的抛物线2y x bx c =-++经过点(3,0)C ，交y 轴于点(0,3)E ，动点P 在对称轴上．（1）求抛物线解析式；（2）若点P 从A 点出发，沿A B →方向以1个单位/秒的速度匀速运动到点B 停止，设运动时间为t 秒，过点P 作PD AB ⊥交AC 于点D ，过点D 平行于y 轴的直线l 交抛物线于点Q ，连接,AQ CQ ，当t 为何值时，ACQ ∆的面积最大？最大值是多少？（3）若点M 是平面内的任意一点，在x 轴上方是否存在点P ，使得以点,,,P M E C 为顶点的四边形是菱形，若存在，请直接写出符合条件的M 点坐标；若不存在，请说明理由．13．如图，已知抛物线2y ax bx c =++的顶点为()4,3A ，与y 轴相交于点()0,5B -，对称轴为直线l ，点M 是线段AB 的中点.（1）求抛物线的表达式；（2）写出点M 的坐标并求直线AB 的表达式；（3）设动点P ，Q 分别在抛物线和对称轴l 上，当以A ，P ，Q ，M 为顶点的四边形是平行四边形时，求P ，Q 两点的坐标.14．如图①，抛物线2y ax bx a b =+--与x 轴相交于()5,0A -、B 两点，过点A 的直线y x t =+与y 轴和抛物线相交于点C .（1）求抛物线的解析式和点C 的坐标；（2）点P 是抛物线上的一动点，当点P 在直线AC 的上方时，连接OP 、PC ，并把POC ∆沿着OC 翻折得到'P OC ∆，是否存在点P ，使得到四边形'POP C 为菱形，若存在，请求出点P 的坐标；若不存在，请说明理由.（3）如图②，动点E 在线段OA 上，过点E 作x 轴的垂线与AC 交于点M ，与拋物线交于点N ，试问：抛物线上是否存在点Q ，使EQN ∆与BEM ∆的面积相等时，线段NQ 的长度有最小值？若存在，请求出点Q 的坐标；若不存在，请说明理由.15．如图，已知抛物线1M ：22y ax x =-与直线y x =的一个交点记为A ，点A 的横坐标是3.将抛物线1M ：22y ax x =-向左平移3个单位，再向下平移3个单位，得到抛物线2M ，直线y x =与2M 的一个交点记为B ，点C 是线段AB 上的一个动点，过点C 作x 轴的垂线，垂足为D ，在CD 的右侧作正方形CDEF .（1）求抛物线1M 的表达式及顶点坐标；（2）当点C 的横坐标为2时，直线y x n =+恰好经过正方形CDEF 的顶点F ，求此时n 的值； （3）在点C 的运动过程中，若直线y x n =+与正方形CDEF 始终没有公共点，求n 的取值范围. 16．如图①，在平面直角坐标系xOy 中，抛物线2y x bx c =++与x 轴交于点A 、C ，与y 轴交于点B ，抛物线的顶点在直线4y x =-上，且横坐标为0，已知2OA =.（1）求抛物线的解析式；（2）如图②，将抛物线沿直线4y x =-平移得到新抛物线，设新抛物线顶点的横坐标为m ，在平移过程中，若新抛物线与直线AB 有且只有一个公共点，求m 的值；（3）设新抛物线的顶点为P ，在平移的过程中，在y 轴上是否存在一点Q ，使得以点A ，B ，P ，Q 为顶点的四边形为平行四边形，若存在，请求出Q 点的坐标；若不存在，请说明理由.17．如图，已知二次函数()31:430L y ax ax a a =-+>与x 轴交于A ，B 两点，与y 轴交于点C ，过点C 作直线//CD x 轴交抛物线1L 于一点D ，将抛物线1L 沿着直线CD 翻折，并向右平移m 个单位()0m ≥，得到抛物线2L ，抛物线2L 交直线CD 于E ，F 两点（E 在F 的左边），点M ，N 分别是1L ，2L 的顶点，连接CN ，NF ，FM ，MC 得到四边形CNFM.（1）当1a =，0m =时，直接写出抛物线2L 的解析式；（2）若点D ，E 是线段CF 三等分点，求m 的值；（3）在平移过程中，是否存在以点C ，N ，F ，M 为顶点的四边形是矩形的情形，若存在，求出m 应满足的关系式，若不存在，请说明理由.18．如图1，在平面直角坐标系中，抛物线y ＝﹣12x 2﹣72x ﹣3交x 轴于A ，B 两点（点A 在点B 的左侧），交y 轴于点C（1）求直线AC 的解析式；（2）点P 是直线AC 上方抛物线上的一动点（不与点A ，点C 重合），过点P 作PD ⊥x 轴交AC 于点D ，求PD 的最大值；（3）将△BOC 沿直线BC 平移，点B 平移后的对应点为点B ′，点O 平移后的对应点为点O ′，点C 平移后的对应点为点C ′，点S 是坐标平面内一点，若以A ，C ，O ′，S 为顶点的四边形是菱形，求出所有符合条件的点S 的坐标．19．已知抛物线23y ax bx =+-经过点(1,1)A -，(3,3)B -．把抛物线23y ax bx =+-与线段AB 围成的封闭图形记作G ．（1）求此抛物线的解析式；（2）点P 为图形G 中的抛物线上一点，且点P 的横坐标为m ，过点P 作//PQ y 轴，交线段AB 于点Q ．当APQ △为等腰直角三角形时，求m 的值；（3）点C是直线AB上一点，且点C的横坐标为n，以线段AC为边作正方形ACDE，且使正方形ACDE与图形G在直线AB的同侧，当D，E两点中只有一个点在图形G的内部时，请直接写出n的取值范围．20．如图，已知二次函数L1：y＝mx2+2mx﹣3m+1（m≥1）和二次函数L2：y＝﹣m（x﹣3）2+4m﹣1（m≥1）图象的顶点分别为M，N，与x轴分别相交于A、B两点（点A在点B的左边）和C、D两点（点C在点D的左边）．（1）函数y＝mx2+2mx﹣3m+1（m≥1）的顶点坐标为______；当二次函数L1，L2的y值同时随着x的增大而增大时，则x的取值范围是______；（2）当AD＝MN时，判断四边形AMDN的形状（直接写出，不必证明）；（3）抛物线L1，L2均会分别经过某些定点，①求所有定点的坐标；②若抛物线L1位置固定不变，通过左右平移抛物线L2的位置使这些定点组成的图形为菱形，则抛物线L2应平移的距离是多少？。

2023年九年级数学中考复习：二次函数综合压轴题（特殊三角形问题）1．如图，直线y=﹣23x+c与x轴交于点A（3，0），与y轴交于点B，抛物线y=﹣43x2+bx+c经过点A，B，M（m，0）为x轴上一动点，点M在线段OA上运动且不与O，A重合，过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P，N．（1）求点B的坐标和抛物线的解析式；（2）在运动过程中，若点P为线段MN的中点，求m的值；（3）在运动过程中，若以B，P，N为顶点的三角形与△APM相似，求点M的坐标；2．如图△，已知抛物线y＝ax2﹣4amx+3am2（a、m为参数，且a＞0，m＞0）与x轴交于A、B两点（A在B的左边），与y轴交于点C．（1）求点B的坐标（结果可以含参数m）；（2）连接CA、CB，若C（0，3m），求tan△ACB的值；（3）如图△，在（2）的条件下，抛物线的对称轴为直线l：x＝2，点P是抛物线上的一个动点，F是抛物线的对称轴l上的一点，在抛物线上是否存在点P，使△POF成为以点P为直角顶点的的等腰直角三角形．若存在，求出所有符合条件的点P的坐标，若不存在，请说明理由．3．如图，已知二次函数的图象经过点A （4，4）、B （5，0）和原点O ．P 为二次函数图象上的一个动点，过点P 作x 轴的垂线，垂足为D （m ，0），并与直线OA 交于点C ．（1）求出二次函数的解析式；（2）当点P 在直线OA 的上方时，求线段PC 的最大值；（3）当m ＞0时，探索是否存在点P ，使得△PCO 为等腰三角形，如果存在，求出P 的坐标；如果不存在，请说明理由．4．已知顶点为()1,5A 的抛物线2y ax bx c =++经过点()5,1B .（1）求抛物线的解析式；（2）设C ，D 分别是x 轴、y 轴上的两个动点.△当四边形ABCD 的周长最小时，在图1中作直线CD ，保留作图痕迹.并直接写出直线CD 的解析式；△点()(),0P m n m >是直线y x =上的一个动点，Q 是OP 的中点，以PQ 为斜边按图2所示构造等腰Rt PQR ∆.在△的条件下，记PQR ∆与COD ∆的公共部分的面积为S .求S 关于m 的函数关系式，并求S 的最大值.5．已知抛物线y＝a（x﹣1）（x﹣3）（a＜0）的顶点为A，交y轴交于点C，过C作CB△x 轴交抛物线于点B，过点B作直线l△x轴，连结OA并延长，交l于点D，连结OB．（1）当a＝﹣1时，求线段OB的长．（2）是否存在特定的a值，使得△OBD为等腰三角形？若存在，请写出求a值的计算过程；若不存在，请说明理由．（3）设△OBD的外心M的坐标为（m，n），求m与n的数量关系式．6．如图，抛物线y＝ax2+bx﹣4a（a≠0）经过A（﹣1，0）、C（0，4）两点，与x轴交于另一点B，连接AC，BC．（1）求抛物线的解析式；（2）过点C作x轴的平行线交抛物线于另一点D，连接BD，点P为抛物线上一点，且△DBP＝45°，求点P的坐标；（3）在抛物线的对称轴上是否存在点M，使得由点M，A，C构成的△MAC是直角三角形？若存在，求出点M的坐标；若不存在，请说明理由．7．如图，二次函数y=x2+bx+c的图像与x轴交于A，B两点，B点坐标为(4,0)，与y 轴交于点C(0,4).点D为抛物线上一点(1)求抛物线的解析式及A点坐标；(2)若△BCD是以BC为直角边的直角三角形时，求点D的坐标；(3)若△BCD是锐角三角形,请直接写出点D的横坐标m的取值范围.8．已知：如图，抛物线y＝ax2+bx﹣3与x轴交于A点，与y轴交于C点，且A（1，0）、B（3，0），点D是抛物线的顶点．（1）求抛物线的解析式（2）在y轴上是否存在M点，使得△MAC是以AC为腰的等腰三角形？若存在，求出点M的坐标；若不存在，请说明理由．（3）点P为抛物线上的动点，且在对称轴右侧，若△ADP面积为3，求点P的坐标．9．如图，抛物线y＝ax2+bx+3交x轴于点A（﹣1，0）和点B（3，0），与y轴交于点C．（1）求抛物线的解析式；（2）连接BC，若点P为线段BC上的一个动点（不与点B、点C重合），过点P作直线PN△x 轴于点N ，交抛物线于点M ，当△BCM 面积最大时，求△BPN 的周长． （3）在（2）的条件下，当△BCM 面积最大时，在抛物线的对称轴上是否存在点Q ，使△CNQ 为等腰三角形？若存在，请求出点Q 的坐标；若不存在，请说明理由．10．如图1，抛物线243y x x =++与x 轴交于,A B 两点（点A 在点B 左侧），与y 轴交于点C ，点D 抛物线的顶点.（1）求直线BD 的解析式；（2）抛物线对称轴交x 轴于点E ，P 为直线BD 上方的抛物线上一动点，过点P 作PF BD ⊥于点F ，当线段PF 的长最大时，连接PE ，过点E 作射线EM ，且EM EP ⊥，点G 为射线EM 上一动点（点G 不与点E 重合），连接PG ，H 为PG 中点，连接AH ，求AH 的最小值；（3）如图2，平移抛物线，使抛物线的顶点D 在射线BD 上移动，点B ，D 平移后的对应点分别为点'B ，'D ，y 轴上有一动点M ，连接'MB ，'MD ，''MB D ∆是否能为等腰直角三角形？若能，请求出所有符合条件的M 点的坐标；若不能，请说明理由.11．如图1，抛物线()230y ax bx a =++≠与x 轴交于()1,0A -、()30B ，两点，与y 轴交于点C ，顶点为点M ．（1）求这条抛物线的解析式及直线BM 的解析式；（2）P 段BM 上一动点（点P 不与点B 、M 重合），过点P 向x 轴引垂线，垂足为Q ，设OQ 的长为t ，四边形PQAC 的面积为S ．求S 与t 之间的函数关系式及自变量t 的取值范围；（3）在线段BM 上是否存在点N ，使NMC ∆为等腰三角形？若存在，请直接写出点N 的坐标；若不存在，请说明理由．12．如图,已知抛物线与x 轴交于A(−1,0)、B(3,0)两点,与y 轴交于点C(0,3).(1)该抛物线的对称轴是直线___________， (2)求抛物线的解析式；(3)设抛物线的顶点为D ，在其对称轴的右侧的抛物线上是否存在点P ，使得△PDC 是等腰三角形?若存在，求出符合条件的点P 的坐标；若不存在，请说明理由：13．在平面直角坐标系中，将二次函数()20y ax a =>的图象向右平移1个单位，再向下平移2个单位，得到如图所示的抛物线，该抛物线与x 轴交于点A 、B (点A 在点B 的左侧)，1OA =，经过点A 的一次函数()0y kx b k =+≠的图象与y 轴正半轴交于点C ，且与抛物线的另一个交点为D ，ABD ∆的面积为5．(1)求抛物线和一次函数的解析式；(2)抛物线上的动点E 在一次函数的图象下方，求ACE ∆面积的最大值，并求出此时点E 的坐标；(3)若点P 为x 轴上任意一点，在(2)的结论下，求35PE PA +的最小值．14．如图，抛物线2y ax bx c =++与x 轴的交点分别为()6,0A -和点()4,0B ，与y 轴的交点为()0,3C ．（1）求抛物线的解析式；（2）点P 是线段OA 上一动点（不与点A 重合），过P 作平行于y 轴的直线与AC 交于点Q ，点D 、M 在线段AB 上，点N 在线段AC 上．△是否同时存在点D 和点P ，使得APQ ∆和CDO ∆全等，若存在，求点D 的坐标，若不存在，请说明理由；△若DCB CDB ∠=∠，CD 是MN 的垂直平分线，求点M 的坐标．15．如图，抛物线y=ax 2+bx+2交x 轴于点A(-3，0)和点B(1，0)，交y 轴于点C (1)求这个抛物线的函数表达式．(2)点D 的坐标为(-1，0)，点P 为第二象限内抛物线上的一个动点，求四边形ADCP 面积的最大值．(3)点M 为抛物线对称轴上的点，问：在抛物线上是否存在点N ，使△MNO 为等腰直角三角形，且△MNO 为直角？若存在，请直接写出点N 的坐标；若不存在，请说明理由．16．如图，抛物线23y ax bx =+-与x 轴交于(1,0)A -，(3,0)B 两点，与y 轴交于点C ，点D 是抛物线的顶点．（1）求抛物线的解析式．（2）点N 是y 轴负半轴上的一点，且ON =Q 在对称轴右侧的抛物线上运动，连接QO ，QO 与抛物线的对称轴交于点M ，连接MN ，当MN 平分OMD ∠时，求点Q 的坐标．（3）直线BC 交对称轴于点E ，P 是坐标平面内一点，请直接写出PCE ∆与ACD ∆全等时点P 的坐标．17．已知：直线122y x =+与y 轴交于A ，与x 轴交于D ，抛物线y ＝12x 2+bx +c 与直线交于A 、E 两点，与x 轴交于B 、C 两点，且B 点坐标为 （1，0）．（1）求抛物线的解析式；（2）点P 是直线AE 上一动点，当△PBC 周长最小时，求点P 坐标； （3）动点Q 在x 轴上移动，当△QAE 是直角三角形时，求点Q 的坐标；（4）在y 轴上是否存在一点M ，使得点M 到C 点的距离与到直线AD 的距离恰好相等？若存在，求出所有符合条件的点M 的坐标；若不存在，请说明理由．18．如图，已知抛物线y ＝x 2+bx +c 与x 轴交于点A ，B ，AB ＝2，与y 轴交于点C ，对称轴为直线x ＝2．（1）求抛物线的函数表达式；（2）设D 为抛物线的顶点，连接DA 、DB ，试判断△ABD 的形状，并说明理由； （3）设P 为对称轴上一动点，要使PC ﹣PB 的值最大，求出P 点的坐标．19．如图，抛物线2y ax bx c =++ 经过点()2,5A -，与x 轴相交于()1,0B -，()3,0C 两点，（1）抛物线的函数表达式；（2）点D 在抛物线的对称轴上，且位于x 轴的上方，将BCD ∆沿沿直线BD 翻折得到BC D '∆，若点D '恰好落在抛物线的对称轴上，求点C '和点D 的坐标；（3）设P 是抛物线上位于对称轴右侧的一点，点Q 在抛物线的对称轴上，当CPQ ∆为等边三角形时，求直线BP 的函数表达式.20．如图，在直角坐标系中有Rt AOB ∆，O 为坐标原点，1,tan 3OB ABO =∠=，将此三角形绕原点O 顺时针旋转90︒，得到Rt COD ∆，二次函数2y x bx c =-++的图象刚好经过,,A B C 三点．（1）求二次函数的解析式及顶点P 的坐标；（2）过定点Q 的直线:3l y kx k =-+与二次函数图象相交于,M N 两点． △若2PMN S ∆=，求k 的值；△证明：无论k 为何值，PMN ∆恒为直角三角形；△当直线l 绕着定点Q 旋转时，PMN ∆外接圆圆心在一条抛物线上运动，直接写出该抛物线的表达式．参考答案：1．（1）B （0，2），抛物线解析式为y=﹣43x 2+103x+2；（2）m 的值为12；（3）当以B ，P ，N 为顶点的三角形与△APM 相似时，点M 的坐标为（2.5.0）或（118，0）． 2．（1）B （3m ，0）；（2）tan△ACB ＝12；（3）点P 的坐标是：）或）． 3．（1）y ＝﹣x 2+5x ；（2）当点P 在直线OA 的上方时，线段PC 的最大值是4；（3）存在，P 的坐标是（4，2﹣）或（6，﹣6）或（5，0）． 4．（1）()21154y x =--+；（2）；4y x =-+；△S 27448x x =-+-；S 的最大值为47.5．（1）5；（2）a ＝﹣1（3）m ＝3n 2+2 6．（1）y ＝﹣x 2+3x +4；（2）P （﹣25，6625）；（3）点M 的坐标为（32，298）或（32，﹣58）或（32，52）或（32，32）．7．(1)y=x 2-5x+4, A(1,0)；(2)(6,10)或(2,-2)；m ＜6或 3m ＜28．（1）y ＝﹣x 2+4x ﹣3；（2）在y 轴上存在点M ，点M 的坐标为(0,3)，(0,3-或(0,3-，（3）P （4，﹣3）．9．（1）y ＝﹣x 2+2x+3 （2）310．（1）43y x =-+（2（3）(0,,,.11．（1）2y x 2x 3=-++，26y x =-+；（2）四边形ACPQ S 29322t t =-++，t 的取值范围是13t <<；（3）716,55N ⎛⎫⎪⎝⎭或14N ⎛ ⎝⎭或()2,2N 12．（1）1x = （2）2y x 2x 3=-++；（3）存在，⎝⎭或（2.3）13．(1)21322y x x =--；1122y x =+；(2)ACE ∆的面积最大值是2516，此时E 点坐标为315,28⎛⎫- ⎪⎝⎭；(3)35PE PA +的最小值是3.14．（1）211384y x x =--+；（2）△存在点D ，使得APQ ∆和CDO ∆全等，3,02D ⎛⎫⎪⎝⎭，理由见解析；△点3,02M ⎛⎫⎪⎝⎭15．(1)y=-23x 2-43x+2；(2)S 的最大值为174；(3)存在，点N或)或)或)．16．（1）223y x x =--；（2）点Q 的坐标为：1Q ，2Q ；（3）若PCE ∆与ACD ∆全等，P 点有四个，坐标为1(3,4)P --，2(1,6)P --，3(2,1)P ，4(4,1)P -． 17．（1）215222y x x =-+；（2）P （1213，3213）；（3）Q 点坐标为（1，0）或（172，0）；（4）存在；M 点坐标为M （0，﹣8）.18．（1）抛物线的函数表达式为y ＝x 2﹣4x +3；（2）△ADB 是等腰直角三角形；理由见解析；（3）P （2，﹣3）．19．（1）223y x x =--；（2）点'C 坐标为(点D 的坐标为⎛ ⎝⎭；（3）直线BP 的函数表达式为y =y x =20．（1）2y x 2x 3=-++,()1,4P ;（2）△k =±△2241y x x =-++．。

今天讲解二次函数背景下的四边形存在性问题．这里的四边形存在性问题，一般是以几种特殊的四边形为主，常考察的有平行四边形、菱形、 矩形、正方形．当然，三角形的存在性问题和四边形的存在性问题是一样， 如等腰三角形实际上和 菱形是一致的， 直角三角形和矩形是一样的， 等腰直角三角形和正方形是一致的．本文我们将重点讲解这类问题的求解逻辑以及注意事项，同时给大家理出一个比较通用的解题 模板．1如图，抛物线y = ax 2 + bx + 3 交x 轴于点A (−1, 0) 和点B (3, 0) ，与 y 轴交于点C ，连接BC ， 交对称轴于点D ．(1) 求抛物线的解析式；(2)点 P 是直线BC 上方的抛物线上点，连接PC ，PD ．求 △PCD 的面积的最大值以及此时 点P 的坐标；(3)将抛物线y = ax 2 + bx + 3 向右平移 1 个单位得到新抛物线，新抛物线与原抛物线交于点E ， 点F 是新抛物线的对称轴上的一点，点 G 是坐标平面内一点．当以D 、E 、F 、 G 四点为顶点的 四边形是菱形时，直接写出点F 的坐标，并写出求解其中一个点F 的坐标的过程．前两小问就不详说了，直接上结论， 抛物线解析式为y = −x 2 + 2x + 3 ；点 P | , | ．( 3 15 )\2 4 )第 3 小问为菱形存在性问题， 以D 、E 、F 、 G 四点为顶点的四边形是菱形．四个点中， D ， E 是定点，F 是平移后新抛物线对称轴上的动点，由于点F 的横坐标是确定的，只有纵坐标在变化， 我们可以称其为“G 如果只需要点F 的坐标，那么没有必要求解平移后抛物线的解析式．根据平移的性质，将原抛物线 向右平移 1 个单位长度， 那么原抛物线的对称轴也向右平移 1 个单位长度， 因此新抛物线的对称轴 为x = 2 ，几 F (2, m ) ．但由于此时E 为量抛物线的交点，因此还是要把平移后的抛物线解析式求出 来，根据“左加右减”，平移后的抛物线解析式为y = − (x −1)2+ 2(x −1) + 3 = −x 2 + 4x ，联立两抛物(|y = −x 2 + 2x + 3 ( 3 15 ) 线〈|ly = −x 2 + 4x ，解得E |\2 , 4 )| ．菱形的探究相对是比较简单的，对于这类探究性问题，一般都是先从确定的信息入手．菱形是 以D 、E 、F 、 G 为顶点， 其中DE 为定线段，那么存在的可能有DE 是一条边，也可能是一条对 对角线．前面提到，等腰三角形和菱形的分析是一致的，这里我们结合等腰三角形的存在性问题一 起分析．由于 G 是“自由点”，可以随机应变，因此讨论以D 、E 、F 为顶点的三角形是等腰三角 形．同样， 由于定线段DE 可能是等腰三角形的一条腰，也可能是底边．当DE 为一条腰时，第一种情形是点D 为顶点，即DE = DF ，也即半动点F 到D 的距离和E 到D 的距离相等，因此点F 在以点D 为圆心， DE 为半径的圆上，作出该圆，如图 1 所示，可知此时圆与新抛物线的对称轴有两个交点F 1 ，F 2 ，结合图象可以判断，此时两个点应该都是满足的．那么 再加上对应的“自由点” G ，就是以DE 为边菱形了．当DE 为一条腰时， 另一种情形是点E 为顶点， 即ED = EF ，也即半动点F 到E 的距离和D 到E 的距离相等，因此点F 在以点E 为圆心， ED 为半径的圆上，作出该圆，如图 2 所示，可知此时 圆与新抛物线的对称轴同样有两个交点F 1 ，F 2 ，结合图象， 此时的F 3 存在和DE 共线的风险，因此后续需要检验一下．根据坐标可以知道，x E =，通常像这类圆心可能为两个点中点的，一般都要留个心眼， 检验一下．此时再加上对应的“自由点” G ，也是以DE 为边菱形．当DE 为底边时，则F 为顶点， 即FD = FE ，即 F 到线段DE 的两端点的距离相等，可知此时F 在线段DE 的垂直平分线上，作出线段DE 的垂直平分线，如图 3 所示，可知此时有一个交点F 5 ．加 上对应的“自由点” G ，此时便是以DE 为对角线的菱形．对于等腰三角形和菱形的存在性问题，如上图情形，我们称其为“两圆一线”法．由于这类题一般不需要书写完整过程，因此在解题过程中，把准备工作做好， 即对应的点坐标， 解析式等先求出来， 动点坐标假设好， 再把定线段DE ，半定线段DF 、EF 长度表示出来． 根据上 述分析，结合“两圆一线”分别使得三条线段两两相等建立方程，即DE = DF ，DE = EF ，DF = EF ， 求解出动点坐标即可．(实际解题过程中， 一般使用线段平方的形式．此外， 只需关注下方解析中公 式计算部分即可，文字叙述部分可忽略)此题还是比较友善的，只需求出F 坐标．如果需要求解点G 的坐标，则还要加一个步骤．这里 以DEG 1F 1 为例，若要求 G 1 坐标，一般有两种比较常用的思路．一是利用菱形的对边平行且相等，即F 1G 1 可以看成是DE 平移得来的， 那么点D → F 1 的平移变化也即点E → G 1 的平移变化． 二是利用菱形的对角线相互平分，因此EF 1 的中点也即DG 1 的中点，利用中点坐标求解出 G 1 坐标．这两种处理 在平行四边形存在性问题中也是有力手段．(|y = −x 2 + 2x + 3 ( 3 15 ) 149 ( 149 )由题， y = −x 2 + 2x + 3 向右平移 1 个单位得到新抛物线y = − (x −1)2+ 2(x −1) + 3 = −x 2 + 4x ，联立〈|ly = −x 2 + 4x ，解得 E |\2 , 4 )| ， 新抛物线的对称轴为x = 2 ，设 F (2, m ) ，由于 D (1, 2) ，则DE 2 =，EF 2 = + m −2= m 2 − m +，DF 2 = 1+ (m − 2)2= m 2 − 4m + 5 ，①当DE 、DF 为一组邻边时，则 DE 2 = DF 2 ，即 = m 2 − 4m + 5 ，37 ( ) ( )②当ED 、EF 为一组邻边时，则 ED 2 = EF 2 ，即 = m 2 − m + ，16 8 16 11 ( 11)③当EF 为对角线时，则FD = FE ，即 m 2 − m + = m 2 − 4m + 5 ， 2 16解得m = ，此时 F 的坐标为|2, | ；( ) ( ) ( 149 )( 11) 当F |2, |时， y F + y D = 2y E ，x D + x F = 2x E ，即 E 为D 、F 中点， 不合题意， 舍去； 15 229 \ 2 )综上， F 点的坐标为||\2, 2 + 4 )|| 或||\2, 2 − 4 )|| 或(2, 2) 或|\2, 56 )| ． 56 \ 56 )解得m = 2 或m = ，此时F 的坐标为(2, 2) 或|2, | ，2 \ 2 )解得m = 2 土 4 ，此时 F 的坐标为||\2, 2 + 4 )|| 或||\2, 2 − 4 )|| ；53 15 2291 ．已知二次函数y = ax2 + bx − 2(a 丰 0)与x 轴交于A ( −, 0) ，B (4, 0) ，与 y 轴交于点C ．(1) 求抛物线的解析式；(2) 连接AC ，BC ，点 P 是直线BC 下方抛物线上一点，过 P 作PD ∥AC 交直线BC 于点D ，PE ∥x 轴交直线BC 于点， E ，求△PDE 面积的最大值及此时点， P 的坐标；(3) 在(2)的条件下， 将原抛物线沿x 轴向左平移3个单位得到新抛物线，点 M 是新抛物线对称轴上一点， 点 N 是平面直角坐标系内一点， 当以点M 、 N 、P 、B 为顶点的四边形为菱形 时，请直接写出所有符合条件的N 点的坐标；并任选其中一个N 点，写出求解过程．立〈y= − 2 x 2 + 4x − 2 ，解得D 7 , 11 ．1-1如图 1，抛物线y = ax 2 + bx + 4 交x 轴于A (−2, 0) ，B (4, 0) 两点，与y 轴交于点C ，连接 AC ， BC ．(1) 求抛物线的解析式；(2) P 是拋物线上位于直线BC 上方的一个动点，过点P 作PQ ∥y 轴交BC 于点Q ， 过点P 作PE ⊥ BC 于点E ，过点 E 作EF ⊥ y 轴于点F ，求出2PQ + EF 的最大值及此时点P 的坐标；(3)如图 2，将抛物线y = ax 2 + bx + 4 沿着射线CB 的方向平移，使得新抛物线y ，过点(3,1) ， 点D 为原抛物线y 与新抛物线y ，的交点，若点 G 为原抛物线的对称轴上一动点，点H 为新抛物线y ， 上一动点，直接写出所有使得以 A ，D ， G ，H 为顶点的四边形为平行四边形的点H 的坐标，并 把求其中一个点H 的坐标的过程写出来．抛物线解析式为y = − x 2 + x + 4 ；点 P | , | ．相当于是沿着射线BC 方向平移，故舍去， 因此可得平移后抛物线的解析式为y = − x 2 + 4x − ．联2 2 ( 1 13 y = − x 2 + x +4 \2 8 )这类平行四边的探究也并不难， 同样先从确定的信息入手．平行四边形是以A ，D ，G ，H 为 顶点，其中AD 是定线段， G 是半动点，H 在新的抛物线上．和菱形的讨论一样，我们要考虑AD 是 一条边的情形， 也要考虑AD 是对角线的情形．当 AD 是一条边时， 实际上此时也右两种情形，一是是平行四边形为ADHG ，也即AH ，DG 为 对角线；另一种则是平行四边形为ADGH ，也即 AG ，DH 为对角线．当然，不管是那种情形，由 于 AD 是一条边，根据平行四边形对边平行且相等的性质， GH 这条边可以看作是将AD 平移后得到1 (8 28 )2 \3 9 )第 3 小问中， 抛物线沿着射线CB 方向平移， 由于后续的点在新抛物线上， 因此还是要求出平移 后抛物线的解析式．这类沿着射线平移的，一般采用正交分解的形式平移，由点 C (0, 4) ，B (4, 0) 可 知，沿着射线 CB 平移，即向右平移t 个单位，则向下也平移t 个单位，因此假设平移后新抛物线的 解析式为y = − (x − t )2+ (x − t ) + 4 − t ，因为平移后经过点(3,1) ，代入可解得t = − 1 或t = 3 ，当 t = − 1 ， 1 13的，由于半动点 G 在原抛物线对称轴x = 1 上，那么点 G 有可能是点 A 平移后得到的， 此时点H 就 是点D 平移后得到的，如图 1 所示；同理，当点 G 是点D 平移后得到的，那么此时点H 就是点A 平 移后得到的，如图 2 所示．设点 G (1, m )，根据平移的性质，结合点坐标的变化规律，当 A → G 时， 即(−2, 0) —(1, m ) ，则有D|2 , 8 )| —H | 2 , 8 + m )| ，由于点H 在新抛物线上， 且横坐标已知了，代入新抛物线即可 11 1 (13 213 13 13 (13 13 此外， 除了用平移性质得到H 点的坐标外，此时 AH 是一条对角线，也利用对角线相互平分， 则 A 、 H 的 中 点 和 D 、 G 的 中 点 是 同 一 个 ， 利 用 中 点 坐 标 则 有 x A + x H = x D + x G ，故 13 13 13 (13 13 x H = x D + x G − x A = 2 ，将x = 2 代入新抛物线解析式，可求得H 点纵坐标y = − 8 ，故H | 2 , − 8 )|．当 AG 是一条对角线时， 则有x A + x G = x D + x H ，故 x H = x A + x G − x D = − ，代入新抛物线解析 277 ( 9 277式，可求得此时H 的纵坐标为 − ，故H |− , − | ．8 2 8 ) 当 AD 是一条对角线时，则有x A + x D = x H + x G ，故 x H = x A + x D − x G = ，代入新抛物线解析式， 37 ( 1 37 可求得此时H 的纵坐标为 − ，故 H | , − | ．8 2 8 )同样地，在解题过程中， 把准备工作做好，即对应的点坐标，解析式等先求出来，动点坐标假设好， 将点坐标表示列出来(通常都是横坐标)，选定一个定点，如这里我们选定 x A ，将其与剩下 三点横坐标x D 、x G 、x H 两两组合，建立中点坐标关系式， 即x A + x D = x H + x G ，x A + x G = x D + x H 以 及x A + x H = x D + x G ，求解出点H 横坐标，再代入解析式中求出点H 纵坐标即可．求得纵坐标 8 + m = − 2 | 2 )| + 4 2 − 2 = − 8 ，此时H | 2 , − 8 )| ． ( 7 11 (13 1113 (13 13)由题， 设平移后的抛物线解析式为y = − (x − t )2+ (x − t ) + 4− t ，因为平移后经过点(3,1)，代入可解得t = − 1 (舍) 或t = 3 ，2 2联立〈y = − 2 x 2 + 4x − 2 ，解得 D 7 , 11 ， y = − x 2 + x + 4 \2 8 )则x A =−2 ，x D = ，x G = 1，设 H 点横坐标为x H ，①当AH 为一条对角线时，x A + x H = x D + x G ，则 x H = ，代入可求得此时H | , − | ； 9 ( 9 277 )1 (1 37 )综上， H 的坐标为| , − |或|− , − |或| , − | ．( 1 13 ③当AD 为一条对角线时，x A + x D = x H + x G ，则x H = ，代入可求得此时H | , − | ；(13 13) ( 9 277 ) (1 37 )2 \2 8 )\ 2 8 ) \ 2 8 ) \2 8 )②当AG 为一条对角线时，x A + x G = x D + x H ，则x H = − ，代入可求得此时H |− , − | ；2 \ 2 8 ) 2 \ 2 8 )故平移后抛物线的解析式为y = − x 2 + 4x − ，1 131．如图，在平面直角坐标系中，抛物线y= ax2 + bx+ 3(a 0) 与y轴交于点C，与x轴交于A，B两点(点A在点B的右侧)，且点A的坐标为( 3, 0) ，连接BC，过点A作AD∥BC交y轴于点D，OB= 3OA．(1) 求抛物线的解析式；(2) 如图1，点E为射线AD上一点，点P为第二象限内抛物线上一点，求四边形PBEC面积的最大值及此时点P的坐标；(3) 如图2，将原抛物线沿x轴正方向平移得到新抛物线y，y经过点C，平移后点A的对应点为点A，点N为线段AD的中点，点Q为新抛物线y的对称轴上一点，在新抛物线y上存在一点M，使以点M，Q，A，N为顶点的四边形为平行四边形，请直接写出点M的坐标，并选择一个你喜欢的点写出求解过程．2．如图，抛物线y= x2 + bx+ c与x轴相交于点A(−1, 0) 和点B，交y轴于点C，tan 三ACO= ．(1) 求抛物线的解析式；(2) 如图1 ，P点为一象限内抛物线上的一个动点，点D是BC中点，连接PD，BD，PB．求△BDP面积的最大值以及此时P点坐标；，M为新抛物线对称轴上(3) 如图2，将抛物线向左平移 1 个单位长度，得到新的抛物线y1一点，N为直线AC上一动点，在(2) 的条件下，是否存在点M，使得以点P、B、M、N为顶点的四边形为平行四边形？若存在，请直接写出点N的坐标；若不存在，请说明理由．| 4 21如图，已知抛物线y = ax 2 + bx − 4 与x 轴交于A ，B 两点， 与y 轴交于点C ，且点A 的坐标 为(−2, 0) ，直线BC 的解析式为y = x − 4 ．(1) 求抛物线的解析式；(2)如图 1，过点 A 作 AD ∥BC 交抛物线于点D (异于点 A )， P 是直线BC 下方抛物线上一 点，过点P 作PQ ∥y 轴， 交AD 于点Q ，过点 Q 作QR ⊥ BC 于点R ，连接PR ．求△PQR 面积的最 大值及此时点P 的坐标；(3) 如图 2，点 C 关于x 轴的对称点为点C ，将抛物线沿射线 C A 的方向平移2个单位长度得到新的抛物线y ，新抛物线y 与原抛物线交于点M ，原抛物线的对称轴上有一动点 N ，平面直 角坐标系内是否存在一点K ，使得以 D ，M ，N ，K 为顶点的四边形是矩形？若存在，请直接写 出点K 的坐标；若不存在， 请说明理由．抛物线解析式为y = x 2 − x − 4 ；S △PQR 的最大值为 9，点P (4, −6) ．第 3 小问中，抛物线沿着射线C A 方向平移， 由于点M 为两抛物线交点， 因此需求出平移后抛 物线的解析式．根据A (−2, 0) ，C (0, 4) ，可知Rt △AOC 中AO : OC : AC = 1: 2 : ，因此将抛物线沿着射线C A 方向平移2个单位长度，则相当于向下平移 4 个单位长度，向左平移 2 个单位长度，因此平移后的抛物线为y = 1 (x + 2)2− 3 (x + 2) − 4 − 4 = 1 x 2 − 1 x −10 ，联立〈y = x 2 − x −10，解4 2 4 2y = x 2 − x − 4( 1得M (6, −4) ．又 BC : y = 1 x − 4 ，可知 AD : y = 1 x + 1，联立〈 y = 2 x + 1，解得D (10, 6) ．2 2 |y = 1 x 2 − 3x − 4因为以D ，M ，N ，K 为顶点的四边形是矩形，此时定线段是DM ，半动点为N ，自由点为K ．和 前面讨论菱形、平行四边形时的流程基本大同小异，定线段DM 可能是矩形的边，也可能是矩形的 对角线，因此要分两种情形讨论．矩形的存在性问题和直角三角形的存在性问题是一致的，如本题 中，探究以D ，M ，N 为顶点的三角形是直角三角形． 同样地，先以直角三角形为例，那么D ，M ，1 3 4 2在实际解题中设 K (x , y ) 即可)， 利用中点关系〈 M K D N ，则〈 K，整理得N 均有可能为直角顶点．当M 为直角顶点时，过M 作DM 垂线与对称轴交点即为点N 所在位置，如图 1 所示．对于N 点 坐标的求解，一方面，由于MN ⊥ DM ，则 k MN . k DM = − 1，结合点M 坐标，由此可求得直线MN 解 析式，将其与对称轴方程联立即可求得点N 坐标．另一方面，可以构造如图所示的K 型相似，即构DH MH1 腰直角三角形， 或者四边形中的正方形， 那么可以构造此类的K 型全等求解．在此直角三角形的基础上，加上自由点K ，就变成矩形问题了．对于矩形问题，同样可以求出点N 坐标后，利用平移关系或者对角线的中点关系，求相应的点K 的坐标．当然，如果是探究矩形 的存在性问题，也可以直接利用中点关系求得点K 的坐标．由点N (3, n )，设K (x K , y K ) (熟练后，(x + x = x + x (6 + x = 10 + 3 l y M + y K = y D + y N l−4 + y K = 6 + n 〈，再由对角线相等，即MK = DN ，代入即有1+ (y + 4)2= 49 + (16 − y )2，解得 y =，( 36 )同样适用．当D 为直角顶点时，三角形如图2 所示．同样， 加上自由点K ，就变成矩形问题了． 这里我们5 2 2 ( 44 )l y M + y N = y D + y K |y K = − \ 5 )对于直角三角形或矩形问题， 如上图情形，我们可以称其为“两线一圆”．若只求点N 坐标，一 般利用斜率关系，求出解析式后进一步求解．如果是矩形问题要求自由点的坐标，可以用对角线平 分且相等， 建立方程求解．当然， 先求点N ，利用点N 作为台阶进一步求解也是没问题的， 大家选 用自己顺手的方法即可．造 △MN 1G ∽△DMH ，利用 = ，可求出长度，进而得到点 N 坐标．更特殊地，如果是等以垂线方式求解．由于k DM = 2 ，则 k DN = − 5 ，故此时DN : y = − 5 x + 10 ，令x = 3 ，可解得N |\3, 5 )| ， 由中点可知，〈(x M + x N = x D + x K ，可解得〈(|x K = − 16 ，此时 K −1,− 6 ．l 5当N 为直角顶点时，则有NM ⊥ ND ，因此点N 在以DM 为直径的圆上．此种情形若只是求点N 坐标，策略比较多， 一方面，可以利用斜率， 由k ND . k NM= − 1求出点N 坐标；另一方面，可以利用线段长度求解，设DM 中点为为R ，则此时圆心为R ，因此NR = RD = DM ，由此也可求得点N 坐 标， 此外， 还可以利用勾股定理ND 2 + NM 2 = DM 2 ．当加入自由点K ，变成矩形问题后，除了先求 出点N 坐标， 利用平移或中点求解点K 坐标外，也可以利用前面的对角线平分且相等来求解． 故此时K |7, | ．此法借助的是矩形的对角线平分且相等的性质，该处理对于DM 是对角线的情形 \ 5 ) GM N G式和长度关系式子，即〈 M K D N 且MK 2 = DN 2 ，〈 M N D K 且MN 2 = DK 2 以及(x M + x D = x N + x K 4 2 4 2|l 4 2(x M + x K = x D + x N (6 + x = 10 + 3 (x = 7由MK 2 = DN 2 ，代入即有1+ (y + 4)2= 49 + (16 − y )2，解得 y = 36，故此时K 7,36；由MN 2 = DK 2 ，代入即有9 + (y +14)2 = 121+ (y − 6)2，解得 y = − 6 ，故此时K −1,− 6 ；(x M + x D = x N + x K (6 + 10 = 3 + x (x = 13 同样地，在解题过程中， 把准备工作做好，即对应的点坐标安排到位，动点坐标假设好，选定 一个定点， 如这里我们选定M ，将其与剩下三点横坐标D 、 N 、K 两两组合， 建立中点坐标关系 (x + x = x + x (x + x = x + xl y M + y K = y D + y N l y M + y N = y D + y K〈 且MD 2 = NK 2，利用方程组求解出对应的点K 的坐标． l y M + y D = y N + y K附：坐标平面内点A (x 1 , y 1 ) ，B (x 2 , y 2 ) ，其中x 1 丰 x 2 ，则过A 、B 两点的直线的斜率k =由题， 将抛物线沿着射线 C ,A 方向平移2个单位长度， 即将其向下平移 4 个单位长度， 向左平移 2 个单位长度， 因此平移后的抛物线为y =1(x + 2)2 − 3 (x + 2) − 4 − 4 = 1 x 2 − 1 x −10 ， 联立〈y = x 2− x −10，解得M (6, −4) ，y = x 2 − x − 4( 1又 BC : y = 1 x − 4 ，可知 AD : y = 1 x + 1，联立〈 y = 2 x + 1，解得D (10, 6) ，2 2 |y = 1 x 2 − 3x − 4由M (6, −4) ，D (10, 6) ，设 N (3, n ) ，K (x , y ) ，①当MK 为一条对角线时，〈，即〈 ，整理得〈 ， l y M + y K = y D + y N l −4 + y = 6 + n l n = y −105 \ 5 )②当MN 为一条对角线时，〈(x M + x N = x D + x K，即〈(6 + 3 = 10 + x，整理得〈(x = − 1l y M + y N = y D + y K l −4 + n = 6 + y l n = 10 + y5 \ 5 )③当MD 为一条对角线时，〈 ，即〈 ，整理得〈l y M + y D = y N + y K l−4 + 6 = n + y l n = 2 − y由MD 2 = NK 2 ，代入即有116 = 100 + (2 − 2y )2，解得y =− 1 或y = 3 ，故此时K (13, −1) 或(13,3) ； ( 36 ) ( 6 )综上， 点K 的坐标为|7, |或|−1,− |或(13, −1) 或(13,3) ．\ 5 ) \ 5 ) y 1 − y 2． x 1 − x 21．如图1，二次函数y= ax2 + bx+ c(a丰0)与x轴交于点A(−2, 0) 、点B(点A在点B左侧)，与y轴交于点C(0,3) ，tan 三CBO= ．(1) 求二次函数解析式；(2)如图2，点P是直线BC上方抛物线上一点，PD∥y轴交BC于D，PE∥BC交x轴于点E，求PD+ BE的最大值及此时点P的坐标；(3) 在(2) 的条件下，当PD+ BE取最大值时，连接PC，将△PCD绕原点O顺时针旋转90。

二次函数中的十二大存在性问题【题型1二次函数中等腰三角形的存在性问题】【题型2二次函数中直角三角形的存在性问题】【题型3二次函数中等腰直角三角形的存在性问题】【题型4二次函数中全等三角形的存在性问题】【题型5二次函数中平行四边形的存在性问题】【题型6二次函数中菱形的存在性问题】【题型7二次函数中矩形的存在性问题】【题型8二次函数中正方形的存在性问题】【题型9二次函数中面积问题的存在性问题】【题型10二次函数中线段问题的存在性问题】【题型11二次函数中角度问题的存在性问题】【题型12二次函数中最值问题的存在性问题】【题型1二次函数中等腰三角形的存在性问题】1(2023春·甘肃张掖·九年级校考期中)如图甲，直线y=-x+3与x轴、y轴分别交于点B、点C，经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A，顶点为P．(1)求该抛物线的解析式；(2)当0<x<3时，在抛物线上求一点E，使△CBE的面积有最大值(图乙、丙供画图探究)，并求出最大面积及E点的坐标．(3)在该抛物线的对称轴上是否存在点M，使以C、P、M为顶点的三角形为等腰三角形？若存在，请求出所符合条件的点M的坐标；若不存在，请说明理由；1(2023春·广西贵港·九年级统考期末)如图，抛物线y=ax2+3x+c a≠0和与x轴交于点A-2,0点B，与y轴交于点C0,8，点P为直线BC上方抛物线上的动点，连接CP，PB，直线BC与抛物线的对称轴l交于点E．(1)求抛物线的解析式；(2)求△BCP的面积最大值；(3)点M是抛物线的对称轴l上一动点．是否存在点M，使得△BEM为等腰三角形？若存在，求出点M的坐标；若不存在，请说明理由．2(2023春·山西晋城·九年级校考期末)如图1，抛物线y=ax2+bx+3与x轴交于A-1,0两，B4,0点，与y轴交于点C，顶点为D．点P是直线BC上方抛物线上的一个动点，过点P作PE⊥x轴于点E，交直线BC于点Q．(1)求抛物线的表达式；(2)求线段PQ的最大值；(3)如图2，过点P作x轴的平行线交y轴于点M，连接QM．是否存在点P，使得△PQM为等腰三角形？若存在，请直接写出点P的横坐标；若不存在，请说明理由．3(2023•沙坪坝区校级模拟)如图1，抛物线y=ax2+bx+2(a≠0)交x轴于点A(-1，0)，点B(4，0)，交y轴于点C．连接BC，过点A作AD∥BC交抛物线于点D(异于点A)．(1)求抛物线的表达式；(2)点P是直线BC上方抛物线上一动点，过点P作PE∥y轴，交AD于点E，过点E作EG⊥BC于点G，连接PG．求△PEG面积的最大值及此时点P的坐标；(3)如图2，将抛物线y=ax2+bx+2(a≠0)水平向右平移32个单位，得到新抛物线y1，在y1的对称轴上确定一点M，使得△BDM是以BD为腰的等腰三角形，请写出所有符合条件的点M的坐标，并任选其中一个点的坐标，写出求解过程．【题型2二次函数中直角三角形的存在性问题】1(2023春·四川广安·九年级校考期中)如图，已知抛物线y=ax2+bx+c(a≠0)经过点A(-3,2)，B(0,-2)，其对称轴为直线x=52，C0,1 2为y轴上一点，直线AC与抛物线交于另一点D．(1)求抛物线的函数表达式；(2)试在线段AD下方的抛物线上求一点E，使得△ADE的面积最大，并求出最大面积；(3)在抛物线的对称轴上是否存在一点F，使得△ADF是直角三角形？如果存在，求点F的坐标；如果不存在，请说明理由．1(2023春·辽宁盘锦·九年级校考期中)如图，已知直线y=x+3与x轴交于点A，与y轴交于点B，抛物线y=-x2+bx+c经过A、B两点，与x轴交于另一个点C，对称轴与直线AB交于点E，抛物线顶点为D．(1)求抛物线的解析式；(2)在第三象限内，F为抛物线上一点，以A、E、F为顶点的三角形面积为3，求点F的横坐标；(3)点P是对称轴上的一动点，是否存在某一点P使P、B、C为顶点的三角形是以BC为直角边的直角三角形？若存在，请直接写出所有符合条件的P点坐标；不存在，说明理由．2(2023春·广东梅州·九年级校考期中)已知二次函数y=x2+bx+c的图象经过A(-2,5)，B(-1,0)，与x轴交于点C．(1)求这个二次函数的解析式；(2)点P直线AC下方抛物线上的一动点，求△PAC面积的最大值；(3)在抛物线对称轴上是否存在点Q，使△ACQ是直角三角形？若存在，直接写出点Q的坐标，若不存在，请说明理由．3(2023春·甘肃金昌·九年级统考期中)平面直角坐标系中，抛物线y=a(x-1)2+92与x轴交于A，B(4，0)两点，与y轴交于点C．(1)求抛物线的解析式，并直接写出点A，C的坐标；(2)在抛物线的对称轴上是否存在点P，使△BCP是直角三角形？若存在，请直接写出点P的坐标，若不存在，请说明理由；(3)如图，点M是直线BC上的一个动点，连接AM，OM，是否存在点M使AM+OM最小，若存在，请求出点M的坐标，若不存在，请说明理由；【题型3二次函数中等腰直角三角形的存在性问题】1(2023春·山西阳泉·九年级统考期末)综合与探究：在平面直角坐标系中，抛物线y=ax2+bx-2与x轴交于点A-1,0作平行于x轴的直线l，直线l与抛物线y，与y轴交于点C，过动点D0,m和点B4,0=ax2+bx-2相交于点E，F．(1)求抛物线的表达式；(2)求m的取值范围；(3)直线l上是否存在一点P，使得△BCP是以BC为直角边的等腰直角三角形？若存在，求m的值；若不存在，请说明理由．1(2023春·福建漳州·九年级校考期中)如图①，已知抛物线y=ax2+bx+3的图象经过点B1,0，与y 轴交于点A，其对称轴为直线l：x=2，过点A作AC∥x轴交抛物线于点C，∠AOB的角平分线交线段AC于点E，点P是抛物线上的一个动点，设其横坐标为m．(1)求抛物线的解析式；(2)若动点P在直线OE下方的抛物线上，连接PE、PO，当m为何值时，四边形AOPE面积最大，并求出其最大值；(3)如图②，F是抛物线的对称轴l上的一点，在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形？若存在，直接写出所有符合条件的点P的坐标；若不存在，请说明理由．2(2023春·湖南湘西·九年级统考期末)如图，在平面直角坐标系中，直线y =-x +3交x轴于点B ，交y 轴于点C ，直线AD 交x 轴于点A ，交y 轴于点D ，交直线BC 于点E -12，72，且CD =1．(1)求直线AD 解析式；(2)点P 从B 点出发沿线段BA 方向以1个单位/秒的速度向终点A 运动(点P 不与A ，B 两点重合)，设点P 的运动时间为t ，则是否存在t ，使得△AEP 为等腰直角三角形？若存在，请求出t 的值，若不存在，请说明理由；(3)在(2)的条件下，点P 出发的同时，点Q 从C 点出发沿射线CO 方向运动，当点P 到达终点时，点Q 也停止运动，连接AQ ，PQ ，设△APQ 的面积为S ，S 与t 的函数关系式为S =32t 2-12t +2120≤t <1a t -1 t -7 1<t <7，其图象如图2所示，结合图1、图2的信息，请求出a 的值及当△APQ 的面积取得最大值时AQ 的长．3(2023春·北京通州·九年级统考期末)如图，抛物线y1=ax2-2x+c的图象与x轴交点为A和B，与y 轴交点为D0,3，与直线y2=-x-3交点为A和C．(1)求抛物线的解析式；(2)在直线y2=-x-3上是否存在一点M，使得△ABM是等腰直角三角形，如果存在，求出点M的坐标，如果不存在请说明理由．(3)若点E是x轴上一个动点，把点E向下平移4个单位长度得到点F，点F向右平移4个单位长度得到点G，点G向上平移4个单位长度得到点H，若四边形EFGH与抛物线有公共点，请直接写出点E的横坐标x E的取值范围．【题型4二次函数中全等三角形的存在性问题】1(2023·陕西咸阳·统考三模)如图，抛物线y=14x2-2x+3与x轴交于A、B两点，抛物线的顶点为C，对称轴为直线l，l交x轴于点D．(1)求点A、B、C的坐标；(2)点P是抛物线上的动点，过点P作PM⊥y轴于点M，点N在y轴上，且点N在点M上方，是否存在这样的点P、N，使得以点P、M、N为顶点的三角形与△BCD全等，若存在，请求出点P、N的坐标；若不存在，请说明理由．1(2023·甘肃陇南·统考一模)如图，抛物线y=x2+bx+c与x轴交于A-1,0，B两点，与y轴交于点C0,-3．(1)求抛物线的函数解析式；(2)已知点P m,n在抛物线上，当-1≤m<3时，直接写出n的取值范围；(3)抛物线的对称轴与x轴交于点M，点D坐标为2,3，试问在该抛物线上是否存在点P，使△ABP与△ABD全等？若存在，请求出所有满足条件的P点的坐标；若不存在，请说明理由．2(2023·陕西咸阳·统考三模)如图，抛物线y=14x2-2x+3与x轴交于A，B两点，抛物线的顶点为C，对称轴为直线l，l交x轴于点D．(1)求点A、B、C的坐标；(2)点P是抛物线上的动点，过点P作PM⊥y轴于点M，点N在y轴上，且点N在点M上方，是否存在这样的点P、N，使得以点P、M、N为顶点的三角形与△BCD全等，若存在，请求出点P、N的坐标；若不存在，请说明理由．3(2023·内蒙古通辽·统考中考真题)如图，在平面直角坐标系中，抛物线y=ax2+bx+c(a≠0)的顶点为B(2，1)，且过点A(0，2)，直线y=x与抛物线交于点D，E(点E在对称轴的右侧)，抛物线的对称轴交直线y=x于点C，交x轴于点G，EF⊥x轴，垂足为F，点P在抛物线上，且位于对称轴的右侧，PQ⊥x轴，垂足为点Q，△PCQ为等边三角形(1)求该抛物线的解析式；(2)求点P的坐标；(3)求证：CE=EF；(4)连接PE，在x轴上点Q的右侧是否存在一点M，使△CQM与△CPE全等？若存在，试求出点M的坐标；若不存在，请说明理由．[注：3+22=(2+1)2]．【题型5二次函数中平行四边形的存在性问题】1(2023春·云南临沧·九年级统考期末)如图，抛物线y=ax2+bx-3与x轴交于A-1,0两点，、B3,0与y轴交于点C．(1)求抛物线的解析式；(2)若点D是抛物线上的一点，当△ABD的面积为10时，求点D的坐标；(3)点P是抛物线对称轴上的一点，在抛物线上是否存在一点Q，使得以B、C、P、Q为顶点的四边形是平行四边形？若存在，求出点Q的坐标；若不存在，请说明理由．1(2023春·山东东营·九年级校考期末)如图，已知抛物线y=ax2+bx+3与x轴交于A-1,0、B3,0两点，与y轴交于点C，连接BC．(1)求抛物线的解析式；(2)若点P为线段BC上的一动点(不与B、C重合)，PM∥y轴，且PM交抛物线于点M，交x轴于点N，当△BCM的面积最大时，求点P的坐标；(3)在(2)的条件下，当△BCM的面积最大时，点D是抛物线的对称轴上的动点，在抛物线上是否存在点E，使得以A、P、D、E为顶点的四边形为平行四边形？若存在，请直接写出点E的坐标；若不存在，请说明理由．2(2023春·重庆梁平·九年级统考期末)如图1，在平面直角坐标系中，抛物线y=-2x2+4x+6与y轴交于点A，与x轴交于点E，B(E在B的左侧)．(1)如图2，抛物线的顶点为点Q，求△BEQ的面积；(2)如图3，过点A作AC平行于x轴，交抛物线于点C，点P为抛物线上的一点(点P在AC上方)，作PD 平行于y轴交AB于点D、交AC于点F，当点P在何位置时，PD+CF最大？求出最大值；(3)在(2)条件下，当PD+CF最大时，将抛物线y=-2x2+4x+6沿着射线AB平移，使得抛物线经过点C，此时得到新抛物y ，点N是原抛物线对称轴上一点，在新抛物线y 上是否存在一点M，使以点A，D，M，N为顶点的四边形为平行四边形，若存在，请直接写出点M的所有坐标，若不存在，请说明理由．3(2023春·重庆江北·九年级重庆十八中校考期末)如图1，抛物线y=ax2+bx+3a≠0与x轴正半轴交于点A，B，与y轴正半轴交于点C，且OC=OB=3OA，点D为抛物线的顶点．(1)求该抛物线的函数表达式；(2)点P为直线BC下方该抛物线上任意一点，点E为直线BC与该抛物线对称轴的交点，求△PBE面积的最大值；(3)如图2，将该抛物线沿射线CB的方向平移22个单位后得到新抛物线y ，新抛物线y 的顶点为D ，过(2)问中使得△PBE面积为最大时的点P作平行于y轴的直线交新抛物线y 于点M．在新抛物线y 的对称轴上是否存在点N，使得以点P，D ，M，N为顶点的四边形是平行四边形？若存在，请直接写出点N的坐标；若不存在，请说明理由．【题型6二次函数中菱形的存在性问题】1(2023春·重庆云阳·九年级校联考期中)如图1，抛物线y=ax2+bx+c(a≠0)与x轴相交于点A、B(点B在点A左侧)，与y轴相交于点C(0,3)．已知点A坐标为(1,0)，△ABC面积为6．(1)求抛物线的解析式；(2)点P是直线BC上方抛物线上一动点，过点P作直线BC的垂线，垂足为点E，过点P作PF∥y轴交BC于点F，求△PEF周长的最大值及此时点P的坐标：(3)如图2，将该抛物线向左平移2个单位长度得到新的抛物线y ，平移后的抛物线与原抛物线相交于点D，点M为直线BC上的一点，点N是平面坐标系内一点，是否存在点M，N，使以点B，D，M，N为顶点的四边形为菱形，若存在，请直接写出点M的坐标；若不存在，请说明理由．1(2023春·甘肃庆阳·九年级统考期末)如图，在平面直角坐标系中，二次函数y=x2+bx+c的图象与x轴交于A、B两点，与y轴交于点C0,-3，点P是直线BC下，点A在原点的左侧，点B的坐标为3,0方的抛物线上一动点．(1)求这个二次函数的表达式．(2)连接PO、PC，并把△POC沿CO所在直线翻折，得到四边形POP C，那么是否存在点P，使四边形POP C为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．(3)当点P运动到什么位置时，四边形ABPC的面积最大？求出此时P点的坐标和四边形ABPC的面积．点，抛物线y=-x2+bx+c经过点B，且与x轴交于点C(2,0)．(1)求该抛物线的解析式；(2)已知点M是抛物线上的一个动点，并且点M在第一象限内，连接AM、BM，设点M的横坐标为m，四边形OAMB的面积为S，求S与m的函数表达式，并求出S的最大值；(3)若点P在平面内，点Q在直线AB上，平面内是否存在点P使得以O，B，P，Q为顶点的四边形是菱形．若存在，求出点P的坐标；若不存在，请说明理由．点，抛物线y=-x2+bx+c经过点B，且与x轴交于点C(2,0)．(1)求该抛物线的解析式；(2)已知点M是抛物线上的一个动点，并且点M在第一象限内，连接AM、BM，设点M的横坐标为m，四边形OAMB的面积为S，求S与m的函数表达式，并求出S的最大值；(3)若点P在平面内，点Q在直线AB上，平面内是否存在点P使得以O，B，P，Q为顶点的四边形是菱形．若存在，求出点P的坐标；若不存在，请说明理由．【题型7二次函数中矩形的存在性问题】1(2023春·浙江湖州·九年级统考期末)如图，在平面直角坐标系xOy中，O为坐标原点，抛物线y=a(x+3)(x-1)(a>0)与x轴交于A，B两点(点A在点B的左侧)．(1)求点A与点B的坐标；(2)若a=13，点M是抛物线上一动点，若满足∠MAO不大于45°，求点M的横坐标m的取值范围．(3)经过点B的直线l：y=kx+b与y轴正半轴交于点C．与抛物线的另一个交点为点D，且CD=4BC．若点P在抛物线对称轴上，点Q在抛物线上，以点B，D，P，Q为顶点的四边形能否成为矩形？若能，求出点P的坐标；若不能，请说明理由．1(2023·山东东营·东营市胜利第一初级中学校考三模)已知抛物线y=ax2+bx-4a≠0交x轴于点A4,0和点B-2,0，交y轴于点C．(1)求抛物线的解析式；(2)如图，点P是抛物线上位于直线AC下方的动点，过点P分别作x轴、y轴的平行线，交直线AC于点D，交x轴于点E，当PD+PE取最大值时，求点P的坐标及PD+PE最大值．(3)在抛物线上是否存在点M，对于平面内任意点N，使得以A、C、M、N为顶点且AC为一条边的四边形为矩形，若存在，请直接写出M、N的坐标，不存在，请说明理由．2(2023春·内蒙古通辽·九年级校考期中)如图，抛物线y=ax2+bx+3交x轴于A(3,0),B(-1,0)两点，交y轴于点C．(1)求抛物线的解析式和对称轴．SΔABC，求R的坐标．(2)若R为第一象限内抛物线上点，满足SΔRAC=12(3)若点P在抛物线的对称轴上，点Q是平面直角坐标系内的任意一点，是否存在点P使得A、C、P、Q为顶点的四边形是矩形，若存在，请直接写出所有符合条件的点P的坐标．3(2023春·广东江门·九年级校考期末)如图，在平面直角坐标系中，已知抛物线y=ax2+bx-2a≠0、B两点，交y轴于点C，其对称轴为x=1.5，交x轴于A-1，0(1)求该抛物线的函数解析式；(2)P为第四象限内抛物线上一点，连接PB，过点C作CQ∥BP交x轴于点Q，连接PQ，求△PBQ面积的最大值及此时点P的坐标．(3)在(2)的条件下，将抛物线y=ax2+bx-2a≠0向右平移经过点Q，得到新抛物线，点E在新抛物线的对称轴上，是否在平面内存在一点F，使得以A、P、E、F为顶点的四边形是矩形？若存在，直接写出点F的坐标；若不存在，请说明理由．【题型8二次函数中正方形的存在性问题】1(2023·辽宁阜新·阜新实验中学校考一模)如图，在平面直角坐标系中，抛物线y=ax2+bx-3与x轴交于A(-1,0)，B(3,0)两点，与y轴交于点C，点P为抛物线上的动点．(1)求该抛物线的函数表达式；(2)点D为直线y=x上的动点，当点P在第四象限时，求四边形PBDC面积的最大值及此时点P的坐标；(3)已知点E为x轴上一动点，点Q为平面内任意一点，是否存在以点P，C，E，Q为顶点的四边形是以PC为对角线的正方形，若存在，请直接写出点Q的坐标，若不存在，请说明理由．1(2023·陕西西安·校考模拟预测)如图，已知拋物线y=-x2+2x+c与x轴交于点A3,0，B与y轴交于点C．(1)求c的值及该抛物线的对称轴；(2)若点D在直线AC上，点E是平面内一点．是否存在点E，使得以点A,B,D,E为顶点的四边形为正方形？若存在，请求出点E的坐标；若不存在，请说明理由．2(2023·山西晋中·山西省平遥中学校校考模拟预测)如图，二次函数y=-x2+2x+3的图象与x轴交于A，B两点(点A在点B左侧)，与y轴交于点C．连接BC．点P是抛物线第一象限内的一个动点，设点P的横坐标为m，过点P作直线PD⊥x轴于点D．交BC于点E．过点P作BC的平行线，交y轴于点M．(1)求A，B，C三点的坐标，并直接写出直线BC的函数表达式；(2)在点P的运动过程中，求使四边形CEPM为菱形时，m的值；(3)点N为平面内任意一点，在(2)的条件下，直线PM上是否存在点Q使得以P，E，Q，N为顶点的四边形是正方形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．3(2023·江西赣州·统考一模)已知二次函数C1：y=mx2-2mx+3(m≠0)．(1)有关二次函数C1的图象与性质，下列结论中正确的有．(填序号)①二次函数C1的图象开口向上；②二次函数C1的图象的对称轴是直线x=1；③二次函数C1的图象经过定点(0，3)和(2，3)；④函数值y随着x的增大而减小．(2)当m=1时，①抛物线C1的顶点坐标为；②将抛物线C1沿x轴翻折得到抛物线C2，则抛物线C2的表达式为；(3)设抛物线C1与y轴相交于点E，过点E作直线l∥x轴，与抛物线C1的另一交点为F，将抛物线C1沿直线l翻折，得到抛物线C3，抛物线C1，C3的顶点分别记为P，Q．是否存在实数m，使得以点E，F，P，Q为顶点的四边形为正方形？若存在，请求出m的值；若不存在，请说明理由．【题型9二次函数中面积问题的存在性问题】1(2023春·四川广安·九年级统考期末)如图1，抛物线y=ax2+bx+3经过A1,0两点，交y轴于,B3,0点C．(1)求抛物线的函数解析式．(2)在抛物线的对称轴上是否存在一点M，使得△ACM的周长最小？若存在，求出点M的坐标；若不存在，请说明理由．S△BCA，请直接写出点P的横坐(3)如图2，连接BC，若在BC下方的抛物线上存在一点P，使得S△BCP=12标．1(2023春·江西九江·九年级校考期中)如图，已知二次函数L1：y=x2+bx+c与x轴交于A、B两点，A点坐标(-1，0)，B点坐标(3,0)，与y轴交于点C，直线L2：y=x+n经过点A．(1)求二次函数L1的表达式及顶点P的坐标；(2)二次函数L3与二次函数L1关于X轴对称，直线L2与二次函数L3相交于A、D两点．①直接写出二次函数L3的表达式；②求出D点的坐标；③在直线L2上半部分的二次函数L3上，是否存在一点M，使得△AMD的面积最大？若存在，请求出M坐标，并求出最大面积．2(2023春·山东东营·九年级东营市实验中学校考期中)如图，抛物线y=ax2+bx+c a≠0与y轴交于点C0,4．，点B4,0，与x轴交于A-2,0(1)求抛物线的解析式；(2)若点M是抛物线上的一动点，且在直线BC的上方，当S△MBC取得最大值时，求点M的坐标；(3)在抛物线上是否存在点P，使三角形ABP的面积为12？若存在，直接写出点P的坐标；若不存在，请说明理由．3(2023春·福建泉州·九年级统考期末)如图，在平面直角坐标系xOy中，顶点为E1，4的抛物线y= ax2+bx+c与x轴从左到右依次交于A，B两点，与y轴的交点为C0，3，P是抛物线对称轴右侧图象上的一点，且在x轴的上方．(1)求此抛物线的解析式；(2)若直线BP与抛物线对称轴交于点D，当BD-CD取得最大值时，求点P的坐标；(3)若直线BC与抛物线对称轴交于点F，连接PC，PE，PF，记△PCF，△PEF的面积分别为S1，S2，判断2S1+S2是否存在最大值．若存在，求出最大值；若不存在，请说明理由．【题型10二次函数中线段问题的存在性问题】1(2023春·内蒙古巴彦淖尔·九年级校考期中)如图1，抛物线y=ax2+bx+c a≠0与x轴交于A-8,0．点E是第二象限内抛物线上的一个动点，设点E的横坐标 两点，与y轴交于点D0,4，C2,0为n，过点E作直线EB⊥x轴于点B，作直线AD交EB于点F．(1)求该抛物线的解析式；(2)如图1，当△EFD是以FD为底边的等腰三角形时，求点E的坐标；(3)如图2，连接CD，过点E作直线l∥CD，交y轴于点H，连接BH．试探究：在点E运动的过程中，是否存在点E，使得FD=BH，若存在，请求出点E的坐标；若不存在，请说明理由．1(2023春·四川南充·九年级统考期中)如图，平面直角坐标系中的Rt△AOB和Rt△COD全等，直角边OB、OD在x轴上．已知点C的坐标为4，2，过A、C两点的直线分别交x轴、y轴于点E、F，抛物线y=ax2+bx+c经过O、A、C三点．(1)写出点A的坐标并求该抛物线的函数解析式；(2)点G为抛物线上位于线段OC所在可直线上方部分的一动点，求G到直线OC的最大距离和此时点G 的坐标；(3)点P为线段OC上一个动点，过点P作y轴的平行线交抛物线于点M，交x轴于点N，问是否存在这样的点P，使得四边形ABPM的边AM与边BP相等？若存在，求出此时点P的坐标；若不存在，请说明理由．2(2023春·云南曲靖·九年级统考期末)已知抛物线y=x2+bx+c与x轴交于点A-1,0两，B3,0点，与y轴交于点C，连接BC．(1)求抛物线的解析式；(2)在抛物线上是否存在点M，使得B、C两点到直线AM的距离相等，如果存在，求出点M的坐标，如果不存在，请说明理由；(3)点P为x轴上一动点，以P为旋转中心，把线段BC逆时针旋转90°，得到线段GH，其中点B的对应点为点G，当抛物线的对称轴刚好经过GH中点时，求此时点P的坐标．3(2023春·安徽阜阳·九年级校考期末)如图，已知抛物线经过原点O和x轴上另一点A，它的对称轴x=-2与x轴交于点C，直线y=-2x+1经过抛物线上一点B2,m，且与y轴．直线x=-2分别交于点D、E．(1)求m的值及该抛物线对应的函数关系式；(2)①判断△CBE的形状，并说明理由；②判断CD与BE的位置关系；(3)若P x,y是该抛物线上的一个动点，是否存在这样的点P，使得PB=PE？若存在，试求出所有符合条件的点P的坐标；若不存在，请说明理由．【题型11二次函数中角度问题的存在性问题】1(2023春·辽宁葫芦岛·九年级统考期末)如图，在平面直角坐标系中，已知抛物线y=-x2+bx+c与x轴交于A，B4,0在抛物线上，点P是抛物线上一动点．两点，与y轴交于点C，点D3,4(1)求该抛物线的解析式；(2)如图1，连接OD，若OP平分∠COD，求点P的坐标；(3)如图2，连接AC，BC，抛物线上是否存在点P，使∠CBP+∠ACO=45°？若存在，请直接写出点P的坐标；若不存在，请说明理由．1(2023春·内蒙古鄂尔多斯·九年级统考期末)如图，直线y=-x+3与x轴、y轴分别交于B、C两点，抛物线y=-x2+bx+c经过点B、C，与x轴另一交点为A，顶点为D．(1)求抛物线的解析式；(2)在第四象限的抛物线上是否存在一点M，使△MBC的面积为27？若存在，求出M点坐标；若不存在，请说明理由．(3)在抛物线的对称轴上是否存在一点P，使得∠APB=∠OCB？若存在，求出P点坐标；若不存在，请说明理由．2(2023春·江苏盐城·九年级统考期末)如图，抛物线y=12x2+mx+n与x轴交于A，B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知A-4,0,C0,-2．(1)求抛物线的函数表达式；(2)点E是线段AC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDAF的面积最大?求出四边形CDAF的最大面积及此时E点的坐标；(3)在y轴上是否存在点P，使得∠OAP+∠OAC=60°？若存在，请直接写出P点的坐标，若不存在，请说明理由．3(2023春·浙江湖州·九年级统考期末)如图，在平面直角坐标系中，直线y=12x-2与x轴交于点A，与y轴交于点C，抛物线y=12x2+bx+c经过A，C两点，与x轴的另一交点为点B，点P为抛物线上的一个动点．(1)求抛物线的函数表达式；(2)当△ACP的面积与△ABC的面积相等时，求点P的坐标；(3)是否存在点P，使得∠ACP=∠ABC-∠BAC，若存在，请直接写出点P的横坐标；若不存在，请说明理由．【题型12二次函数中最值问题的存在性问题】1(2023春·甘肃庆阳·九年级统考期中)如图，已知抛物线y=38x2-34x-3与x轴的交点为点A、D(点A在点D的右侧)，与y轴的交点为点C．(1)直接写出A、D、C三点的坐标；(2)在抛物线的对称轴上找一点M，使得MD+MC的值最小，并求出点M的坐标；(3)设点C关于抛物线对称轴的对称点为点B，在抛物线上是否存在点P，使得以A、B、C、P四点为顶点的四边形为梯形？若存在，求出点P的坐标；若不存在，请说明理由．1(2023春·浙江宁波·九年级校考期中)对于给定的两个函数，任取自变量x 的一个值，当x <0时，它们对应的函数值互为相反数；当x ≥0时，它们对应的函数值相等，我们称这样的两个函数互为“伴随”函数．例如：一次函数y =x -3，它的“伴随”函数为y =-x +3x <0 x -3x ≥0 ．(1)已知点M -2，1 在一次函数y =-mx +1的“伴随”函数的图象上，求m 的值．(2)已知二次函数y =-x 2+4x -12．①当点A a ，32 在这个函数的“伴随”函数的图象上时，求a 的值．②当-3≤x ≤3时，函数y =-x 2+4x -12的“伴随”函数是否存在最大值或最小值，若存在，请求出最大值或最小值；若不存在，请说明理由．。

二次函数与直角三角形有关的问题知识解读【专题说明】二次函数之直角三角形存在性问题，主要指的是在平面直角坐标系下，已知一条边（或两个顶点）的直角三角形存在，求第三个顶点的坐标的题型.主要考察学生对转化思想、方程思想、几何问题代数化的数形结合思想及分类讨论思想的灵活运用。

【解题思路】直角三角形的存在性问题1.找点：在已知两定点，确定第三点构成直角三角形时，要么以两定点为直角顶点，要么以动点为直角顶点.以定点为直角顶点时，构造两条直线与已知直线垂直;以动点为直角顶点时，以已知线段为直径构造圆找点2.方法：（1）以两定点为直角顶点时，两直线互相垂直，则k1*k2=-1（2）以已知线段为斜边时，利用K型图，构造双垂直模型，最后利用相似求解，或者三条边分别表示之后，利用勾股定理求解下面主要介绍2种常用方法：【方法1 几何法】“两线一圆”（1）若∠A 为直角，过点A 作AB 的垂线，与x 轴的交点即为所求点C；（2）若∠B 为直角，过点B 作AB 的垂线，与x 轴的交点即为所求点C；（3）若∠C 为直角，以AB 为直径作圆，与x 轴的交点即为所求点C．（直径所对的圆周角为直角）如何求得点坐标？以C2为例：构造三垂直．），坐标为（故代入得：坐标得、由，易证0213232222C C C BN AM B A N MB BN AM BN AMB ===∆≈∆()），坐标为（，，坐标为故或故又即代入得：设，，坐标得、由求法相同，如下：易证、040231a ,4a ,3ab ,3ab 1N a,31,4333333343C C C C C C C C C C b b M BN AM B A NBM N AMNB AM ==+=======∆≈∆【方法2 代数法】点-线-方程23m 20352235110,m 135-m 1-m 35-m 11-m 22222122111=+=+=+=+==，解得：）代入得方程（，，，）表示线段：（）；，（）、，（），又坐标为（）表示点：设（：不妨来求下）（）（）（）（BC C C C A AB B A【典例分析】【方法1 勾股定理】【典例1】（2021秋•建华区期末）抛物线y＝x2+bx+c经过A、B（1，0）、C（0，﹣3）三点．点D为抛物线的顶点，连接AD、AC、BC、DC．（1）求抛物线的解析式；（2）在y轴上是否存在一点E，使△ADE为直角三角形？若存在，请你直接写出点E的坐标；若不存在，请说明理由．【解答】解（1）∵抛物线y＝x2+bx+c经过B（1，0）、C（0，﹣3），∴，解得，∴抛物线的解析式为：y＝x2+2x﹣3．（4）在y轴上存在点E，使△ADE为直角三角形，理由如下：∵抛物线的解析式为y＝x2+2x﹣3＝（x+1）2﹣4，∴D（﹣1，﹣4），设E点坐标为（0，m），∴AE2＝m2+9，DE2＝m2+8m+17，AD2＝20，当∠EAD＝90°时，有AE2+AD2＝DE2，∴m2+9+20＝m2+8m+17，解得m＝，∴此时点E的坐标为（0，）；当∠ADE＝90°时，DE2+AD2＝AE2，m2+8m+17+20＝m2+9，解得m＝﹣，∴此时点E的坐标为（0，﹣）；当∠AED＝90°时，AE2+DE2＝AD2，m2+9+m2+8m+17＝20，解得m＝﹣1或m＝﹣3，∴此时点E的坐标为（0，﹣1）或（0，﹣3）．【变式1-1】（2022•灞桥区校级模拟）如图，抛物线与x轴交于点A（1，0），B（3，0），与y轴交于点C（0，3）．（1）求二次函数的表达式及顶点坐标；（2）连接BC，在抛物线的对称轴上是否存在一点E，使△BCE是直角三角形？若存在，请直接写出点E的坐标；若不存在，请说明理由．【解答】解：（1）设抛物线的解析式为y＝a（x﹣1）（x﹣3），将点C（0，3）代入y＝a（x﹣1）（x﹣3），∴3a＝3，∴a＝1，∴y＝（x﹣1）（x﹣3）＝x2﹣4x+3，∵y＝x2﹣4x+3＝（x﹣2）2﹣1，∴顶点为（2，﹣1）；（2）存在一点E，使△BCE是直角三角形，理由如下：∵y＝x2﹣4x+3＝（x﹣2）2﹣1，∴抛物线的对称轴为直线x＝2，设E（2，t），∵△BCE是直角三角形，∴BE⊥CE，∵B（3，0），C（0，3），∴BC＝3，BE＝，CE＝，①当BC为斜边时，∴18＝（）2+（）2，解得t＝，∴E点坐标为（2，）或（2，）；②当BE为斜边时，∴18+（）2＝（）2，解得t＝5，∴E点坐标为（2，5）；③当CE为斜边时，∴18+（）2＝（）2，解得t＝﹣1，∴E点坐标为（2，﹣1）；综上所述：E点坐标为（2，）或（2，）或（2，5）或（2，﹣1）【变式1-2】（2022•广安）如图，在平面直角坐标系中，抛物线y＝ax2+x+m（a≠0）的图象与x轴交于A、C两点，与y轴交于点B，其中点B坐标为（0，﹣4），点C坐标为（2，0）．（1）求此抛物线的函数解析式．（2）点P为该抛物线对称轴上的动点，使得△P AB为直角三角形，请求出点P的坐标．【解答】解：（1）∵抛物线y＝ax2+x+m（a≠0）的图象经过点B（0，﹣4），点C（2，0），∴，解得，∴抛物线的解析式为y＝x2+x﹣4；（2）如图2中，设抛物线的对称轴交x轴于点N，过点B作BM⊥抛物线的对称轴于点M．则N（﹣1.0）．M（﹣1，﹣4）；∵OA＝OB＝4，∠AOB＝90°，∴∠OAB＝∠OBA＝45°，当∠P1AB＝90°时，△ANP1是等腰直角三角形，∴AN＝NP1＝3，∴P1（﹣1，3），当∠ABP2＝90°时，△BMP2是等腰直角三角形，可得P2（﹣1，﹣5），当∠APB＝90°时，设P（﹣1，n），设AB的中点为J，连接PJ，则J（﹣2，﹣2），∴PJ＝AB＝2，∴12+（n+2）2＝（2）2，解得n＝﹣2或﹣﹣2，∴P3（﹣1，﹣2），P4（﹣1，﹣﹣2），综上所述，满足条件的点P的坐标为（﹣1，3）或（﹣1，﹣5）或（﹣1，﹣2）或（﹣1，﹣﹣2）．【方法2 构造“K”字型利用相似作答】【典例2】（2022•碑林区校级四模）如图，在平面直角坐标系中，抛物线C1：y＝ax2+bx+c 交x轴于点A（﹣5，0），B（﹣1，0），交y轴于点C（0，5）．（1）求抛物线C1的表达式和顶点D的坐标．（2）将抛物线C1关于y轴对称的抛物线记作C2，点E为抛物线C2上一点若△DOE是以DO为直角边的直角三角形，求点E的坐标．【解答】解：（1）将点A（﹣5，0），B（﹣1，0），C（0，5）代入y＝ax2+bx+c，∴，解得，∴y＝x2+6x+5，∵y＝x2+6x+5＝（x+3）2﹣4，∴顶点D（﹣3，﹣4）；（2）设抛物线C2上任意一点（x，y），则（x，y）关于y轴对称的点为（﹣x，y），∵点（﹣x，y）在抛物线C1上，∴抛物线记作C2的解析式为y＝x2﹣6x+5，设E（t，t2﹣6t+5），过点D作DG⊥x轴交于点G，过点E作EH⊥x轴交于点H，∵∠DOE＝90°，∴∠GOD+∠HOE＝90°，∵∠GOD+∠GDO＝90°，∴∠HOE＝∠GDO，∴△GDO∽△HOE，∴＝，∵DG＝4，GO＝3，HE＝﹣t2+6t﹣5，OH＝t，∴＝，∴t＝4或t＝，∴E（4，﹣3）或E（，﹣）．【变式2-1】（2022•济南）抛物线y＝ax2+x﹣6与x轴交于A（t，0），B（8，0）两点，与y轴交于点C，直线y＝kx﹣6经过点B．点P在抛物线上，设点P的横坐标为m．（1）求抛物线的表达式和t，k的值；（2）如图1，连接AC，AP，PC，若△APC是以CP为斜边的直角三角形，求点P的坐标；【解答】解：（1）将B（8，0）代入y＝ax2+x﹣6，∴64a+22﹣6＝0，∴a＝﹣，∴y＝﹣x2+x﹣6，当y＝0时，﹣t2+t﹣6＝0，解得t＝3或t＝8（舍），∴t＝3，∵B（8，0）在直线y＝kx﹣6上，∴8k﹣6＝0，解得k＝，∴y＝x﹣6；（2）作PM⊥x轴交于M，∵P点横坐标为m，∴P（m，﹣m2+m﹣6），∴PM＝m2﹣m+6，AM＝m﹣3，在Rt△COA和Rt△AMP中，∵∠OAC+∠P AM＝90°，∠APM+∠P AM＝90°，∴∠OAC＝∠APM，∴△COA∽△AMP，∴＝，即OA•MA＝CO•PM，3（m﹣3）＝6（m2﹣m+6），解得m＝3（舍）或m＝10，∴P（10，﹣）；【变式2-2】（2022•滨州）如图，在平面直角坐标系中，抛物线y＝x2﹣2x﹣3与x轴相交于点A、B（点A在点B的左侧），与y轴相交于点C，连接AC、BC．（1）求线段AC的长；（2）若点M为该抛物线上的一个动点，当△BCM为直角三角形时，求点M的坐标．【解答】解：（1）针对于抛物线y＝x2﹣2x﹣3，令x＝0，则y＝﹣3，∴C（0，﹣3）；令y＝0，则x2﹣2x﹣3＝0，∴x＝3或x＝﹣1，∵点A在点B的左侧，∴A（﹣1，0），B（3，0），∴AC＝＝；（2）由（1）知，B（3，0），C（0，﹣3），∴OB＝OC＝3，设M（m，m2﹣2m﹣3），∵△BCM为直角三角形，∴①当∠BCM＝90°时，如图1，过点M作MH⊥y轴于H，则HM＝m，∵OB＝OC，∴∠OCB＝∠OBC＝45°，∴∠HCM＝90°﹣∠OCB＝45°，∴∠HMC＝45°＝∠HCM，∴CH＝MH，∵CH＝﹣3﹣（m2﹣2m﹣3）＝﹣m2+2m，∴﹣m2+2m＝m，∴m＝0（不符合题意，舍去）或m＝1，∴M（1，﹣4）；②当∠CBM＝90°时，过点M作M'H'⊥x轴，同①的方法得，M'（﹣2，5）；③当∠BMC＝90°时，如图2，Ⅰ、当点M在第四象限时，过点M作MD⊥y轴于D，过点B作BE⊥DM，交DM的延长线于E，∴∠CDM＝∠E＝90°，∴∠DCM+∠DMC＝90°，∵∠DMC+∠EMB＝90°，∴∠DCM＝∠EMB，∴△CDM∽△MEB，∴，∵M（m，m2﹣2m﹣3），B（3，0），C（0，﹣3），∴DM＝m，CD＝﹣3﹣（m2﹣2m﹣3）＝﹣m2+2m，ME＝3﹣m，BE＝﹣（m2﹣2m﹣3）＝﹣m2+2m+3，∴，∴m＝0（舍去）或m＝3（点B的横坐标，不符合题意，舍去）或m＝（不符合题意，舍去）或m＝，∴M（，﹣），Ⅱ、当点M在第三象限时，M（，﹣），即满足条件的M的坐标为（1，﹣4）或（﹣2，5）或（，﹣），或（，﹣）．。

中考数学专题复习：二次函数综合题（特殊三角形问题）1．如图，已知抛物线经过点A (-1，0)，B (4，0)，C (0，2)三点，点D 与点C 关于x 轴对称，点P 是线段AB 上的一个动点，设点P 的坐标为(m ，0)，过点P 作x 轴的垂线l 交抛物线于点Q ，交直线BD 于点M ．(1)求该抛物线所表示的二次函数的表达式；(2)在点P 运动过程中，是否存在点Q ，使得△BQM 是直角三角形？若存在，求出点Q 的坐标；若不存在，请说明理由；(3)连接AC ，将△AOC 绕平面内某点H 顺时针旋转90°，得到111A O C △，点A 、O 、C 的对应点分别是点1A 、1O 、1C 、若111A O C △的两个顶点恰好落在抛物线上，那么我们就称这样的点为“和谐点”，请直接写出“和谐点”的个数和点1A 的横坐标．2．如图，已知A （﹣2，0）、B （3，0），抛物线y ＝ax 2＋bx ＋4经过A 、B 两点，交y 轴于点C ．点P 是第一象限内抛物线上的一动点，点P 的横坐标为m ．过点P 作PM ⊥x 轴，垂足为点M ，PM 交BC 于点Q ．过点P 作PN ⊥BC ，垂足为点N ．(1)直接写出抛物线的函数关系式 ；(2)请用含m 的代数式表示线段PN 的长 ；(3)连接PC ，在第一象限的抛物线上是否存在点P ，使得⊥BCO ＋2⊥PCN ＝90°？若存在，请求出m 的值；若不存在，请说明理由；(4)连接AQ ，若△ACQ 为等腰三角形，请直接写出m 的值 ．3．如图，抛物线2y ax bx =+过()4,0A ，()1,3B 两点，点C 、B 关于抛物线的对称轴对称，过点B 作直线BH x ⊥轴，交x 轴于点H ．(1)求抛物线的表达式；(2)求ABC 的面积；(3)若点M 在直线BH 上运动，点N 在x 轴上运动，当CMN △为等腰直角三角形时，点N 的坐标为______．4．如图，已知二次函数的图象经过点()3,3A 、()4,0B 和原点O ．P 为二次函数图象上的一个动点，过点P 作x 轴的垂线，垂足为(),0D m ，并与直线OA 交于点C ．(1)求出二次函数的解析式；(2)当点P 在直线OA 的上方时，求线段PC 的最大值；(3)当0m >时，探索是否存在点P ，使得PCO △为等腰三角形，如果存在，求出P 的坐标；如果不存在，请说明理由．5．如图，在平面直角坐标系中，抛物线2y ax x m =++（a ≠0）的图象与x 轴交于A 、C 两点，与y 轴交于点B ，其中点B 坐标为（0，－4），点C 坐标为（2，0）．(1)求此抛物线的函数解析式．(2)点D 是直线AB 下方抛物线上一个动点，连接AD 、BD ，探究是否存在点D ，使得⊥ABD 的面积最大？若存在，请求出点D 的坐标；若不存在，请说明理由．(3)点P 为该抛物线对称轴上的动点，使得⊥P AB 为直角三角形，请求出点P 的坐标．6．如图，在平面直角坐标系xOy 中，抛物线26y ax bx =++与x 轴交于点()2,0A -和点()6,0B ，与y 轴交于点C ，顶点为D ，连接BC 交抛物线的对称轴l 于点E ．(1)求抛物线的表达式；(2)连接CD 、BD ，点P 是射线DE 上的一点，如果PDB CDB S S =△△，求点P 的坐标；(3)点M 是线段BE 上的一点，点N 是对称轴l 右侧抛物线上的一点，如果EMN 是以EM 为腰的等腰直角三角形，求点M 的坐标．7．已知抛物线经过A （－1，0）、B （0、3）、 C （3，0）三点，O 为坐标原点，抛物线交正方形OBDC 的边BD 于点E ，点M 为射线BD 上一动点，连接OM ，交BC 于点F(1)求抛物线的表达式；(2)求证：⊥BOF ＝⊥BDF ：(3)是否存在点M 使⊥MDF 为等腰三角形？若不存在，请说明理由；若存在，求ME 的长8．如图，抛物线23y ax x c =-+与x 轴交于(4,0)A -，B 两点，与y 轴交于点(0,4)C ，点D 为x 轴上方抛物线上的动点，射线OD 交直线AC 于点E ，将射线OD 绕点O 逆时针旋转45︒得到射线OP ，OP 交直线AC 于点F ，连接DF ．(1)求抛物线的解析式；(2)当点D 在第二象限且34DE EO =时，求点D 的坐标； (3)当ODF △为直角三角形时，请直接写出点D 的坐标．9．已知二次函数214y x bx c =-++图像的对称轴与x 轴交于点A （1，0），图像与y 轴交于点B （0，3），C 、D 为该二次函数图像上的两个动点（点C 在点D 的左侧），且90CAD ∠=．(1)求该二次函数的表达式；(2)若点C 与点B 重合，求tan⊥CDA 的值；(3)点C 是否存在其他的位置，使得tan⊥CDA 的值与（2）中所求的值相等？若存在，请求出点C 的坐标；若不存在，请说明理由．10．如图1，抛物线y =-x 2+bx +c 交x 轴于A ，B 两点，交y 轴于C 点，D 是抛物线上的动点，已知A 的坐标为（-3，0），C 的坐标为（0，3）．(1)求该抛物线的函数表达式以及B 点的坐标；(2)在第二象限内是否存在点D 使得⊥ACD 是直角三角形且⊥ADC=90°，若存在请求出D 点的坐标，若不存在请说明理由；(3)如图2，连接AC ，BC ，当⊥ACD=⊥BCO ，求D 点的坐标．11．如图，在平面直角坐标系中，抛物线C 1：y ＝ax 2＋bx ﹣1经过点A (﹣1,﹣2)和点B (﹣2,1)，抛物线C 2：y ＝3x 2＋3x ＋1，动直线x ＝t 与抛物线C 1交于点N ，与抛物线C 2交于点M ．(1)求抛物线C 1的表达式；(2)求线段MN 的长（用含t 的代数式表达）；(3)当⊥BMN 是以MN 为直角边的等腰直角三角形时，求t 的值．12．如图，二次函数23y ax bx =++的图象经过点A （-1，0），B （3，0），与y 轴交于点C ．(1)求二次函数的解析式；(2)第一象限内的二次函数23y ax bx =++图象上有一动点P ，x 轴正半轴上有一点D ，且OD =2，当S △PCD =3时，求出点P 的坐标；(3)若点M 在第一象限内二次函数图象上，是否存在以CD 为直角边的Rt MCD ，若存在，求出点M 的坐标，若不存在，请说明理由．13．如图，抛物线23y ax bx =+-与x 轴交于()2,0A -，()6,0B 两点，与y 轴交于点C ．直线l 与抛物线交于A ，D 两点，与y 轴交于点E ，点D 的坐标为()4,3-．(1)求抛物线的解析式；(2)若点P 是抛物线上的点，点P 的横坐标为()0m m ≥，过点P 作PM x ⊥轴，垂足为M ．PM 与直线l 交于点N ，当点N 是线段PM 的三等分点时，求点P 的坐标；(3)若点Q 是y 轴上的点，且45ADQ ∠=︒，求点Q 的坐标．14．如图，抛物线23y ax bx =+-与x 轴交于()30A -,，()1,0B 两点，与y 轴交于点C ．(1)求该抛物线的解析式；(2)若点E 是线段AC 上一动点，过点E 的直线EF 平行于y 轴并交抛物线于点F ，当线段EF 取得最大值时，在x 轴上是否存在这样的点P ，使得以点E 、B 、P 为顶点的三角形是以EB 为腰的等腰三角形？若存在，请求出所有点P 的坐标；若不存在，请说明理由．15．如图，抛物线2y x bx c =-++与x 轴相交于A ，B 两点（点A 位于点B 的左侧），与y 轴相交于点C ，M 是抛物线的顶点，直线1x =是抛物线的对称轴，且点C 的坐标为(0,3)．(1)求抛物线的解析式；(2)已知P 为线段MB 上一个动点，过点P 作PD x ⊥轴于点D ．若,PD m PCD =△的面积为S ．⊥求S 与m 之间的函数关系式，并写出自变量m 的取值范围；⊥当S 取得最大值时，求点P 的坐标．(3)在（2）的条件下，在线段MB 上是否存在点P ，使PCD 为等腰三角形？如果存在，直接写出满足条件的点P 的坐标；如果不存在，请说明理由．16．如图，在平面直角坐标系中，已知抛物线y =ax 2+4x +c 与直线AB 相交于点A (0，1)和点B (3，4)．(1)求该抛物线的解析式；(2)设C 为直线AB 上方的抛物线上一点，连接AC ，BC ，以AC ，BC 为邻边作平行四边形ACBP ，求四边形ACBP 面积的最大值；(3)将该抛物线向左平移2个单位长度得到抛物线y =a 1x 2+b 1x +c 1（a 1≠0），平移后的抛物线与原抛物线相交于点D ，是否存在点E 使得△ADE 是以AD 为腰的等腰直角三角形？若存在，直接写出．．．．点E 的坐标；若不存在，请说明理由．17．如图，在平面直角坐标系中，抛物线223y x x =--与x 轴相交于点A 、B （点A 在点B 的左侧），与y 轴相交于点C ，连接,AC BC ．(1)求线段AC 的长；(2)若点Р为该抛物线对称轴上的一个动点，当PA PC =时，求点P 的坐标；(3)若点M 为该抛物线上的一个动点，当BCM 为直角三角形时，求点M 的坐标．18．如图，已知抛物线212y x bx c =++经过点B （4，0）和点C （0，－2），与x 轴的另一个交点为点A ，其对称轴l 与x 轴交于点E ，过点C 且平行x 轴的直线交抛物线于点D ，连接AD ．(1)求该抛物线的解析式；(2)判断⊥ABD 的形状，并说明理由；(3)P 为线段AD 上一点，连接PE ，若△APE 是直角三角形，求点P 的坐标；(4)抛物线的对称轴上是否存在一点P ，使△APD 是直角三角形，若存在，求出P 点坐标；若不存在，请说明理由．19．如图，抛物线22y ax x c =-+与x 轴相交于A ，B 两点，与y 轴相交于点C ，点A 在点B 的左侧，()1,0A -，()0,3C -，点E 是抛物线的顶点，P 是抛物线对称轴上的点．(1)求抛物线的函数表达式；(2)当点P 关于直线BC 的对称点Q 落在抛物线上时，求点Q 的横坐标；(3)若点D 是抛物线上的动点，是否存在以点B ，C ，P ，D 为顶点的四边形是平行四边形．若存在，直接写出点D 的坐标__________；若不存在，请说明理由；(4)直线CE 交x 轴于点F ，若点G 是线段EF 上的一个动点，是否存在以点O ，F ，G 为顶点的三角形与ABC 相似，若存在，请直接写出点G 的坐标__________；若不存在，请说明理由．20．如图1，抛物线23y ax bx =++与x 轴交于点()3,0A 、()1,0B -，与y 轴交于点C ，点P 为x 轴上方抛物线上的动点，点F 为y 轴上的动点，连接PA ，PF ，AF ．(1)求该抛物线所对应的函数解析式；(2)如图1，当点F 的坐标为()0,4-，求出此时AFP 面积的最大值；(3)如图2，是否存在点F ，使得AFP 是以AP 为腰的等腰直角三角形？若存在，求出所有点F 的坐标；若不存在，请说明理由．参考答案：1．(1)213222y x x =-++ (2)存在，Q (3，2)或Q (-1，0)(3)两个“和谐点”，1A 的横坐标是1或122．(1)222433y x x =-++ (2)22655PN m m =-+ (3)存在，741253．(1)24y x x =-+(2)3(3)（2，0）或（﹣4，0）或（﹣2，0）或（4，0）．4．(1)y =-x 2+4x (2)94(3)存在，点P 的坐标为(3+或(3-或（5，-5）或（4，0）5．(1)2142y x x =+- (2)（-2，-4）(3)P 点坐标为：（-1，3），（-1，-5），(12--+，，(12--， 6．(1)21262y x x =-++ (2)()2,2(3)()4,2或(27．(1)2y x 2x 3=-++(2)见解析(3)存在，2或28．(1)234y x x =--+(2)(1,6)D -或(3,4)D -(3)()3,4-或(0,4)或2⎫⎪⎪⎝⎭或2⎫⎪⎪⎝⎭9．(1)211342y x x =-++(2)1(3)()2,1-，()32，(12--10．(1)y ＝-x 2-2x ＋3，B (1，0)(2)存在，D (－2，3) (3)D (－52，74)或(－4，－5)11．(1)y ＝2x 2+3x ﹣1(2)t 2+2(3)t ＝012．(1)2+23y x x =-+(2)P 1（32，154），P 2（2，3）(3)存在点M 其坐标为1M 43539（，）或2M13．(1)y ＝14x 2−x −3 (2)（3，−154）或（0，−3） (3)（0，−133）或（0，9）14．(1)223y x x =+-(2)()4,-0，或10⎛⎫ ⎪ ⎪⎝⎭，或10⎛⎫ ⎪ ⎪⎝⎭15．(1)2y x 2x 3=-++ (2)⊥213(04)42S m m m =-+<≤；⊥S 有最大值为94，此时3,32P ⎛⎫ ⎪⎝⎭(3)存在，(6-+-或(42-+16．(1)241y x x =-++ (2)274(3)存在，E （4，3）或（-2，5）或（-3，2）或（3，0）．17．(2)()11，-(3)()14-，或()25-，或⎝⎭或⎝⎭18．(1)213222y x x =-- (2)直角三角形，见解析(3)(1，－1)或(32，－54)(4)存在，( 32，－1＋2 )，( 32，－1－ 2，( 32，5)，( 32，－5) 19．(1)223y x x =-- (2)11(3)存在，()2,3-或()4,5或()2,5-(4)存在，39,44⎛⎫-- ⎪⎝⎭或()1,2--20．(1)2y x 2x 3=-++ (2)323(3)存在，12(0,3),(0,1)F F --，32)F。

专题22.1 二次函数的图像和性质知识点解读 1.定义一般地，如果c b a c bx ax y ,,(2++=是常数，)0≠a ，那么y 叫做x 的二次函数。

其中x 是自变量，a 、b 、c 分别是函数解析式的二次项系数、一次项系数、常数项。

2.抛物线的三要素：开口方向、对称轴、顶点。

①a 的符号决定抛物线的开口方向：当0>a 时，开口向上；当0<a 时，开口向下；a 相等，抛物线的开口大小、形状相同。

②平行于y 轴（或重合）的直线记作h x =.特别地，y 轴记作直线0=x 。

3.几种特殊的二次函数的图像特征如下4.求抛物线的顶点、对称轴的方法①公式法：a b ac a b x a c bx ax y 442222-+⎪⎭⎫ ⎝⎛+=++=， ∴顶点是），（ab ac a b 4422--，对称轴是直线abx 2-=。

②配方法：运用配方的方法，将抛物线的解析式化为()k h x a y +-=2的形式，得到顶点为(h ,k )，对称轴是直线h x =。

③运用抛物线的对称性：由于抛物线是以对称轴为轴的轴对称图形，对称轴与抛物线的交点是顶点。

若已知抛物线上两点12(,)(,)、x y x y （及y 值相同），则对称轴方程可以表示为：122x x x +=5.抛物线c bx ax y ++=2中， a 、b 、c 的作用①a 决定开口方向及开口大小，这与2ax y =中的a 完全一样。

②b 和a 共同决定抛物线对称轴的位置.由于抛物线c bx ax y ++=2的对称轴是直线abx 2-=，故：①0=b 时，对称轴为y 轴；②0>a b （即a 、b 同号）时，对称轴在y 轴左侧；③0<ab（即a 、b 异号）时，对称轴在y 轴右侧。

③c 的大小决定抛物线c bx ax y ++=2与y 轴交点的位置。

当0=x 时，c y =，∴抛物线c bx ax y ++=2与y 轴有且只有一个交点（0，c ）： ①0=c ，抛物线经过原点; ②0>c ,与y 轴交于正半轴； ③0<c ,与y 轴交于负半轴.以上三点中，当结论和条件互换时，仍成立.如抛物线的对称轴在y 轴右侧，则 0<ab6.用待定系数法求二次函数的解析式一般情况下设二次函数的解析式为y=ax 2+bx+c ，结合题中条件解出a 、b 、c 就可以求出二次函数的解析式。

第5讲二次函数的图象与性质知识定位讲解用时：2分钟A、适用范围：人教版初三，基础一般B、知识点概述：本讲义主要用于人教版初三新课，本节课我们主要学习二次函数的图象与性质，本节课的重点是掌握二次函数的平移法则，能够结合二次函数图象和性质判断a、b、c的之间的关系，而难点在于二次函数的图象和性质的综合考查，需要学生能够根据二次函数的图象与性质正确分析并解决问题。

希望同学们能够认真学习并掌握，为后面二次函数的应用打好基础。

知识梳理讲解用时：25分钟二次函数的图象（1）二次函数y=ax2（a≠0）的图象的画法：①列表：先取原点（0，0），然后以原点为中心对称地选取x值，求出函数值，列表；①描点：在平面直角坐标系中描出表中的各点；①连线：用平滑的曲线按顺序连接各点；①在画抛物线时，取的点越密集，描出的图象就越精确，但取点多计算量就大，故一般在顶点的两侧各取三四个点即可，连线成图象时，要按自变量从小到大（或从大到小）的顺序用平滑的曲线连接起来，画抛物线y=ax2（a≠0）的图象时，还可以根据它的对称性，先用描点法描出抛物线的一侧，再利用对称性画另一侧。

x…-223--112-0121232…2y x= (4)491140141494…（2）二次函数y=ax2+bx+c（a≠0）的图象二次函数y=ax2+bx+c（a≠0）的图象看作由二次函数y=ax2的图象向右或向左平移|ab2|个单位，再向上或向下平移|abac442-|个单位得到的。

12341234xyxyOO1212----图1图2向上（）或向下（）平移个单位向上（）或向下（）平移个单位向左（）或向右（）平移个单位向左（）或向右（）平移个单位课堂精讲精练【例题1】抛物线212y x =向左平移8个单位，再向下平移9个单位，所得的抛物线的解析式是___________________。

【答案】218232y x x =++【解析】本题考查了二次函数平移规则，根据二次函数的平移法则，“上加下减，左加右减”，可知平移后的函数解析式为()21892y x =+-，整理即为218232y x x =++讲解用时：2分钟解题思路：牢记平移法则即可。