信号与通信系统-第一次习题课

习 题 一 第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD （15,6）=3 Hz 。

因此，公共周期3110==f T s 。

(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD （5, 15）=5 Hz 。

因此，公共周期5110==f T s 。

(c) 由于两个分量的频率1ω=10π rad/s 、1ω=20 rad/s 的比值是无理数，因此无法找出公共周期。

所以是非周期的。

(d) 两个分量是同频率的，基频 =0f 1/π Hz 。

因此，公共周期π==01f T s 。

1-2 解 (a) 波形如图1-2(a)所示。

显然是功率信号。

t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。

显然是能量信号。

3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号，显然有 1=P W1-3 解 周期T=7 ，一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+； (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。

1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。

1试分别指出以下波形是属于哪种信号？题图1-11-2试写出题1-1图中信号的函数表达式。

1-3已知信号)(1t x 与)(2t x 波形如题图1-3中所示，试作出下列各信号的波形图，并加以标注。

题图1-3⑴)2(1-t x ⑵)1(1t x -⑶)22(1+t x⑷)3(2+t x ⑸)22(2-t x ⑹)21(2t x - ⑺)(1t x )(2t x -⑻)1(1t x -)1(2-t x ⑼)22(1t x -)4(2+t x 1-4已知信号)(1n x 与)(2n x 波形如题图1-4中所示，试作出下列各信号的波形图，并加以标注。

题图1-4⑴)12(1+n x ⑵)4(1n x -⑶)2(1n x ⑷)2(2n x -⑸)2(2+n x ⑹)1()2(22--++n x n x⑺)2(1+n x )21(2n x -⑻)1(1n x -)4(2+n x ⑼)1(1-n x )3(2-n x1-5已知信号)25(t x -的波形如题图1-5所示，试作出信号)(t x 的波形图，并加以标注。

题图1-51-6试画出下列信号的波形图：⑴)8sin()sin()(t t t x ΩΩ=⑵)8sin()]sin(211[)(t t t x ΩΩ+= ⑶)8sin()]sin(1[)(t t t x ΩΩ+=⑷)2sin(1)(t tt x = 1-7试画出下列信号的波形图：⑴)(1)(t u e t x t -+=⑵)]2()1([10cos )(---=-t u t u t e t x t π⑶)()2()(t u e t x t --=⑷)()()1(t u e t x t --=⑸)9()(2-=t u t x ⑹)4()(2-=t t x δ1-8试求出以下复变函数的模与幅角，并画出模与幅角的波形图。

⑴)1(1)(2Ω-Ω=Ωj e j X ⑵)(1)(Ω-Ω-Ω=Ωj j e e j X ⑶Ω-Ω---=Ωj j e e j X 11)(4⑷21)(+Ω=Ωj j X 1-9已知信号)]()([sin )(π--=t u t u t t x ，求出下列信号，并画出它们的波形图。

第1章 习题答案1－1 题1－1图所示信号中，哪些是连续信号？哪些是离散信号？哪些是周期信号？哪些是非周期信号？哪些是有始信号？解： ① 连续信号：图（a ）、（c ）、（d ）； ② 离散信号：图（b ）； ③ 周期信号：图（d ）；④ 非周期信号：图（a ）、（b ）、（c ）； ⑤有始信号：图（a ）、（b ）、（c ）。

1－2 已知某系统的输入f(t)与输出y(t)的关系为y(t)=|f(t)|，试判定该系统是否为线性时不变系统。

解： 设T 为此系统的运算子，由已知条件可知： y(t)=T[f(t)]=|f(t)|，以下分别判定此系统的线性和时不变性。

① 线性1）可加性不失一般性，设f(t)=f 1(t)+f 2(t)，则y 1(t)=T[f 1(t)]=|f 1(t)|，y 2(t)=T[f 2(t)]=|f 2(t)|，y(t)=T[f(t)]=T[f 1(t)+f 2(t)]=|f 1(t)+f 2(t)|，而|f 1(t)|＋|f 2(t)|≠|f 1(t)+f 2(t)|即在f 1(t)→y 1(t)、f 2(t)→y 2(t)前提下，不存在f 1(t)＋f 2(t)→y 1(t)＋y 2(t)，因此系统不具备可加性。

由此，即足以判定此系统为一非线性系统，而不需在判定系统是否具备齐次性特性。

2）齐次性由已知条件，y(t)=T[f(t)]=|f(t)|，则T[af(t)]=|af(t)|≠a|f(t)|=ay(t) （其中a 为任一常数）即在f(t)→y(t)前提下，不存在af(t)→ay(t),此系统不具备齐次性，由此亦可判定此系统为一非线性系统。

② 时不变特性由已知条件y(t)=T[f(t)]=|f(t)|，则y(t-t 0)=T[f(t-t 0)]=|f(t-t 0)|，即由f(t)→y(t)，可推出f(t-t 0)→y(t-t 0)，因此，此系统具备时不变特性。

依据上述①、②两点，可判定此系统为一非线性时不变系统。

通信原理教程课后练习题含答案第一部分：选项题（单选题）1.在通信系统中，为什么需要抗噪性能？A. 防止信号失真B. 提高当前信号的频率C. 压缩信道的频带宽度D. 抵抗信号的干扰和噪声答案：D解析：在通信系统中，我们需要考虑信号的传输过程，不仅需要传送正确的信息，还需要保证传送过程中的信号质量，抗噪性能就是指在传送过程中，系统能够抵御外部干扰和噪声等不利因素对信号的影响。

2.以下哪个是数字信号的优点？A. 抗噪性强B. 信号质量稳定C. 低成本D. 传输距离远答案：A解析：数字信号可以被编码和解码，可以进行纠错和压缩，通过数字信号处理技术可以消除大部分噪音和失真，因此数字信号的抗噪性能相比于模拟信号更加优异。

3.以下哪些是同步通讯的技术？A. 分组交换B. 时隙复用C. 频分复用D. 波分复用答案：B解析：同步通讯是指，在通信系统中，发送方与接收方在时间上保持同步。

其中时隙复用技术就是同步通讯的一种方法，该方法把时间分为若干个时隙，发送方和接收方在同样的时隙内进行传输和接收数据。

第二部分：填空题（构造题）1.在FSK调制中，当载波波形为正弦波时，可得到_____频带宽度，但是两种不同的调制信号之间在频谱上无法有效分离。

答案：相同解析：FSK调制中，载波的频率被两个离散的数字调制信号所取代，当载波波形为正弦波时，可得到相同频带宽度，但是两种不同的调制信号之间在频谱上无法有效分离。

2.在AM调制中，存在一个_____问题导致了它的不稳定性，这个问题通过使用_____调制技术得到了解决。

答案：抑制振荡；DSB-SC解析：AM调制中存在一个抑制振荡的问题，它导致了AM信号的不稳定性和失真，为了解决这个问题，可以使用DSB-SC调制技术，该技术在调制信号之前，在载波上进行一定程度的频偏，可以有效的避免抑制振荡。

第三部分：应用题（综合题）1.一个数据通道的带宽是100KHz，数据率是10Mbps。

为了能够满足该数据通道的传输要求，需要采用什么调制方式？答案：QAM解析：QAM调制是一种有限带宽调制，它将数据信号分为I和Q两路，通过I 路和Q路的幅度和相位来调制载波信号，因此它可以实现更高的数据速率和更小的频带占用率。

第一次作业见网络课件各章练习题（课件中个别题目有误，以以下题目为准）。

网络课件中的题目为典型性题目，希望大家都能做一遍，以下题目为必做题，要上交。

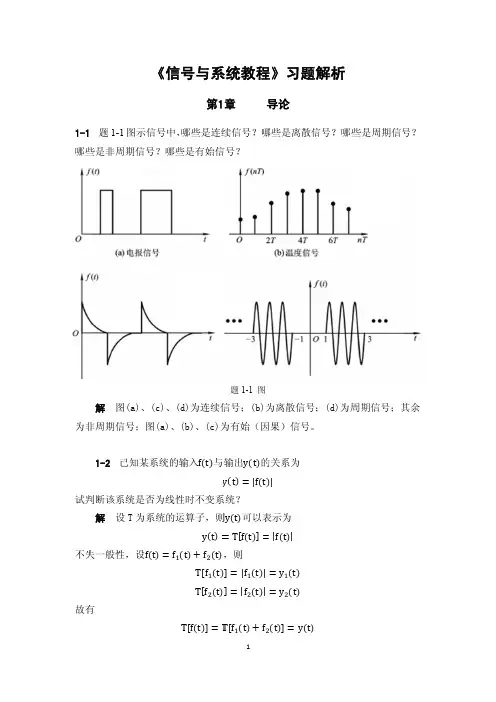
第一章2、3、5、62．请画出数字通信系统的基本原理方框图，并说明各个环节的作用。

答：源与信宿：信源是将消息转换为电信号；信宿则是将电信号还原为原始消息。

信源编码和信源解码：信源编码对模拟信源作用有二：模/数转换和码率压缩；对数字信源来说，进行码率压缩来提高传输效率。

信源解码是信源编码的逆过程。

信道编码和信道解码：信道编码是为提高系统的可靠性，达到纠错和检错的目的而按照一定规律进行的编码过程；信道解码是信道编码的逆过程。

调制和解调：数字调制的任务就是把数字基带信号转换成适于信道传输的数字已调信号；数字解调是数字调制的逆过程。

信道：是信号传输的媒介。

噪声源－为了方便分析，人们通常把始端、终端与传输信道中所存在的干扰都折合到信道中，等效为一个总的噪声源。

3．衡量数字通信系统的主要性能指标是什么？答：有效性可用传输速率来衡量。

系统的可靠性具体可用差错率来衡量传输速率1 码元传输速率码元传输速率，又称为码元速率或传码率。

其定义为每秒钟传送码元的数目，单位为"波特",常用符号"B"表示。

2 信息传输速率传输速率还可用信息传输速率来表征。

信息传输速率又称为信息速率和传信率。

通常定义每秒钟传递的信息量为传信率，单位是比特/秒(bit/s或bps)。

差错率差错率是衡量系统正常工作时，传输消息可靠程度的重要性能指标。

差错率有两种表述方法:1.误码率: 是指错误接收的码元数在传送总码元数中所占的比例，或者更确切地说，误码率是码元在传输系统中被传错的概率。

2.误信率:又称误比特率，是指错误接收的信息量在传送信息总量中所占的比例，或者说，它是码元的信息量在传输系统中被丢失的概率。

5．设有四个消息符号，其前三个符号出现概率分别是1/4，1/8，1/8。

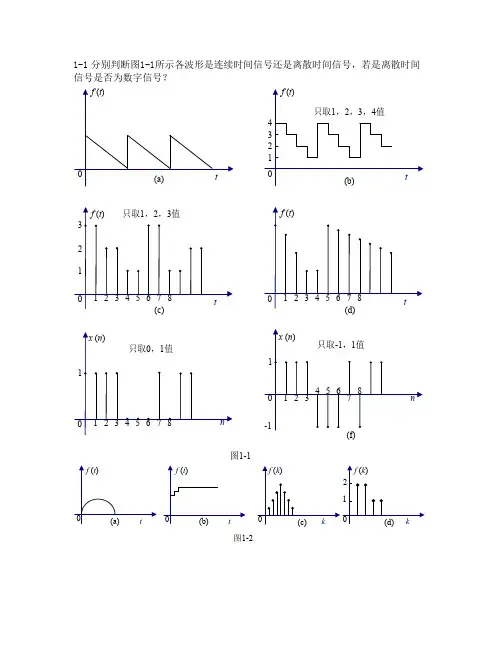
1-1分别判断图1-1所示各波形是连续时间信号还是离散时间信号，若是离散时间信号是否为数字信号？图1-1图1-2解 信号分类如下：图1-1所示信号分别为⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧--⎩⎨⎧--））（散（例见图数字：幅值、时间均离））（连续（例见图抽样：时间离散，幅值离散））（连续（例见图量化：幅值离散，时间））（续（例见图模拟：幅值、时间均连连续信号d 21c 21b 21a 21（a ）连续信号（模拟信号）；（b ）连续（量化）信号；（c ）离散信号，数字信号；（d ）离散信号；（e ）离散信号，数字信号；（f ）离散信号，数字信号。

1-2 分别判断下列各函数式属于何种信号？（重复1-1题所示问）（1）；)sin(t e at ω-（2）；nT e -（3）；)cos(πn （4）；为任意值）（00)sin(ωωn （5）。

221⎪⎭⎫ ⎝⎛解由1-1题的分析可知：（1）连续信号；（2）离散信号；（3）离散信号，数字信号；（4）离散信号；（5）离散信号。

1-3 分别求下列各周期信号的周期T ：（1）；)30t (cos )10t (cos -（2）；j10t e （3）；2)]8t (5sin [（4）。

[]为整数）（n )T nT t (u )nT t (u )1(0n n ∑∞=-----解 判断一个包含有多个不同频率分量的复合信号是否为一个周期信号，需要考察各分量信号的周期是否存在公倍数，若存在，则该复合信号的周期极为此公倍数；若不存在，则该复合信号为非周期信号。

（1）对于分量cos (10t )其周期；对于分量cos (30t )，其周期。

由于5T 1π=15T 2π=为的最小公倍数，所以此信号的周期。

5π21T T 、5T π=（2）由欧拉公式)t (jsin )t (cos e t j ωωω+=即)10t (jsin )10t (cos e j10t +=得周期。

5102T ππ==（3）因为[])16t (cos 2252252)16t (cos 125)8t (5sin 2-=-⨯=所以周期。

1-4 分析过程：（1）例1-1的方法：()()()()23232f t f t f t f t →−→−→−− （2）方法二：()()()233323f t f t f t f t ⎡⎤⎛⎞→→−→−−⎜⎟⎢⎥⎝⎠⎣⎦（3）方法三：()()()()232f t f t f t f t →−→−+→−−⎡⎤⎣⎦ 解题过程：（1）方法一：方法二：（1）()−f at 左移0t ：()()()000−+=−−≠−⎡⎤⎣⎦f a t t f at at f t at （2）()f at 右移0t ：()()()000−=−≠−⎡⎤⎣⎦f a t t f at at f t at （3）()f at 左移0t a ：()()000⎡⎤⎛⎞+=+≠−⎜⎟⎢⎥⎝⎠⎣⎦t f a t f at t f t at a （4）()f at 右移0t a ：()()000⎡⎤⎛⎞−−=−+=−⎜⎟⎢⎥⎝⎠⎣⎦t f a t f at t f t at a 故（4）运算可以得到正确结果。

注：1-4、1-5题考察信号时域运算：1-4题说明采用不同的运算次序可以得到一致的结果；1-5题提醒所有的运算是针对自变量t 进行的。

如果先进行尺度变换或者反转变换，再进行移位变换，一定要注意移位量和移位的方向。

1-9 解题过程： （1）()()()2tf t eu t −=− （2）()()()232tt f t ee u t −−=+（3）()()()255ttf t e eu t −−=− （4）()()()()cos 1012tf t et u t u t π−=−−−⎡⎤⎣⎦1-12 解题过程：（（（（注：1-9、1-12题中的时域信号均为实因果信号，即()()()=f t f t u t 1-18 分析过程：任何信号均可分解为奇分量与偶分量之和的形式，即()()()()1e o f t f t f t =+其中，()e f t 为偶分量，()o f t 为奇分量，二者性质如下：()()()()()()23e e o o f t f t f t f t =−=−−()()13∼式联立得()()()12e f t f t f t =+−⎡⎤⎣⎦ ()()()12o f t f t f t =−−⎡⎤⎣⎦ 解题过程：(a-1) (a-2)(a-3)(a-4)f t为偶函数，故只有偶分量，为其本身(b) ()(c-1)(c-2)(c-3)(c-4)(d-1)(d-2)(d-3)(d-4)1-20 分析过程：本题为判断系统性质：线性、时不变性、因果性（1）线性（Linearity）：基本含义为叠加性和均匀性即输入()1x t ，()2x t 得到的输出分别为()1y t ，()2y t ，()()11T x t y t =⎡⎤⎣⎦，()()22T x t y t =⎡⎤⎣⎦，则()()()()11221122T c x t c x t c y t c y t +=+⎡⎤⎣⎦（1c ，2c 为常数）。

第一章 习 题1-1 画出下列各信号的波形：(1) f 1(t)=(2-e -t )U(t); (2) f 2(t)=e -t cos10πt×[U(t -1)-U(t-2)]。

答案（1）)(1t f 的波形如图1.1（a ）所示.(2) 因t π10cos 的周期s T 2.0102==ππ,故)(2t f 的波形如图题1.1(b)所示.1-2 已知各信号的波形如图题1-2所示，试写出它们各自的函数式。

答案)1()]1()([)(1-+--=t u t u t u t t f)]1()()[1()(2----=t u t u t t f)]3()2()[2()(3----=t u t u t t f1-3 写出图题1-3所示各信号的函数表达式。

答案2002121)2(21121)2(21)(1≤≤≤≤-⎪⎩⎪⎨⎧+-=+-+=+=t t t t t t t f)2()1()()(2--+=t u t u t u t f)]2()2([2sin )(3--+-=t u t u t t f π)3(2)2(4)1(3)1(2)2()(4-+---++-+=t u t u t u t u t u t f1-4 画出下列各信号的波形：(1) f 1(t)=U(t 2-1); (2) f 2(t)=(t-1)U(t 2-1);(3) f 3(t)=U(t 2-5t+6); (4)f 4(t)=U(sinπt)。

答案(1) )1()1()(1--+-=t u t u t f ,其波形如图题1.4(a)所示.(2))1()1()1()1()]1()1()[1()(2---+--=--+--=t u t t u t t u t u t t f 其波形如图题1.4(b)所示.(3))3()2()(3-++-=t u t u t f ,其波形如图1.4(c)所示.(4) )(sin )(4t u t f π=的波形如图题1.4(d)所示.1-5 判断下列各信号是否为周期信号，若是周期信号，求其周期T 。

习题课（from 1~7）第四章 信道4-6某个信源由A 、B 、C 和D 4个符号组成。

设每个符号独立出现，其出现概率分别为1/4、1/4、3/16、5/16，经过信道传输后，每个符号正确接收的概率为1021/1024，错为其它符号的条件概率(/)i j P x y 均为1/1024，试求出该信道的容量C 。

解：根据离散信道信道容量的定义，()max[()(|)]p x C H X H X Y =-。

即，以()p x 为变量，取()(|)H X H X Y -的最大值。

4441114441111(|)()(|)()(|)log(|)1102110241()(|)log ()[log 3*log1024](|)102410211024102110241[log 3*log1024]*10.0335/102410211024j j j i j j j i i j j i j j j i j i j H X Y p y H X y p y p x y p x y p y p x y p y p x y bit symbol ==========+=+=∑∑∑∑∑∑ (1) 通过上述计算发现，对题中所给的对称信道，(|)H X Y 是一个常数，与()p x 无关。

因此，最大化()(|)H X H X Y -简化为最大化()H X 。

根据题意，X 有4种可能，因此()2/H X bit symbol ≤，则()max[()(|)]20.0335 1.9665/p x C H X H X Y bit symbol =-=-=(2)@知识点：离散信道信道容量的定义。

在离散对称信道下，通过计算可知(|)H X Y 是与输入无关的常数。

这使得信道容量的计算得到简化。

@注意：题中的概率值(/)i j P x y ，不是信道转移概率，而是后验概率。

信道转移概率定义为(/)j i P y x ，计算需要严格按照信道容量的定义()max [()(|)]p y C H Y H Y X =-进行，这时需要搜索C 最大时对应的概率值。