下载文档原格式
第九章 刚体的平面运动一、判断题1．刚体作平面运动时，绕基点转动的角速度和角加速度与基点的选取无关。
（ ） 答案：√2．作平面运动的刚体相对于不同基点的平动坐标系有相同的角速度与角加速度。
（ ） 答案：√3．刚体作平面运动时，平面图形内两点的速度在任意轴上的投影相等。
（ ） 答案：×4．某刚体作平面运动时，若A 和B 是其平面图形上的任意两点，则速度投影定理AB B AB A u u ][][=永远成立。
（ ）答案：√5．刚体作平面运动，若某瞬时其平面图形上有两点的加速度的大小和方向均相同，则该瞬时此刚体上各点的加速度都相同。
（ ）答案：√6．圆轮沿直线轨道作纯滚动，只要轮心作匀速运动，则轮缘上任意一点的加速度的方向均指向轮心。
（ ）答案：√二、选择题1．杆AB 的两端可分别沿水平、铅直滑道运动，已知B 端的速度为B u，则图示瞬时B点相对于A 点的速度为 。
A vB sin θ； B v B cos θ；C v B /sin θ；D v B /cos θ。
答案：D2．在图示内啮合行星齿轮转动系中，齿轮Ⅱ固定不动。
已知齿轮Ⅰ和Ⅱ的半径各为r 1和r 2，曲柄OA 以匀角速度ω0逆时针转动，则齿轮Ⅰ对曲柄OA 的相对角速度ω1r 应为 。
A ω1r =（r 2/ r 1）ω0（逆钟向）；B ω1r =（r 2/ r 1）ω0（顺钟向）；C ω1r =[(r 2+ r 1)/ r 1] ω0（逆钟向）；D ω1r =[(r 2+ r 1)/ r 1] ω0（顺钟向）。
答案：B3．一正方形平面图形在其自身平面内运动，若其顶点A 、B 、C 、D 的速度方向如图（a ）、图（b ）所示，则图（a ）的运动是 的，图（b ）的运动是 的。
A 可能；B 不可能；C 不确定。
答案：B A三、填空题1．指出图示机构中各构件作何种运动，轮A （只滚不滑）作 ；杆BC 作 ；杆CD 作 ；杆DE 作 。
第九章 刚体的平面运动1、 基本要求（1） 熟练掌握基点法、速度瞬心法求解平面运动刚体的速度；（2） 熟练掌握基点法求解平面运动刚体的加速度；（3） 熟练应用点的复合运动和刚体的平面运动定理求解刚体系中各构件的速度和加速度。
注：牵连运动只要求掌握平移和定轴转动两种，牵连运动为平面运动超大纲，不要求。
2、 知识点（1） 平面运动的分解：（要真正理解并运用）可取任意基点将平面运动分解为平移和转动，其中平移的速度和加速度与基点的选择有关，而平面图形绕基点转动的角速度和角加速度与基点的选择无关。
（2） 求平面运动刚体的速度：三种方法✧ 基点法：平面图形内任一点B 的速度等于基点A 的速度与该点随图形绕基点转动速度的矢量和。
B A BA v v v =+其中，BA v AB ω=⋅，方向垂直于AB ，朝向图形转动的一方。
基点A 的选取原则：其运动速度大小与方向已知。
✧ 速度投影定理()()B A AB AB v v =同一平面图形上任意两点的速度在这两点连线上的投影相等。
✧ 速度瞬心法● 刚体作平面运动时，每瞬时都有且仅有一个速度瞬心；● 在不同瞬时，速度瞬心点的位置不同；● 平面图形的平面运动可看作绕速度瞬心P 的瞬时转动。
（对速度而言） 注意：并非真正绕速度瞬心作定轴转动，因0P a ≠。
● 四类速度瞬时如何确定参见第九章PPT2。
✧ 三种方法比较：● 速度投影定理无法求出刚体转动的角速度，而在求加速度时又要用到此参量，故通常不用速度投影定理来求解速度与角速度。
通常该定理主要用于判定点的速度的确切指向。
● 首选速度瞬心法：前提必须知道刚体上任意两点的速度方向。
● 基点法：在以下两种情况下只能用基点法：(a) 只知道刚体上某一点的速度大小与方向，其它各点大小方向均未知；(b) 速度瞬心虽可找到但几何关系过于复杂。
（3） 求平面运动刚体的加速度：唯一的方法 —— 基点法平面图形内任一点的加速度等于基点的加速度与该点随图形绕基点转动的切向加速度和法向加速度的矢量和。
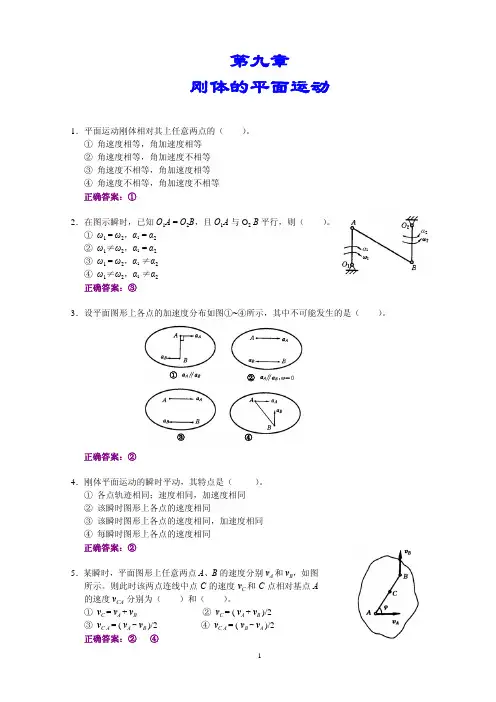
第九章刚体的平面运动1．平面运动刚体相对其上任意两点的（ ）。
① 角速度相等，角加速度相等② 角速度相等，角加速度不相等③ 角速度不相等，角加速度相等④ 角速度不相等，角加速度不相等正确答案：①2．在图示瞬时，已知O 1A = O 2B ，且O 1A 与O 2 B 平行，则（ ）。
① ω1 = ω2，α1 = α2② ω1≠ω2，α1 = α2③ ω1 = ω2，α1 ≠α2④ ω1≠ω2，α1 ≠α2正确答案：③3．设平面图形上各点的加速度分布如图①~④所示，其中不可能发生的是（ ）。
正确答案：②4．刚体平面运动的瞬时平动，其特点是（ ）。
① 各点轨迹相同；速度相同，加速度相同② 该瞬时图形上各点的速度相同③ 该瞬时图形上各点的速度相同，加速度相同④ 每瞬时图形上各点的速度相同正确答案：②5．某瞬时，平面图形上任意两点A 、B 的速度分别v A 和v B ，如图所示。
则此时该两点连线中点C 的速度v C 和C 点相对基点A的速度v CA 分别为（ ）和（ ）。
① v C = v A + v B ② v C = ( v A + v B )/2③ v C A = ( v A - v B )/2 ④ v C A = ( v B - v A )/2正确答案：② ④α1α2 ①②③④6．平面图形上任意两点A 、B 的加速度a A 、a B 与连线AB 垂直，且a A ≠ a B ，则该瞬时，平面图形的角速度ω和角加速度α应为（ ）。
① ω≠0，α ≠0② ω≠0，α = 0③ ω = 0，α ≠0④ ω = 0，α = 0正确答案：③7．平面机构在图示位置时，AB 杆水平，OA 杆鉛直。
若B 点的速度v B ≠0，加速度τB a = 0，则此瞬时OA 杆的角速度ω和角加速度α为（ ）。
① ω = 0，α ≠0② ω≠0，α = 0③ ω = 0，α = 0④ ω≠0，α ≠0正确答案：②8．在图示三种运动情况下，平面运动刚体的速度瞬心：（a ）为（ ）；（b ）为（ ）；（c ）为（ ）。
第九章 刚体的平面运动
9-1 椭圆规尺AB 由曲柄OC
带动，曲柄以角速度O ω绕O
轴匀速转动，如图所示。
如
OC=BC=AC=r ，并取C 为基
点，求椭圆规尺AB 的平面运
动方程。
9-2 如图所示，圆柱A 绕以细绳，绳的B 端固定在天花板上。
圆柱自静止落下，其轴心的速度为gh v 33
2=，其中g 为常量，h 为圆柱轴心到初始位置的距离。
如圆柱半径为r ，求圆柱的平面运动
方程。
9-3 半径为r 的齿轮由曲柄OA 带动，沿半径为R 的固定齿轮滚动，
如图所示。
如曲柄OA 以等角加速度ε绕O 轴转动，当运动开始时，
角速度0=O ω，转角0=ϕ。
求动齿轮以中心A 为基点的平面运
动方程。
9-4 如图所示，在筛动机构中，筛子的摆动是由曲柄连杆机构所带动。
已知曲柄OA 的转速min r 40=OA n ，OA =0.3m 。
当筛子BC 运动到与点O 在同一水平线上时，︒=∠90BAO 。
求此瞬时筛子BC 的速度。
9-5 图示两齿条以速度1v 和2v 同方向运动。
在两齿条间夹一齿轮，其半径为r ，求齿轮的角速度及其中心O 的速度。
9-6 四连杆机构中，连杆AB 上固连一块三角板ABD ，如图所示。
机构由曲柄O 1A 带动。
已知：曲柄的角速度s rad 21=A O ω；曲柄O 1A =0.1m ，水平距离O 1O 2=0.05m ， AD =0.05m ；当O 1A 铅直时，AB 平行于O 1O 2，且AD 与AO 1在同一直线上；
角︒=30ϕ。
求三角板ABD 的角速度和点D 的速度。
9-7图示机构中，已知：OA =0.1m ，BD =0.1m ，DE =0.1m ，
m 31.0=EF ；s rad 4=OA ω。
在图示位置时，曲柄OA 与
水平线OB 垂直；且B 、D 和F 在同一铅直线上。
又DE 垂直于
EF 。
求杆EF 的角速度和点F 的速度。
9-8 在瓦特行星传动机构中，平衡杆O 1A 绕O 1轴转动，并借连杆
AB 带动曲柄OB ；而曲柄OB 活动地装置在O 轴上，如图所示。
在O 轴上装有齿轮I ，齿轮II 与连杆AB 固连于一体。
已知：
m 33.021==r r ，O 1A =0.75m ，AB =1.5m ；又平衡杆的角速度
rad 61=O ω。
求当︒=60γ且︒=90β时，曲柄OB 和齿轮I
的角速度。
9-9 使砂轮高速转动的装置如图所示。
杆O 1O 2绕O 1轴转动，转速为n 4。
O 2处用铰链连接一半径为r 2的活动齿轮II ，杆O 1O 2转动时轮II 在半径为r 3的固定内齿轮III 上滚动，并使半径为r 1的轮I 绕O 1轴转动。
轮I 上装有砂轮，随同轮I 高速转动。
已知1113=r r ，m in r 9004=n ，求砂轮的转速。
9-10 图示小型精压机的传动机构，OA=O 1B=r =0.1m ， EB=BD=AD=l =0.4m 。
在图示瞬时，AD OA ⊥，ED B O ⊥1，O 1D 在水平位置，OD 和EF 在铅直位置。
已知曲柄OA 的转速m in r 120=n ，求此时压头F 的速度。
9-11 图示蒸汽机传动机构中，已知：活塞的速度为υ；
O 1A 1=a 1，O 2A 2=a 2，CB 1=b 1，CB 2=b 2；齿轮半径分别为
r 1和r 2；且有112221r b a r b a ≠。
当杆EC 水平，杆B 1B 2
铅直，A 1、A 2和O 1，O 2都在同一条铅直线上时，求齿
轮O 1的角速度。
9-12 半径为R 的轮子沿水平面滚动而不滑动，如图
所示。
在轮上有圆柱部分，其半径为r 。
将线绕于
圆柱上，线的B 端以速度v 和加速度a 沿水平方向
运动。
求轮的轴心O 的速度和加速度。
9-13 在图示曲柄连杆机构中，曲柄OA 绕O 轴转
动，其角速度为O ω，角加速度为O ε。
在某瞬时
曲柄与水平线间成︒60角，而连杆AB 与曲柄OA
垂直。
滑块B 在圆形槽内滑动，此时半径O 1B 与
连杆AB 间成︒30角。
如OA=r ，r AB 32=，
O 1B =2r ，求在该瞬时，滑块B 的切向和法向加速
度。
9-14 塔轮1半径为r =0.1m 和R =0.2m ，绕轴O 转动的规律是
rad 32t t -=ϕ，并通过不可伸长的绳子卷动动滑轮2，滑轮2的
半径为m 15.02=r 。
设绳子与各轮之间无相对滑动，求t =1s 时，
轮2的角速度和角加速度；并求该瞬时水平直径上C 、D 、E 各点的
速度和加速度。
9-15 图示直角刚性杆，AC=CB =0.5m ，
设在图示瞬时，两端滑块沿水平与铅垂轴
的加速度如图，大小分别为
2m 1=A a ，2s m 3=B a 。
求这时直
角杆的角速度和角加速度。
9-16 如图所示，轮O 在水平面上滚动而不滑动，轮心以匀速s m 2.0=O υ运动。
轮缘上固连销钉B ，此销钉在摇杆O 1A 的槽内滑动，并带动摇杆绕O 1轴转动。
已知：轮的半径R =0.5m ，在图示位置时，AO 1是轮的切线，摇杆与水平面间的交角为︒60。
求摇杆在该瞬时的
角速度和角加速度。
9-17 已知图示机构中滑块A 的速度为常值，s m 2.0=A υ，
AB =0.4m 。
求当AB=BC ，︒=30θ时杆CD 的速度和加速度。
9-18 图示行星齿轮传动机构中，曲柄OA 以匀角速度O ω绕O
轴转动，使与齿轮A 固结在一起的杆BD 运动。
杆BE 与BD
在点B 铰接，并且杆BE 在运动时始终通过固定铰支的套筒C 。
如定齿轮的半径为2r ，动齿轮半径为r ，且r AB 5=。
图示瞬时，曲柄OA 在铅直位置，BD 在水平位置，杆BE 与水平线间成角︒=45ϕ。
求此时杆BE 上与C 相重合一点的速度和加速度。
9-19 图示放大机构中，杆I 和II 分别以速度1υ和2υ沿箭头方向运动，其位移分别以x 和y 表示。
如杆II 与杆III 平行，其间距离为a ，求杆III 的速度和滑道Ⅳ的角速度。
9-20 半径R =0.2m 的两个相同的大环沿地面向相反方向无滑动地滚动，环心的速度为常数；m 1.0=A υ。
m 4.0=B υ。
当︒=∠30MAB 时，求套在这两个大环上的小环M 相对于每个大环的速度和加速度，以及小环M 的绝对速度和绝对加速度。
